LeetCode 134. 加油站(函数图像法 / 贪心)
题目:
链接:LeetCode 134. 加油站
难度:中等
在一条环路上有 n 个加油站,其中第 i 个加油站有汽油 gas[i] 升。
你有一辆油箱容量无限的的汽车,从第 i 个加油站开往第 i+1 个加油站需要消耗汽油 cost[i] 升。你从其中的一个加油站出发,开始时油箱为空。
给定两个整数数组 gas 和 cost ,如果你可以绕环路行驶一周,则返回出发时加油站的编号,否则返回 -1 。如果存在解,则 保证 它是 唯一 的。
示例 1:
输入: gas = [1,2,3,4,5], cost = [3,4,5,1,2]
输出: 3
解释:
从 3 号加油站(索引为 3 处)出发,可获得 4 升汽油。此时油箱有 = 0 + 4 = 4 升汽油
开往 4 号加油站,此时油箱有 4 - 1 + 5 = 8 升汽油
开往 0 号加油站,此时油箱有 8 - 2 + 1 = 7 升汽油
开往 1 号加油站,此时油箱有 7 - 3 + 2 = 6 升汽油
开往 2 号加油站,此时油箱有 6 - 4 + 3 = 5 升汽油
开往 3 号加油站,你需要消耗 5 升汽油,正好足够你返回到 3 号加油站。
因此,3 可为起始索引。
示例 2:
输入: gas = [2,3,4], cost = [3,4,3]
输出: -1
解释:
你不能从 0 号或 1 号加油站出发,因为没有足够的汽油可以让你行驶到下一个加油站。
我们从 2 号加油站出发,可以获得 4 升汽油。 此时油箱有 = 0 + 4 = 4 升汽油
开往 0 号加油站,此时油箱有 4 - 3 + 2 = 3 升汽油
开往 1 号加油站,此时油箱有 3 - 3 + 3 = 3 升汽油
你无法返回 2 号加油站,因为返程需要消耗 4 升汽油,但是你的油箱只有 3 升汽油。
因此,无论怎样,你都不可能绕环路行驶一周。
提示:
- gas.length == n
- cost.length == n
- 1 <= n <= 105
- 0 <= gas[i], cost[i] <= 104
方法一:
函数图像法:
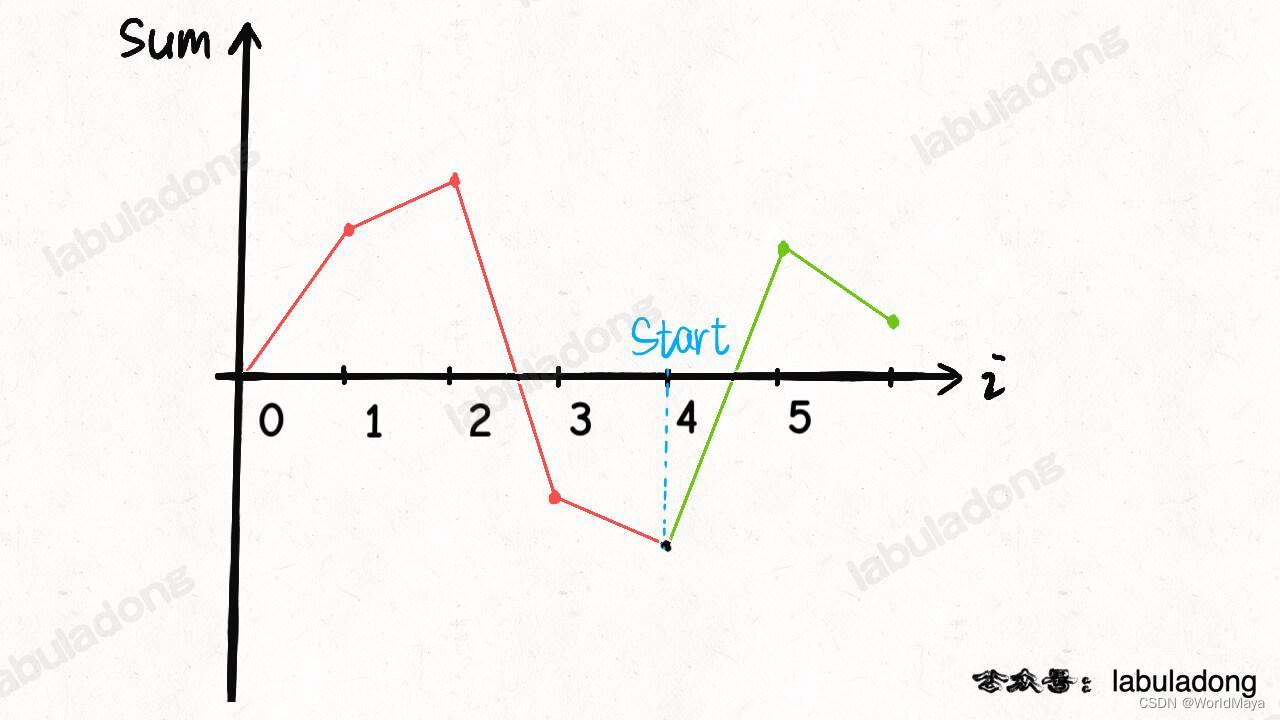
sum 代表路途中油箱的油量,如果把这个「最低点」作为起点,即把这个点作为坐标轴原点,就相当于把图像「最大限度」向上平移了:
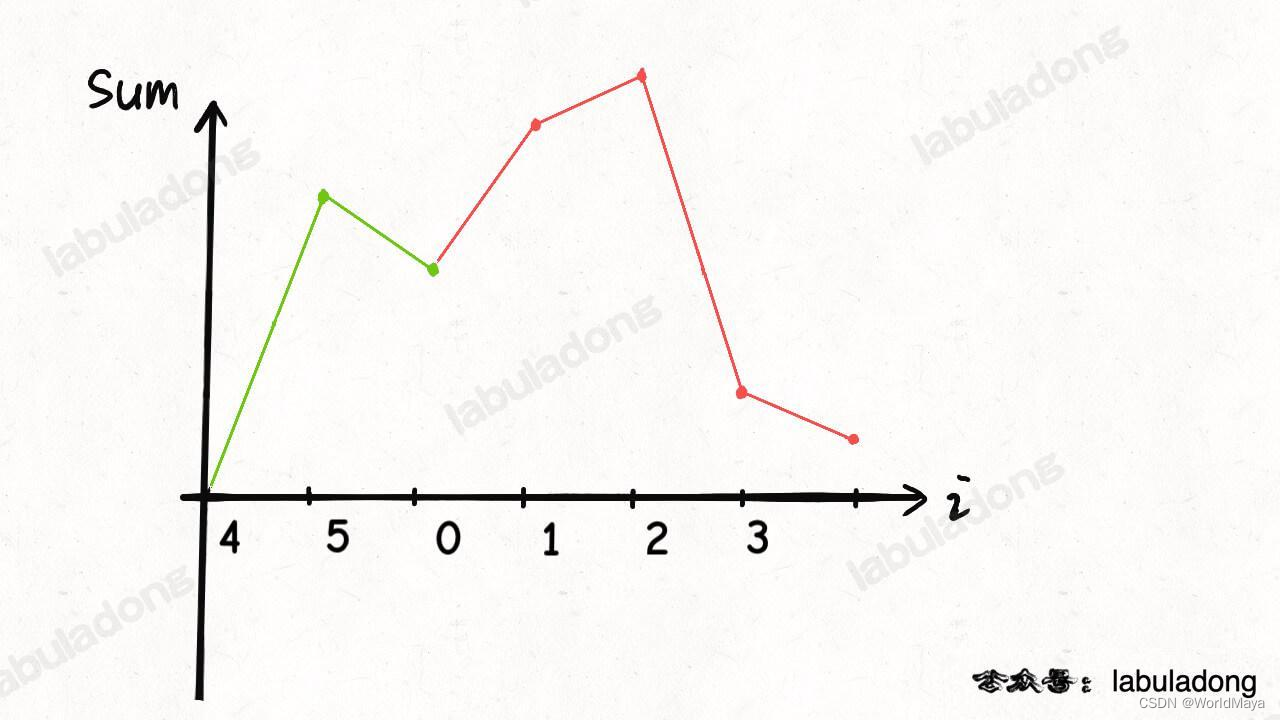
如果经过平移后图像全部在 x 轴以上,就说明可以行使一周。
代码一:
class Solution {
public:int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {int n = gas.size();int minsum = 0, minpos = 0; //函数最低点的值,函数最低点的坐标(出发站编号)int sum = 0;for(int i = 0; i < n; i++){sum += gas[i] - cost[i];if(sum < minsum) {minsum = sum;minpos = i + 1;}}if(sum < 0) return -1;return minpos % n;}
};
时间复杂度O(n),空间复杂度O(1)。
方法二:
贪心解法:
用贪心思路解决这道题的关键在于以下这个结论:
如果选择站点i作为起点「恰好」无法走到站点j,那么i和j中间的任意站点k都不可能作为起点。
比如说,如果从站点1出发,走到站点5时油箱中的油量「恰好」减到了负数,那么说明站点1「恰好」无法到达站点5;那么你从站点2,3,4任意一个站点出发都无法到达5,因为到达站点5时油箱的油量也必然被减到负数。
如何证明这个结论?
假设sum记录当前油箱中的油量,如果从站点i出发(sum = 0),走到j时恰好出现sum < 0的情况,那说明走到i, j之间的任意站点k时都满足sum > 0,对吧。
如果把k作为起点的话,相当于在站点k时sum = 0,那走到j时必然有sum < 0,也就是说k肯定不能是起点。
拜托,从i出发走到k好歹sum > 0,都无法达到j,现在你还让sum = 0了,那更不可能走到j了对吧。
综上,这个结论就被证明了。
回想一下我们开头说的暴力解法是怎么做的?
如果我发现从i出发无法走到j,那么显然i不可能是起点。
现在,我们发现了一个新规律,可以推导出什么?
如果我发现从i出发无法走到j,那么i以及i, j之间的所有站点都不可能作为起点。
看到冗余计算了吗?看到优化的点了吗?
这就是贪心思路的本质,如果找不到重复计算,那就通过问题中一些隐藏较深的规律,来减少冗余计算。
代码二:
class Solution {
public:int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {int n = gas.size();for(int i = 0; i < n;){int sum = 0;bool flag = true; //以i为出发站时能否环行一周for(int j = i; j < i + n; j++){sum += gas[j % n] - cost[j % n]; //行至第j+1个加油站时,油箱内的油量if(sum < 0) {if(j + 1 >= n) return -1; //全部出发点已遍历完,未找到可行解i = (j + 1) % n; //无法从第i站到第j+1站,则从中间任意一站都无法到第j+1站。那么以第j+1站为出发站继续检查flag = false;break;}}if(flag) return i; //以第i站为出发站可以走完一周,返回i}return -1;}
};
时间复杂度O(n),空间复杂度O(1)。
相关文章:

LeetCode 134. 加油站(函数图像法 / 贪心)
题目: 链接:LeetCode 134. 加油站 难度:中等 在一条环路上有 n 个加油站,其中第 i 个加油站有汽油 gas[i] 升。 你有一辆油箱容量无限的的汽车,从第 i 个加油站开往第 i1 个加油站需要消耗汽油 cost[i] 升。你从其中…...

王道计算机组成原理课代表 - 考研计算机 第三章 存储系统 究极精华总结笔记
本篇博客是考研期间学习王道课程 传送门 的笔记,以及一整年里对 计算机组成 知识点的理解的总结。希望对新一届的计算机考研人提供帮助!!! 关于对 存储系统 章节知识点总结的十分全面,涵括了《计算机组成原理》课程里…...
Flask-mock接口数据流程
背景:由于在开发过程中,会遇到以下的痛点 1.服务端接口提测延期,具体接口逻辑未完成实现,接口未能正常调通,导致客户端提测停滞; 2.因为前期已在技术评审上已与客户端开发定好接口字段,客户端比…...

springboot项目配置序列化,反序列化器
介绍本文介绍在项目中时间类型、枚举类型的序列化和反序列化自定义的处理类,也可以使用注解。建议枚举都实现一个统一的接口,方便处理。我这定义了一个Dict接口。枚举类型注解处理这种方式比较灵活,可以让枚举按照自己的方式序列化࿰…...
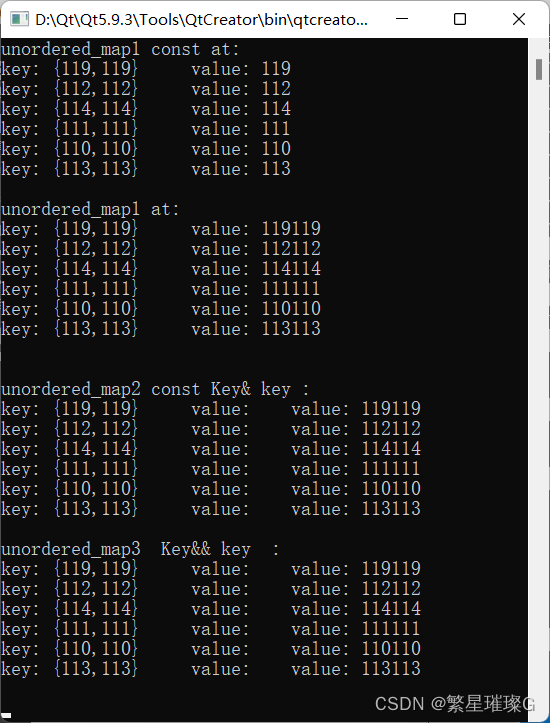
c++11 标准模板(STL)(std::unordered_map)(九)
定义于头文件 <unordered_map> template< class Key, class T, class Hash std::hash<Key>, class KeyEqual std::equal_to<Key>, class Allocator std::allocator< std::pair<const Key, T> > > class unordered…...

Seay代码审计工具
一、简介Seay是基于C#语言开发的一款针对PHP代码安全性审计的系统,主要运行于Windows系统上。这款软件能够发现SQL注入、代码执行、命令执行、文件包含、文件上传、绕过转义防护、拒绝服务、XSS跨站、信息泄露、任意URL跳转等漏洞,基本上覆盖常见PHP漏洞…...
界面开发(4)--- PyQt5实现打开图像及视频播放功能
PyQt5创建打开图像及播放视频页面 上篇文章主要介绍了如何实现登录界面的账号密码注册及登录功能,还简单介绍了有关数据库的连接方法。这篇文章我们介绍一下如何在设计的页面中打开本地的图像,以及实现视频播放功能。 实现打开图像功能 为了便于记录实…...
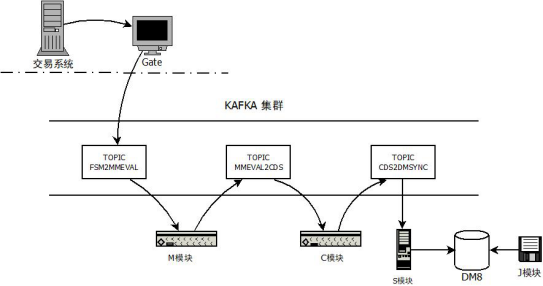
核心系统国产平台迁移验证
核心系统国产平台迁移验证 摘要:信息技术应用创新,旨在实现信息技术领域的自主可控,保障国家信息安全。金融领域又是关系国家经济命脉的行业,而对核心交易系统的信息技术应用创新是交易所未来将要面临的重大挑战。为了推进国产化进…...

【数据结构之二叉树】——二叉树的概念及结构,特殊的二叉树和二叉树性质
文章目录一、二叉树的概念及结构1.概念2.现实中的二叉树3. 特殊的二叉树:3.二叉树的性质二、二叉树练习题总结一、二叉树的概念及结构 1.概念 一棵二叉树是结点的一个有限集合,该集合: 或者为空由一个根节点加上两棵别称为左子树和右子树的二叉树组成…...

Android学习之帧动画和视图动画
帧动画 帧动画中的每一帧其实都是一张图片,将许多图片连起来播放,就形成了帧动画。 在drawable目录下新建frmae_animation文件,在这个文件中定义了帧动画的每一帧要显示的图片,播放时,按从上到下显示。 <?xml v…...

vue2和vue3的区别
这周呢主要就是整理整理学的东西,不然看的也记不住,把这些学的东西做成笔记,感觉会清楚许多,这次就把vue2和vue3的区别总结一下,明天要考四级,嗐,本来想着复习四级,结果只写了一两套…...
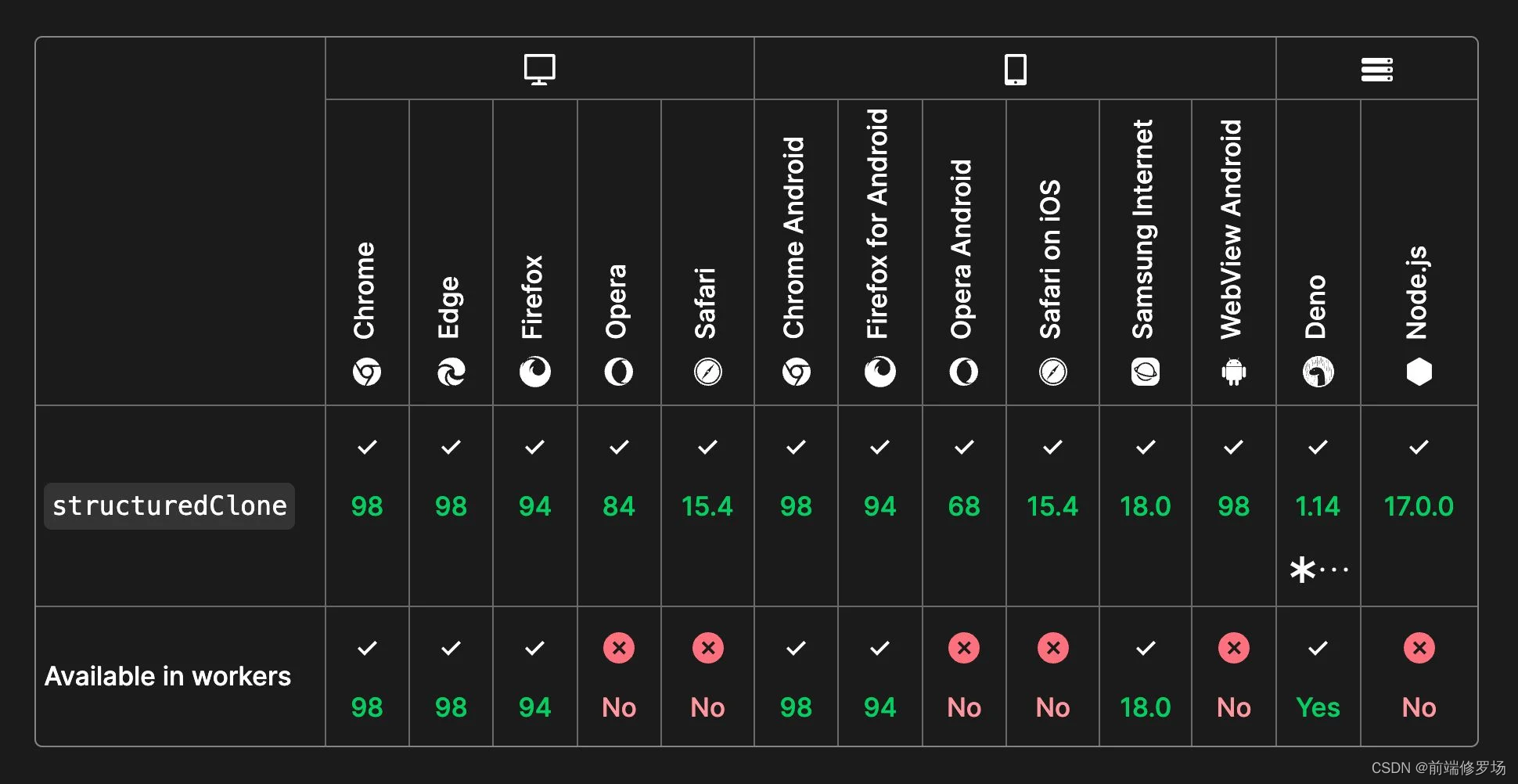
【你不知道的事】JavaScript 中用一种更先进的方式进行深拷贝:structuredClone
你是否知道,JavaScript中有一种原生的方法来做对象的深拷贝? 本文我们要介绍的是 structuredClone 函数,它是内置在 JavaScript 运行时中的: const calendarEvent {title: "Builder.io Conf",date: new Date(123),attendees: ["Steve…...
XE开发Linux应用(二)-Webservice
新建一个工程。选择如图。继续输入服务名然后就生成对应的单元。增加linux 平台。完善对应的单元代码{ Invokable implementation File for Txaliontest which implements Ixaliontest }unit xaliontestImpl;interfaceuses Soap.InvokeRegistry, System.Types, Soap.XSBuiltIns…...

kubernetes实战与源码学习
1.1 关于Kubernetes的介绍与核心对象概念 关于Kubernetes的介绍与核心对象概念-阿里云开发者社区 k8s架构 核心对象 使用kubeadm10分钟部署k8集群 使用 KuboardSpray 安装kubernetes_v1.23.1 | Kuboard k8s-上部署第一个应用程序 Deployment基本概念 给应用添加service&a…...

CNCF x Alibaba云原生技术公开课 第八章 应用配置管理
Pod配置管理分类 可变配置就用 ConfigMap;敏感信息是用 Secret;身份认证是用 ServiceAccount;资源配置是用 Resources;安全管控是用 SecurityContext;前置校验是用 InitContainers。 1、ConfigMap 概念:…...

YUV实践记录
文章目录YUV基础介绍:不同采样YUV格式的区别为什么要使用YUV格式呢?YUV的存储方式Android中的YUV_420_888附录:YUV基础介绍: YUV在做手机图像或者视频处理的时候会经常用到的一个格式,用此文来记录YUV相关介绍…...

【题解】百度2020校招Web前端工程师笔试卷(第一批):单选题、多选题
题目来源 若有错误请指正! 单选 1 分页存储管理将进程的逻辑地址空间分成若干个页,并为各页加以编号,从0开始,若某一计算机主存按字节编址,逻辑地址和物理地址都是32位,页表项大小为4字节,若…...
)
探索云原生技术之容器编排引擎-kubeadm安装kubernetes1.21.10(新版:针对高版本内核)
❤️作者简介:2022新星计划第三季云原生与云计算赛道Top5🏅、华为云享专家🏅、云原生领域潜力新星🏅 💛博客首页:C站个人主页🌞 💗作者目的:如有错误请指正,将…...

2023广西自治区职业技能大赛“网络安全” 项目比赛任务书
2023广西自治区职业技能大赛“网络安全” 项目比赛任务书2023广西自治区职业技能大赛“网络安全” 项目比赛任务书A模块基础设施设置/安全加固(200分)A-1:登录安全加固(Windows, Linux)A-2:Nginx安全策略&a…...
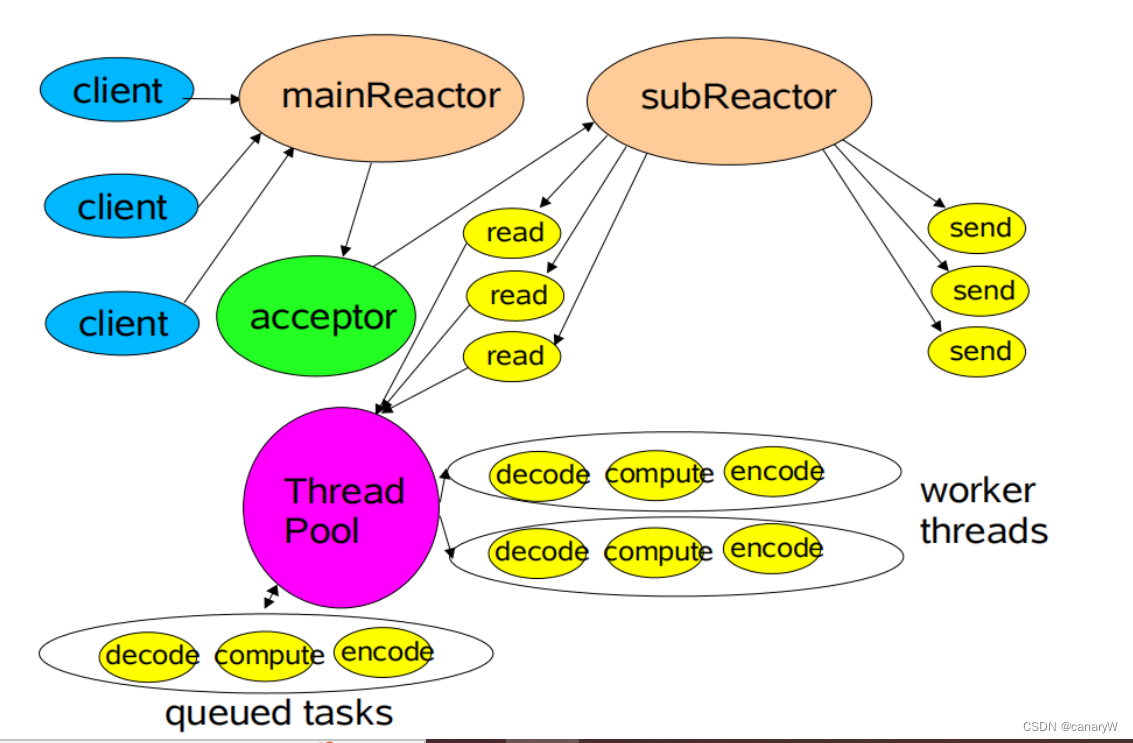
Reactor模式
Reactor是一种设计模式,可以用于构建高并发的网络服务器。 Reactor模式的好处在于:可以在一个或多个reactor线程使用多路复用技术去管理所有网络连接连接建立、IO请求,保证工作线程不被IO阻塞。 前置知识:IO多路复用技术 1. 传统网…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...

适应性Java用于现代 API:REST、GraphQL 和事件驱动
在快速发展的软件开发领域,REST、GraphQL 和事件驱动架构等新的 API 标准对于构建可扩展、高效的系统至关重要。Java 在现代 API 方面以其在企业应用中的稳定性而闻名,不断适应这些现代范式的需求。随着不断发展的生态系统,Java 在现代 API 方…...

【Linux】自动化构建-Make/Makefile
前言 上文我们讲到了Linux中的编译器gcc/g 【Linux】编译器gcc/g及其库的详细介绍-CSDN博客 本来我们将一个对于编译来说很重要的工具:make/makfile 1.背景 在一个工程中源文件不计其数,其按类型、功能、模块分别放在若干个目录中,mak…...
