【动态规划】2306. 公司命名
本文涉及知识点
动态规划汇总
LeetCode 2306. 公司命名
给你一个字符串数组 ideas 表示在公司命名过程中使用的名字列表。公司命名流程如下:
从 ideas 中选择 2 个 不同 名字,称为 ideaA 和 ideaB 。
交换 ideaA 和 ideaB 的首字母。
如果得到的两个新名字 都 不在 ideas 中,那么 ideaA ideaB(串联 ideaA 和 ideaB ,中间用一个空格分隔)是一个有效的公司名字。
否则,不是一个有效的名字。
返回 不同 且有效的公司名字的数目。
示例 1:
输入:ideas = [“coffee”,“donuts”,“time”,“toffee”]
输出:6
解释:下面列出一些有效的选择方案:
- (“coffee”, “donuts”):对应的公司名字是 “doffee conuts” 。
- (“donuts”, “coffee”):对应的公司名字是 “conuts doffee” 。
- (“donuts”, “time”):对应的公司名字是 “tonuts dime” 。
- (“donuts”, “toffee”):对应的公司名字是 “tonuts doffee” 。
- (“time”, “donuts”):对应的公司名字是 “dime tonuts” 。
- (“toffee”, “donuts”):对应的公司名字是 “doffee tonuts” 。
因此,总共有 6 个不同的公司名字。
下面列出一些无效的选择方案:
- (“coffee”, “time”):在原数组中存在交换后形成的名字 “toffee” 。
- (“time”, “toffee”):在原数组中存在交换后形成的两个名字。
- (“coffee”, “toffee”):在原数组中存在交换后形成的两个名字。
示例 2:
输入:ideas = [“lack”,“back”]
输出:0
解释:不存在有效的选择方案。因此,返回 0 。
提示:
2 <= ideas.length <= 5 * 104
1 <= ideas[i].length <= 10
ideas[i] 由小写英文字母组成
ideas 中的所有字符串 互不相同
动态规划的状态表示
n = ideas.length
m = ideas[i].length
dp[j][k] 表示处理完ideas[0…i-1],符合以下条件的ideas数量:
首字母可以换成‘a’+j,首字符为’a’+k。
空间复杂度:O( ∑ ∑ \sum\sum ∑∑) ∑ \sum ∑是字符集的大小,此处为26。
动态规划的转移方程
tmp = ideas[i];
for( j = 0 ; j < 26;j++)
{
tmp[0] = ‘a’+j;
如果tmp不存在 dp[j][ideas[i][0]-‘a’]++;
}
单个状态的转移方程时间复杂度:O(m+ ∑ \sum ∑)
总时间复杂度:O(n × ( m + ∑ ) \times (m+\sum) ×(m+∑))
动态规划的初值
全为0。
动态规划的填表顺序
i从0到大
动态规划的返回值
tmp = ideas[i];
for( j = 0 ; j < 26;j++)
{
tmp[0] = ‘a’+j;
如果tmp不存在 ret += dp[ideas[i][0]-‘a’][j]
}
最终返回值:ret*2 ,只枚举了下标小的在前面,其实下标小的可以在后面。
** 注意** : 返回值的循环和转移方程的循环不能合并,且先处理返回值。
代码
核心代码
class Solution{
public:long long distinctNames(vector<string>&ideas) {int dp[26][26] = { 0 };unordered_set<string> sHas(ideas.begin(), ideas.end());long long ret = 0;for (const auto& s : ideas) {const int inx = s[0] - 'a';auto tmp = s;for (int j = 0; j < 26; j++) {tmp[0] = 'a' + j;if (!sHas.count(tmp)) {ret += dp[inx][j];}}for (int j = 0; j < 26; j++) {tmp[0] = 'a' + j;if (!sHas.count(tmp)) {dp[j][inx]++;}}}return ret*2;}
};
单元测试
template<class T1, class T2>
void AssertEx(const T1& t1, const T2& t2)
{Assert::AreEqual(t1, t2);
}template<class T>
void AssertEx(const vector<T>& v1, const vector<T>& v2)
{Assert::AreEqual(v1.size(), v2.size());for (int i = 0; i < v1.size(); i++){Assert::AreEqual(v1[i], v2[i]);}
}template<class T>
void AssertV2(vector<vector<T>> vv1, vector<vector<T>> vv2)
{sort(vv1.begin(), vv1.end());sort(vv2.begin(), vv2.end());Assert::AreEqual(vv1.size(), vv2.size());for (int i = 0; i < vv1.size(); i++){AssertEx(vv1[i], vv2[i]);}
}namespace UnitTest
{ vector<string> ideas;TEST_CLASS(UnitTest){public:TEST_METHOD(TestMethod00){ideas = { "coffee", "donuts", "time", "toffee" };auto res = Solution().distinctNames(ideas);AssertEx(6LL, res);}TEST_METHOD(TestMethod01){ideas = { "lack","back" };auto res = Solution().distinctNames(ideas);AssertEx(0LL, res);}};
}返回值优化
累加:dp[i][j]和dp[j][i]相乘
class Solution{
public:long long distinctNames(vector<string>&ideas) {int dp[26][26] = { 0 };unordered_set<string> sHas(ideas.begin(), ideas.end()); for (const auto& s : ideas) {const int inx = s[0] - 'a';auto tmp = s;for (int j = 0; j < 26; j++) {tmp[0] = 'a' + j;if (!sHas.count(tmp)) {dp[j][inx]++;}}}long long ret = 0;for (int i = 0; i < 26; i++) {for (int j = 0; j < 26; j++) {ret += (long long)dp[i][j] * dp[j][i];}}return ret;}
};

扩展阅读
视频课程
先学简单的课程,请移步CSDN学院,听白银讲师(也就是鄙人)的讲解。
https://edu.csdn.net/course/detail/38771
如何你想快速形成战斗了,为老板分忧,请学习C#入职培训、C++入职培训等课程
https://edu.csdn.net/lecturer/6176
相关推荐
| 我想对大家说的话 |
|---|
| 《喜缺全书算法册》以原理、正确性证明、总结为主。 |
| 按类别查阅鄙人的算法文章,请点击《算法与数据汇总》。 |
| 有效学习:明确的目标 及时的反馈 拉伸区(难度合适) 专注 |
| 闻缺陷则喜(喜缺)是一个美好的愿望,早发现问题,早修改问题,给老板节约钱。 |
| 子墨子言之:事无终始,无务多业。也就是我们常说的专业的人做专业的事。 |
| 如果程序是一条龙,那算法就是他的是睛 |
测试环境
操作系统:win7 开发环境: VS2019 C++17
或者 操作系统:win10 开发环境: VS2022 C++17
如无特殊说明,本算法用**C++**实现。

相关文章:

【动态规划】2306. 公司命名
本文涉及知识点 动态规划汇总 LeetCode 2306. 公司命名 给你一个字符串数组 ideas 表示在公司命名过程中使用的名字列表。公司命名流程如下: 从 ideas 中选择 2 个 不同 名字,称为 ideaA 和 ideaB 。 交换 ideaA 和 ideaB 的首字母。 如果得到的两个新…...
熟练掌握爬虫技术
一、Crawler、Requests反爬破解 1. HTTP协议与WEB开发 1. 什么是请求头请求体,响应头响应体 2. URL地址包括什么 3. get请求和post请求到底是什么 4. Content-Type是什么1.1 简介 HTTP协议是Hyper Text Transfer Protocol(超文本传输协议)…...
基于Spring Boot与Vue的智能房产匹配平台+文档
博主介绍:✌在职Java研发工程师、专注于程序设计、源码分享、技术交流、专注于Java技术领域和毕业设计✌ 温馨提示:文末有 CSDN 平台官方提供的老师 Wechat / QQ 名片 :) Java精品实战案例《700套》 2025最新毕业设计选题推荐:最热的500个选题…...

【VMware】VMware 开启的虚拟机无法联网的解决方案
目录 🌊1. 问题说明 🌊2. 解决方案 🌍2.1 查看虚拟网络编辑器 🌍2.2 设置 vmnet 🌍2.3 设置虚拟机网络 🌍2.4 Xshell连接虚拟机 🌊1. 问题说明 虚拟机 ping 其他网页显示失败,比如&#…...

linux——线程
在 Linux 系统中,进程和线程是两种重要的并发执行单元。本文将详细介绍它们的区别、使用场景、以及多线程编程中的关键API和示例代码。 进程与线程的区别 进程 进程是程序运行的一个实例,承担分配系统资源的基本单位。每个进程都有独立的地址空间&…...

install nebula with source
linux 环境:ubuntu 2004 默认gcc 7.5 nebula requerment: g 8.5 above 下载source git clone --branch release-3.8 https://github.com/vesoft-inc/nebula.git install gcc g 11 apt install gcc-11 g-11 此时 linux环境存在多个版本gcc:…...

拆分盘投资策略解析:机制、案例与风险考量
一、引言 随着互联网技术的迅猛发展和金融市场的不断创新,拆分盘这一投资模式逐渐崭露头角,成为投资者关注的焦点。它基于特定的拆分策略,通过调整投资者持有的份额和单价,实现了看似稳健的资产增长。本文旨在深入探讨拆分盘的运…...

Redis主从复制、哨兵模式以及Cluster集群
一.主从复制 1.主从复制的概念 主从复制,是指将一台Redis服务器的数据,复制到其他的Redis服务器。前者称为主节点(Master),后者称为从节点(Slave);数据的复制是单向的,只能由主节点到从节点。默认情况下,…...

【chatgpt】npy文件和npz文件区别
npy文件和npz文件都是用于存储NumPy数组的文件格式。它们的主要区别如下: npy文件:这种文件格式用于存储单个NumPy数组。它是一种简单的二进制文件格式,可以快速地读写NumPy数组。 npz文件:这种文件格式是一个压缩包,…...

为什么IP地址会被列入黑名单?
您是否曾经历过网站访客数量骤减或电子邮件投递失败的困扰?这背后或许隐藏着一个常被忽略的原因:您的IP地址可能已经被列入了黑名单内。尽管您并没有进行任何违法的网络操作,但这个问题依然可能出现。那么,究竟黑名单是什么&#…...

【OceanBase诊断调优】—— 如何查找表被哪些其它表引用外键
本文详述如何查找指定表是否被其他表引用做外键。 适用版本 OceanBase 数据库所有版本。 MySQL 租户 obclient> select * from INFORMATION_SCHEMA.KEY_COLUMN_USAGE where REFERENCED_TABLE_NAME表名;Oracle 租户 obclient> SELECT TABLE_NAME FROM dba_constraint…...
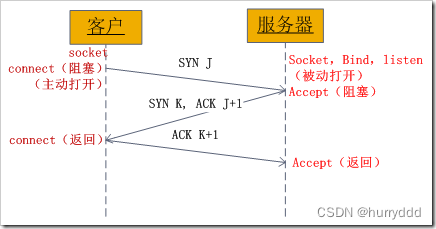
网络编程常见问题
1、TCP状态迁移图 2、TCP三次握手过程 2.1、握手流程 1、TCP服务器进程先创建传输控制块TCB,时刻准备接受客户进程的连接请求,此时服务器就进入了LISTEN(监听)状态; 2、TCP客户进程也是先创建传输控制块TCBÿ…...

回调函数的使用详解
实际工作中,经常使用回调函数。用来实现触发等机制,也是基于一些已开发好的底层平台,开发上层应用的常用方法。下面对回调函数做一个详细的解释。 目录 1. 简单的回调函数实例 2. C11,使用function<>的写法 3. 注册函数 …...
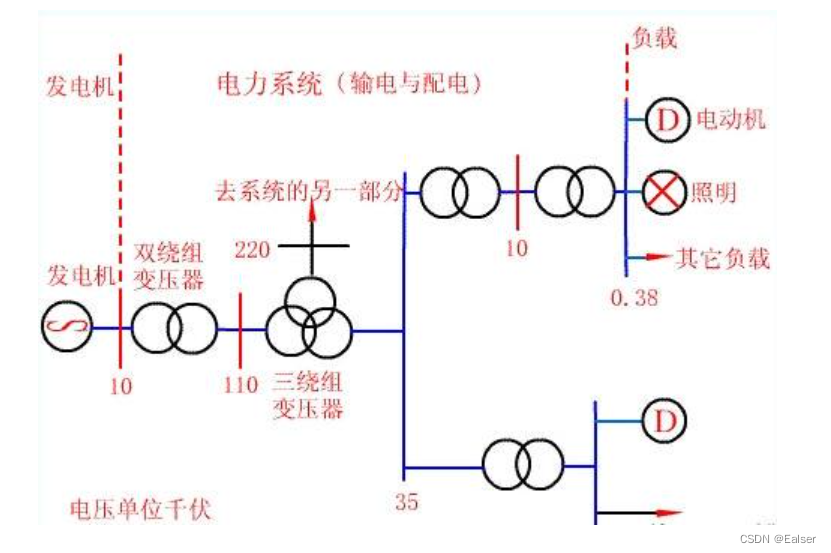
<电力行业> - 《第8课:输电(一)》
1 输电环节的意义 电能的传输,是电力系统整体功能的重要组成环节。发电厂与电力负荷中心通常都位于不同地区。在水力、煤炭等一次能源资源条件适宜的地点建立发电厂,通过输电可以将电能输送到远离发电厂的负荷中心,使电能的开发和利用超越地…...

【python学习】 __pycache__ 文件是什么
__pycache__文件是Python中的一个特殊目录,主要用于存储已编译的字节码文件(.pyc文件)。以下是关于__pycache__文件的详细解释: 作用:当Python解释器执行一个模块时,它会首先检查是否存在对应的.pyc文件。…...
论文阅读_基本于文本嵌入的信息提取
英文名:Embedding-based Retrieval with LLM for Effective Agriculture Information Extracting from Unstructured Data 中文名:基于嵌入的检索,LLM 从非结构化数据中提取有效的农业信息 地址: https://arxiv.org/abs/2308.03107 时间&…...

kafka学习笔记08
Springboot项目整合spring-kafka依赖包配置 有这种方式,就是可以是把之前test里的配置在这写上,用Bean注解上。 现在来介绍第二种方式: 1.添加kafka依赖: 2.添加kafka配置方式: 编写代码发送消息: 测试: …...

Flask的 preprocess_request
理解 Flask 类似框架中的 preprocess_request 方法 在 Flask 类似的 web 框架中,preprocess_request 方法是一个关键组件。它在请求被分派之前调用,用于执行一些预处理操作。让我们一步一步来理解这个方法的工作原理。 1. 方法概述 首先,我…...
)
重温react-05(类组件生命周期和性能优化)
类组件的生命周期 import React, { Component } from reactexport default class learnReact05 extends Component {state {number: 1}render() {return (<div>{this.state.number}</div>)}// 一般将请求的方法,放在这个生命周期componentDidMount() {setInterva…...
RHCE四---web服务器的高级优化方案
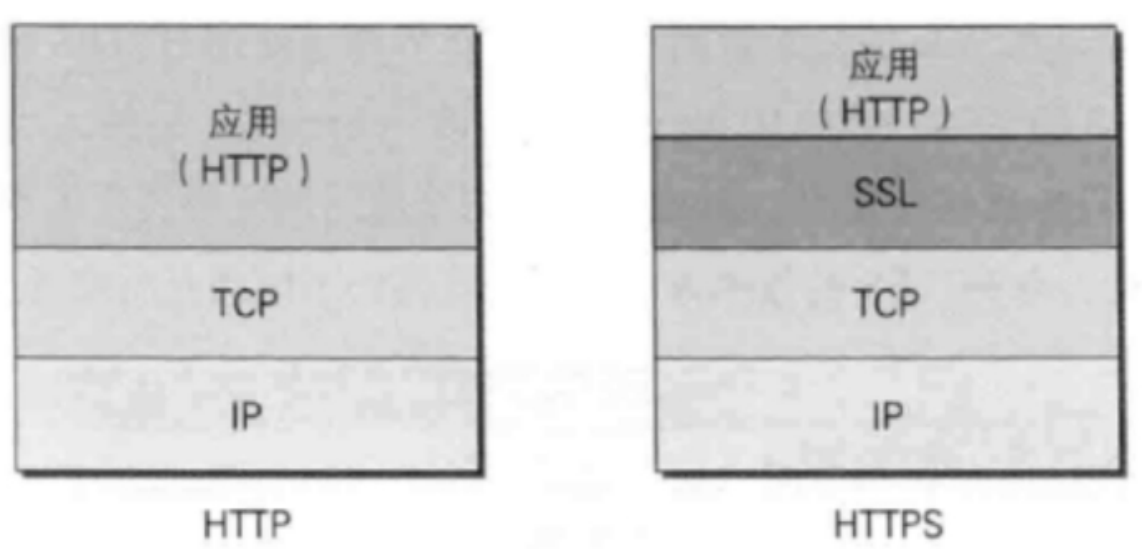
一、Web服务器(2) 基于https协议的静态网站 概念解释 HTTPS(全称:Hyper Text Transfer Protocol over Secure Socket Layer 或 Hypertext TransferProtocol Secure,超文本传输安全协议),是以…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...
