LeetCode 算法:翻转二叉树 c++
原题链接🔗:翻转二叉树
难度:简单⭐️
题目
给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点。
示例 1:
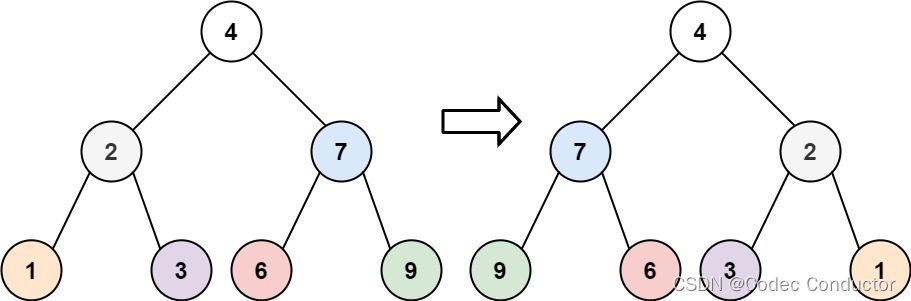
输入:root = [4,2,7,1,3,6,9]
输出:[4,7,2,9,6,3,1]
示例 2:
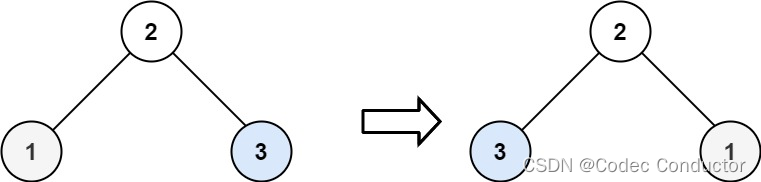
输入:root = [2,1,3]
输出:[2,3,1]
示例 3:
输入:root = []
输出:[]
提示:
- 树中节点数目范围在 [0, 100] 内
- -100 <= Node.val <= 100
题解
递归法
解题思路: 翻转二叉树的解题思路主要基于递归和树的遍历。以下是详细的步骤和思路:
理解问题:首先,明确题目要求翻转二叉树,即将每个节点的左子树和右子树互换。
递归方法:递归是解决这个问题的自然选择,因为它可以很好地处理树结构的遍历。
递归终止条件:递归的基本终止条件是当节点为空时,不需要翻转,直接返回
nullptr。递归逻辑:
- 在递归到每个节点时,首先交换当前节点的左子树和右子树。
- 然后,递归地翻转当前节点的左子树(原来的右子树)。
- 接着,递归地翻转当前节点的右子树(原来的左子树)。
递归返回值:在递归调用结束后,返回当前节点。虽然在翻转操作中,我们关心的是操作本身而不是返回值,但递归需要返回值来构建翻转后的树结构。
编写递归函数:实现递归函数,使用条件语句来处理递归终止条件,并使用递归调用来翻转子树。
测试:使用不同的二叉树结构来测试你的翻转算法,确保它可以正确地翻转所有类型的树。
优化:考虑算法的时间复杂度和空间复杂度。翻转操作的时间复杂度是O(n),其中n是树中的节点数,因为每个节点恰好被访问一次。空间复杂度是O(h),其中h是树的高度,这是因为递归调用的深度。
边界条件:确保处理了所有边界条件,如空树或只有一个节点的树。
代码实现:将上述思路转化为代码实现。
- 复杂度:
- 时间复杂度是 O(N),其中 N 为二叉树节点的数目。我们会遍历二叉树中的每一个节点,对每个节点而言,我们在常数时间内交换其两棵子树;
- 空间复杂度是 O(N),使用的空间由递归栈的深度决定,它等于当前节点在二叉树中的高度。在平均情况下,二叉树的高度与节点个数为对数关系,即 O(logN)。而在最坏情况下,树形成链状,空间复杂度为 O(N)。
- c++ demo:
#include <iostream>
#include <queue>// 定义二叉树节点
struct TreeNode {int val;TreeNode* left;TreeNode* right;TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};// 翻转二叉树的解决方案
class Solution {
public:TreeNode* invertTree(TreeNode* root) {if (!root) return nullptr; // 递归终止条件:如果节点为空,返回nullptrstd::swap(root->left, root->right); // 交换当前节点的左右子树invertTree(root->left); // 递归翻转左子树invertTree(root->right); // 递归翻转右子树return root; // 返回翻转后的树的根节点}
};// 辅助函数:按层序遍历打印二叉树
void printLevelOrder(TreeNode* root) {if (!root) return;std::queue<TreeNode*> q;q.push(root);while (!q.empty()) {TreeNode* node = q.front();q.pop();if (node->left) q.push(node->left);if (node->right) q.push(node->right);std::cout << node->val << " ";}std::cout << std::endl;
}// 主函数
int main() {Solution solution;// 创建示例二叉树// 4// / \// 2 7// / \ / \// 1 3 6 9TreeNode* root = new TreeNode(4);root->left = new TreeNode(2);root->right = new TreeNode(7);root->left->left = new TreeNode(1);root->left->right = new TreeNode(3);root->right->left = new TreeNode(6);root->right->right = new TreeNode(9);std::cout << "Original binary tree:" << std::endl;printLevelOrder(root);// 翻转二叉树TreeNode* invertedRoot = solution.invertTree(root);std::cout << "Inverted binary tree:" << std::endl;printLevelOrder(invertedRoot);// 清理分配的内存delete root->left->left;delete root->left->right;delete root->left;delete root->right->left;delete root->right->right;delete root->right;delete root;return 0;
}
- 输出结果:
Original binary tree:
4 2 7 1 3 6 9
Inverted binary tree:
4 7 2 9 6 3 1
相关文章:
LeetCode 算法:翻转二叉树 c++
原题链接🔗:翻转二叉树 难度:简单⭐️ 题目 给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点。 示例 1: 输入:root [4,2,7,1,3,6,9] 输出:[4,7,2,9,6,3,1] 示例 …...
七天速通javaSE:第五天 数组进阶
文章目录 前言一、二维数组二、Arrays类1.toString打印数组内各元素1.1 示例1.2 自己实现内部逻辑 2. sort升序排列3. fill数组填充(重新赋值)4.equals比较数组元素是否相等 三、冒泡排序 前言 本文将学习二维数组、arrays类以及冒泡排序 一、二维数组 …...

游戏心理学Day28
独立游戏团队架构 独立游戏工作室是一个包括编程美术设计院校项目管理和运营等各种职能的团队找到可以共同奋斗。数月甚至数年的合适人选并不是一件容易的事情。游戏开发过程中要涉及多种常规工作。小团队的每个成员通常都要身兼数职,而且有些角色常由多人担任。 …...

鸿蒙开发设备管理:【@ohos.multimodalInput.inputEventClient (注入按键)】
注入按键 InputEventClient模块提供了注入按键能力。 说明: 本模块首批接口从API version 8开始支持。后续版本的新增接口,采用上角标单独标记接口的起始版本。本模块接口均为系统接口,三方应用不支持调用。 导入模块 import inputEventCli…...

C++:std::function的libc++实现
std::function是个有点神奇的模板,无论是普通函数、函数对象、lambda表达式还是std::bind的返回值(以上统称为可调用对象(Callable)),无论可调用对象的实际类型是什么,无论是有状态的还是无状态…...
DM 的断点续传测试
作者: 大鱼海棠 原文来源: https://tidb.net/blog/4540ae34 一、概述 DM有all、full、incremental三种数据迁移同步方式(task-mode),在all同步模式下,因一些特殊情况,需要变更上游MySQL的数…...

力扣每日一题 6/30 记忆化搜索/动态规划
博客主页:誓则盟约系列专栏:IT竞赛 专栏关注博主,后期持续更新系列文章如果有错误感谢请大家批评指出,及时修改感谢大家点赞👍收藏⭐评论✍ 494.目标和【中等】 题目: 给你一个非负整数数组 nums 和一个…...

图像基础知识入门【图像概念不同图像格式】
图像基础知识入门【图像概念&不同图像格式】 最近有在处理图像转换,因此稍微补足了一下图像相关知识,特在此记录。下面汇总是我根据自己理解和网上查阅资料而来。如有错误,欢迎大家指正。 1 基础概念 像素/分辨率 像素(Pixel)ÿ…...

HP服务器基于SNMP-ilo4的硬件监控指标解读
监控易是一款功能全面的IT基础设施监控软件,它通过SNMP协议与HP服务器内置的ilo4远程管理卡进行通信,实现对HP服务器硬件状态的实时监控。本文将针对监控易中基于SNMP-ilo4的HP服务器硬件监控指标进行解读,帮助运维团队更好地理解和应用这些监…...

Android13系统导航栏添加音量加减键按钮功能
不知道为什么拿到芯片原厂发布给我们的Android13系统源码编译后,导航栏没有音量加减键,客户有反馈这个问题,所以特意加了一下,修改记录如下:frameworks/base目录下 commit 9cb2244d61a237cab03c540bfcca6e4fac2bea2c …...

普及GIS知识,推动产业发展
915 GIS节:普及GIS知识,推动产业发展 自2008年起,每年的9月15日被定为“GIS节”,这一特殊的节日由超图首次发起倡议,旨在打造一个普及和传播GIS(地理信息系统)知识的平台,促进大众对…...
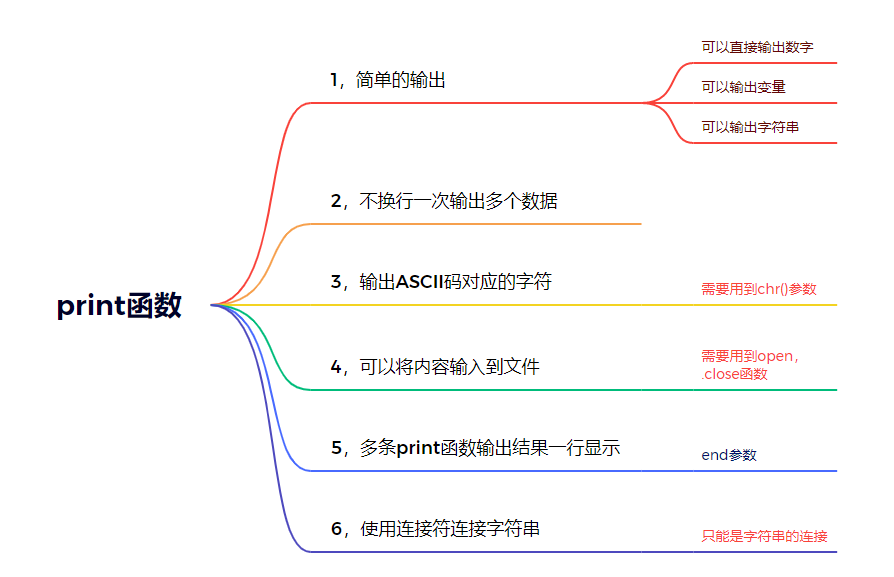
第2章-Python编程基础
#本章目标 1,了解什么是计算机程序 2,了解什么是编程语言 3,了解编程语言的分类 4,了解静态语言与脚本语言的区别 5,掌握IPO程序编写方法 6,熟练应用输出函数print与输入函数input 7,掌握Python…...
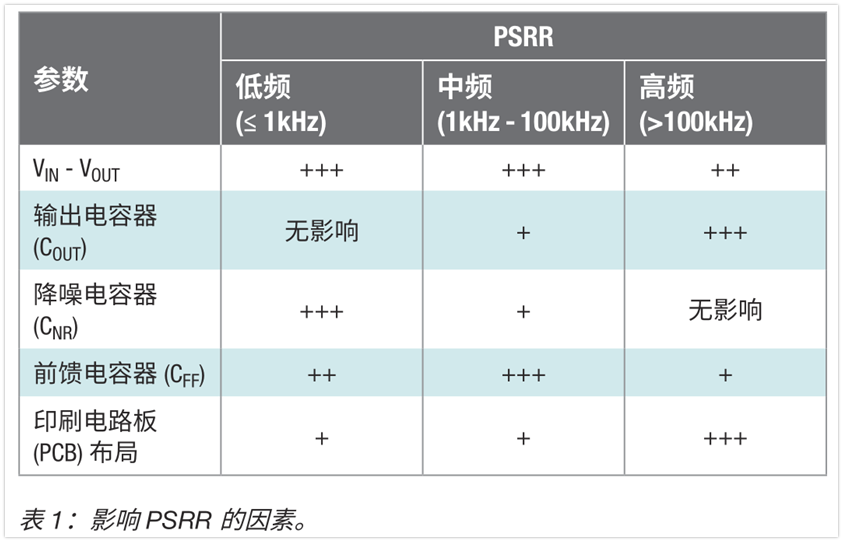
LDO产品的基础知识解析
低压降稳压器 (LDO)是一种用于调节较高电压输入产生的输出电压的简单方法。在大多数情况下,低压降稳压器都易于设计和使用。然而,如今的现代应用都包括各种各样的模拟和数字系统,而有些系统和工作条件将决定哪种LDO最适合相关电路,…...
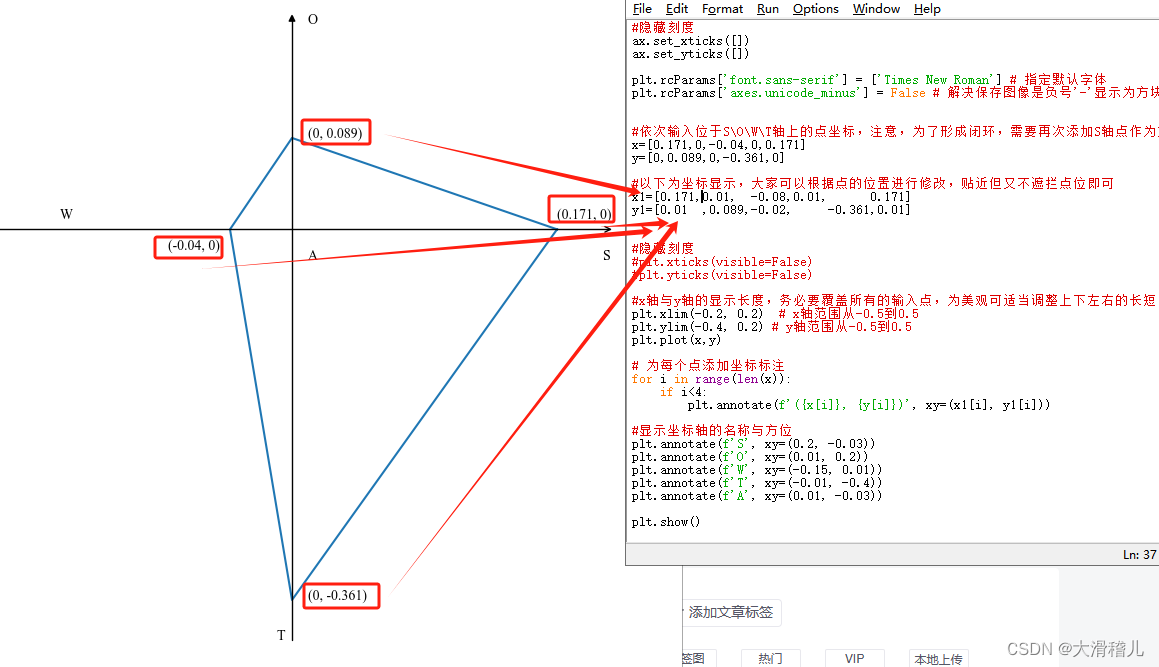
如何利用python画出AHP-SWOT的战略四边形(四象限图)
在企业或产业发展的相关论文分析中,常用到AHP-SWOT法进行定量分析,形成判断矩阵后,如何构造整洁的战略四边形是分析的最后一个环节,本文现将相关代码发布如下: import mpl_toolkits.axisartist as axisartist import …...

适用于智慧城市、智慧文旅等在线场景的轻量级3D数字人引擎MyAvatar简介
本人研发的国内首个纯面向web应用和小程序的轻量级3D虚拟人引擎MyAvatar。 功能简述 支持3D模型定制(写实或卡通风格均可,人物模型需实现绑定和变形)动画可以内置于模型中,也可以单独以glb或fbx格式导出并动态加载支持readyplay…...
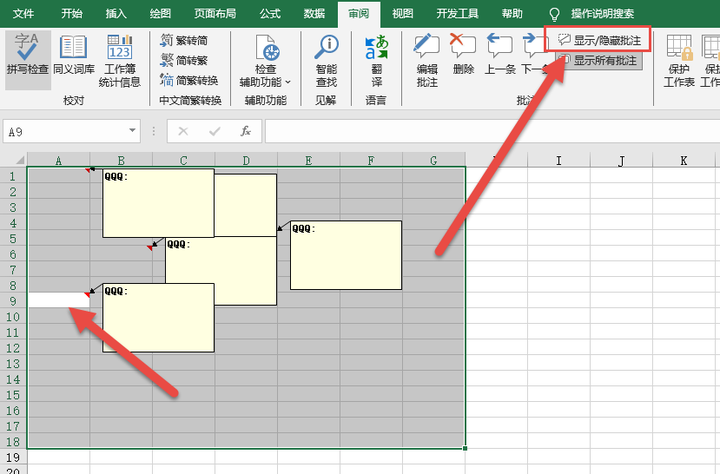
Excel显示/隐藏批注按钮为什么是灰色?
在excel中,经常使用批注来加强数据信息的提示,有时候会把很多的批注显示出来,但是再想将它们隐藏起来,全选工作表后,“显示/隐藏批注”按钮是灰色的,不可用。 二、可操作方法 批注在excel、WPS表格中都是按…...

ArtTS系统能力-通知的学习(3.1)
上篇回顾: ArtTS语言基础类库-容器类库内容的学习(2.10.2) 本篇内容: ArtTS系统能力-通知的学习(3.1) 一、 知识储备 1. 基础类型通知 按内容分成四类: 类型描述NOTIFICATION_CONTENT_BASIC_TEXT普通文…...
—— public_road_planner)
Apollo9.0 PNC源码学习之Planning模块(三)—— public_road_planner
前面文章: (1)Apollo9.0 PNC源码学习之Planning模块(一)—— 规划概览 (2)Apollo9.0 PNC源码学习之Planning模块(二)—— planning_component 1 planning_interface_base 规划接口基类: planning\planning_interface_base\planner_base\planner.h #pragma once#in…...

【Elasticsearch】linux使用supervisor常驻Elasticsearch,centos6.10安装 supervisor
背景: linux服务器,CentOS 6操作系统,默认版本python2.6.6,避免安装过多的依赖不升级python 在网上查的资料python2.6.6兼容supervisor版本 3.1.3 安装supervisor 手动在python官网下载supervisor,并上传到服务器 下…...

推荐系统三十六式学习笔记:原理篇.模型融合14|一网打尽协同过滤、矩阵分解和线性模型
目录 从特征组合说起FM模型1.原理2.模型训练3.预测阶段4.一网打尽其他模型5.FFM 总结 在上一篇文章中,我们讲到了使用逻辑回归和梯度提升决策树组合的模型融合办法,用于CTR预估,给这个组合起了个名字,叫“辑度组合”。这对组合中&…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...
