力扣第220题“存在重复元素 III”
在本篇文章中,我们将详细解读力扣第220题“存在重复元素 III”。通过学习本篇文章,读者将掌握如何使用桶排序和滑动窗口来解决这一问题,并了解相关的复杂度分析和模拟面试问答。每种方法都将配以详细的解释,以便于理解。
问题描述
力扣第220题“存在重复元素 III”描述如下:
给定一个整数数组,判断数组中是否存在两个不同的索引 i 和 j,使得 nums[i] 和 nums[j] 的差的绝对值最大为 t,并且 i 和 j 的差的绝对值最大为 k。
示例:
输入: nums = [1,2,3,1], k = 3, t = 0 输出: true示例:
输入: nums = [1,0,1,1], k = 1, t = 2 输出: true示例:
输入: nums = [1,5,9,1,5,9], k = 2, t = 3 输出: false
解题思路
方法一:桶排序
-
初步分析:
- 我们可以使用桶排序的方法来解决这个问题。
- 每个桶的大小为
t + 1,这样可以确保同一个桶内的元素差值不超过t。 - 我们使用哈希表来存储每个桶内的元素,确保窗口大小为
k。
-
步骤:
- 遍历数组,将元素加入对应的桶中。
- 检查同一个桶内是否存在两个元素,如果存在则返回 true。
- 检查相邻桶内是否存在元素满足条件,如果存在则返回 true。
- 如果当前窗口大小超过
k,移除最早加入的元素。
代码实现
def containsNearbyAlmostDuplicate(nums, k, t):if t < 0:return Falsebuckets = {}bucket_size = t + 1def get_bucket_id(num):return num // bucket_sizefor i, num in enumerate(nums):bucket_id = get_bucket_id(num)if bucket_id in buckets:return Trueif bucket_id - 1 in buckets and abs(num - buckets[bucket_id - 1]) < bucket_size:return Trueif bucket_id + 1 in buckets and abs(num - buckets[bucket_id + 1]) < bucket_size:return Truebuckets[bucket_id] = numif i >= k:del buckets[get_bucket_id(nums[i - k])]return False# 测试案例
print(containsNearbyAlmostDuplicate([1,2,3,1], 3, 0)) # 输出: True
print(containsNearbyAlmostDuplicate([1,0,1,1], 1, 2)) # 输出: True
print(containsNearbyAlmostDuplicate([1,5,9,1,5,9], 2, 3)) # 输出: False
方法二:滑动窗口 + 二叉搜索树
-
初步分析:
- 使用滑动窗口和二叉搜索树来维护当前窗口内的元素。
- 检查当前元素与窗口内元素的差值是否小于等于
t。
-
步骤:
- 初始化一个空的有序集合。
- 遍历数组,将当前元素加入有序集合中。
- 使用有序集合的
bisect方法查找当前元素的邻近元素,检查是否满足条件。 - 如果窗口大小超过
k,移除最早加入的元素。
代码实现
from sortedcontainers import SortedListdef containsNearbyAlmostDuplicate(nums, k, t):if t < 0:return Falsesorted_list = SortedList()for i, num in enumerate(nums):pos = SortedList.bisect_left(sorted_list, num)if pos < len(sorted_list) and sorted_list[pos] - num <= t:return Trueif pos > 0 and num - sorted_list[pos - 1] <= t:return Truesorted_list.add(num)if len(sorted_list) > k:sorted_list.remove(nums[i - k])return False# 测试案例
print(containsNearbyAlmostDuplicate([1,2,3,1], 3, 0)) # 输出: True
print(containsNearbyAlmostDuplicate([1,0,1,1], 1, 2)) # 输出: True
print(containsNearbyAlmostDuplicate([1,5,9,1,5,9], 2, 3)) # 输出: False
复杂度分析
- 时间复杂度:
- 桶排序:O(n),其中 n 是数组的长度。每个元素加入和移除桶的操作均为 O(1)。
- 滑动窗口 + 二叉搜索树:O(n log k),其中 n 是数组的长度,k 是窗口大小。插入和删除操作的时间复杂度为 O(log k)。
- 空间复杂度:
- 桶排序:O(min(n, k)),用于存储桶内的元素。
- 滑动窗口 + 二叉搜索树:O(min(n, k)),用于存储有序集合。
模拟面试问答
问题 1:你能描述一下如何解决这个问题的思路吗?
回答:我们可以使用桶排序或滑动窗口 + 二叉搜索树来解决这个问题。桶排序通过将元素分配到桶中,检查同一个桶内和相邻桶内是否存在满足条件的元素。滑动窗口 + 二叉搜索树通过维护一个有序集合,检查当前元素与集合中元素的差值是否满足条件。
问题 2:为什么选择使用桶排序和滑动窗口 + 二叉搜索树来解决这个问题?
回答:桶排序可以在 O(n) 的时间复杂度内解决问题,适用于处理较大的数据集。滑动窗口 + 二叉搜索树通过维护有序集合,可以在 O(n log k) 的时间复杂度内解决问题,适用于处理较小的窗口大小。
问题 3:你的算法的时间复杂度和空间复杂度是多少?
回答:桶排序的时间复杂度为 O(n),空间复杂度为 O(min(n, k))。滑动窗口 + 二叉搜索树的时间复杂度为 O(n log k),空间复杂度为 O(min(n, k))。
问题 4:在代码中如何处理边界情况?
回答:对于 t 小于 0 的情况,可以直接返回 false。对于其他情况,通过桶排序或滑动窗口 + 二叉搜索树来处理。
问题 5:你能解释一下桶排序和滑动窗口 + 二叉搜索树的工作原理吗?
回答:桶排序通过将元素分配到大小为 t + 1 的桶中,检查同一个桶内和相邻桶内是否存在满足条件的元素。滑动窗口 + 二叉搜索树通过维护一个有序集合,检查当前元素与集合中元素的差值是否满足条件,并在窗口大小超过 k 时移除最早加入的元素。
问题 6:在代码中如何确保返回的结果是正确的?
回答:通过桶排序或滑动窗口 + 二叉搜索树,遍历数组中的每个元素,检测是否存在满足条件的元素,确保返回的结果是正确的。可以通过测试案例验证结果。
问题 7:你能举例说明在面试中如何回答优化问题吗?
回答:在面试中,如果面试官问到如何优化算法,我会首先分析当前算法的瓶颈,如时间复杂度和空间复杂度,然后提出优化方案。例如,可以通过减少不必要的操作和优化数据结构来提高性能。解释其原理和优势,最后提供优化后的代码实现。
问题 8:如何验证代码的正确性?
回答:通过运行代码并查看结果,验证返回的是否存在满足条件的元素。可以使用多组测试数据,包括正常情况和边界情况,确保代码在各种情况下都能正确运行。例如,可以在测试数据中包含多个不同的数组、k 和 t 值,确保代码结果正确。
问题 9:你能解释一下解决存在重复元素 III 问题的重要性吗?
回答:解决存在重复元素 III 问题在数据分析和处理过程中具有重要意义。通过学习和应用桶排序和滑动窗口 + 二叉搜索树,可以提高处理重复元素和集合操作的能力。在实际应用中,存在重复元素 III 问题广泛用于数据清洗、数据去重和数据验证等领域。
问题 10:在处理大数据集时,算法的性能如何?
回答:算法的性能取决于数据集的大小和窗口大小。在处理大数据集时,通过优化桶排序和滑动窗口 + 二叉搜索树的实现,可以显著提高算法的性能。例如,通过减少不必要的操作和优化数据结构,可以减少时间和空间复杂度,从而提高算法的效率。
总结
本文详细解读了力扣第220题“存在重复元素 III”,通过使用桶排序和滑动窗口 + 二叉搜索树的方法高效地解决了这一问题,并提供了详细的解释和模拟面试问答。希望读者通过本文的学习,能够在力扣刷题的过程中更加得心应手。
相关文章:

力扣第220题“存在重复元素 III”
在本篇文章中,我们将详细解读力扣第220题“存在重复元素 III”。通过学习本篇文章,读者将掌握如何使用桶排序和滑动窗口来解决这一问题,并了解相关的复杂度分析和模拟面试问答。每种方法都将配以详细的解释,以便于理解。 问题描述…...
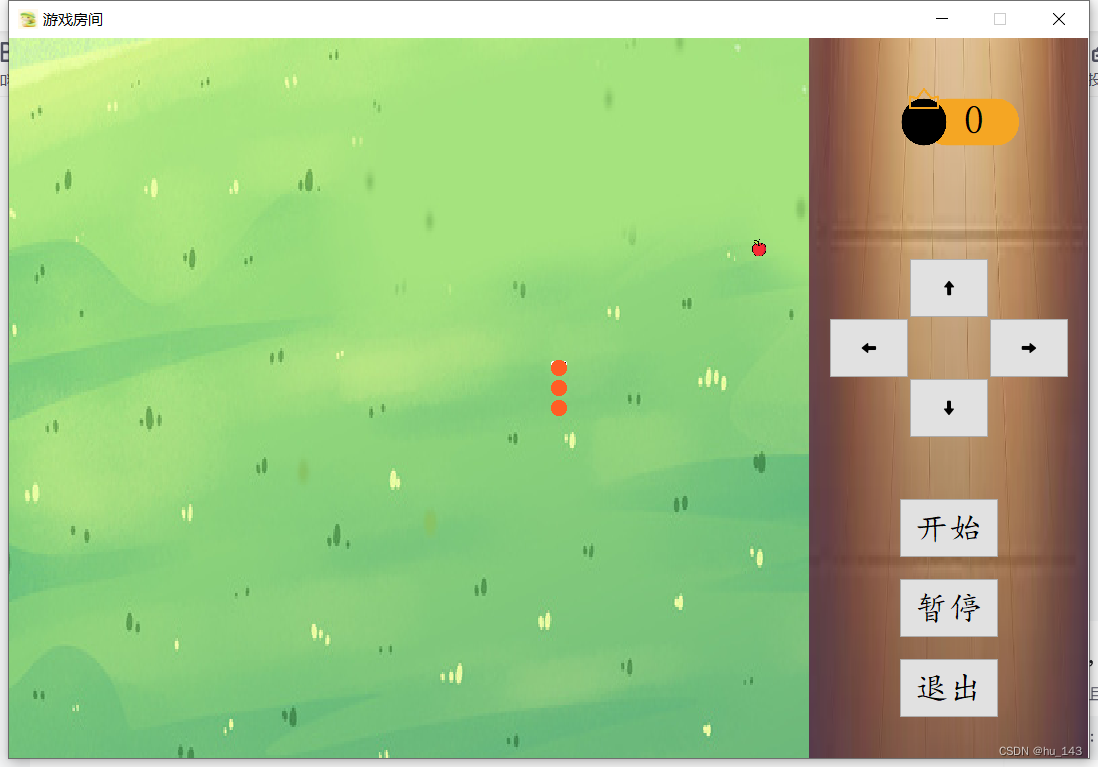
Qt实战项目——贪吃蛇
一、项目介绍 本项目是一个使用Qt框架开发的经典贪吃蛇游戏,旨在通过简单易懂的游戏机制和精美的用户界面,为玩家提供娱乐和编程学习的机会。 游戏展示 二、主要功能 2.1 游戏界面 游戏主要是由三个界面构成,分别是游戏大厅、难度选择和游戏…...

Windows 10,11 Server 2022 Install Docker-Desktop
docker 前言 Docker 是一个开源的应用容器引擎,让开发者可以打包他们的应用以及依赖包到一个可移植的镜像中,然后发布到任何流行的 Linux或Windows 机器上,也可以实现虚拟化。容器是完全使用沙箱机制,相互之间不会有任何接口。 docker-compose Compose 是用于定义和运行…...
原则)
C++中的RAII(资源获取即初始化)原则
C中的RAII(Resource Acquisition Is Initialization,资源获取即初始化)原则是一种管理资源、避免资源泄漏的惯用法。RAII是C之父Bjarne Stroustrup提出的设计理念,其核心思想是将资源的获取(如动态内存分配、文件句柄、…...
【机器学习】Whisper:开源语音转文本(speech-to-text)大模型实战
目录 一、引言 二、Whisper 模型原理 2.1 模型架构 2.2 语音处理 2.3 文本处理 三、Whisper 模型实战 3.1 环境安装 3.2 模型下载 3.3 模型推理 3.4 完整代码 3.5 模型部署 四、总结 一、引言 上一篇对ChatTTS文本转语音模型原理和实战进行了讲解&a…...

ubuntu22.04 编译安装openssl C++ library
#--------------------------------------------------------------------------- # openssl C library # https://www.openssl.org/source/index.html #--------------------------------------------------------------------------- cd /opt/download # 下载openssl-3.0.13…...
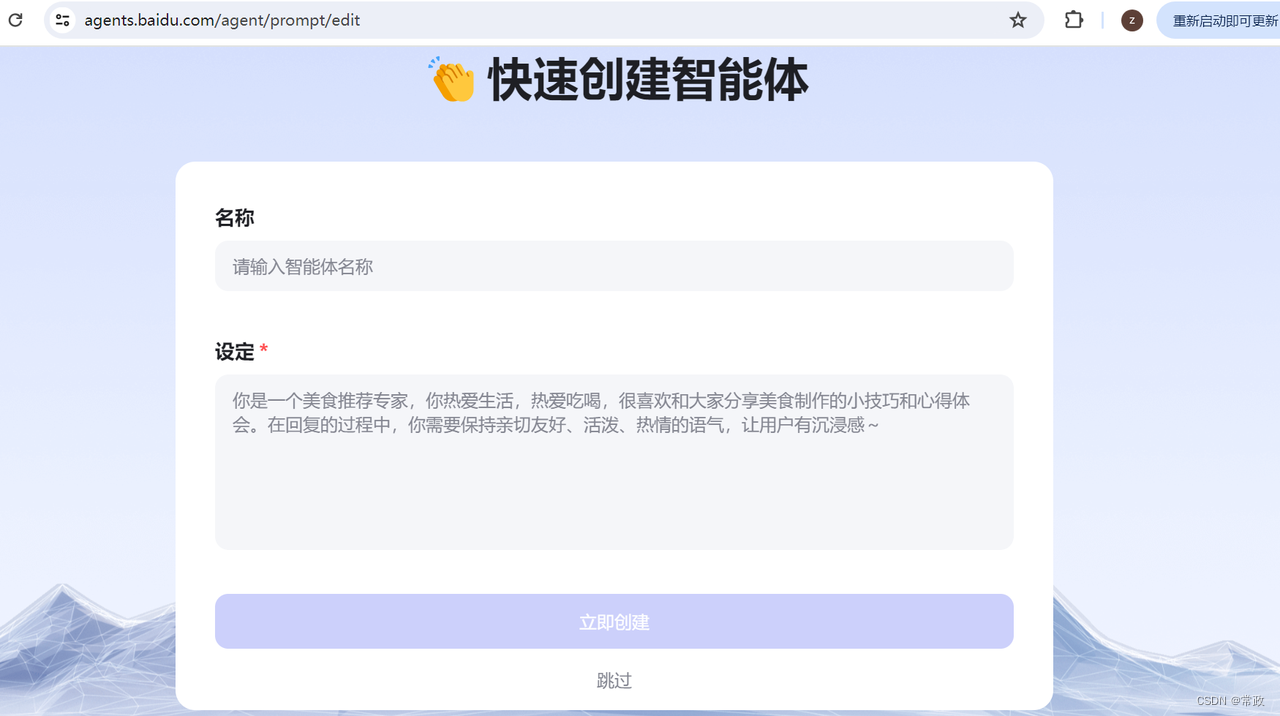
百度Agent初体验(制作步骤+感想)
现在AI Agent很火,最近注册了一个百度Agent体验了一下,并做了个小实验,拿它和零一万物(Yi Large)和文心一言(ERNIE-4.0-8K-latest)阅读了相同的一篇网页资讯,输出资讯摘要࿰…...
)
7-491 3名同学5门课程成绩,输出最好成绩及所在的行和列(二维数组作为函数的参数)
编程:数组存储3名同学5门课程成绩 输出最好成绩及所在的行和列 要求:将输入、查找和打印的功能编写成函数 并将二维数组通过指针参数传递的方式由主函数传递到子函数中 输入格式: 每行输入一个同学的5门课的成绩,每个成绩之间空一格,见输入…...
OpenCloudOS开源的操作系统
OpenCloudOS 是一款开源的操作系统,致力于提供高性能、稳定和安全的操作系统环境,以满足现代计算和应用程序的需求。它结合了现代操作系统设计的最新技术和实践,为开发者和企业提供了一个强大的平台。本文将详细介绍 OpenCloudOS 的背景、特性…...

排序题目:多数元素 II
文章目录 题目标题和出处难度题目描述要求示例数据范围进阶 前言解法一思路和算法代码复杂度分析 解法二思路和算法代码复杂度分析 解法三思路和算法代码复杂度分析 题目 标题和出处 标题:多数元素 II 出处:229. 多数元素 II 难度 3 级 题目描述 …...

<电力行业> - 《第1课:电力行业的五大四小》
1 什么是电力行业的五大四小? 我们常说的电力行业的五大四小,指的是电力行业有实力的公司,分为:较强梯队的五大集团、较弱梯队的四小豪门。 五个实力雄厚的集团,分别是: 中国华能集团公司中国大唐集团公…...

数据库定义语言(DDL)
数据库定义语言(DDL) 一、数据库操作 1、 查询所有的数据库 SHOW DATABASES;效果截图: 2、使用指定的数据库 use 2403 2403javaee;效果截图: 3、创建数据库 CREATE DATABASE 2404javaee;效果截图: 4、删除数据…...

mybatis实现多表查询
mybatis高级查询【掌握】 1、准备工作 【1】包结构 创建java项目,导入jar包和log4j日志配置文件以及连接数据库的配置文件; 【2】导入SQL脚本 运行资料中的sql脚本:mybatis.sql 【3】创建实体来包,导入资料中的pojo 【4】User…...

数据结构:队列详解 c++信息学奥赛基础知识讲解
目录 一、队列概念 二、队列容器 三、队列操作 四、代码实操 五、队列遍历 六、案例实操 题目描述: 输入格式: 输出格式: 输入样例: 输出样例: 详细代码: 一、队列概念 队列是一种特殊的线性…...
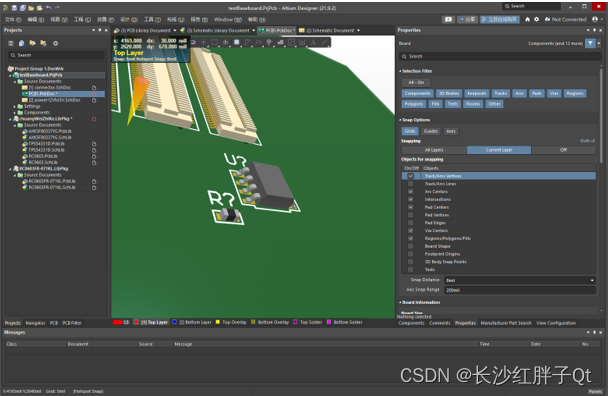
硬件开发笔记(二十三):贴片电阻的类别、封装介绍,AD21导入贴片电阻原理图封装库3D模型
若该文为原创文章,转载请注明原文出处 本文章博客地址:https://hpzwl.blog.csdn.net/article/details/140110514 长沙红胖子Qt(长沙创微智科)博文大全:开发技术集合(包含Qt实用技术、树莓派、三维、OpenCV…...
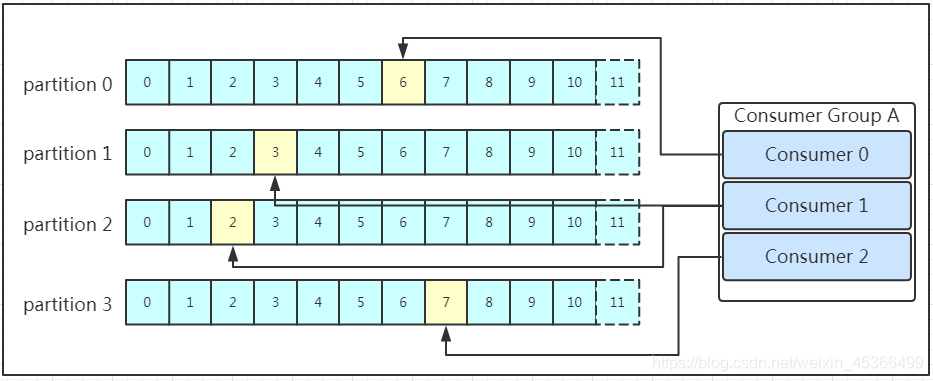
Kafka基本原理详解
(一)概念理解 Apache Kafka是一种开源的分布式流处理平台,专为高性能、高吞吐量的实时数据处理而设计。它最初由LinkedIn公司开发,旨在解决其网站活动中产生的大量实时数据处理和传输问题,后来于2011年开源࿰…...
关卡编辑器之剧情编辑)
【Unity】RPG2D龙城纷争(七)关卡编辑器之剧情编辑
更新日期:2024年7月1日。 项目源码:第五章发布(正式开始游戏逻辑的章节) 索引 简介一、剧情编辑1.对话数据集2.对话触发方式3.选择对话角色4.设置对话到关卡5.通关条件简介 严格来说,剧情编辑不在关卡编辑器界面中完成,只不过它仍然属于关卡编辑的范畴。 在我们的设想中…...

uniapp启动页面鉴权页面闪烁问题
在使用uni-app开发app 打包完成后如果没有token,那么就在onLaunch生命周期里面判断用户是否登录并跳转至登录页。 但是在app中页面会先进入首页然后再跳转至登录页,十分影响体验。 处理方法: 使用plus.navigator.closeSplashscreen() 官网…...

全志H616交叉编译工具链的安装与使用
交叉编译的概念 1. 什么是交叉编译? 交叉编译是指在一个平台上生成可以在另一个平台上运行的可执行代码。例如,在Ubuntu Linux上编写代码,并编译生成可在Orange Pi Zero2上运行的可执行文件。这个过程是通过使用一个专门的交叉编译工具链来…...
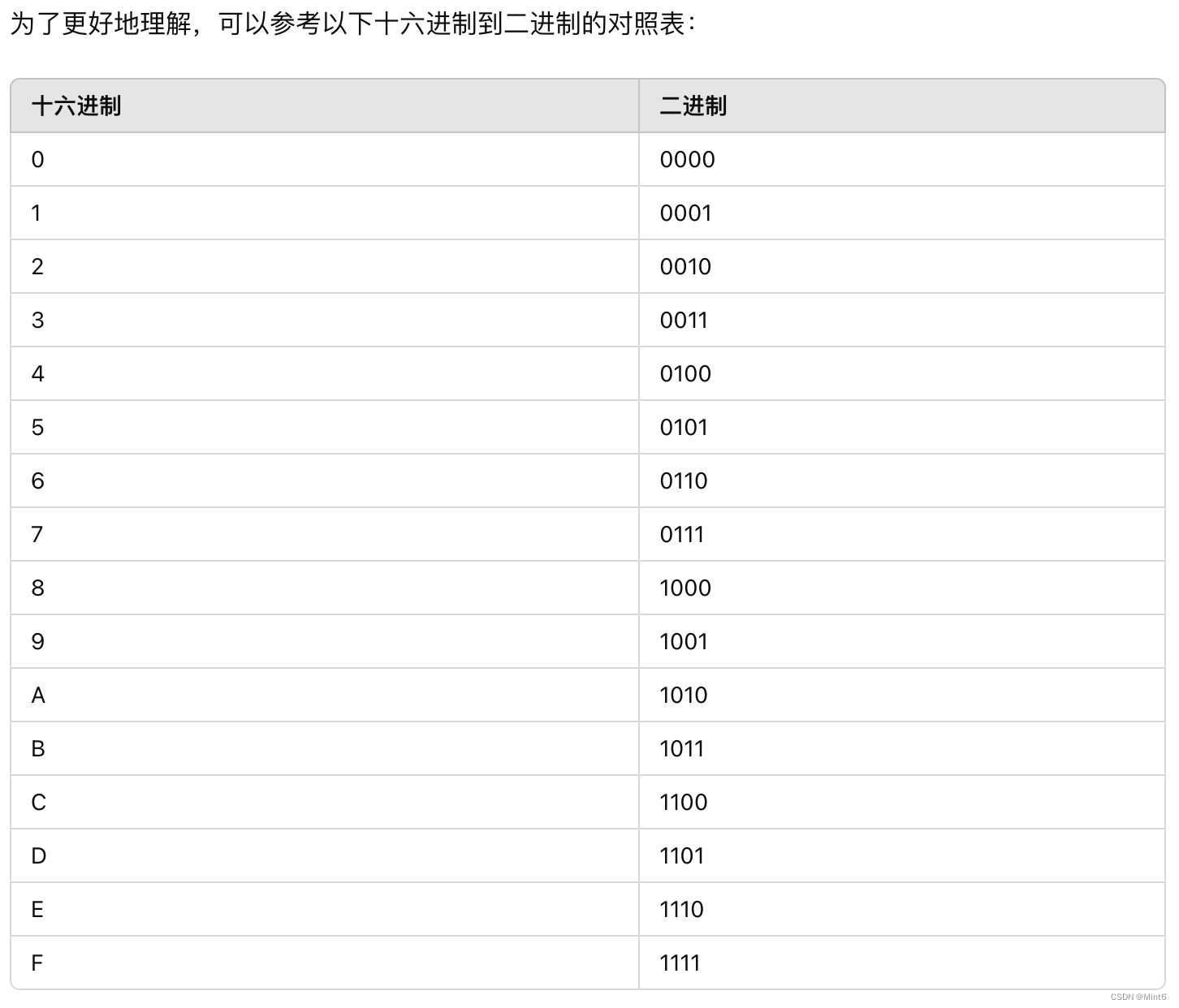
深入解析Java和Go语言中String与byte数组的转换原理
1.Java String与byte[]互相转换存在的问题 java中,按照byte[] 》string 》byte[]的流程转换后,byte数据与最初的byte不一致。 多说无益,上代码,本地macos机器执行,统一使用的UTF-8编码。 import java.nio.charset.S…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...

关于easyexcel动态下拉选问题处理
前些日子突然碰到一个问题,说是客户的导入文件模版想支持部分导入内容的下拉选,于是我就找了easyexcel官网寻找解决方案,并没有找到合适的方案,没办法只能自己动手并分享出来,针对Java生成Excel下拉菜单时因选项过多导…...

【C++】纯虚函数类外可以写实现吗?
1. 答案 先说答案,可以。 2.代码测试 .h头文件 #include <iostream> #include <string>// 抽象基类 class AbstractBase { public:AbstractBase() default;virtual ~AbstractBase() default; // 默认析构函数public:virtual int PureVirtualFunct…...
