【二叉树广度优先遍历和深度优先遍历】
文章目录
- 一、二叉树的深度优先遍历
- 0.建立一棵树
- 1. 前序遍历
- 2.中序遍历
- 3. 后序遍历
- 二、二叉树的广度优先遍历
- 层序遍历
- 三、有关二叉树练习
一、二叉树的深度优先遍历
学习二叉树结构,最简单的方式就是遍历。
所谓二叉树遍历(Traversal)是按照某种特定的规则,依次对二叉
树中的节点进行相应的操作,并且每个节点只操作一次。访问结点所做的操作依赖于具体的应用问题。
遍历是二叉树上最重要的运算之一,也是二叉树上进行其它运算的基础。
按照规则,二叉树的遍历有:前序/中序/后序的递归结构遍历:
0.建立一棵树
typedef char BTDataType;typedef struct BinaryTreeNode
{BTDataType data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;}BTNode;int main()
{BTNode* A = (BTNode*)malloc(sizeof(BTNode));A->data = 'A';A->left = NULL;A->right = NULL;BTNode* B = (BTNode*)malloc(sizeof(BTNode));B->data = 'B';B->left = NULL;B->right = NULL;BTNode* C = (BTNode*)malloc(sizeof(BTNode));C->data = 'C';C->left = NULL;C->right = NULL;BTNode* D = (BTNode*)malloc(sizeof(BTNode));D->data = 'D';D->left = NULL;D->right = NULL;BTNode* E = (BTNode*)malloc(sizeof(BTNode));E->data = 'E';E->left = NULL;E->right = NULL;A->left = B;A->right =C;B->left = D;B->right = E;return 0;
}
结果如下:

1. 前序遍历
访问根结点的操作发生在遍历其左右子树之前。
先访问根节点,再到左子节点,然后到右子节点。
根->左->右

//后序遍历
void PrevOrder(BTNode* root)
{if (root == NULL){return;}printf("%c ", root->data);PrevOrder(root->left);PrevOrder(root->right);
}

2.中序遍历
- 中序遍历(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中(间)。
先访问左子树,再访问根,再到右子树
左–>根–>右

由于NULL不打印出来,故结果为 D->B->E->A->C
代码如下:
//中序遍历
void InOrder(BTNode* root)
{if (root == NULL){return;}InOrder(root->left);printf("%c ", root->data);InOrder(root->right);
}
代码分析:

3. 后序遍历
- 后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。
先访问左子节点,再访问右子节点,最后访问根。
左–>右–>根
分析结果如下
打印结果为: D E B C A
代码如下:
//后续遍历
void PostOrder(BTNode* root)
{if (!root){return;}PostOrder(root->left);PostOrder(root->right);printf("%c ", root->data);
}
代码分析如下:

二叉树的前序,中序,后序遍历结果如下:

二、二叉树的广度优先遍历
层序遍历
层序遍历:除了先序遍历、中序遍历、后序遍历外,还可以对二叉树进行层序遍历。设二叉树的根节点所在层数为1
层序遍历就是从所在二叉树的根节点出发,首先访问第一层的树根节点,然后从左到右访问第2层上的节点,接着是第三层的节点
以此类推,自上而下,自左至右逐层访问树的结点的过程就是层序遍历。
层序遍历就是一层一层地访问,先访问第一层, 再访问第二层。
核心思想是上一层出去带下一层进来
实现的过程不使用递归实现,使用队列实现:
借助队列先进先出的特点

队列源代码:
typedef struct BinaryTreeNode* QDataType;typedef struct QueueNode
{QDataType data;struct QueueNode* next;
}QNode;typedef struct Queue
{QNode* head;QNode* tail;int size;
}Queue;void QueueInit(Queue* pq)
{assert(pq);pq->head = NULL;pq->tail = NULL;pq->size = 0;
}void QueueDestroy(Queue* pq)
{assert(pq);QNode* cur = pq->head;while (cur){QNode* del = cur;cur = cur->next;free(del);//del = NULL;}pq->head = pq->tail = NULL;pq->size = 0;
}void QueuePush(Queue* pq, QDataType x)
{assert(pq);QNode* newnode = (QNode*)malloc(sizeof(QNode));if (newnode == NULL){perror("malloc fail");exit(-1);}newnode->data = x;newnode->next = NULL;if (pq->tail == NULL){pq->head = pq->tail = newnode;}else{pq->tail->next = newnode;pq->tail = newnode;}pq->size++;
}void QueuePop(Queue* pq)
{assert(pq);assert(!QueueEmpty(pq));if (pq->head->next == NULL){free(pq->head);pq->head = pq->tail = NULL;}else{QNode* del = pq->head;pq->head = pq->head->next;free(del);}pq->size--;
}QDataType QueueFront(Queue* pq)
{assert(pq);assert(!QueueEmpty(pq));return pq->head->data;
}bool QueueEmpty(Queue* pq)
{assert(pq);return pq->head == NULL && pq->tail == NULL;
}实现层序遍历过程中二叉树借助队列源代码:
//借助队列的先进先出来实现层级递进
void LevelOrder(BTNode* root)
{//核心思路,上一层出的时候带下一层Queue q;QueueInit(&q);if (root){QueuePush(&q, root);}while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);printf("%c ", front->data);//访问下一层if (front->left){QueuePush(&q, front->left);}if (front->right){QueuePush(&q, front->right);}}printf("\n");QueueDestroy(&q);
}
三、有关二叉树练习
1.某完全二叉树按层次输出(同一层从左到右)的序列为 ABCDEFGH 。
该完全二叉树的前序序列为( )
A ABDHECFG
B ABCDEFGH
C HDBEAFCG
D HDEBFGCA
解析:
已知该树为完全二叉树,第一层只有一个节点,第二层有2个节点,第三层有4个节点…
容易知道该完全二叉树的高度是4,还原可得:
根据前序序列遍历,先根,再左子节点,再右子节点,选A
2.二叉树的先序遍历和中序遍历如下:先序遍历:EFHIGJK;中序遍历:HFIEJKG.则二叉树根结点为()
A E
B F
C G
D H
解析:由二叉树的前序遍历可知,根节点为E。
此时已经得出答案,但我想还原这棵树
由中序遍历可知:E是根节点,那么E左边的所有节点为HFI,右边的所有节点为JKG
由前序遍历可知,E到F,说明F是E的左子节点,由中序遍历,H到F,说名H是F的左子节点。到这里可以还原二叉树的左半部分了,右半部分同理。
3.设一课二叉树的中序遍历序列:badce,后序遍历序列:bdeca,
则二叉树前序遍历序列为____。
A adbce
B decab
C debac
D abcde
解析:
由二叉树的后序遍历可知根节点为a。
由中序序列可知a的左子节点只有b,右子节点右dce
又由后序遍历往前推,可知c是a的右子节点
到这里已经可以推出整棵树了
所以该树的前序序列为abcde,选D
4.某二叉树的后序遍历序列与中序遍历序列相同,均为 ABCDEF ,
则按层次输出(同一层从左到右)的序列为
A FEDCBA
B CBAFED
C DEFCBA
D ABCDEF
解析:
由二叉树的后序遍历可知,根节点为F,由中序遍历可知,根节点F无右子节点。
F的左节点有ABCDE
又因为前序和中序都相同,那么只有一种情况:
所以答案选A
相关文章:

【二叉树广度优先遍历和深度优先遍历】
文章目录一、二叉树的深度优先遍历0.建立一棵树1. 前序遍历2.中序遍历3. 后序遍历二、二叉树的广度优先遍历层序遍历三、有关二叉树练习一、二叉树的深度优先遍历 学习二叉树结构,最简单的方式就是遍历。 所谓二叉树遍历(Traversal)是按照某种特定的规则ÿ…...
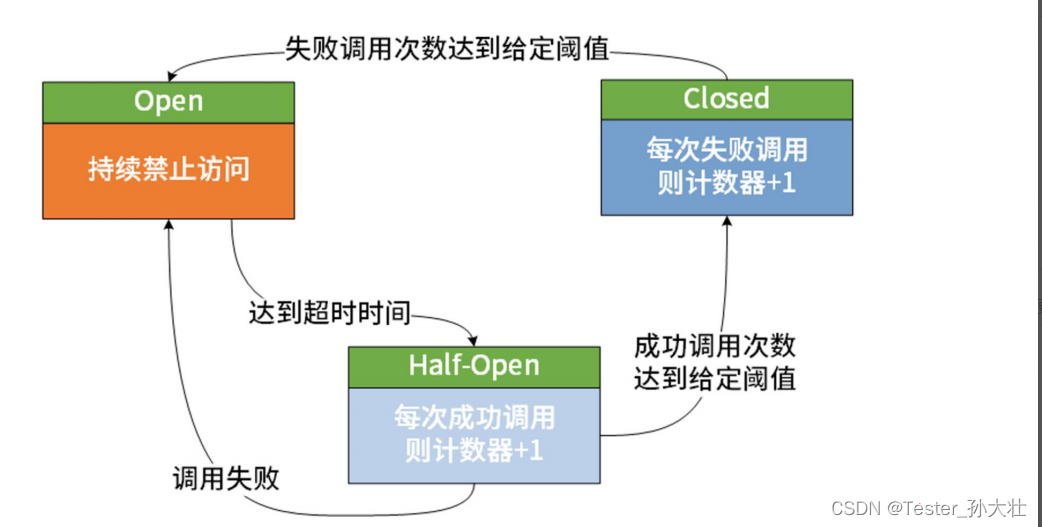
Spring Cloud微服务架构必备技术
单体架构 单体架构,也叫单体应用架构,是一个传统的软件架构模式。单体架构是指将应用程序的所有组件部署到一个单一的应用程序中,并统一进行部署、维护和扩展。在单体架构中,应用程序的所有功能都在同一个进程中运行,…...
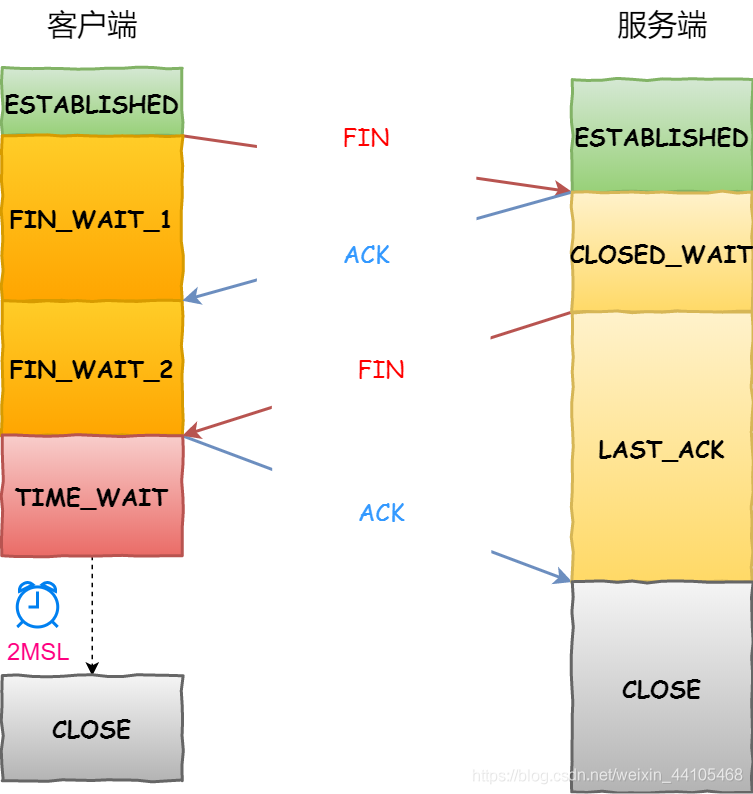
TCP三次握手与四次挥手(一次明白)
TCP基本信息 默认端口号:80 LINUX中TIME_WAIT的默认时间是30s TCP三次握手 三次握手过程:每行代表发起握手到另一方刚刚收到数据包时的状态 客户端服务端客户端状态服务端状态握手前CLOSELISTEN客户端发送带有SYN标志的数据包到服务端一次握手SYN_SENDLISTEN二次握手服务端发送…...

pyside6@Mouse events实例@QApplication重叠导致的报错@keyboardInterrupt
文章目录报错内容鼠标事件演示报错内容 在pyside图形界面应用程序开发过程中,通常只允许运行一个实例 假设您重复执行程序A,那么可能会导致一些意向不到的错误并且,从python反馈的信息不容易判断错误的真正来源 鼠标事件演示 下面是一段演示pyside6的鼠标事件mouseEvent对象…...

订单30分钟未支付自动取消怎么实现?
目录了解需求方案 1:数据库轮询方案 2:JDK 的延迟队列方案 3:时间轮算法方案 4:redis 缓存方案 5:使用消息队列了解需求在开发中,往往会遇到一些关于延时任务的需求。例如生成订单 30 分钟未支付࿰…...

< 开源项目框架:推荐几个开箱即用的开源管理系统 - 让开发不再复杂 >
文章目录👉 SCUI Admin 中后台前端解决方案👉 Vue .NetCore 前后端分离的快速发开框架👉 next-admin 适配移动端、pc的后台模板👉 django-vue-admin-pro 快速开发平台👉 Admin.NET 通用管理平台👉 RuoYi 若…...

内网渗透-基础环境
解决依赖,scope安装 打开要给cmd powershell 打开远程 Set-ExecutionPolicy RemoteSigned -scope CurrentUser; 我试了好多装这东西还是得科学上网,不然不好用 iwr -useb get.scoop.sh | iex 查看下载过的软件 安装sudo 安装git 这里一定要配置bu…...

Go语言学习的第一天(对于Go学习的认识和工具选择及环境搭建)
首先学习一门新的语言,我们要知道这门语言可以帮助我们做些什么?为什么我们要学习这门语言?就小wei而言学习这门语言是为了区块链,因为自身是php出身,因为php的一些特性只能通过一些算法模拟的做一个虚拟链,…...

C和C++到底有什么关系
C++ 读作”C加加“,是”C Plus Plus“的简称。顾名思义,C++是在C的基础上增加新特性,玩出了新花样,所以叫”C Plus Plus“,就像 iPhone 6S 和 iPhone 6、Win10 和 Win7 的关系。 C语言是1972年由美国贝尔实验室研制成功的,在当时算是高级语言,它的很多新特性都让汇编程序…...
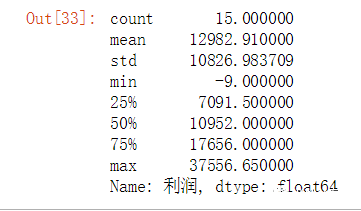
14个Python处理Excel的常用操作,非常好用
自从学了Python后就逼迫用Python来处理Excel,所有操作用Python实现。目的是巩固Python,与增强数据处理能力。 这也是我写这篇文章的初衷。废话不说了,直接进入正题。 数据是网上找到的销售数据,长这样: 一、关联公式:…...

async/await 用法
1. 什么是 async/await async/await 是 ES8(ECMAScript 2017)引入的新语法,用来简化 Promise 异步操作。在 async/await 出 现之前,开发者只能通过链式 .then() 的方式处理 Promise 异步操作。示例代码如下: import …...
好意外,发现永久免费使用的云服务器
原因就不说了,说一下过程,在百度搜pythonIDE的时候,发现了一个网站 https://lightly.teamcode.com/https://lightly.teamcode.com/ 就是这个网站,看见这个免费试用,一开始觉得没什么,在尝试使用的过程中发…...
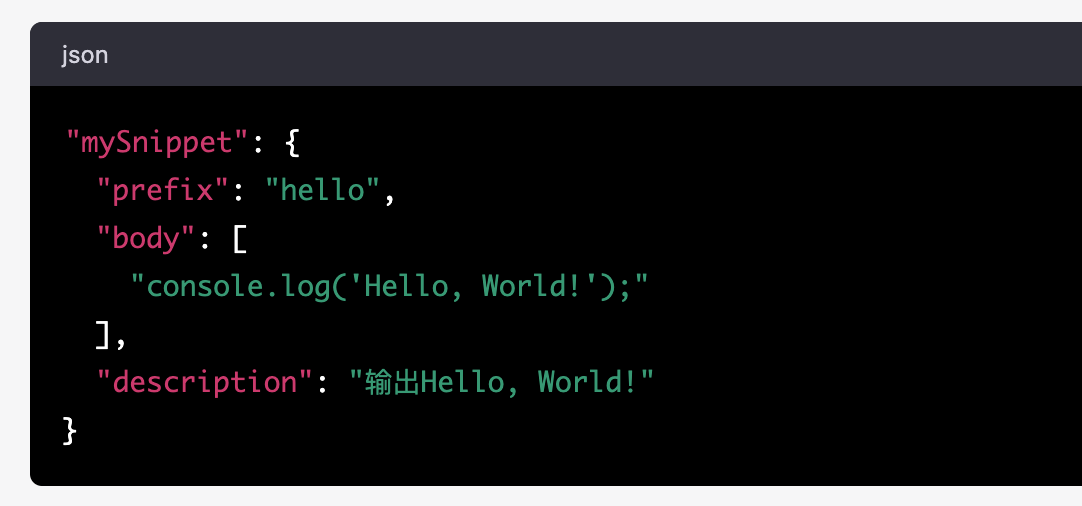
VSCode使用技巧,代码编写效率提升2倍以上!
VSCode是一款开源免费的跨平台文本编辑器,它的可扩展性和丰富的功能使得它成为了许多程序员的首选编辑器。在本文中,我将分享一些VSCode的使用技巧,帮助您更高效地使用它。 1. 插件 VSCode具有非常丰富的插件生态系统,通过安装插…...
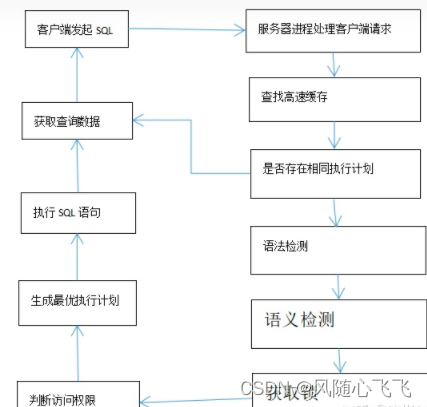
SQL执行过程详解
1 、用户在客户端执行 SQL 语句时,客户端把这条 SQL 语句发送给服务端,服务端的进程,会处理这条客户端的SQL语句。 2 、服务端进程收集到SQL信息后,会在进程全局区PGA 中分配所需内存,存储相关的登录信息等。 3 、客…...
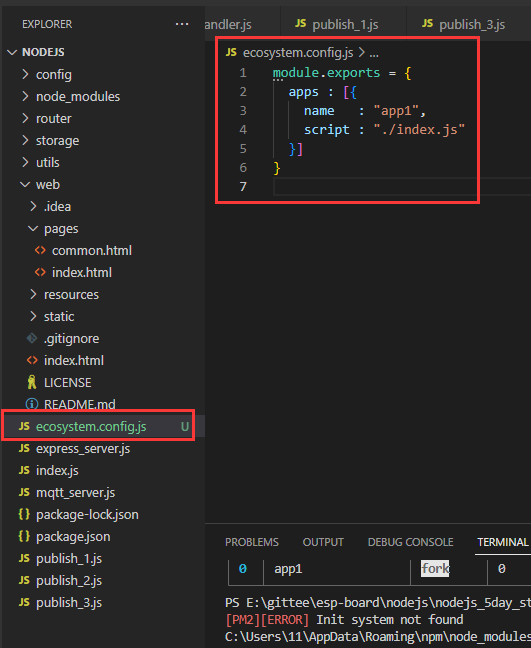
【物联网NodeJs-5天学习】第四天存储篇⑤ ——PM2,node.js应用进程管理器
【NodeJs-5天学习】第四天存储篇⑤ ——PM2,node.js应用进程管理器1. 前言2. 官方说明3. 安装PM24. PM2常用命令4.1 启动命令4.2 重新启动命令4.3 热重载命令4.4 停止命令4.5 删除命令4.6 查看进程运行状态4.4 显示某一个进程的具体信息4.8 显示日志信息4.9 终端监控…...

【C++学习】【STL】deque容器
dequeDouble Ended Queues(双向队列)deque和vector很相似,但是它允许在容器头部快速插入和删除(就像在尾部一样)。所耗费的时间复杂度也为常数阶O(1)。并且更重要的一点是,deque 容器中存储元素并不能保证所有元素都存储到连续的内…...

当 App 有了系统权限,真的可以为所欲为?
看到群里发了两篇文章,出于好奇,想看看这些个 App 在利用系统漏洞获取系统权限之后,都干了什么事,于是就有了这篇文章。由于准备仓促,有些 Code 没有仔细看,感兴趣的同学可以自己去研究研究,多多…...

vue3.js的介绍
一.vue.js简述 Vue是一套用于构建用户开源的MVVM结构的Javascript渐进式框架,尤雨溪在2015年10月27日发布了vue.js 1.0Eavangelion版本,在2016年9月30日发布了2.0Ghost in the Shell版本,目前项目由官方负责 vue的核心只关注图层࿰…...

【Three.js】shader特效 能量盾
shader特效之能量盾前言效果噪点图主要代码index.htmldepth-fs.jsdepth-vs.jsshield-fs.jsshield-vs.js相关项目前言 效果噪点图 为了可以自定义能量球的效果,这里使用外部加载来的噪点图做纹理,省去用代码写特效的过程。 主要代码 index.html <…...

【6000字长文】需求评审总是被怼?强烈推荐你试试这三招
前段时间和一个合作部门的产品新人沟通需求,结束的时候,他问了我一个问题,“你在产品新人阶段,最害怕做的事情是什么”? 我不假思索的回答说,“需求评审,是曾经最不想面对的环节,甚至在评审之前几个小时就开始心跳加速了。当然这也是产品修炼路上的必经之路,其实只要掌…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

【p2p、分布式,区块链笔记 MESH】Bluetooth蓝牙通信 BLE Mesh协议的拓扑结构 定向转发机制
目录 节点的功能承载层(GATT/Adv)局限性: 拓扑关系定向转发机制定向转发意义 CG 节点的功能 节点的功能由节点支持的特性和功能决定。所有节点都能够发送和接收网格消息。节点还可以选择支持一个或多个附加功能,如 Configuration …...

深度学习之模型压缩三驾马车:模型剪枝、模型量化、知识蒸馏
一、引言 在深度学习中,我们训练出的神经网络往往非常庞大(比如像 ResNet、YOLOv8、Vision Transformer),虽然精度很高,但“太重”了,运行起来很慢,占用内存大,不适合部署到手机、摄…...

【1】跨越技术栈鸿沟:字节跳动开源TRAE AI编程IDE的实战体验
2024年初,人工智能编程工具领域发生了一次静默的变革。当字节跳动宣布退出其TRAE项目(一款融合大型语言模型能力的云端AI编程IDE)时,技术社区曾短暂叹息。然而这一退场并非终点——通过开源社区的接力,TRAE在WayToAGI等…...

Python第七周作业
Python第七周作业 文章目录 Python第七周作业 1.使用open以只读模式打开文件data.txt,并逐行打印内容 2.使用pathlib模块获取当前脚本的绝对路径,并创建logs目录(若不存在) 3.递归遍历目录data,输出所有.csv文件的路径…...

CVE-2023-25194源码分析与漏洞复现(Kafka JNDI注入)
漏洞概述 漏洞名称:Apache Kafka Connect JNDI注入导致的远程代码执行漏洞 CVE编号:CVE-2023-25194 CVSS评分:8.8 影响版本:Apache Kafka 2.3.0 - 3.3.2 修复版本:≥ 3.4.0 漏洞类型:反序列化导致的远程代…...



