数据结构和算法,单链表的实现(kotlin版)
文章目录
- 数据结构和算法,单链表的实现(kotlin版)
- b站视频链接
- 1.定义接口,我们需要实现的方法
- 2.定义节点,表示每个链表节点。
- 3.push(e: E),链表尾部新增一个节点
- 4.size(): Int,返回链表的长度
- 5.getValue(index: Int): E?,获取列表的value值
- 6.insert(index: Int,e: E),从任意位置插入一个节点
- 7.remove(index: Int),任意位置删除一个节点
- 8.完整Demo
数据结构和算法,单链表的实现(kotlin版)
b站视频链接
单链表的实现–koltin版本
1.定义接口,我们需要实现的方法
interface LinkedListAction<E> {fun push(e: E)fun size(): Intfun getValue(index: Int): E?fun insert(index: Int,e: E)fun remove(index: Int)
}
2.定义节点,表示每个链表节点。
data class Node<E>(var next: Node<E>? = null, var value: E)
3.push(e: E),链表尾部新增一个节点
override fun push(e: E) {val newNode = Node(null, e)if (head != null) {
// val lastNode = node(len - 1)//O(1)时间复杂度last?.next = newNode} else {head = newNode}last = newNodelen++}
4.size(): Int,返回链表的长度
override fun size(): Int {return len}
5.getValue(index: Int): E?,获取列表的value值
override fun getValue(index: Int): E? {if (index < 0 || index >= len) {throw ArrayIndexOutOfBoundsException("数组越界.....")}return node(index)?.value}//找到对应index下标的节点。private fun node(index: Int): Node<E>? {var h = head//O(n)时间复杂度for (i in 0 until index) {h = h?.next}return h}
6.insert(index: Int,e: E),从任意位置插入一个节点
override fun insert(index: Int, e: E) {val newNode = Node(null, e)//考虑边界if (index == 0) {val h = headhead = newNodenewNode.next = h} else {//考虑最后一个位置val prev = node(index - 1)val next = prev?.nextprev?.next = newNodenewNode.next = next}len++}//找到对应index下标的节点。private fun node(index: Int): Node<E>? {var h = head//O(n)时间复杂度for (i in 0 until index) {h = h?.next}return h}
7.remove(index: Int),任意位置删除一个节点
override fun remove(index: Int) {if (index < 0 || index >= len) {throw ArrayIndexOutOfBoundsException("数组越界.....")}if (index == 0) {val h = headhead = h?.nexth?.next = null} else {val prev = node(index - 1)val current = prev?.nextprev?.next = current?.nextcurrent?.next = null}len--}//找到对应index下标的节点。private fun node(index: Int): Node<E>? {var h = head//O(n)时间复杂度for (i in 0 until index) {h = h?.next}return h}
8.完整Demo
package day1class LinkedList<E> : LinkedListAction<E> {//头指针private var head: Node<E>? = null//优化时间复杂度private var last: Node<E>? = null//集合的长度private var len = 0override fun push(e: E) {val newNode = Node(null, e)if (head != null) {
// val lastNode = node(len - 1)//O(1)时间复杂度last?.next = newNode} else {head = newNode}last = newNodelen++}//找到对应index下标的节点。private fun node(index: Int): Node<E>? {var h = head//O(n)时间复杂度for (i in 0 until index) {h = h?.next}return h}override fun size(): Int {return len}override fun getValue(index: Int): E? {if (index < 0 || index >= len) {throw ArrayIndexOutOfBoundsException("数组越界.....")}return node(index)?.value}override fun insert(index: Int, e: E) {val newNode = Node(null, e)//考虑边界if (index == 0) {val h = headhead = newNodenewNode.next = h} else {//考虑最后一个位置val prev = node(index - 1)val next = prev?.nextprev?.next = newNodenewNode.next = next}len++}override fun remove(index: Int) {if (index < 0 || index >= len) {throw ArrayIndexOutOfBoundsException("数组越界.....")}if (index == 0) {val h = headhead = h?.nexth?.next = null} else {val prev = node(index - 1)val current = prev?.nextprev?.next = current?.nextcurrent?.next = null}len--}}
相关文章:
)
数据结构和算法,单链表的实现(kotlin版)
文章目录 数据结构和算法,单链表的实现(kotlin版)b站视频链接1.定义接口,我们需要实现的方法2.定义节点,表示每个链表节点。3.push(e: E),链表尾部新增一个节点4.size(): Int,返回链表的长度5.getValue(index: Int): E…...

Jdk17是否有可能代替 Jdk8
JDK发展历史和开源 2006年SUN公司开源JDK,成立OpenJDK组织。2009年Oracle收购SUN,加快JDK发布周期。Oracle JDK与OpenJDK功能基本一致,但Oracle JDK提供更长时间的更新支持。 JDK版本特性 JDK11是长期支持版本(LTS)…...

oca和 ocp有什么区别
OCA(Oracle Certified Associate)和OCP(Oracle Certified Professional)在Oracle的认证体系中是两种不同级别的认证,它们之间存在明显的区别。以下是对两者区别的详细解释: 认证级别: OCA&…...

煤矿安全大模型:微调internlm2模型实现针对煤矿事故和煤矿安全知识的智能问答
煤矿安全大模型————矿途智护者 使用煤矿历史事故案例,事故处理报告、安全规程规章制度、技术文档、煤矿从业人员入职考试题库等数据,微调internlm2模型实现针对煤矿事故和煤矿安全知识的智能问答。 本项目简介: 近年来,国家对煤矿安全生产的重视程度不断提升。为了确…...

C++中的C++中的虚析构函数的作用和重要性
在C中,虚析构函数(virtual destructor)的作用和重要性主要体现在多态和继承的上下文中。了解这一点之前,我们先简要回顾一下多态和继承的基本概念。 继承与多态 继承:允许我们定义一个基类(也称为父类或超…...

机器学习 - 文本特征处理之 TF 和 IDF
TF(Term Frequency,词频)和IDF(Inverse Document Frequency,逆文档频率)是文本处理和信息检索中的两个重要概念,常用于计算一个词在文档中的重要性。下面是详细解释: TF(…...
因为自己淋过雨所以想给嵌入式撑把伞
在开始前刚好我有一些资料,是我根据网友给的问题精心整理了一份「嵌入式的资料从专业入门到高级教程」, 点个关注在评论区回复“888”之后私信回复“888”,全部无偿共享给大家!!!新手学嵌入式,…...

《C++20设计模式》中单例模式
文章目录 一、前言二、饿汉式1、实现 三、懒汉式1、实现 四、最后 一、前言 单例模式定义: 单例模式(Singleton Pattern)是一种创建型设计模式,其主要目的是确保一个类只有一个实例,并提供全局访问点来访问这个实例。…...
前端技术(说明篇)
Introduction ##编写内容:1.前端概念梳理 2.前端技术种类 3.前端学习方式 ##编写人:贾雯爽 ##最后更新时间:2024/07/01 Overview 最近在广州粤嵌进行实习,项目名称是”基于Node实现多人聊天室“,主要内容是对前端界…...
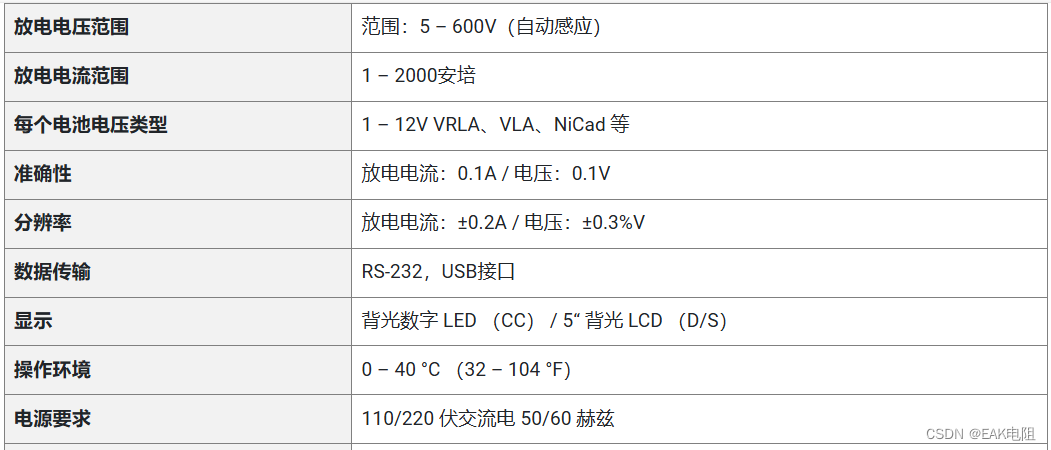
带电池监控功能的恒流直流负载组
EAK的交流和直流工业电池负载组测试仪对于测试和验证关键电力系统的能力至关重要,旨在实现最佳精度。作为一家客户至上的公司,我们继续尽我们所能应对供应链挑战,以提供出色的交货时间,大约是行业其他公司的一半。 交流负载组 我…...

关于Disruptor监听策略
Disruptor框架提供了多种等待策略,每种策略都有其适用的场景和特点。以下是这些策略的详细介绍及其适用场景: 1. BlockingWaitStrategy 特点: 使用锁和条件变量进行线程间通信,线程在等待时会进入阻塞状态,释放CPU资…...
)
大数据面试题之HBase(3)
HBase的预分区 HBase的热点问题 HBase的memstore冲刷条件 HBase的MVCC HBase的大合并与小合并,大合并是如何做的?为什么要大合并 既然HBase底层数据是存储在HDFS上,为什么不直接使用HDFS,而还要用HBase HBase和Phoenix的区别 HBase支…...

c#中赋值、浅拷贝和深拷贝
在 C# 编程中,深拷贝(Deep Copy)和浅拷贝(Shallow Copy)是用于复制对象的两种不同方式,它们在处理对象时有着重要的区别和适用场景。 浅拷贝(Shallow Copy) 浅拷贝是指创建一个新对…...

旧版st7789屏幕模块 没有CS引脚的天坑 已解决!!!
今天解决了天坑一个,大家可能有的人买的是st7789屏幕模块,240x240,1.3寸的 他标注的是老版,没有CS引脚,小崽子长这样: 这熊孩子用很多通用的驱动不吃,死活不显示,网上猛搜ÿ…...

激光粒度分析仪校准步骤详解:提升测量精度的秘诀
在材料科学、环境监测、医药研发等众多领域,激光粒度分析仪以其高精度、高效率的测量性能,成为了不可或缺的测试工具。然而,为了保持其测量结果的准确性和可靠性,定期校准是不可或缺的步骤。 接下来,佰德将为您详细介…...

独一无二的设计模式——单例模式(python实现)
1. 引言 大家好,今天我们来聊聊设计模式中的“独一无二”——单例模式。想象一下,我们在开发一个复杂的软件系统,需要一个全局唯一的配置管理器,或者一个统一的日志记录器;如果每次使用这些功能都要创建新的实例&…...
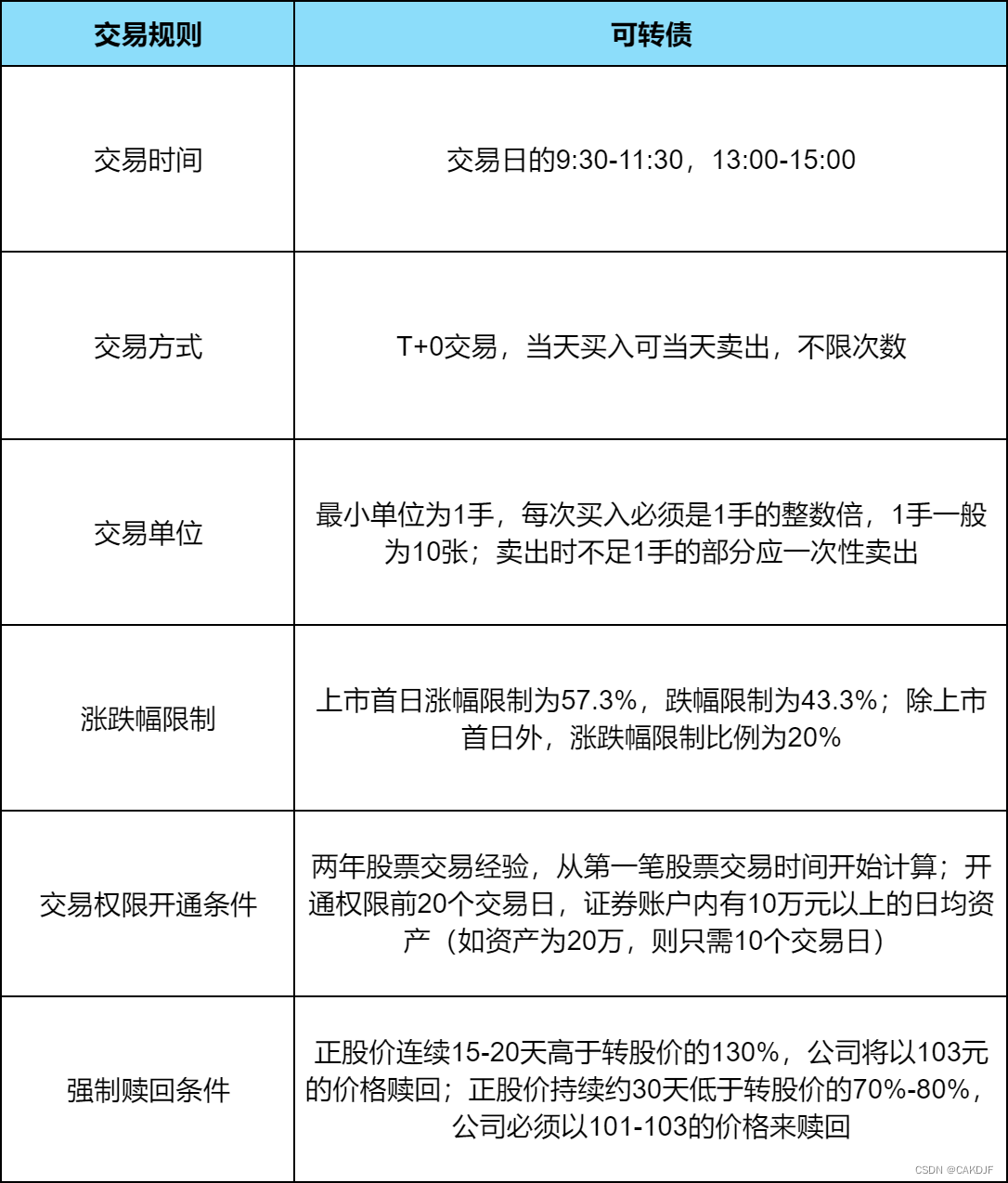
第二证券:可转债基础知识?想玩可转债一定要搞懂的交易规则!
可转债,全称是“可转化公司债券”,是上市公司为了融资,向社会公众所发行的一种债券,具有股票和债券的双重特点,投资者可以选择按照发行时约定的价格将债券转化成公司一般股票,也可作为债券持有到期后收取本…...

原型模式的实现
1. 引言 1.1 背景 在实际编程中,有时需要频繁创建多个相似但稍有不同的对象。如果采用传统的对象创建方式,容易造成代码冗余,对象重复初始化操作也可能带来大量的的资源消耗(如时间、内存等)。这样不仅降低了灵活性,导致难以适应状态的变化,还降低了代码的可扩展性。 …...

【第二套】华为 2024 年校招-硬件电源岗
1.为了避免 50Hz 的电⽹电压⼲扰放⼤器,应该⽤那种滤波器: A.带阻滤波器 B.带通滤波器 C.低通滤波器 D.⾼通滤波器 2.PID 中的 I 和 D 的作⽤分别是? A、消除静态误差和提⾼动态性能 B、消除静态误差和减⼩调节时间 C、提⾼动态性能和减⼩超调…...
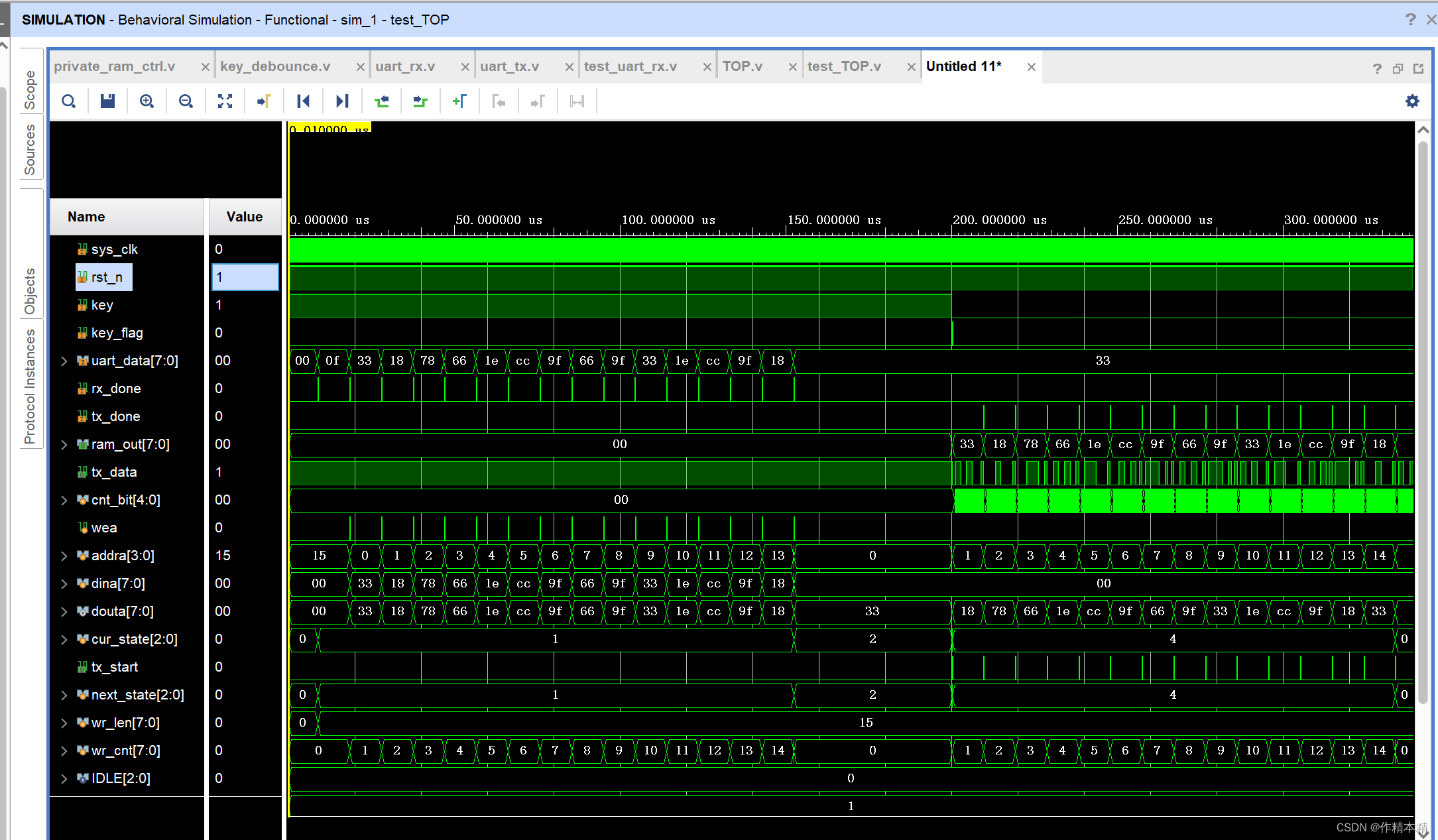
Xilinx FPGA:vivado利用单端RAM/串口传输数据实现自定义私有协议
一、项目要求 实现自定义私有协议,如:pc端产生数据:02 56 38 ,“02”代表要发送数据的个数,“56”“38”需要写进RAM中。当按键信号到来时,将“56”“38”读出返回给PC端。 二、信号流向图 三、状态…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...
