线性代数笔记
行列式
求高阶行列式
可以划上三角
上三角
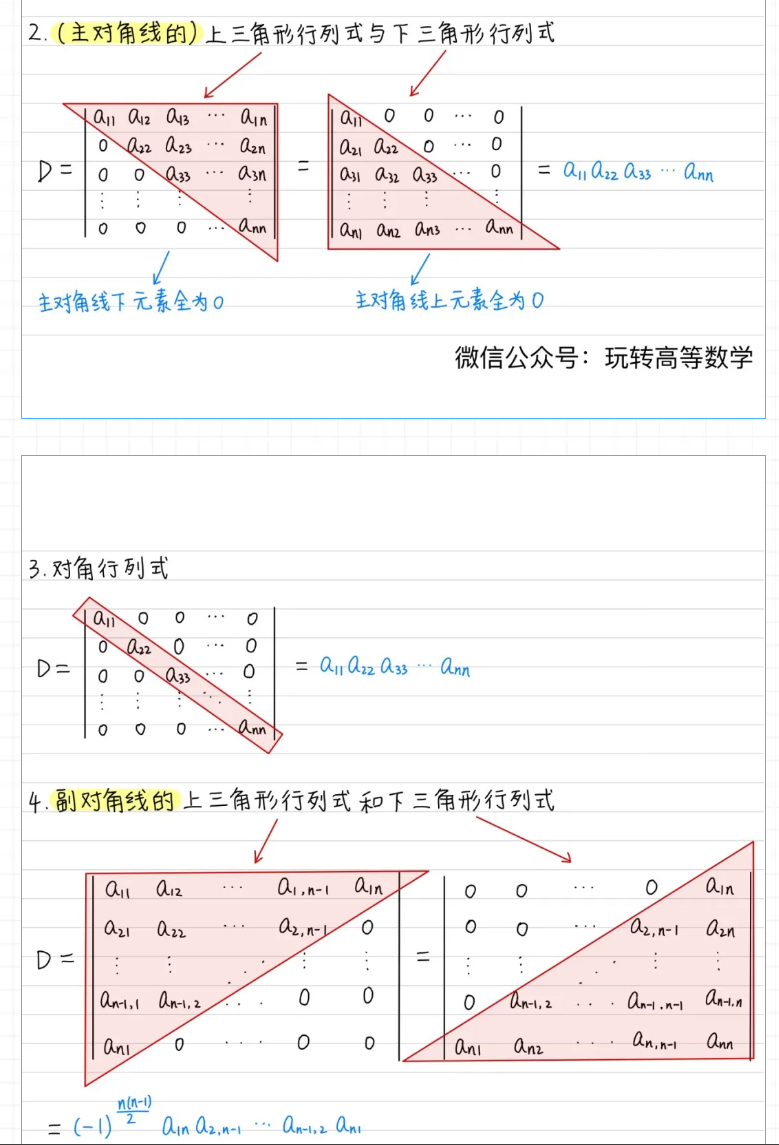
余子式
范德蒙行列式
拉普拉斯公式
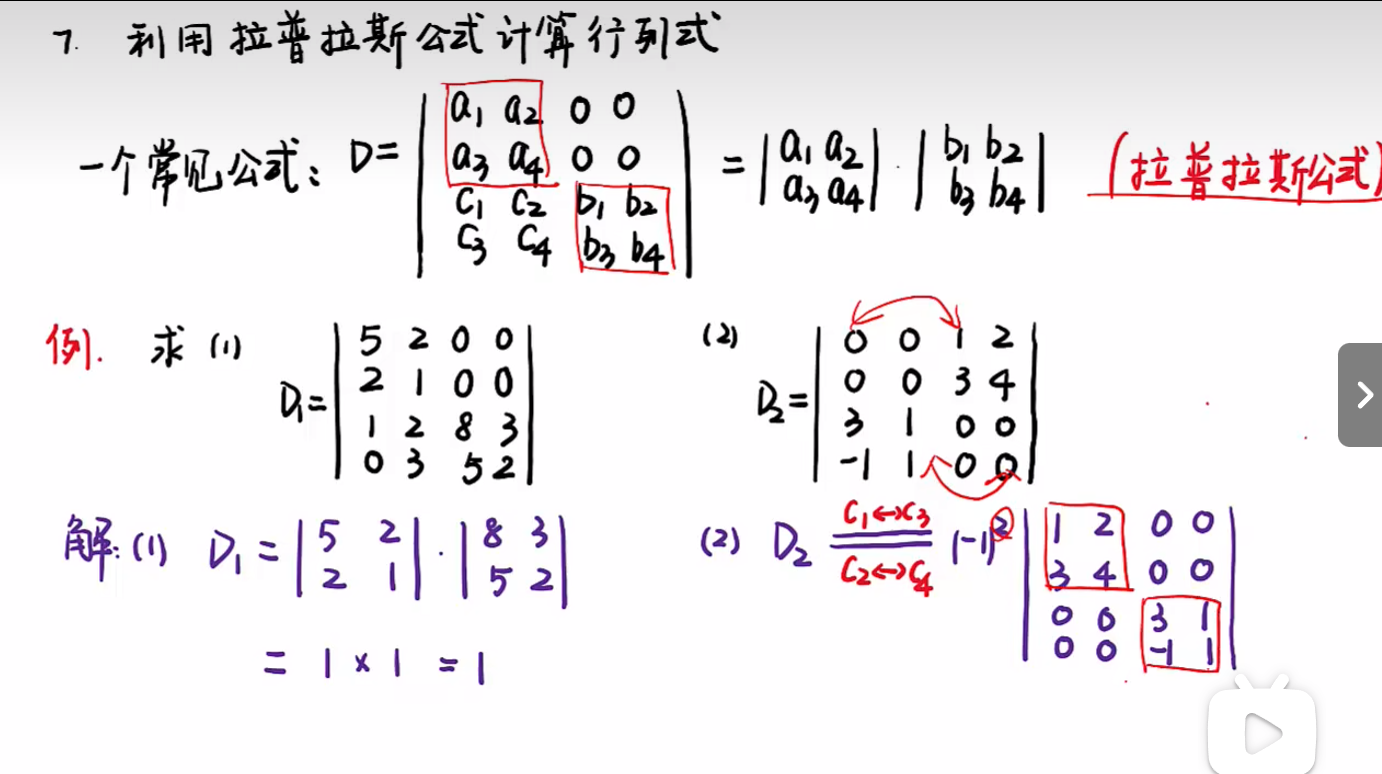
行列式行列对换值不变
矩阵
矩阵的运算
同型矩阵加减 对应位置相加减
矩阵的乘法
左边第 i 行 一次 相乘求和 右边 第 j 列
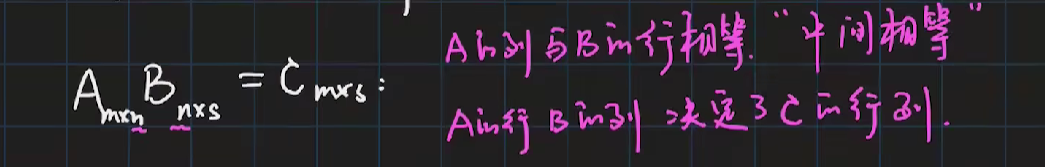
eg
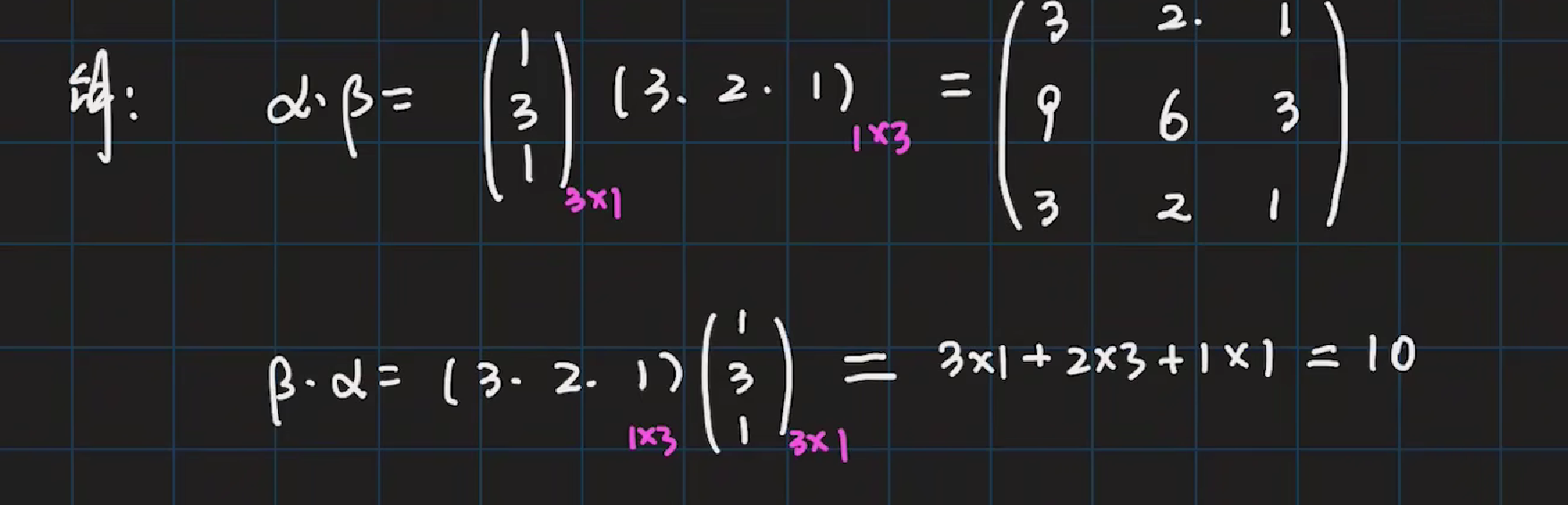
中间相等 两边规模
矩阵的幂运算
解题思路
找规律 数学归纳法
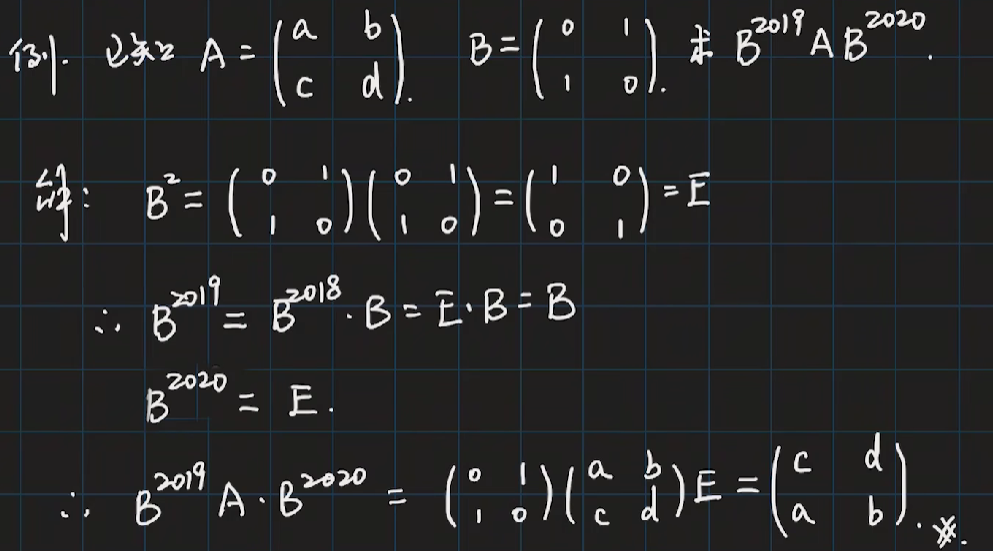
结合律
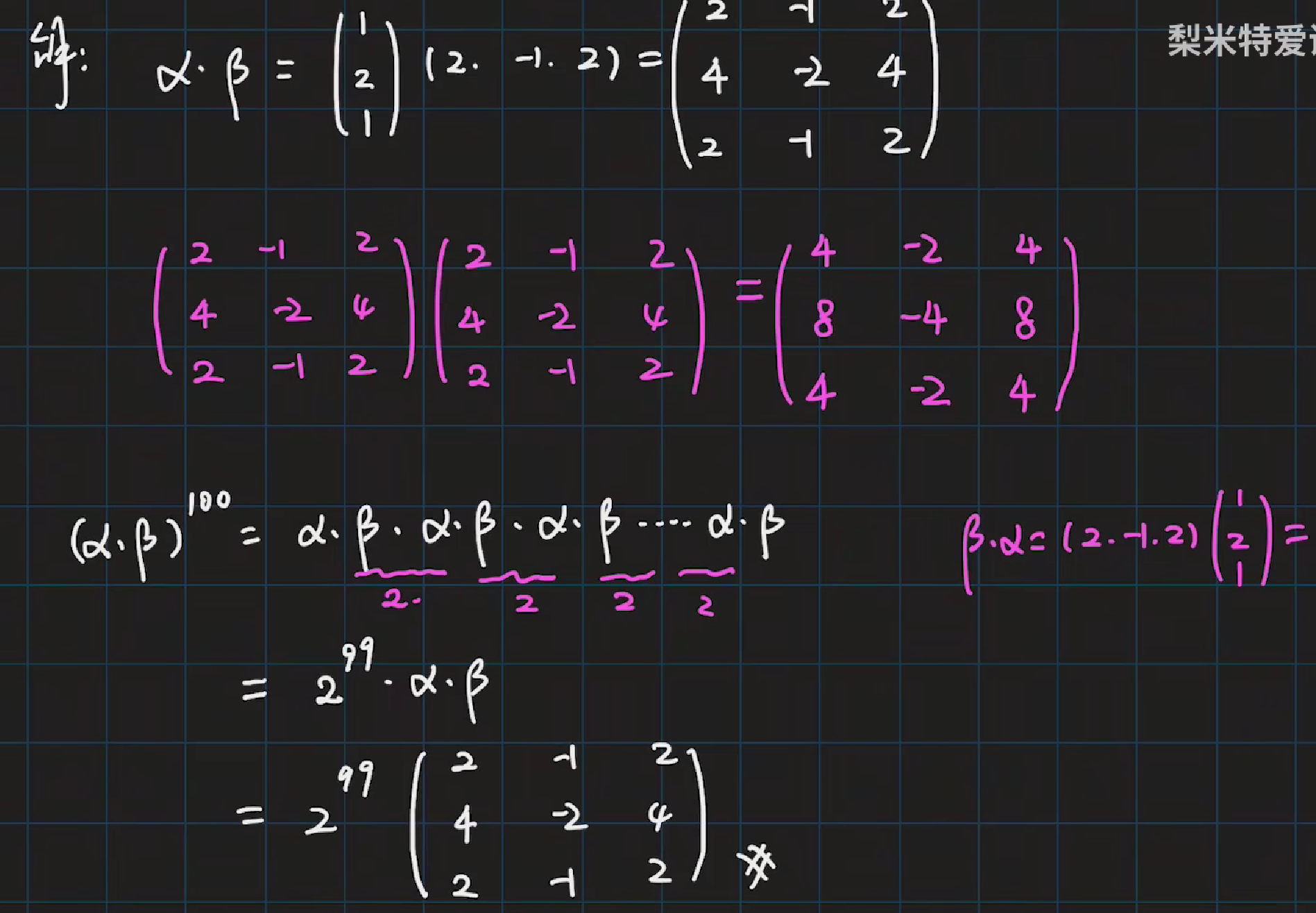
先拆 后换
矩阵的转置（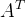
）
矩阵的行列互换
性质
方阵的行列式
行列式 行列数相等
只有方阵才有其行列式
伴随矩阵
逆 = 伴/行 伴 = 行逆
二阶方阵 其伴随矩阵 为方阵的行列式 为主对角线互换 副对角线 加负号
逆矩阵
只有方阵才可逆
- 定义 1 对于n阶方阵A，存在一个n阶方阵B，使得AB=BA=E成立，则称A是可逆矩阵，B是A的逆矩阵。记作A-1=B
单位矩阵如同乘法中的1
零矩阵不可逆
可逆矩阵的逆阵是唯一的
- 定理1 方阵A可逆的充分必要条件是|A| ≠ 0 ，且
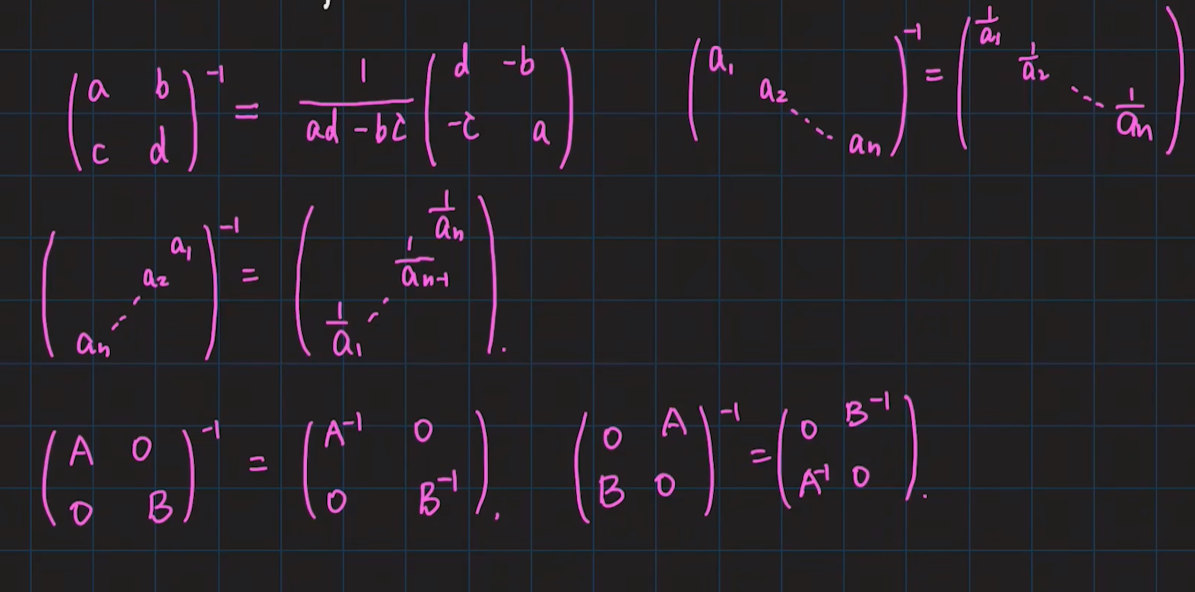
分块求 矩阵 的逆
eg
加减配凑 出结果
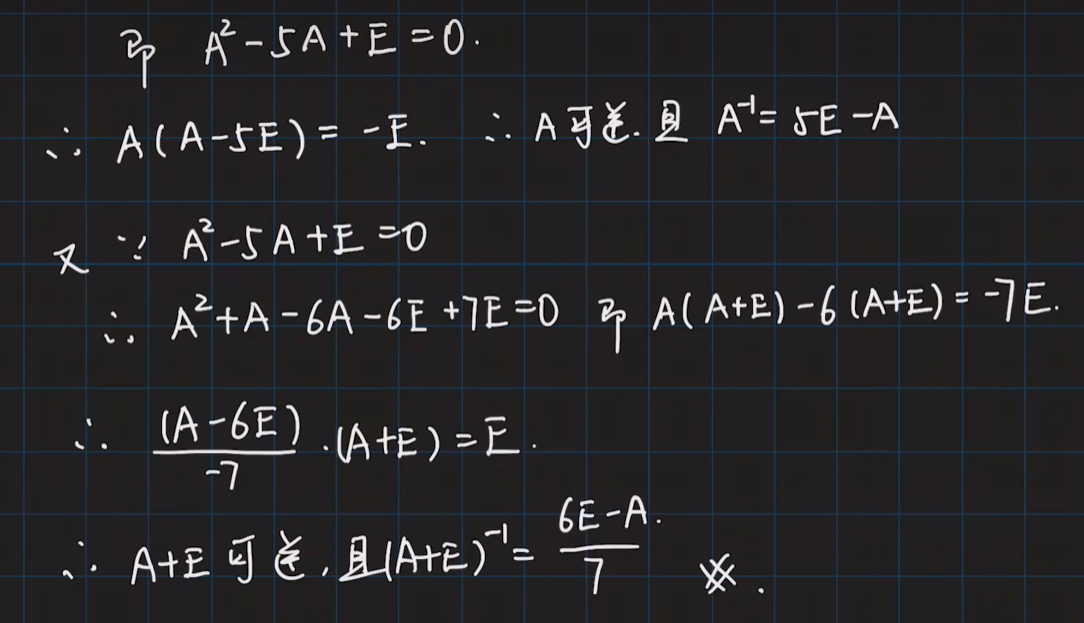
抽象矩阵求逆
数字型矩阵求逆 -- 行变换法
二阶矩阵求逆 -- 两调一除
方阵的行列式
解矩阵方程
矩阵的初等变换
行阶梯矩阵
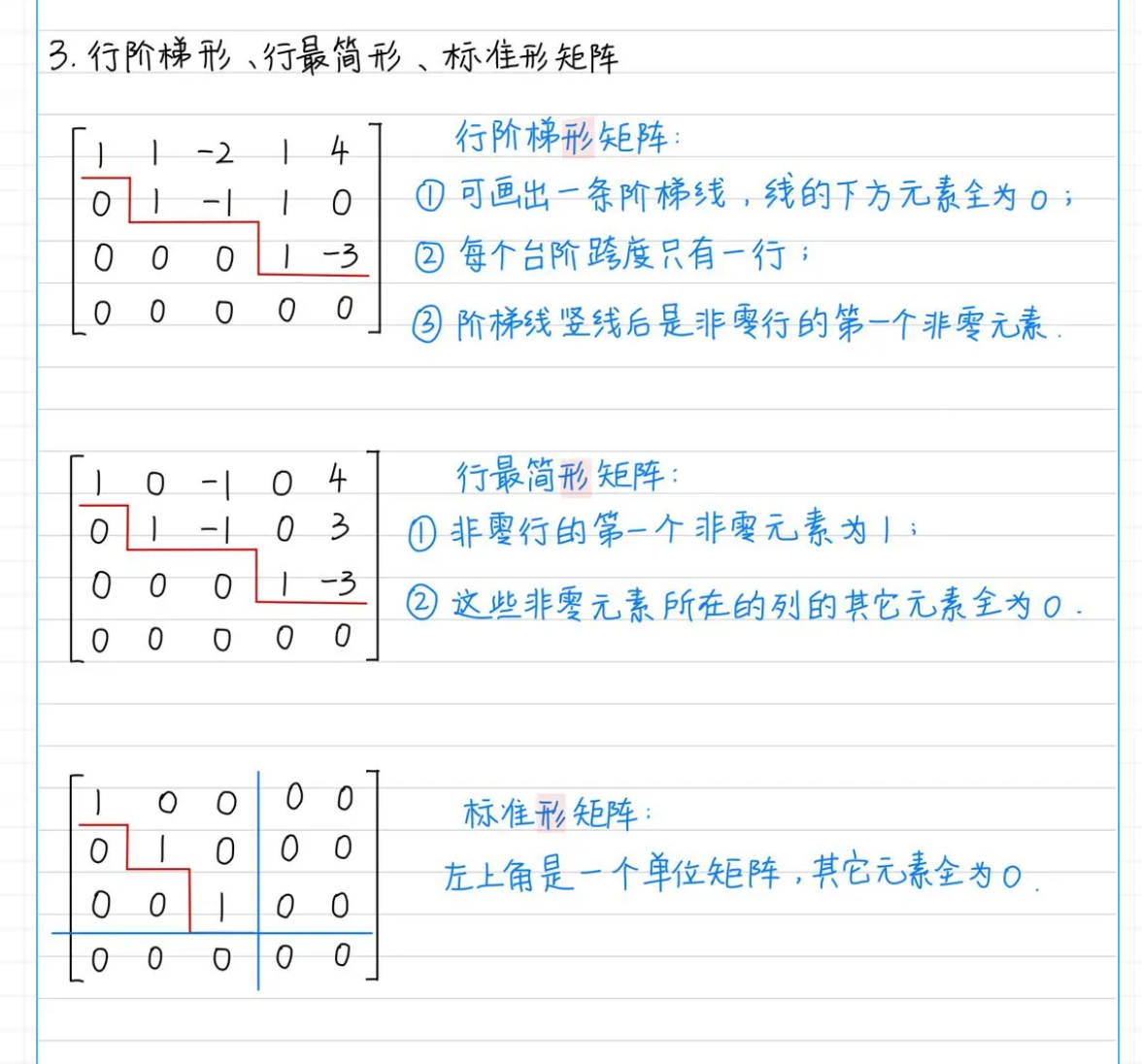
初等行列式的相关计算
eg 
矩阵的秩
性质
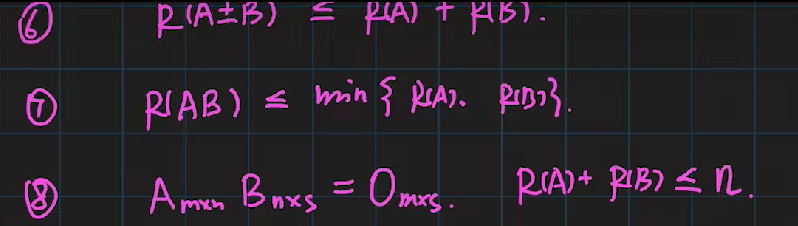
求逆矩阵
向量组的线性相关性
向量组
抽象向量组的相关性
向量组相关性计算
无关向量组增加分量个数，仍无关
线性表示相关计算
3）
与向量组的秩、最大无关组的相关计算
线性方程组求解
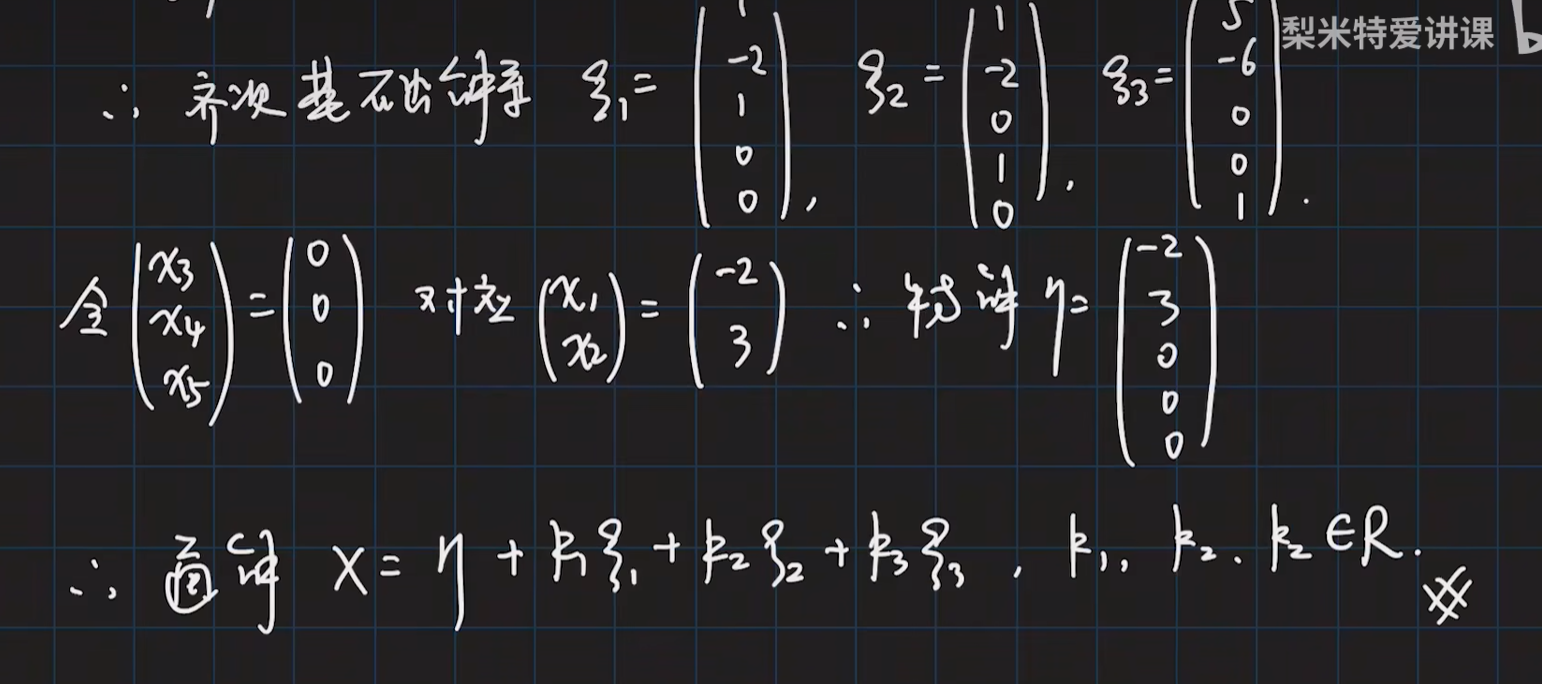
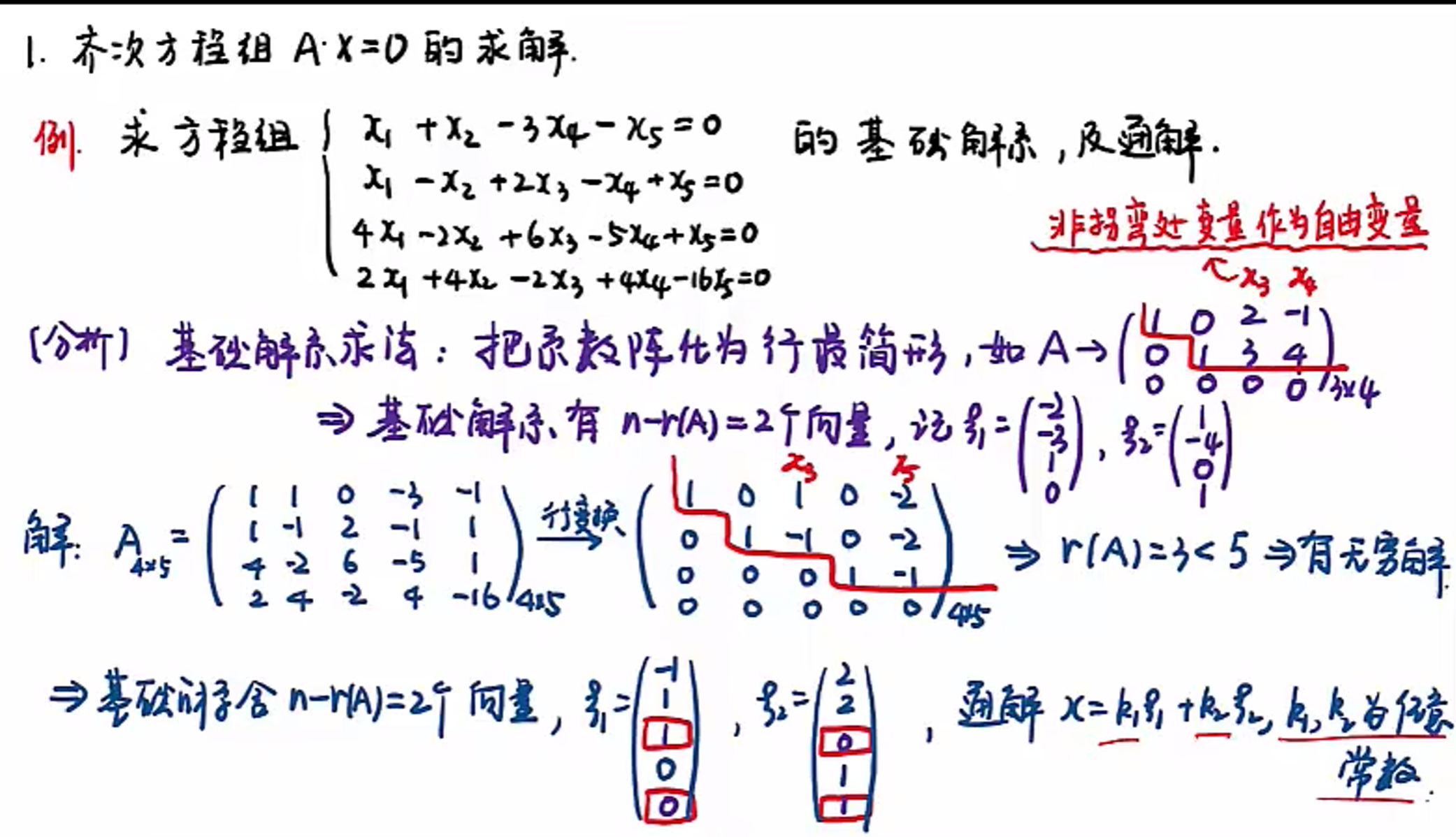
抽象性方程组的解
特征值求解
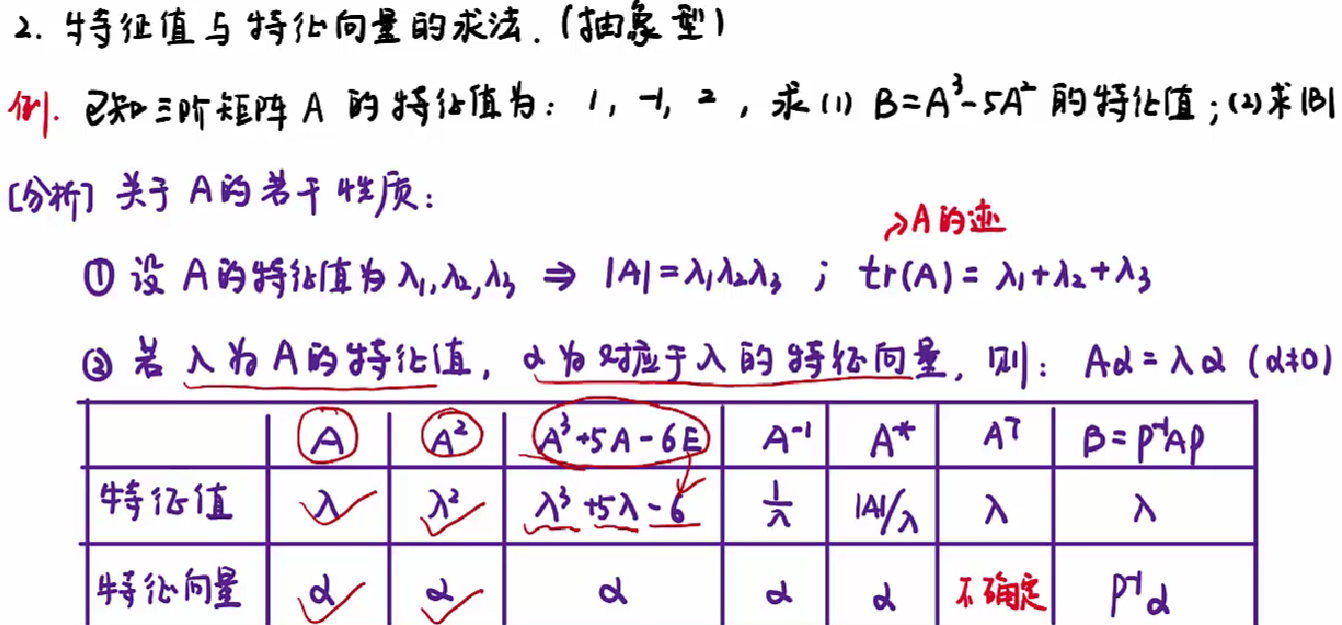
矩阵的相识对角化
对称矩阵 正交化
相关文章：
线性代数笔记
行列式 求高阶行列式 可以划上三角 上三角 余子式 范德蒙行列式 拉普拉斯公式 行列式行列对换值不变 矩阵 矩阵的运算 同型矩阵加减 对应位置相加减 矩阵的乘法 左边第 i 行 一次 相乘求和 右边 第 j 列 eg 中间相等 两边规模 矩阵的幂运算 解题思路 找规律 数学归纳…...
未公开 GeoServer开源服务器wfs远程命令执行漏洞 已复现(CVE-2024-36401)
0x01 阅读须知 技术文章仅供参考，此文所提供的信息只为网络安全人员对自己所负责的网站、服务器等（包括但不限于）进行检测或维护参考，未经授权请勿利用文章中的技术资料对任何计算机系统进行入侵操作。利用此文所提供的信息而造成…...
【WebGIS干货分享】Webgis 面试题-浙江中海达
1、Cesium 中有几种拾取坐标的方式，分别介绍 Cesium 是一个用于创建 3D 地球和地理空间应用的 JavaScript 库。在 Cesium 中，你可以使用不同的方式来拾取坐标，以便与地球或地图上的对象进行交 互。以下是 Cesium 中几种常见的拾取坐标的方式…...
ES 修改索引字段类型
大体的原理： 1：按照老索引按需修改，新建新索引 2：转移数据（数据量大，时间会很长） 3：删除老索引 4：给新索引 创建别名 第一步：创建新索引 可以先获取老索引ma…...
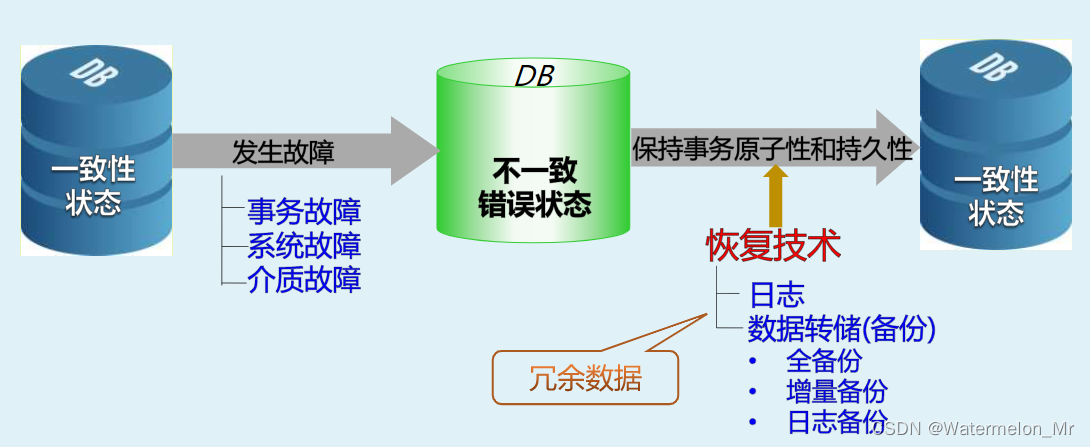
恢复的实现技术-日志和数据转储
一、引言 在系统正常运行的情况下，事务处理的恢复机制应采取某些技术措施为恢复做好相应的准备，保证在系统发生故障后，能将数据库从一个不一致的错误状态恢复到一个一致性状态 恢复技术主要包括 生成一个数据库日志，来记录系统中…...
全网最全最细的jmeter接口测试教程，建议收藏
在日常工作中，尤其是做接口测试时，我们最经常用到的两个工具，就是Jmeter和postman。今天，我们主要是讲一讲Jmeter在接口测试这一块的一些方式方法。内容比较多，大家可以收藏一下，以后慢慢学。 1࿰…...
Raspbian命令行连接WiFi网络
Raspbian命令行连接WiFi网络 1. 源由2. 环境3. 信号4. 连接5. 检查6. 断开 1. 源由 “懒人”多福，是什么原因，大家知道不，哈哈。 如果大家关注过之前《Ardupilot开源代码之Rover上路计划》，为了笔记本电脑在不断网的情况下进行配…...
王佩丰 Excel 基础二十四讲——目录
前言 跟着B站学习王佩丰 Excel 基础教程，本文章为索引目录 课程传送门：视频地址——点击前往 王佩丰Excel基础教程24讲完整版 第一讲：认识 Excel 第二讲：Excel 单元格格式设置 第三讲：查找替换定位（未编辑…...
Qt扫盲-QRect矩形描述类
QRect矩形描述总结 一、概述二、常用函数1. 移动类2. 属性函数3. 判断4. 比较计算 三、渲染三、坐标 一、概述 QRect类使用整数精度在平面中定义一个矩形。在绘图的时候经常使用，作为一个二维的参数描述类。 一个矩形主要有两个重要属性，一个是坐标&am…...
Android系统adb shell怎么执行checksum 来判断文件是否变更？
在Android系统中，通过ADB（Android Debug Bridge）shell执行checksum（校验和）来检查文件是否变更是一个常见的需求，尤其是在自动化测试或确保应用文件未被篡改的场景中。在Linux和Android shell中，…...
JS中的上下文
一.执行上下文的概念： 执行上下文简称上下文。变量或者函数的上下文决定了它们可以访问哪些数据，以及它们的行为。每一个上下文都具有一个关联的变量对象，而这个上下文中定义的所有变量和函数都存在于这个对象上。 二.JS中上下文的执行机制&a…...
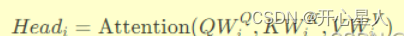
【深度学习】注意力机制
https://blog.csdn.net/weixin_43334693/article/details/130189238 https://blog.csdn.net/weixin_47936614/article/details/130466448 https://blog.csdn.net/qq_51320133/article/details/138305880 注意力机制：在处理信息的时候，会将注意力放在需要…...
安卓开发自定义时间日期显示组件
安卓开发自定义时间日期显示组件 问题背景 实现时间和日期显示，左对齐和对齐两种效果，如下图所示： 问题分析 自定义view实现一般思路： （1）自定义一个View （2）编写values/attrs.…...
IT行业入门，如何假期逆袭，实现抢跑
目录 前言 1.IT行业领域分类 2.基础课程预习指南 3.技术学习路线 4.学习资源推荐 结束语 前言 IT（信息技术）行业是一个非常广泛和多样化的领域，它包括了许多不同的专业领域和职业路径。如果要进军IT行业，我们应该要明确自己…...
Pyramid 中混合认证策略
1. 问题背景 在一个使用 Pyramid 框架开发的应用程序中，需要同时处理 HTML 内容的显示和 JSON API 的请求。对于 HTML 内容，使用了 AuthTktAuthenticationPolicy 进行身份验证和 ACLAuthorizationPolicy 进行授权。当用户成功登录后，会在浏览…...
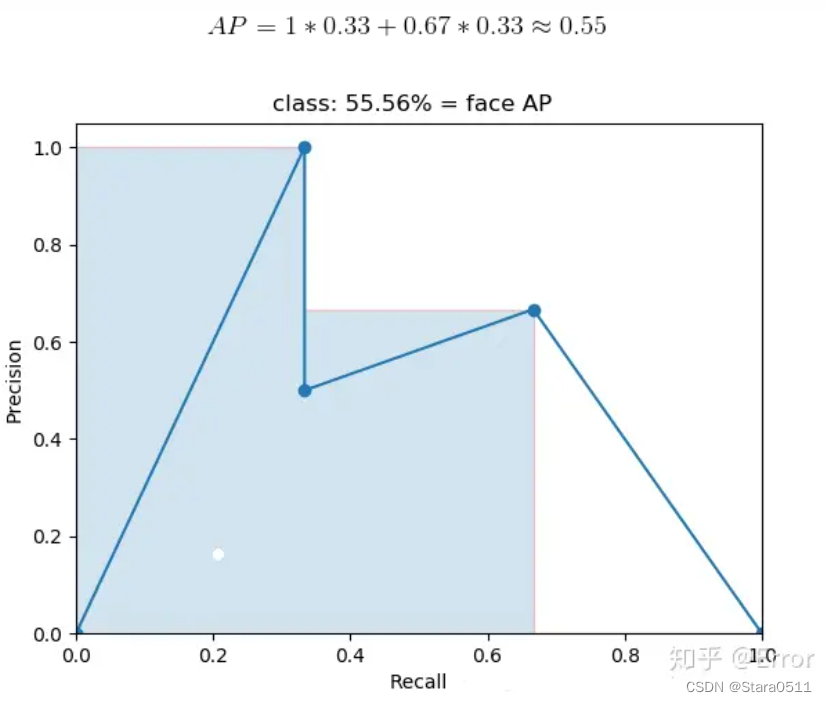
深度学习经典检测方法概述
一、深度学习经典检测方法 two-stage（两阶段）：Faster-rcnn Mask-Rcnn系列 one-stage（单阶段）：YOLO系列 1. one-stage 最核心的优势：速度非常快，适合做实时检测任务！ 但是…...
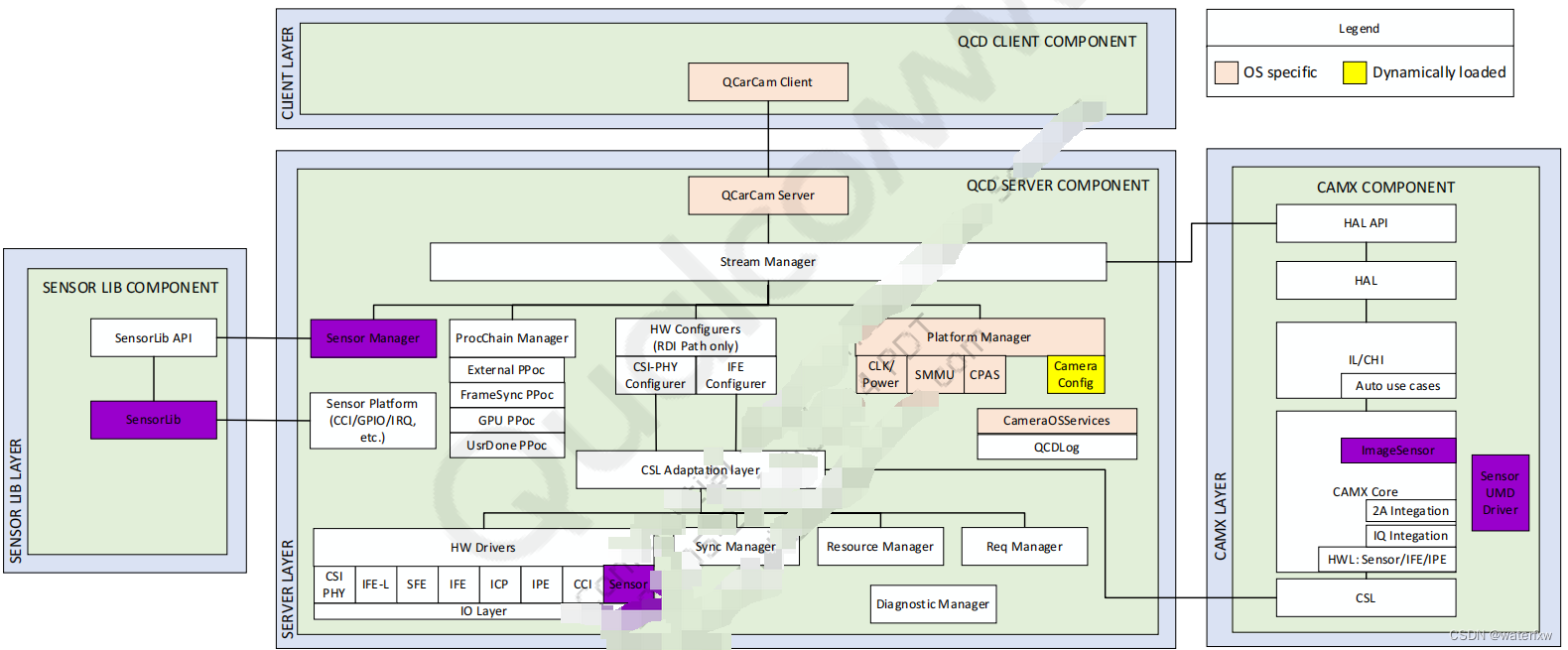
＜sa8650＞sa8650 qcxserver-之-摄像头传感器VB56G4A驱动开发＜1＞
＜sa8650＞sa8650 qcxserver-之-摄像头传感器VB56G4A驱动开发 <1> 一、前言二、QCX架构三、QCX 传感器驱动程序定制开发3.1 sensor硬件接口3.2 sensor配置文件3.2.1 cameraconfig.c3.2.2 cameraconfigsa8650_water.c3.2.3 新增编译MK3.2.4 参数解析3.2.4.1 struct Camera…...
推荐8款超实用的ComfyUI绘画插件，帮助我们的AI绘画质量和效率提升几个档次！
前言 大家在使用SD绘画过程中，想必见识到了插件的强大功能，本身纯净版的SD界面是相对简洁的，但是搭配了各种插件后，界面标签栏会增加很多，相应的功能也增加了。 从简单的中文界面翻译插件，到强大的contro…...
MATLAB-振动问题：两自由度耦合系统自由振动
一、基本理论 二、MATLAB实现 以下是两自由度耦合系统自由振动质量块振动过程动画显示的MATLAB程序。 clear; clc; close allx0 1; D1 40; D12 8; D2 D1; m1 1; omega0 sqrt(D1/m1); k1 D12 / D1; k2 D12 / D2; k sqrt(k1 * k2); omegazh omega0 * sqrt(1 k); omeg…...
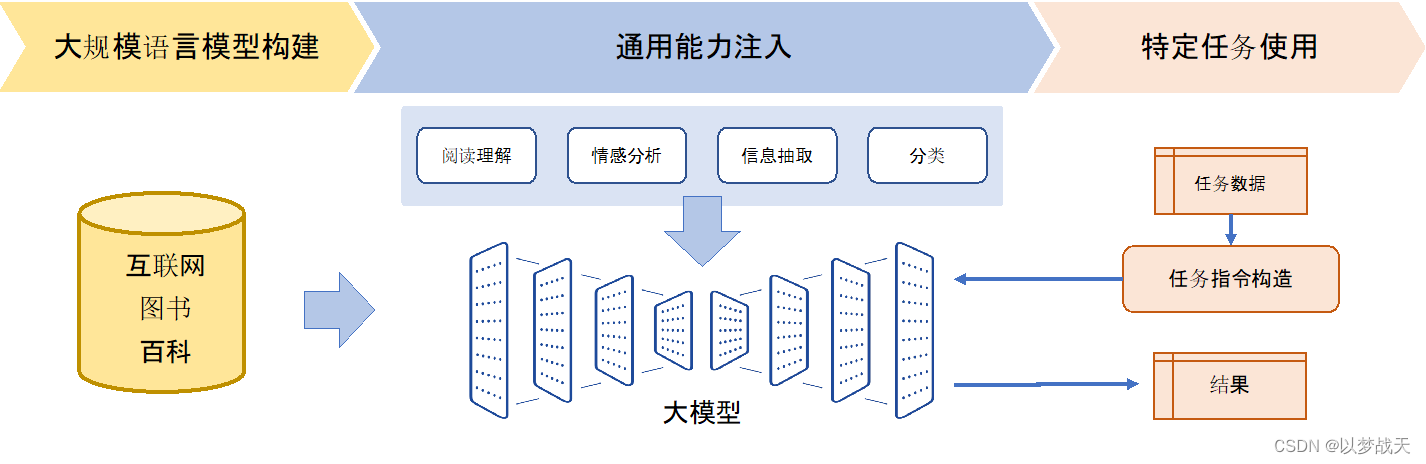
人工智能-NLP简单知识汇总01
人工智能-NLP简单知识汇总01 1.1自然语言处理的基本概念 自然语言处理难点： 语音歧义句子切分歧义词义歧义结构歧义代指歧义省略歧义语用歧义 总而言之：！！语言无处不歧义 1.2自然语言处理的基本范式 1.2.1基于规则的方法 通…...
零门槛NAS搭建：WinNAS如何让普通电脑秒变私有云？
一、核心优势：专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发，是一款收费低廉但功能全面的Windows NAS工具，主打“无学习成本部署” 。与其他NAS软件相比，其优势在于： 无需硬件改造：将任意W…...
label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...
Cesium1.95中高性能加载1500个点
一、基本方式： 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...
数据链路层的主要功能是什么
数据链路层（OSI模型第2层）的核心功能是在相邻网络节点（如交换机、主机）间提供可靠的数据帧传输服务，主要职责包括： 🔑 核心功能详解： 帧封装与解封装 封装： 将网络层下发…...
华为云Flexus+DeepSeek征文｜DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文｜DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色，华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型，能助力我们轻松驾驭 DeepSeek-V3/R1，本文中将分享如何…...
【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控，故障处理工具
第2章 虚拟机性能监控，故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令：jps [options] [hostid] 功能：本地虚拟机进程显示进程ID（与ps相同），可同时显示主类&#x…...
关键领域软件测试的突围之路：如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天，软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件，这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下，实现高效测试与快速迭代？这一命题正考验着…...
算法笔记2
1.字符串拼接最好用StringBuilder，不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...
SiFli 52把Imagie图片，Font字体资源放在指定位置，编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍： img 属性指定分区存放的 image 名称，指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件，则以 proj_name:binary_name 格式指定文件名， proj_name 为工程 名&…...
《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板，就像一个模具，里面可以将不同类型的材料做成一个形状，其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式：templa…...