【状态估计】线性高斯系统的状态估计——离散时间的递归滤波
前两篇文章介绍了离散时间的批量估计、离散时间的递归平滑,本文着重介绍离散时间的递归滤波。
前两篇位置:【状态估计】线性高斯系统的状态估计——离散时间的批量估计、【状态估计】线性高斯系统的状态估计——离散时间的递归平滑。
离散时间的递归滤波算法
批量优化的方案及其对应的平滑算法方案,是LG问题下能找到的最好的方法了。它利用了所有能用的数据,来估计所有时刻的状态。不过这个方法有一个致命的问题:无法在线运行,因为它需要用未来时刻的信息估计过去的状态。为了在实时场合下使用,当前时刻的状态只能由它之前时间的信息决定,而卡尔曼滤波则是对这样一个问题的传统解决方案。
之前讲述了如何从Cholesky分解推导出卡尔曼滤波,实际上并不需要这么复杂,接下来介绍几种推导卡尔曼滤波的方法。
通过MAP推导卡尔曼滤波
假设已经有了 k − 1 k-1 k−1时刻的前向估计:
{ x ^ k − 1 , P ^ k − 1 } \{\hat x_{k-1},\hat P_{k-1}\} {x^k−1,P^k−1}
这两个量是根据初始时刻到 k − 1 k-1 k−1时刻的数据推导出来的。目标是计算:
{ x ^ k , P ^ k } \{\hat x_k,\hat P_k\} {x^k,P^k}
其中,需要用到直到 k k k时刻的数据。实际上没有必要再从初始时刻开始,而是简单地用 k − 1 k-1 k−1时刻的状态,以及 k k k时刻的 v k v_k vk、 y k y_k yk就能估计出 k k k时刻的状态了:
{ x ^ k − 1 , P ^ k − 1 , v k , y k } − − > { x ^ k , P ^ k } \{\hat x_{k-1},\hat P_{k-1},v_k,y_k\}-->\{\hat x_k,\hat P_k\} {x^k−1,P^k−1,vk,yk}−−>{x^k,P^k}
为了推导这个过程,定义:
z = [ x ^ k − 1 v k y k ] z=\begin{bmatrix}\hat x_{k-1}\\v_k\\y_k\end{bmatrix} z= x^k−1vkyk
H = [ 1 − A k − 1 1 C k ] H=\begin{bmatrix}1\\-A_{k-1}&1\\&C_k\end{bmatrix} H= 1−Ak−11Ck
W = [ P ^ k − 1 Q k R k ] W=\begin{bmatrix}\hat P_{k-1}\\&Q_k\\&&R_k\end{bmatrix} W= P^k−1QkRk
x ^ = [ x ^ k − 1 ′ x ^ k ] \hat x=\begin{bmatrix}\hat x_{k-1}^{'}\\\hat x_k\end{bmatrix} x^=[x^k−1′x^k]
其中, x ^ k − 1 ′ \hat x_{k-1}^{'} x^k−1′表示使用了直到 k k k时刻的数据计算的 k − 1 k-1 k−1时刻的状态估计,而 x ^ k − 1 \hat x_{k-1} x^k−1表示使用了直到 k − 1 k-1 k−1时刻的数据计算的 k − 1 k-1 k−1时刻的状态估计,两者之间相差一个 k k k时刻的后向估计。
通常MAP的最优解 x ^ \hat x x^写成:
( H T W − 1 H ) x ^ = H T W − 1 z (H^TW^{-1}H)\hat x=H^TW^{-1}z (HTW−1H)x^=HTW−1z
将上面的定义代入:
[ P ^ k − 1 − 1 + A k − 1 T Q k − 1 A k − 1 − A k − 1 T Q k − 1 − Q k − 1 A k − 1 Q k − 1 + C k T R k − 1 C k ] [ x ^ k − 1 ′ x ^ k ] = [ P ^ k − 1 − 1 x ^ k − 1 − A k − 1 T Q k − 1 v k Q k − 1 v k + C k T R k − 1 y k ] \begin{bmatrix}\hat P_{k-1}^{-1}+A_{k-1}^TQ_k^{-1}A_{k-1}&-A_{k-1}^TQ_k^{-1}\\-Q_k^{-1}A_{k-1}&Q_k^{-1}+C_k^TR_k^{-1}C_k\end{bmatrix}\begin{bmatrix}\hat x_{k-1}^{'}\\\hat x_k\end{bmatrix}=\begin{bmatrix}\hat P_{k-1}^{-1}\hat x_{k-1}-A_{k-1}^TQ_k^{-1}v_k\\Q_k^{-1}v_k+C^T_kR_k^{-1}y_k\end{bmatrix} [P^k−1−1+Ak−1TQk−1Ak−1−Qk−1Ak−1−Ak−1TQk−1Qk−1+CkTRk−1Ck][x^k−1′x^k]=[P^k−1−1x^k−1−Ak−1TQk−1vkQk−1vk+CkTRk−1yk]
由于并不关心 x ^ k − 1 ′ \hat x_{k-1}^{'} x^k−1′的实际值,因此可以将它边缘化,等式两侧左乘:
[ 1 0 Q k − 1 A k − 1 ( P ^ k − 1 − 1 + A k − 1 T Q k − 1 A k − 1 ) − 1 1 ] \begin{bmatrix}1&0\\Q_k^{-1}A_{k-1}(\hat P_{k-1}^{-1}+A_{k-1}^TQ_k^{-1}A_{k-1})^{-1}&1\end{bmatrix} [1Qk−1Ak−1(P^k−1−1+Ak−1TQk−1Ak−1)−101]
这是一元线性方程的行操作,于是变成:
[ P ^ k − 1 − 1 + A k − 1 T Q k − 1 A k − 1 − A k − 1 T Q k − 1 0 Q k − 1 − Q k − 1 A k − 1 ( P ^ k − 1 − 1 + A k − 1 T Q k − 1 A k − 1 ) − 1 A k − 1 T Q k − 1 + C k T R k − 1 C k ] [ x ^ k − 1 ′ x ^ k ] = [ P ^ k − 1 − 1 x ^ k − 1 − A k − 1 T Q k − 1 v k Q k − 1 A k − 1 ( P ^ k − 1 − 1 + A k − 1 T Q k − 1 A k − 1 ) − 1 ( P ^ k − 1 − 1 x ^ k − 1 − A k − 1 T Q k − 1 v k ) + Q k − 1 v k + C k T R k − 1 y k ] \begin{bmatrix}\hat P_{k-1}^{-1}+A_{k-1}^TQ_k^{-1}A_{k-1}&-A_{k-1}^TQ_k^{-1}\\0&Q_k^{-1}-Q_k^{-1}A_{k-1}(\hat P_{k-1}^{-1}+A_{k-1}^TQ_k^{-1}A_{k-1})^{-1}A_{k-1}^TQ_k^{-1}+C_k^TR_k^{-1}C_k\end{bmatrix}\begin{bmatrix}\hat x_{k-1}^{'}\\\hat x_k\end{bmatrix}=\begin{bmatrix}\hat P_{k-1}^{-1}\hat x_{k-1}-A_{k-1}^TQ_k^{-1}v_k\\Q_k^{-1}A_{k-1}(\hat P_{k-1}^{-1}+A_{k-1}^TQ_k^{-1}A_{k-1})^{-1}(\hat P_{k-1}^{-1}\hat x_{k-1}-A_{k-1}^TQ_k^{-1}v_k)+Q_k^{-1}v_k+C_k^TR_k^{-1}y_k\end{bmatrix} [P^k−1−1+Ak−1TQk−1Ak−10−Ak−1TQk−1Qk−1−Qk−1Ak−1(P^k−1−1+Ak−1TQk−1Ak−1)−1Ak−1TQk−1+CkTRk−1Ck][x^k−1′x^k]=[P^k−1−1x^k−1−Ak−1TQk−1vkQk−1Ak−1(P^k−1−1+Ak−1TQk−1Ak−1)−1(P^k−1−1x^k−1−Ak−1TQk−1vk)+Qk−1vk+CkTRk−1yk]
因此,只需要关注 x ^ k \hat x_k x^k:
( Q k − 1 − Q k − 1 A k − 1 ( P ^ k − 1 − 1 + A k − 1 T Q k − 1 A k − 1 ) − 1 A k − 1 T Q k − 1 + C k T R k − 1 C k ) x ^ k = Q k − 1 A k − 1 ( P ^ k − 1 − 1 + A k − 1 T Q k − 1 A k − 1 ) − 1 ( P ^ k − 1 − 1 x ^ k − 1 − A k − 1 T Q k − 1 v k ) + Q k − 1 v k + C k T R k − 1 y k (Q_k^{-1}-Q_k^{-1}A_{k-1}(\hat P_{k-1}^{-1}+A_{k-1}^TQ_k^{-1}A_{k-1})^{-1}A_{k-1}^TQ_k^{-1}+C_k^TR_k^{-1}C_k)\hat x_k=Q_k^{-1}A_{k-1}(\hat P_{k-1}^{-1}+A_{k-1}^TQ_k^{-1}A_{k-1})^{-1}(\hat P_{k-1}^{-1}\hat x_{k-1}-A_{k-1}^TQ_k^{-1}v_k)+Q_k^{-1}v_k+C_k^TR_k^{-1}y_k (Qk−1−Qk−1Ak−1(P^k−1−1+Ak−1TQk−1Ak−1)−1Ak−1TQk−1+CkTRk−1Ck)x^k=Qk−1Ak−1(P^k−1−1+Ak−1TQk−1Ak−1)−1(P^k−1−1x^k−1−Ak−1TQk−1vk)+Qk−1vk+CkTRk−1yk
根据SMW恒等式:
Q k − 1 − Q k − 1 A k − 1 ( P ^ k − 1 − 1 + A k − 1 T Q k − 1 A k − 1 ) − 1 A k − 1 T Q k − 1 = ( Q k + A k − 1 P ^ k − 1 A k − 1 T ) − 1 Q_k^{-1}-Q_k^{-1}A_{k-1}(\hat P_{k-1}^{-1}+A_{k-1}^TQ_k^{-1}A_{k-1})^{-1}A_{k-1}^TQ_k^{-1}=(Q_k+A_{k-1}\hat P_{k-1}A_{k-1}^T)^{-1} Qk−1−Qk−1Ak−1(P^k−1−1+Ak−1TQk−1Ak−1)−1Ak−1TQk−1=(Qk+Ak−1P^k−1Ak−1T)−1
定义:
P ˇ k = Q k + A k − 1 P ^ k − 1 A k − 1 T \check P_k=Q_k+A_{k-1}\hat P_{k-1}A_{k-1}^T Pˇk=Qk+Ak−1P^k−1Ak−1T
P ^ k = ( P ˇ k − 1 + C k T R k − 1 C k ) − 1 \hat P_k=(\check P_k^{-1}+C_k^TR_k^{-1}C_k)^{-1} P^k=(Pˇk−1+CkTRk−1Ck)−1
原式可化简为:
P ^ k − 1 x ^ k = Q k − 1 A k − 1 ( P ^ k − 1 − 1 + A k − 1 T Q k − 1 A k − 1 ) − 1 ( P ^ k − 1 − 1 x ^ k − 1 − A k − 1 T Q k − 1 v k ) + Q k − 1 v k + C k T R k − 1 y k = Q k − 1 A k − 1 ( P ^ k − 1 − 1 + A k − 1 T Q k − 1 A k − 1 ) − 1 P ^ k − 1 − 1 x ^ k − 1 + ( Q k − 1 − Q k − 1 A k − 1 ( P ^ k − 1 − 1 + A k − 1 T Q k − 1 A k − 1 ) − 1 A k − 1 T Q k − 1 ) v k + C k T R k − 1 y k = P ˇ k − 1 A k − 1 x ^ k − 1 + P ˇ k − 1 v k + C k T R k − 1 y k = P ˇ k − 1 ( A k − 1 x ^ k − 1 + v k ) + C k T R k − 1 y k = P ˇ k − 1 x ˇ k + C k T R k − 1 y k \begin{aligned}\hat P_k^{-1}\hat x_k&=Q_k^{-1}A_{k-1}(\hat P_{k-1}^{-1}+A_{k-1}^TQ_k^{-1}A_{k-1})^{-1}(\hat P_{k-1}^{-1}\hat x_{k-1}-A_{k-1}^TQ_k^{-1}v_k)+Q_k^{-1}v_k+C_k^TR_k^{-1}y_k \\&=Q_k^{-1}A_{k-1}(\hat P_{k-1}^{-1}+A_{k-1}^TQ_k^{-1}A_{k-1})^{-1}\hat P_{k-1}^{-1}\hat x_{k-1}+(Q_k^{-1}-Q_k^{-1}A_{k-1}(\hat P_{k-1}^{-1}+A_{k-1}^TQ_k^{-1}A_{k-1})^{-1}A_{k-1}^TQ_k^{-1})v_k+C_k^TR_k^{-1}y_k \\&=\check P_k^{-1}A_{k-1}\hat x_{k-1}+\check P_k^{-1}v_k+C_k^TR_k^{-1}y_k \\ &=\check P_k^{-1}(A_{k-1}\hat x_{k-1}+v_k)+C_k^TR_k^{-1}y_k \\ &=\check P_k^{-1}\check x_k+C_k^TR_k^{-1}y_k\end{aligned} P^k−1x^k=Qk−1Ak−1(P^k−1−1+Ak−1TQk−1Ak−1)−1(P^k−1−1x^k−1−Ak−1TQk−1vk)+Qk−1vk+CkTRk−1yk=Qk−1Ak−1(P^k−1−1+Ak−1TQk−1Ak−1)−1P^k−1−1x^k−1+(Qk−1−Qk−1Ak−1(P^k−1−1+Ak−1TQk−1Ak−1)−1Ak−1TQk−1)vk+CkTRk−1yk=Pˇk−1Ak−1x^k−1+Pˇk−1vk+CkTRk−1yk=Pˇk−1(Ak−1x^k−1+vk)+CkTRk−1yk=Pˇk−1xˇk+CkTRk−1yk
梳理一下整个过程:
预测:
x ˇ k = A k − 1 x ^ k − 1 + v k P ˇ k = A k − 1 P ^ k − 1 A k − 1 T + Q k \begin{aligned}\check x_k&=A_{k-1}\hat x_{k-1}+v_k \\ \check P_k&=A_{k-1}\hat P_{k-1}A_{k-1}^T+Q_k\end{aligned} xˇkPˇk=Ak−1x^k−1+vk=Ak−1P^k−1Ak−1T+Qk
更新:
P ^ k = ( P ˇ k − 1 + C k T R k − 1 C k ) − 1 P ^ k − 1 x ^ k = P ˇ k − 1 x ˇ k + C k T R k − 1 y k \begin{aligned}\hat P_k&=(\check P_k^{-1}+C_k^TR_k^{-1}C_k)^{-1} \\ \hat P_k^{-1}\hat x_k&=\check P_k^{-1}\check x_k+C_k^TR_k^{-1}y_k\end{aligned} P^kP^k−1x^k=(Pˇk−1+CkTRk−1Ck)−1=Pˇk−1xˇk+CkTRk−1yk
这是逆协方差形式(信息形式)的卡尔曼滤波。为了得到经典形式的卡尔曼滤波,需要定义卡尔曼增益 K k K_k Kk:
K k = P ^ k C k T R k − 1 K_k=\hat P_kC_k^TR_k^{-1} Kk=P^kCkTRk−1
经过化简,更新:
K k = P ˇ k C k T ( C k P ˇ k C k T + R k ) − 1 P ^ k = ( 1 − K k C k ) P ˇ k x ^ k = x ˇ k + K k ( y k − C k x ˇ k ) \begin{aligned}K_k&=\check P_kC_k^T(C_k\check P_kC_k^T+R_k)^{-1} \\ \hat P_k&=(1-K_kC_k)\check P_k \\\hat x_k&=\check x_k+K_k(y_k-C_k\check x_k)\end{aligned} KkP^kx^k=PˇkCkT(CkPˇkCkT+Rk)−1=(1−KkCk)Pˇk=xˇk+Kk(yk−Ckxˇk)
其中, y k − C k x ˇ k y_k-C_k\check x_k yk−Ckxˇk称为更新量,指的是实际与期望观测量的误差,而卡尔曼增益则是这部分更新量对估计值的权重。
通过贝叶斯推断推导卡尔曼滤波
使用贝叶斯推断方法还能够以更简洁的方式推出卡尔曼滤波。假设 k − 1 k-1 k−1时刻的高斯先验为:
p ( x k − 1 ∣ x ˇ 0 , v 1 : k − 1 , y 0 : k − 1 ) = N ( x ^ k − 1 , P ^ k − 1 ) p(x_{k-1}|\check x_0,v_{1:k-1},y_{0:k-1})=N(\hat x_{k-1},\hat P_{k-1}) p(xk−1∣xˇ0,v1:k−1,y0:k−1)=N(x^k−1,P^k−1)
首先,对于预测部份,考虑最近时刻的输入 v k v_{k} vk,来计算 k k k时刻的先验:
p ( x k ∣ x ˇ 0 , v 1 : k , y 0 : k − 1 ) = N ( x ˇ k , P ˇ k ) p(x_k|\check x_0,v_{1:k},y_{0:k-1})=N(\check x_k,\check P_k) p(xk∣xˇ0,v1:k,y0:k−1)=N(xˇk,Pˇk)
其中:
x ˇ k = E [ x k ] = E [ A k − 1 x k − 1 + v k + w k ] = A k − 1 x ^ k − 1 + v k \check x_k=E[x_k]=E[A_{k-1}x_{k-1}+v_k+w_k]=A_{k-1}\hat x_{k-1}+v_k xˇk=E[xk]=E[Ak−1xk−1+vk+wk]=Ak−1x^k−1+vk
P ˇ k = E [ ( x k − E [ x k ] ) ( x k − E [ x k ] ) T ] = A k − 1 E [ ( x k − 1 − x ^ k − 1 ) ( x k − 1 − x ^ k − 1 ) T ] A k − 1 T + E [ w k w k t ] = A k − 1 P ^ k − 1 A k − 1 T + Q k \begin{aligned}\check P_k&=E[(x_k-E[x_k])(x_k-E[x_k])^T]\\&=A_{k-1}E[(x_{k-1}-\hat x_{k-1})(x_{k-1}-\hat x_{k-1})^T]A_{k-1}^T+E[w_kw_k^t]\\&=A_{k-1}\hat P_{k-1}A_{k-1}^T+Q_k\end{aligned} Pˇk=E[(xk−E[xk])(xk−E[xk])T]=Ak−1E[(xk−1−x^k−1)(xk−1−x^k−1)T]Ak−1T+E[wkwkt]=Ak−1P^k−1Ak−1T+Qk
然后,对于更新部分,将状态与最新一次测量(即 k k k时刻)写成联合高斯分布的形式:
p ( x k , y k ∣ x ˇ 0 , v 1 : k , y 0 : k − 1 ) = N ( [ μ x μ y ] , [ Σ x x Σ x y Σ y x Σ y y ] ) = N ( [ x ˇ k C k x ˇ k ] , [ P ˇ k P ˇ k C k T C k P ˇ k C k P ˇ k C k T + R k ] ) p(x_k,y_k|\check x_0,v_{1:k},y_{0:k-1})=N(\begin{bmatrix}\mu_x\\\mu_y\end{bmatrix},\begin{bmatrix}\Sigma_{xx}&\Sigma_{xy}\\\Sigma_{yx}&\Sigma_{yy}\end{bmatrix})=N(\begin{bmatrix}\check x_k\\C_k\check x_k\end{bmatrix},\begin{bmatrix}\check P_k&\check P_kC_k^T\\C_k\check P_k&C_k\check P_kC_k^T+R_k\end{bmatrix}) p(xk,yk∣xˇ0,v1:k,y0:k−1)=N([μxμy],[ΣxxΣyxΣxyΣyy])=N([xˇkCkxˇk],[PˇkCkPˇkPˇkCkTCkPˇkCkT+Rk])
根据高斯推断,可以得到:
p ( x k ∣ x ˇ 0 , v 1 : k , y 0 : k ) = N ( μ x + Σ x y Σ y y − 1 ( y k − μ y ) , Σ x x − Σ x y Σ y y − 1 Σ y x ) p(x_k|\check x_0,v_{1:k},y_{0:k})=N(\mu_x+\Sigma_{xy}\Sigma_{yy}^{-1}(y_k-\mu_y),\Sigma_{xx}-\Sigma_{xy}\Sigma_{yy}^{-1}\Sigma_{yx}) p(xk∣xˇ0,v1:k,y0:k)=N(μx+ΣxyΣyy−1(yk−μy),Σxx−ΣxyΣyy−1Σyx)
代入之前的结果,有:
K k = P ˇ k C k T ( C k P ˇ k C k T + R k ) − 1 P ^ k = ( 1 − K k C k ) P ˇ k x ^ k = x ˇ k + K k ( y k − C k x ˇ k ) \begin{aligned}K_k&=\check P_kC_k^T(C_k\check P_kC_k^T+R_k)^{-1} \\ \hat P_k&=(1-K_kC_k)\check P_k \\ \hat x_k&=\check x_k+K_k(y_k-C_k\check x_k)\end{aligned} KkP^kx^k=PˇkCkT(CkPˇkCkT+Rk)−1=(1−KkCk)Pˇk=xˇk+Kk(yk−Ckxˇk)
这与MAP给出的更新步骤的方程是完全一致的。
重申一遍,这件事情的根本在于使用了线性模型,且噪声和先验也都是高斯的。在这些条件下,后验概率也是高斯的,于是它的均值和模正巧是一样的。然而在使用非线性模型之后就不能保证这个性质了。
从增益最优化的角度来看卡尔曼滤波
通常来说,卡尔曼滤波是线性高斯系统下的最优解。因此,也可以从其他的角度来看卡尔曼滤波的最优特性。下面介绍其中的一个:
假设有一个估计器,形式如下:
x ^ k = x ˇ k + K k ( y k − C k x ˇ k ) \hat x_k=\check x_k+K_k(y_k-C_k\check x_k) x^k=xˇk+Kk(yk−Ckxˇk)
但是此时并不知道如何选取 K k K_k Kk的值,才能正确地衡量修正部分的权重。如果定义状态的误差为(估计值 - 真值):
e ^ k = x ^ k − x k \hat e_k=\hat x_k-x_k e^k=x^k−xk
那么有:
P ^ k = E [ e ^ k e ^ k T ] = E [ ( x ^ k − x k ) ( x ^ k − x k ) T ] = E [ ( x ˇ k + K k ( C k x k + n k − C k x ˇ k ) − x k ) ( x ˇ k + K k ( C k x k + n k − C k x ˇ k ) − x k ) T ] = E [ ( ( 1 − K k C k ) ( x ˇ k − x k ) + K k n k ) ( ( 1 − K k C k ) ( x ˇ k − x k ) + K k n k ) T ] = ( 1 − K k C k ) E [ ( x ˇ k − x k ) ( x ˇ k − x k ) T ] ( 1 − K k C k ) T + K k E [ C k C k T ] K k T = ( 1 − K k C k ) P ˇ k ( 1 − K k C k ) T + K k R k K k T = P ˇ k − K k C k P ˇ k − P ˇ k C k T K k T + K k ( C k P ˇ k C k T + R k ) K k T \begin{aligned}\hat P_k&=E[\hat e_k\hat e_k^T]\\&=E[(\hat x_k-x_k)(\hat x_k-x_k)^T]\\&=E[(\check x_k+K_k(C_kx_k+n_k-C_k\check x_k)-x_k)(\check x_k+K_k(C_kx_k+n_k-C_k\check x_k)-x_k)^T]\\&=E[((1-K_kC_k)(\check x_k-x_k)+K_kn_k)((1-K_kC_k)(\check x_k-x_k)+K_kn_k)^T]\\&=(1-K_kC_k)E[(\check x_k-x_k)(\check x_k-x_k)^T](1-K_kC_k)^T+K_kE[C_kC_k^T]K_k^T\\&=(1-K_kC_k)\check P_k(1-K_kC_k)^T+K_kR_kK_k^T \\ &=\check P_k-K_kC_k\check P_k-\check P_kC_k^TK_k^T+K_k(C_k\check P_kC_k^T+R_k)K_k^T\end{aligned} P^k=E[e^ke^kT]=E[(x^k−xk)(x^k−xk)T]=E[(xˇk+Kk(Ckxk+nk−Ckxˇk)−xk)(xˇk+Kk(Ckxk+nk−Ckxˇk)−xk)T]=E[((1−KkCk)(xˇk−xk)+Kknk)((1−KkCk)(xˇk−xk)+Kknk)T]=(1−KkCk)E[(xˇk−xk)(xˇk−xk)T](1−KkCk)T+KkE[CkCkT]KkT=(1−KkCk)Pˇk(1−KkCk)T+KkRkKkT=Pˇk−KkCkPˇk−PˇkCkTKkT+Kk(CkPˇkCkT+Rk)KkT
接下来最小均方差开始正式登场了。由于协方差矩阵的对角线元素就是方差,这样一来,把协方差矩阵的对角线元素求和,用 t r tr tr来表示这种算子,它的学名叫矩阵的迹。
于是,可以由它定义出一个代价函数:
J ( K k ) = t r ( E [ e ^ k e ^ k T ] ) = t r ( P ˇ k ) − 2 t r ( K k C k P ˇ k ) + t r ( K k ( C k P ˇ k C k T + R k ) K k T ) \begin{aligned}J(K_k)&=tr(E[\hat e_k\hat e_k^T])\\&=tr(\check P_k)-2tr(K_kC_k\check P_k)+tr(K_k(C_k\check P_kC_k^T+R_k)K_k^T)\end{aligned} J(Kk)=tr(E[e^ke^kT])=tr(Pˇk)−2tr(KkCkPˇk)+tr(Kk(CkPˇkCkT+Rk)KkT)
最小均方差就是使得 J ( K k ) J(K_k) J(Kk)最小,对未知量 K k K_k Kk求导,令导函数等于0:
d J ( K k ) d K k = − 2 ( C k P ˇ k ) T + 2 K k ( C k P ˇ k C k T + R k ) \frac{dJ(K_k)}{dK_k}=-2(C_k\check P_k)^T+2K_k(C_k\check P_kC_k^T+R_k) dKkdJ(Kk)=−2(CkPˇk)T+2Kk(CkPˇkCkT+Rk)
因此:
K k = P ˇ k C k T ( C k P ˇ k C k T + R k ) − 1 K_k=\check P_kC_k^T(C_k\check P_kC_k^T+R_k)^{-1} Kk=PˇkCkT(CkPˇkCkT+Rk)−1
这正是卡尔曼增益的通常表达式。
关于卡尔曼滤波的讨论
以下是卡尔曼滤波的要点:
- 对于高斯噪声的线性系统,卡尔曼滤波器是最优线性无偏估计;
- 必须有初始状态: { x ˇ 0 , P ˇ 0 } \{\check x_0,\check P_0\} {xˇ0,Pˇ0};
- 协方差部分与均值部分可以独立地递推。有时甚至可以计算一个固定的 K k K_k Kk,用于所有时刻的均值修正,这种做法称为固定状态的卡尔曼滤波。
相关文章:

【状态估计】线性高斯系统的状态估计——离散时间的递归滤波
前两篇文章介绍了离散时间的批量估计、离散时间的递归平滑,本文着重介绍离散时间的递归滤波。 前两篇位置:【状态估计】线性高斯系统的状态估计——离散时间的批量估计、【状态估计】线性高斯系统的状态估计——离散时间的递归平滑。 离散时间的递归滤波…...
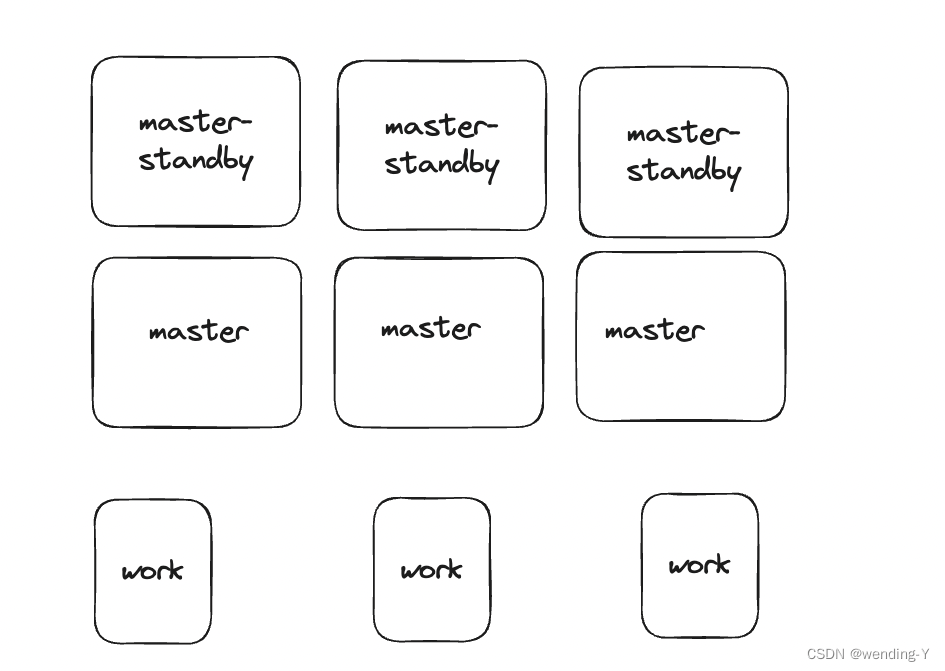
架构设计上中的master三种架构,单节点,主从节点,多节点分析
文章目录 背景单节点优点缺点 主从节点优点缺点 多节点优点缺点 多节点,多backup设计优点缺点 总结 背景 在很多分布式系统里会有master,work这种结构。 master 节点负责管理资源,分发任务。下面着重讨论下master 数量不同带来的影响 单节点 优点 1.设…...

如何在 SQL 中删除一条记录?
如何在 SQL 中删除一条记录? 在 SQL 中,您可以使用DELETE查询和WHERE子句删除表中的一条记录。在本文中,我将向您介绍如何使用DELETE查询和WHERE子句删除记录。我还将向您展示如何一次从表中删除多条记录 如何在 SQL 中使用 DELETE 这是使…...
JavaSE (Java基础):面向对象(上)
8 面向对象 面向对象编程的本质就是:以类的方法组织代码,以对象的组织(封装)数据。 8.1 方法的回顾 package com.oop.demo01;// Demo01 类 public class Demo01 {// main方法public static void main(String[] args) {int c 10…...

flink使用StatementSet降低资源浪费
背景 项目中有很多ods层(mysql 通过cannal)kafka,需要对这些ods kakfa做一些etl操作后写入下一层的kafka(dwd层)。 一开始采用的是executeSql方式来执行每个ods→dwd层操作,即类似: def main(…...

FineDataLink4.1.9支持Kettle调用
FDL更新至4.1.9后,新增kettle调用功能,支持不增加额外负担的情况下,将现有的Kettle任务平滑迁移到FineDataLink。 一、更新版本前存在的问题与痛点 在此次功能更新前,用户可能会遇到以下问题: 1.对于仅使用kettle的…...

SwanLinkOS首批实现与HarmonyOS NEXT互联互通,软通动力子公司鸿湖万联助力鸿蒙生态统一互联
在刚刚落下帷幕的华为开发者大会2024上,伴随全场景智能操作系统HarmonyOS Next的盛大发布,作为基于OpenHarmony的同根同源系统生态,软通动力子公司鸿湖万联全域智能操作系统SwanLinkOS首批实现与HarmonyOS NEXT互联互通,率先攻克基…...

Win11禁止右键菜单折叠的方法
背景 在使用windows11的时候,会发现默认情况下,右键菜单折叠了。以至于在使用一些软件的右键菜单时总是要点击“显示更多选项”菜单展开所有菜单,然后再点击。而且每次在显示菜单时先是全部展示,再隐藏一下,看着着实难…...
Maven列出所有的依赖树
在 IntelliJ IDEA 中,你可以使用 Maven 插件来列出项目的依赖树。Maven 插件提供了一个名为dependency:tree的目标,可以帮助你获取项目的依赖树详细信息。 要列出项目的依赖树,可以执行以下步骤: 打开 IntelliJ IDEA,…...

测试开发面试题和答案
Python 请解释Python中的列表推导式(List Comprehension)是什么,并给出一个示例。 答案: 列表推导式是Python中一种简洁的构建列表的方法。它允许从一个已存在的列表创建新列表,同时应用一个表达式来修改或选择元素。…...

llm学习-3(向量数据库的使用)
1:数据读取和加载 接着上面的常规操作 加载环境变量---》获取所有路径---》加载文档---》切分文档 代码如下: import os from dotenv import load_dotenv, find_dotenvload_dotenv(find_dotenv()) # 获取folder_path下所有文件路径,储存在…...
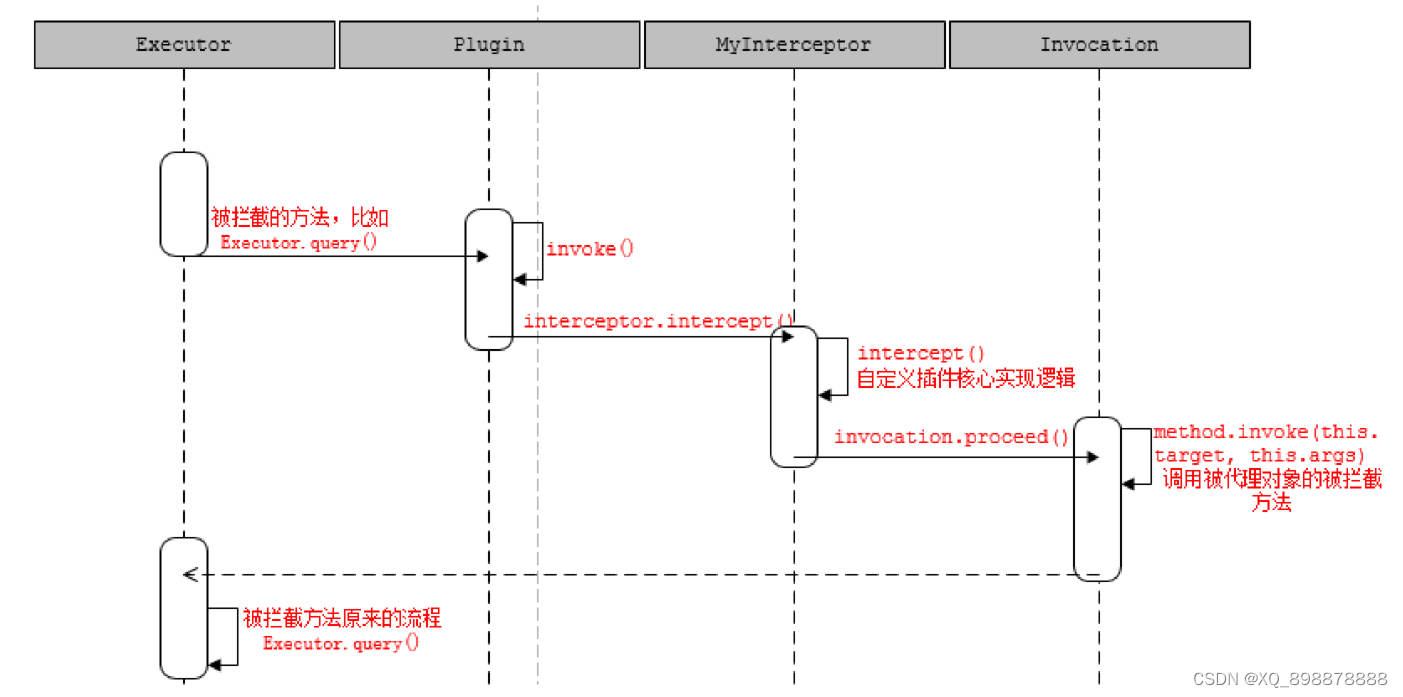
【01-02】Mybatis的配置文件与基于XML的使用
1、引入日志 在这里我们引入SLF4J的日志门面,使用logback的具体日志实现;引入相关依赖: <!--日志的依赖--><dependency><groupId>org.slf4j</groupId><artifactId>slf4j-api</artifactId><version&g…...
)
Linux-进程间通信(IPC)
进程间通信(IPC)介绍 进程间通信(IPC,InterProcess Communication)是指在不同的进程之间传播或交换信息。IPC 的方式包括管道(无名管道和命名管道)、消息队列、信号量、共享内存、Socket、Stre…...

C++ STL: std::vector与std::array的深入对比
什么是 std::vector 和 std::array 首先,让我们简要介绍一下这两种容器: • std::vector:一个动态数组,可以根据需要动态调整其大小。 • std::array:一个固定大小的数组,其大小在编译时确定。 虽然…...

哈哈看到这条消息感觉就像是打开了窗户
在这个信息爆炸的时代,每一条动态可能成为我们情绪的小小触发器。今天,当我无意间滑过那条由杜海涛亲自发布的“自曝式”消息时,不禁心头一颤——如果这是我的另一半,哎呀,那画面,简直比烧烤摊还要“热辣”…...

10、matlab中字符、数字、矩阵、字符串和元胞合并为字符串并将字符串以不同格式写入读出excel
1、前言 在 MATLAB 中,可以使用不同的数据类型(字符、数字、矩阵、字符串和元胞)合并为字符串,然后将字符串以不同格式写入 Excel 文件。 以下是一个示例代码,展示如何将不同数据类型合并为字符串,并以不…...

如何正确面对GPT-5技术突破
随着人工智能技术的快速发展,预训练语言模型在自然语言处理领域取得了显著的成果。其中,GPT系列模型作为代表之一,受到了广泛关注。2023年,GPT-5模型的发布引起了业界的热烈讨论。本文将从以下几个方面分析GPT-5的发布及其对人工智…...
HarmonyOS ArkUi 官网踩坑:单独隐藏导航条无效
环境: 手机:Mate 60 Next版本: NEXT.0.0.26 导航条介绍 导航条官网设计指南 setSpecificSystemBarEnabled 设置实际效果: navigationIndicator:隐藏导航条无效status:会把导航条和状态栏都隐藏 官方…...
)
解决跨域问题(vite、axios/koa)
两种方法选其一即可 一、后端koa设置中间件 app.use(async (ctx, next)> {ctx.set(Access-Control-Allow-Origin, *);ctx.set(Access-Control-Allow-Headers, Content-Type, Content-Length, Authorization, Accept, X-Requested-With , yourHeaderFeild);ctx.set(Access-C…...
echarts实现3D柱状图(视觉层面)
一、第一种效果 效果图 使用步骤 完整实例,copy就可直接使用 <template><div :class"className" :style"{height:height,width:width}" /> </template><script>import echarts from echartsrequire(echarts/theme/…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...
