Leetcode 3202. Find the Maximum Length of Valid Subsequence II
- Leetcode 3202. Find the Maximum Length of Valid Subsequence II
- 1. 解题思路
- 2. 代码实现
- 题目链接:3202. Find the Maximum Length of Valid Subsequence II
1. 解题思路
这一题的话是上一题3201. Find the Maximum Length of Valid Subsequence I的升级版,主要就是将除数2调整为任意正数k,但是本质上还是一样的,我们同样有奇数位和偶数位上的数必然对k有着相同的余数,此时,我们只需要考察前两个元素的余数组合,然后考察他们的所有位置能够组成的交叉序列的最大长度即可。
当前两个元素的余数相同时,我们能够获得的最大子序列的长度就是k的余数相同的元素出现的最大频次。
当前两个元素的余数不同时,我们能够快速得到两个余数的位置序列,然后我们通过贪婪算法配合二分搜索即可快速得到他们能够组成的最大交叉序列长度。
最后,如果两个序列的长度之后都小于当前已经获得的最大序列长度了,我们就可以直接跳过这些可能性了,由此,我们即可进一步对问题进行剪枝,从而得到我们最终的答案。
2. 代码实现
给出python代码实现如下:
class Solution:def maximumLength(self, nums: List[int], k: int) -> int:locs = defaultdict(list)for i, x in enumerate(nums):locs[x%k].append(i)ans = max(len(x) for x in locs.values())def get_max_length(s1, s2):n, m = len(s1), len(s2)i, j = 0, 0cnt = 1 if s2[0] < s1[0] else 0while i < n:cnt += 1j = bisect.bisect_left(s2, s1[i])if j < m:cnt += 1else:breaki = bisect.bisect_left(s1, s2[j])return cntfor i in range(k-1):if locs[i] == []:continuefor j in range(i+1, k):if len(locs[i]) + len(locs[j]) <= ans:continuecnt = get_max_length(locs[i], locs[j])ans = max(ans, cnt)return ans
提交代码评测得到:耗时277ms,占用内存16.8MB。
相关文章:

Leetcode 3202. Find the Maximum Length of Valid Subsequence II
Leetcode 3202. Find the Maximum Length of Valid Subsequence II 1. 解题思路2. 代码实现 题目链接:3202. Find the Maximum Length of Valid Subsequence II 1. 解题思路 这一题的话是上一题3201. Find the Maximum Length of Valid Subsequence I的升级版&am…...

通过Spring Boot结合实时流媒体技术对考试过程进行实时监控
本章将深入探讨考试系统中常见的复杂技术问题,并提供基于Spring Boot 3.x的解决方案。涵盖屏幕切换检测与防护、接打电话识别处理、行为监控摄像头使用、网络不稳定应对等,每篇文章详细剖析问题并提供实际案例与代码示例,帮助开发者应对挑战&…...

智能扫地机器人避障与防跌落问题解决方案
智能扫地机器人出现避障与防跌落问题时,可以通过以下几种方式来解决: 一、避障问题的解决方案 1.升级避障技术: ① 激光雷达避障:激光雷达通过发射和接收激光信号来判断与障碍物的距离,具有延迟低、效果稳定、准确度…...

德旺训练营称重问题
这是考小学的分治策略,小学的分治策略几乎都是分三组。本着这个策略,我们做看看。 第一次称重: 分三组,16,16,17,拿两个16称,得到A情况,一样重,那么假铜钱在那组17个里面。B情况不…...

数据决策系统详解
文章目录 数据决策系统的核心组成部分:1. **数据收集与整合**:2. **数据处理与分析**:3. **数据可视化**:4. **决策支持**: 数据决策系统的功能:决策类型:数据决策系统对企业的重要性࿱…...

JSON 简述与应用
1. JSON 简述 JSON(JavaScript Object Notation)是一种轻量级的数据交换格式,常用于客户端与服务器之间的数据传递。它基于JavaScript对象表示法,但独立于语言,可以被多种编程语言解析和生成。 1.1 特点 轻量级&#…...

ResNet50V2
🍨 本文为🔗365天深度学习训练营 中的学习记录博客🍖 原作者:K同学啊 一、ResNetV1和ResNetV2的区别 ResNetV2 和 ResNetV1 都是深度残差网络(ResNet)的变体,它们的主要区别在于残差块的设计和…...

基于深度学习的虚拟换装
基于深度学习的虚拟换装技术旨在通过计算机视觉和图像处理技术,将不同的服装虚拟地穿在用户身上,实现快速的试穿和展示。这项技术在电商、时尚和虚拟现实领域具有广泛的应用,能够提升用户体验,增加互动性。以下是关于这一领域的系…...

单段时间最优S型速度规划算法
一,背景 在做机械臂轨迹规划的单段路径的速度规划时,除了参考《Trajectory Planning for Automatic Machines and Robots》等文献之外,还在知乎找到了这位大佬 韩冰 写的在线规划方法: https://zhuanlan.zhihu.com/p/585253101/e…...

pom文件-微服务项目结构
一、微服务项目结构 my-microservices-project/ ├── pom.xml <!-- 父模块的pom.xml --> ├── ry-system/ │ ├── pom.xml <!-- 子模块ry-system的pom.xml --> │ └── src/main/java/com/example/rysystem/ │ └── RySystemApplication.…...

解析Kotlin中的Nothing【笔记摘要】
1.Nothing的本质 Nothing 的源码很简单: public class Nothing private constructor()可以看到它是个class,但它的构造函数是 private 的,这就导致我们没法创建它的实例,并且在源码里 Kotlin 也没有帮我们创建它的实例。 基于这…...

toRefs 和 toRef
文章目录 toRefs 和 toReftoRefstoRef toRefs 和 toRef toRefs toRefs 把一个由reactive对象的值变为一个一个ref的响应式的值 import { ref, reactive, toRefs, toRef } from vue; let person reactive({name: 张三,age: 18, }); // toRefs 把一个由reactive对象的值变为一…...
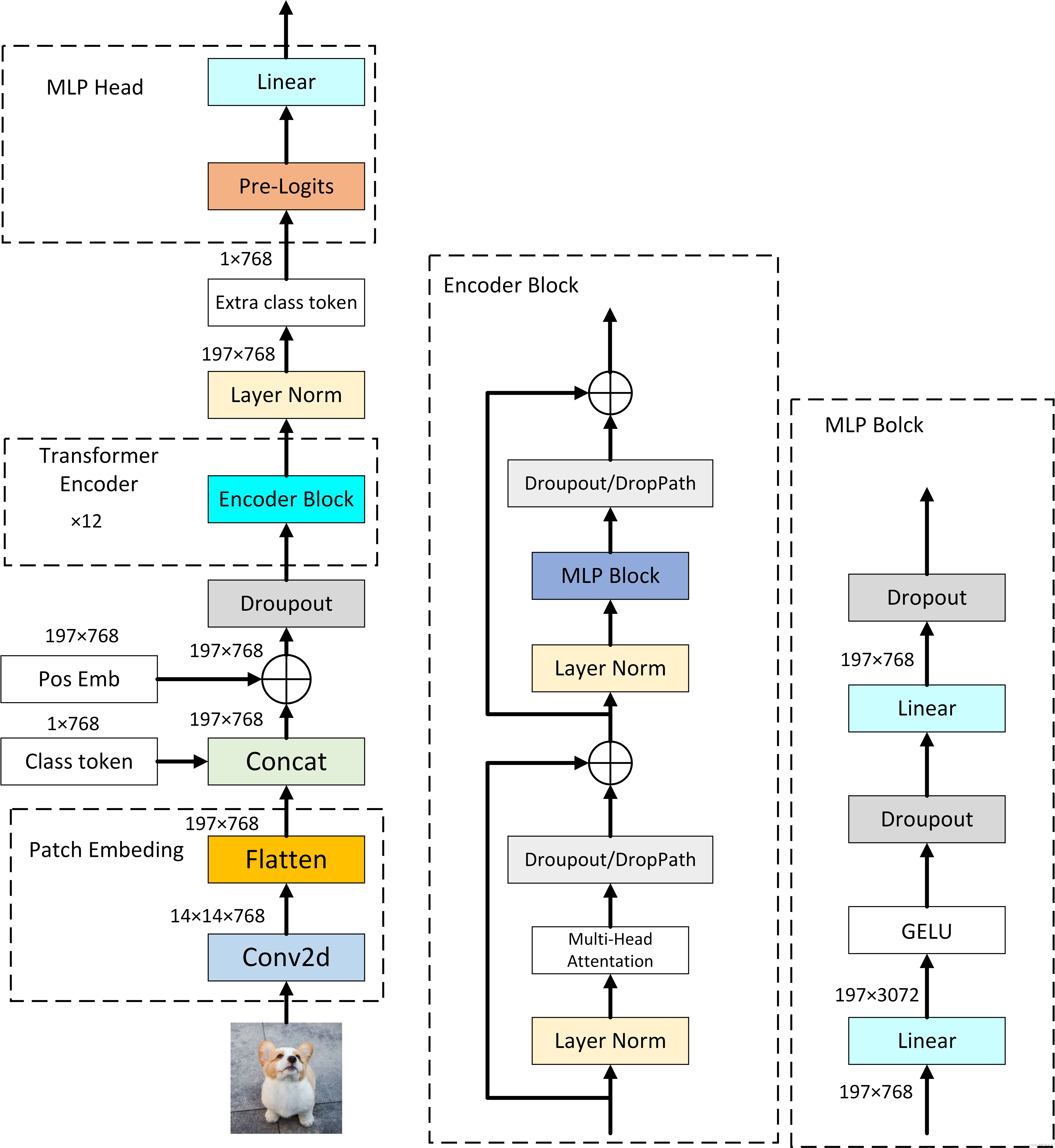
Vision Transformer论文阅读笔记
目录 An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale -- Vision Transformer摘要Introduction—简介RELATED WORK—相关工作METHOD—方法VISION TRANSFORMER (VIT)—视觉Transformer(ViT) 分析与评估PRE-TRAINING DATA REQUIREMENTS—预训练数据…...

MapReduce的执行流程排序
MapReduce 是一种用于处理大规模数据集的分布式计算模型。它将作业分成多个阶段,以并行处理和分布式存储的方式来提高计算效率。以下是 MapReduce 的执行流程以及各个阶段的详细解释: 1. 作业提交(Job Submission) 用户通过客户端…...

雅思词汇及发音积累 2024.7.3
银行 check (美)支票 cheque /tʃek/ (英)支票 ATM 自动取款机 cashier 收银员 teller /ˈtelə(r)/ (银行)出纳员 loan 贷款 draw/withdraw money 提款 pin number/passsword/code …...

Vue2和Vue3的区别Vue3的组合式API
一、Vue2和Vue3的区别 1、创建方式的不同: (1)、vue2:是一个构造函数,通过该构造函数创建一个Vue实例 new Vue({})(2)、Vue3:是一个对象。并通过该对象的createApp()方法,创建一个vue实例。 Vue…...

ML307R OpenCPU HTTP使用
一、函数介绍 二、示例代码 三、代码下载地址 一、函数介绍 具体函数可以参考cm_http.h文件,这里给出几个我用到的函数 1、创建客户端实例 /*** @brief 创建客户端实例** @param [in] url 服务器地址(服务器地址url需要填写完整,例如(服务器url仅为格式示…...

【状态估计】线性高斯系统的状态估计——离散时间的递归滤波
前两篇文章介绍了离散时间的批量估计、离散时间的递归平滑,本文着重介绍离散时间的递归滤波。 前两篇位置:【状态估计】线性高斯系统的状态估计——离散时间的批量估计、【状态估计】线性高斯系统的状态估计——离散时间的递归平滑。 离散时间的递归滤波…...
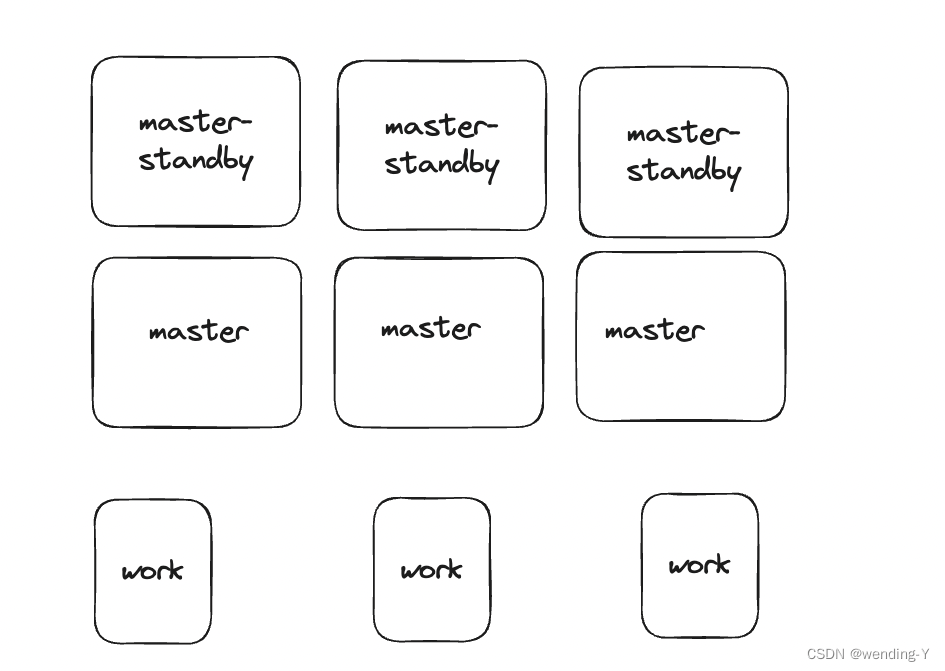
架构设计上中的master三种架构,单节点,主从节点,多节点分析
文章目录 背景单节点优点缺点 主从节点优点缺点 多节点优点缺点 多节点,多backup设计优点缺点 总结 背景 在很多分布式系统里会有master,work这种结构。 master 节点负责管理资源,分发任务。下面着重讨论下master 数量不同带来的影响 单节点 优点 1.设…...

如何在 SQL 中删除一条记录?
如何在 SQL 中删除一条记录? 在 SQL 中,您可以使用DELETE查询和WHERE子句删除表中的一条记录。在本文中,我将向您介绍如何使用DELETE查询和WHERE子句删除记录。我还将向您展示如何一次从表中删除多条记录 如何在 SQL 中使用 DELETE 这是使…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...

对象回调初步研究
_OBJECT_TYPE结构分析 在介绍什么是对象回调前,首先要熟悉下结构 以我们上篇线程回调介绍过的导出的PsProcessType 结构为例,用_OBJECT_TYPE这个结构来解析它,0x80处就是今天要介绍的回调链表,但是先不着急,先把目光…...

[拓扑优化] 1.概述
常见的拓扑优化方法有:均匀化法、变密度法、渐进结构优化法、水平集法、移动可变形组件法等。 常见的数值计算方法有:有限元法、有限差分法、边界元法、离散元法、无网格法、扩展有限元法、等几何分析等。 将上述数值计算方法与拓扑优化方法结合&#…...

FOPLP vs CoWoS
以下是 FOPLP(Fan-out panel-level packaging 扇出型面板级封装)与 CoWoS(Chip on Wafer on Substrate)两种先进封装技术的详细对比分析,涵盖技术原理、性能、成本、应用场景及市场趋势等维度: 一、技术原…...

Vue 实例的数据对象详解
Vue 实例的数据对象详解 在 Vue 中,数据对象是响应式系统的核心,也是组件状态的载体。理解数据对象的原理和使用方式是成为 Vue 专家的关键一步。我将从多个维度深入剖析 Vue 实例的数据对象。 一、数据对象的定义方式 1. Options API 中的定义 在 Options API 中,使用 …...
