算法-位图与底层运算逻辑
文章目录
- 1. 位图的理论基础
- 2. 完整版位图实现
- 3. 底层的运算逻辑-位运算
1. 位图的理论基础
首先我们要理解什么是位图, 位图的一些作用是什么
位图法就是bitmap的缩写。所谓bitmap,就是用每一位来存放某种状态,适用于大规模数据,但数据状态又不是很多的情况。通常是用来判断某个数据存不存在的。在cpp中的STL中有一个bitset容器,其实就是位图法。其实就是一种为了减少空间而存在存储数字的一种数据结构
其实学习了位图之后, 我更愿意称之为"位映射"
我们基础的位图结构包含下面的几种方法
- add方法(向位图中添加该数字)
- remove方法(在位图中删除该数字)
- reverse/flip方法(在位图中将该位的数字状态进行翻转)
- contains方法(检查位图中是否有这个数字)
下面是位图存储原理的分析

位图可以存储 0 ~ n 范围内的数字, 上面线段表示每一个整数的范围, 一个整数有32个比特位, 所以一个整数可以存储32个整数的状态, 比如第一个整数存储数据的范围是[0,31],第二个是[32,63], 以此类推…, 记住这里面有一个小点就是我们a / b向上取整的代码实现是 (a + b - 1) / b
下面是基础版本位图的实现
/*** 位图是一种在指定的连续的范围上替代哈希表来存储数字数据的一种数据结构* 构造方法是传入一个数字n, 可以实现从 [0 , n - 1]范围上数字的查询(n个数字)* 数字所需的位置在 set[n / 32] , 数字的指定的位数在 n % 32 (从最右侧开始,起始为0)*/
class BitsSet {int[] set;public BitsSet(int n) {//容量需要进行向上的取整, 可以用数学工具类中的ceiling方法进行向上的取整, 也可以用这个表达式// a / b 向上取整的结果是 (a + b - 1) / bthis.set = new int[(n + 31) / 32];}/*** add方法*/public void add(int n) {set[n / 32] = set[n / 32] | (1 << (n % 32));}/*** remove方法(思考为什么用取反不用异或)*/public void remove(int n) {set[n / 32] = set[n / 32] & (~(1 << (n % 32)));}/*** reverse/flip方法(如果有这个数字就remove,如果没有就add)*/public void reverse(int n) {set[n / 32] = set[n / 32] ^ (1 << (n % 32));}/*** contains方法(检查是不是有这个数字)*/public boolean contains(int n) {return ((set[n / 32] >>> (n % 32)) & 1) == 1;}
}2. 完整版位图实现

上面这个leetcode对位图的完整版的实现, 我们来解析一下这个位图的具体方法, 其中fix方法就是基础版本位图的add方法, unfix其实就是remove方法, flip是一个反转的方法, 可能很多人觉得真的要将位图中的所有的元素的状态都进行翻转, 其实没有必要, 而且如果全部都进行反转是十分消耗资源的, 我们直接采用一种假翻转的状态, 即定义一个布尔类型变量reverse来判断位图的元素是否进行了翻转, 反转之前我们的0代表不存在, 1代表存在, 翻转之后我们的1代表不存在, 0代表存在, 我们基本属性有set(位图的主体), one(1的个数), zero(0的个数), size(元素数量), reverse(是否进行翻转), 这里很有意思, 我们实现的filp方法直接把 reverse = !reverse , zero跟one 的数值交换即可, 就已经实现了我们的交换的目的, 其实这是一种假交换, 代码如下图所示
/*** 自己实现一个完整版本的位图*/
class Bitset {//基本的数据集合private int[] set;//数据的个数private int size;//1的个数(注意在我们这里不是真实的二进制1的个数)private int one;//0的个数(注意在我们这里不是真实的二进制0的个数)private int zero;//判断该bits是否进行了翻转private boolean reverse;public Bitset(int size) {this.size = size;set = new int[(size + 31) / 32];zero = size;one = 0;reverse = false;}public void fix(int idx) {int index = idx / 32;int bit = idx % 32;if (!reverse) {//说明没有进行翻转, 此时0表示不存在1表示存在if ((set[index] & (1 << bit)) == 0) {one++;zero--;set[index] = set[index] | (1 << bit);}} else {//此时说明已经进行了翻转操作if ((set[index] & (1 << bit)) != 0) {one++;zero--;set[index] = set[index] & (~(1 << bit));}}}public void unfix(int idx) {int index = idx / 32;int bit = idx % 32;if (!reverse) {//此时说明没有发生翻转, 此时0表示不存在1表示存在if ((set[index] & (1 << bit)) != 0) {one--;zero++;set[index] = set[index] & (~(1 << bit));}} else {if ((set[index] & (1 << bit)) == 0) {one--;zero++;set[index] = set[index] | (1 << bit);}}}public void flip() {reverse = !reverse;zero = zero ^ one;one = zero ^ one;zero = zero ^ one;}public boolean all() {return size == one;}public boolean one() {return one > 0;}public int count() {return one;}//其实就是重写一下toString方法@Overridepublic String toString() {StringBuilder sbd = new StringBuilder();int index = 0;while (index < size) {int num = set[index / 32];for (int j = 0; j < 32 && index < size; j++) {if (!reverse) {if (((num >>> j) & 1) == 1) {sbd.append(1);} else {sbd.append(0);}index++;} else {if (((num >>> j) & 1) == 1) {sbd.append(0);} else {sbd.append(1);}index++;}}}return sbd.toString();}
}3. 底层的运算逻辑-位运算
其实计算机的底层实现加减乘除的时候是没有 + - * / 这些符号的区分的, 其实底层的运算的逻辑都是使用位运算拼接出来的…
3.1 加法
首先阐释一下加法的运算的原理就是 加法的结果 = 无进位相加的结果( ^ ) + 进位信息( & 与 << ),当进位信息为 0 的时候, 那个无尽为相加的结果, 也就是异或运算的结果就是答案

代码实现如下(不懂得看我们位运算的基础中关于异或运算的理解)
//因为是进位信息, 所以获得完了之后要左移一位
public static int add(int a, int b) {int ans = a;while (b != 0) {//ans更新为无尽无进位相加的结果ans = a ^ b;//b更新为进位信息b = (a & b) << 1;a = ans;}return ans;}
3.2 减法
减法得实现更加得简答, 就是把我们的 a - b ⇒ a + (-b), 转换为加法进行操作, 代码实现如下
/*** 生成一个数相反数的方法* 之前我们学过的那个 Brain Kernighan算法中有一个就是 -n == (~n + 1)* 所以计算相反数其实就是 add(~n , 1)*/public static int neg(int n) {return add(~n, 1);}/*** 减法的运算结果其实就是把 减法转换为加法 比如 a - b = a + (-b);*/public static int sub(int a, int b) {return add(a, neg(b));}
3.3 乘法
乘法的计算方式本质上是类比的我们小学的时候学习的竖式乘法
也就是说, 乘法的本质实现还是依赖的加法, 代码实现如下
/*** 乘法的计算方式本质上是类比的我们小学的时候学习的竖式乘法* 也就是说, 乘法的本质实现还是依赖的加法*/public static int mul(int a, int b) {int ans = 0;while (b != 0) {if ((b & 1) == 1) {ans = add(ans, a);}//这里的b一定要是无符号右移(为了避开负数)b = b >>> 1;a = a << 1;}return ans;}
3.4 除法
首先介绍得除法的基本逻辑
位运算实现除法(基础的逻辑, 但是不完备)
这个是最特殊的位运算的题目, 因为我们要考虑除数与被除数的正负关系(全部都先转化为正数进行运算)
由于整数的第 31 位是符号位, 所以我们不进行考虑(全部处理为非负), 从30进行考虑
除法的基本逻辑就是 判断一个数里面是否包含 2^i 次方
x >= y * (2^i), 也就是x的i位是1, 反之就是0, 然后让 x - y * (2^i) ; 重复此过程直至判断到最后一位(0位)
所以代码的基本逻辑就是 x >= y << i ; 但是左移可能会溢出, 所以我们改为右移 ==> (x >> i) >= y;
还有一点就是注意这里一定要先把 a b 赋值给 x y 再进行操作, 否则可能会导致后续的 a b 值发生改变影响结果判断
代码实现如下
public static int div(int a, int b) {//先把 a , b 处理为非负的int x = a < 0 ? neg(a) : a;int y = b < 0 ? neg(b) : b;int ans = 0;for (int i = 30; i >= 0; i = sub(i, 1)) {if ((x >> i) >= y) {ans = ans | (1 << i);//这一步为什么不会溢出其实我暂时也没懂, 先记下来吧x = sub(x, y << i);}}//注意这里的异或运算也可以作用与布尔类型, 其本质就是0 / 1进行的异或运算return a < 0 ^ b < 0 ? neg(ans) : ans;}
下面的这个才是除法的正确逻辑, 相关注释在代码中体现
下面这个才是相对完备的逻辑, 对一些特殊情况进行了处理, 因为除数与被除数有可能没有相反数(整数最小值越界)
public static final int MIN = Integer.MIN_VALUE;public static int divide(int dividend, int divisor) {//同时是最小值if (dividend == MIN && divisor == MIN) {return -1;}//同时都不是最小值(基本的除法逻辑)if (dividend != MIN && divisor != MIN) {return div(dividend, divisor);}//代码执行到这里就说明二者中必有一个是最小值, 另一个不是, 此时需要判断除数是不是-1, 判断会不会越界if(divisor == neg(1)){return Integer.MAX_VALUE;}if(divisor == MIN){return 0;}//代码走到这里就只剩下了一种情况, 就是divisor不是-1, dividend是最小值//此时你直接运算取反肯定会溢出, 所以此时进行一些变换操作, 此时(a + b)/(a - b)不会溢出//1. b为正数 , a / b == (a + b - b) / b ==> ((a + b) / b) - 1;//2. b为负数 , a / b == (a - b + b) / b ==> ((a - b) / b) + 1;dividend = add(dividend, divisor < 0 ? neg(divisor) : divisor);int ans = div(dividend,divisor);int offset = divisor > 0 ? neg(1) : 1;return add(ans,offset);}
上面除法的一些标准来源于leetcode29计算除法

谢谢观看
相关文章:

算法-位图与底层运算逻辑
文章目录 1. 位图的理论基础2. 完整版位图实现3. 底层的运算逻辑-位运算 1. 位图的理论基础 首先我们要理解什么是位图, 位图的一些作用是什么 位图法就是bitmap的缩写。所谓bitmap,就是用每一位来存放某种状态,适用于大规模数据,但数据状态又…...
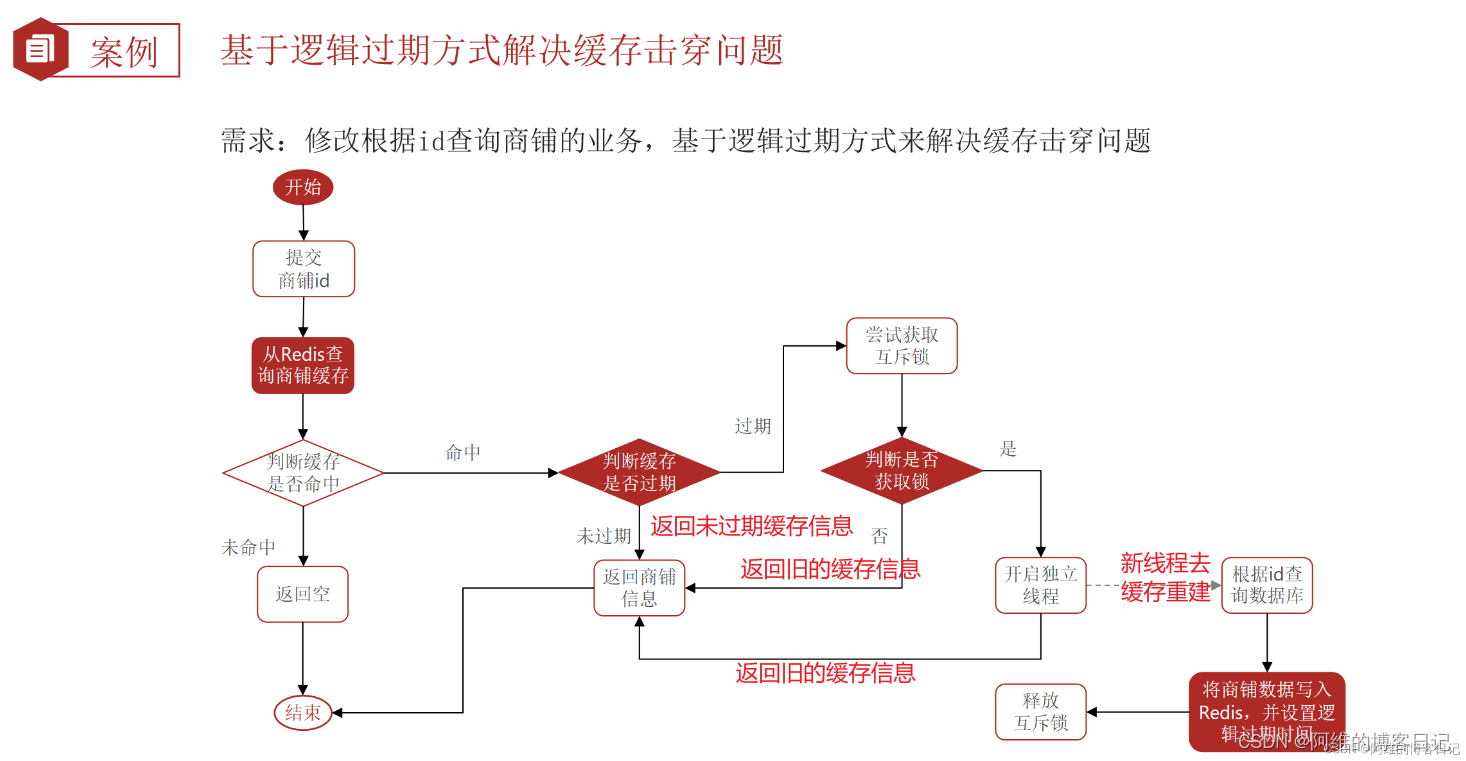
黑马点评-Redis的缓存击穿,缓存雪崩,缓存穿透,互斥锁,逻辑过期
文章目录 1.缓存穿透2.缓存雪崩3.缓存击穿3.1 互斥锁3.2 基于逻辑过期 1.缓存穿透 解决办法 写入NULL值到Redis缓存,以后就会命中Redis的控制缓存而不会出现请求直接打到数据库的问题! 代码 2.缓存雪崩 这个概念很好理解,雪崩就是无数的…...

8624 多项式系数累加和
这个问题可以通过使用数学的导数规则来解决。对于一个多项式,它的导数可以通过将每一项的系数乘以它的指数,然后降低该项的指数来得到。这个过程可以重复M次来得到多项式的M阶导数。然后,我们可以简单地将所有项的系数相加来得到结果。 以下…...

使用 C# 和 OpenXML 读取大型 Excel 文件
介绍 高效读取大型 Excel 文件可能具有挑战性,尤其是在处理需要高性能和可扩展性的应用程序时。Microsoft 的 OpenXML SDK 提供了一套强大的工具来处理 Office 文档(包括 Excel 文件),而无需在服务器上安装 Excel。本文将指导您使…...

【基于R语言群体遗传学】-5-扩展到两个以上等位基因及多基因位点
我们现在继续对于群体遗传学进行统计建模,书接上回,我们讨论了孤雌生殖的物种违反哈代温伯格遗传比例的例子,那我们现在来看多于两个等位基因的情况的计算。 如果没有看过之前文章的同学,可以先去看一下之前的文章: …...
是什么?)
重采样(上采样或下采样)是什么?
重采样(Resampling)是在数据处理中常用的一种技术,主要用于处理数据集中的不平衡问题。具体来说,重采样可以分为上采样(Oversampling)和下采样(Undersampling),它们分别是…...
)
AI与Python共舞:如何利用深度学习优化推荐系统?(2)
推荐系统的前世今生 推荐系统的历史可以追溯到20世纪90年代,从最初的基于内容过滤和协同过滤,到现在融合了机器学习甚至是深度学习的混合型推荐,其目标始终如一:更精准、更个性化地为用户推荐内容。随着Python的普及,…...

ChatGPT:Java中的对象引用实现方式
ChatGPT:Java中的对象引用实现方式 如果使用句柄的话,那么 Java 堆中将会划分出一块内存来作为句柄池,reference 中存储的就是对象的句柄地址,而句柄中包含了对象实例数据与对象类型数据各自的具体地址信息。 你提到的句柄机制是…...
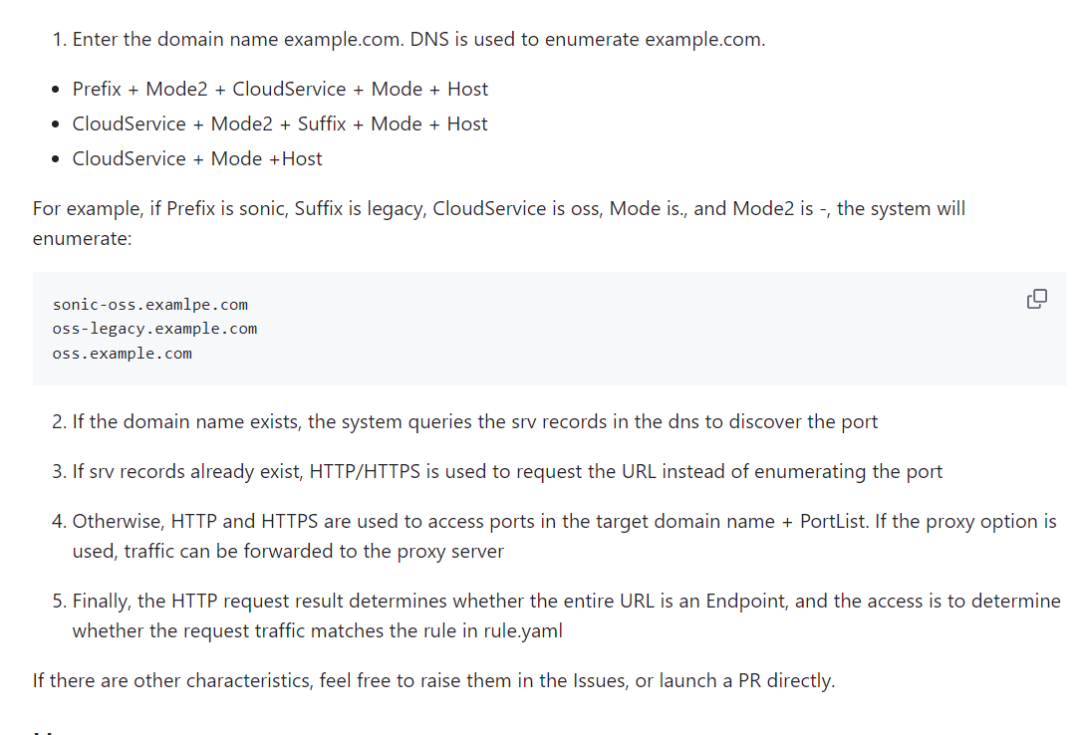
云渗透实战手册:云API攻防之云服务端点侦查
在云计算环境中的渗透,与传统渗透相比,新增加了许多新的攻击面,同时也因为云计算的特点我们需要转变渗透的思维,用云计算的方式去思考云渗透。 基础知识 在云渗透开始之前,我们需要首先阐述标题中提到的云服务端点概…...

PHP 爬虫之使用 Curl库抓取淘宝商品列表数据网页的方法
使用 PHP 的 cURL 库来抓取淘宝商品列表数据网页需要谨慎,因为淘宝等电商平台通常会有反爬虫机制,以防止数据被滥用。然而,如果你只是出于学习目的,并且了解并遵守了淘宝的robots.txt文件和相关的使用条款,你可以尝试使…...
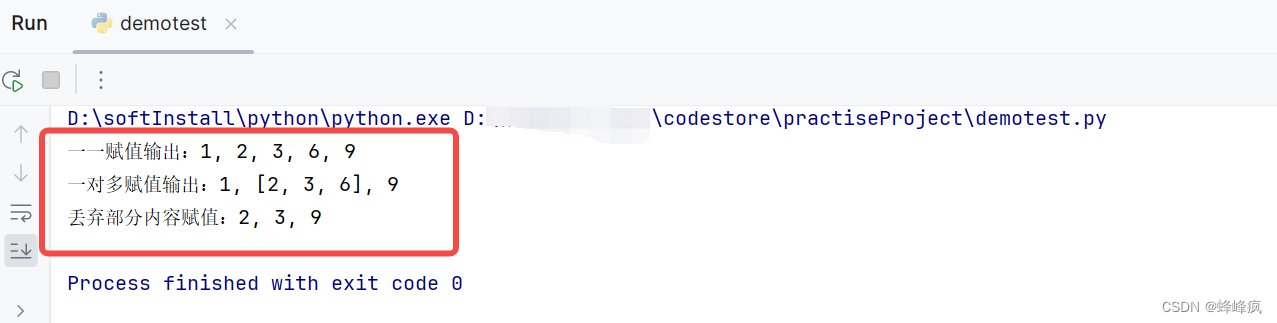
Python基础小知识问答系列-可迭代型变量赋值
1. 问题: 怎样简洁的把列表中的元素赋值给单个变量? 当需要列表中指定几个值时,剩余的变量都收集在一起,该怎么进行变量赋值? 当只需要列表中指定某几个值,其他值都忽略时,该怎么…...

主流 Canvas 库对比:Fabric.js、Konva.js 和 Pixi.js
在前端开发中,HTML5 Canvas 是一个强大的工具,可以用来创建图形、动画和各种视觉效果。为了简化和增强 Canvas 的使用,社区中出现了许多库。本文将对比三种主流的 Canvas 库:Fabric.js、Konva.js 和 Pixi.js,分析它们的…...

backbone是什么?
在深度学习中,特别是计算机视觉领域,"backbone"(骨干网络)是指用于提取特征的基础网络。它通常是卷积神经网络(CNN),其任务是从输入图像中提取高层次特征,这些特征然后被用…...

四十篇:内存巨擘对决:Redis与Memcached的深度剖析与多维对比
内存巨擘对决:Redis与Memcached的深度剖析与多维对比 1. 引言 在现代的系统架构中,内存数据库已经成为了信息处理的核心技术之一。这类数据库系统的高效性主要来源于其对数据的即时访问能力,这是因为数据直接存储在RAM中,而非传统…...
HTML5的多线程技术:Web Worker API
Web Workers API 是HTML5的一项技术,它允许在浏览器后台独立于主线程运行脚本,即允许进行多线程处理。这对于执行密集型计算任务特别有用,因为它可以防止这些任务阻塞用户界面,从而保持网页的响应性和交互性。Web Workers在自己的…...
Java | Leetcode Java题解之第206题反转链表
题目: 题解: class Solution {public ListNode reverseList(ListNode head) {if (head null || head.next null) {return head;}ListNode newHead reverseList(head.next);head.next.next head;head.next null;return newHead;} }...

660错题
不能局部求导,局部洛必达...
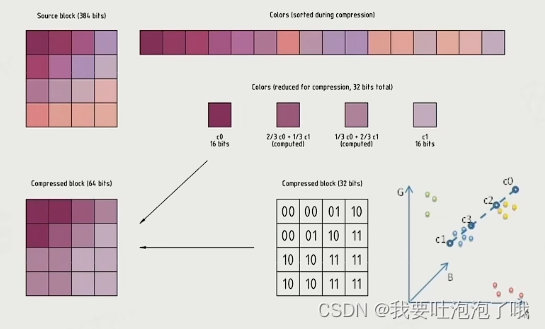
GAMES104:04游戏引擎中的渲染系统1:游戏渲染基础-学习笔记
文章目录 概览:游戏引擎中的渲染系统四个课时概览 一,渲染管线流程二,了解GPUSIMD 和 SIMTGPU 架构CPU到GPU的数据传输GPU性能限制 三,可见性Renderable可渲染对象提高渲染效率Visibility Culling 可见性裁剪 四,纹理压…...
Visual Studio 中的键盘快捷方式
1. Visual Studio 中的键盘快捷方式 1.1. 可打印快捷方式备忘单 1.2. Visual Studio 的常用键盘快捷方式 本部分中的所有快捷方式都将全局应用(除非另有指定)。 “全局”上下文表示该快捷方式适用于 Visual Studio 中的任何工具窗口。 生成࿱…...

K8S中的某个容器突然出现内存和CPU占用过高的情况解决办法
当K8S中的某个容器突然出现内存和CPU占用过高的情况时,可以采取以下步骤进行处理: 观察和分析: 使用kubectl top pods命令查看集群中各个Pod的CPU和内存占用情况,找出占用资源高的Pod。使用kubectl describe pod <pod-name>…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...

MySQL 部分重点知识篇
一、数据库对象 1. 主键 定义 :主键是用于唯一标识表中每一行记录的字段或字段组合。它具有唯一性和非空性特点。 作用 :确保数据的完整性,便于数据的查询和管理。 示例 :在学生信息表中,学号可以作为主键ÿ…...
