Halcon支持向量机
一 支持向量机
1 支持向量机介绍:
支持向量机(Support Vector Machine,SVM)是Corinna Cortes和Vapnik于1995年首先提出的,它在解决小样本、非线性及高维模式识别表现出许多特有的优势。
2 支持向量机原理:
在n维空间中找到一个分类超平面,将空间上的点分类,虚线上的点叫做支持向量机Supprot Verctor,中间红线叫超级平面,SVM目的是拉大所有点到超级平面的距离。
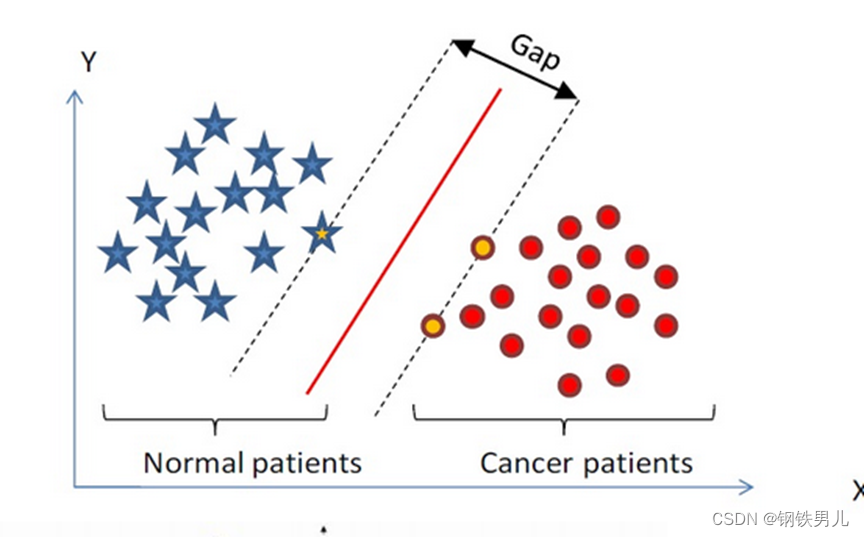
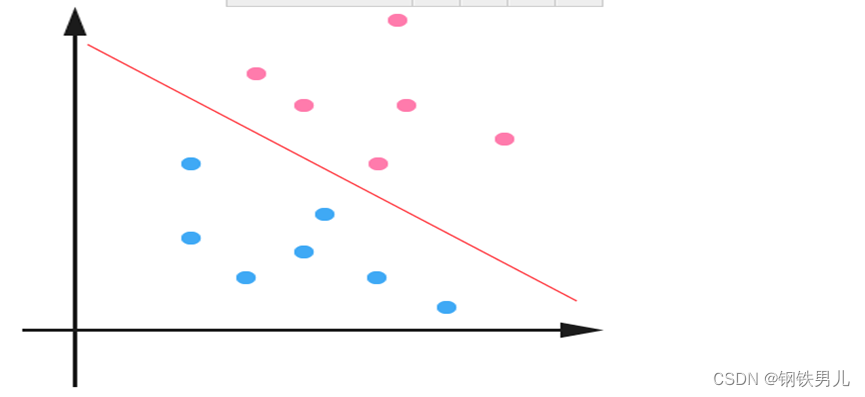
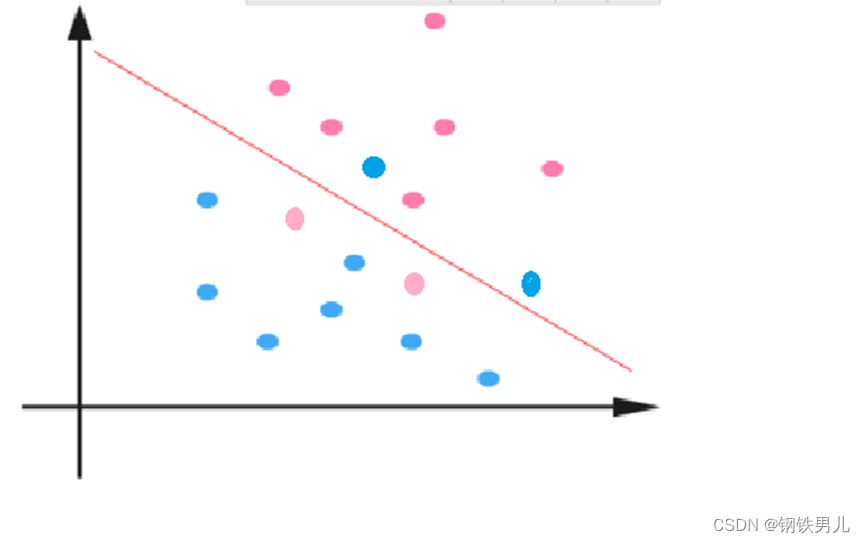
对于线性不可分的情况,我们的常用做法是把样本特征映射到高维空间中去。
但映射到高维空间,可能会导致维度太大,导致计算复杂。这里又引入核函数;
核函数:又叫非线性映射,它是将样本特征映射到高维空间,在这个空间构造最优的超平面.
核函数类型:线性核,多项式核,高斯核(rbf)等等。
正则常数C:指的是SVM里拉格朗日乘数的约束程度


正则常数值越大表示惩罚越大,越不能容忍错误,支持向量就越多,容易造成过度拟合。
正则常数越小与之相反,容易造成欠拟合.
3 SVM几种模式
one-versus-all(一对多法):训练时依次把某个类别的样本归为一类,其他剩余的样本归为另一类,这样n个类别的样本就构造出了n个SVM.
one-versus-one(一对一法):训练时依次把任意两类样本之间设计一个SVM,因此n个类别的样本就需要设计n(n-1)/2个SVM.
4 特征向量预处理类型:
canonical_variates:典型关联分析,在线性回归中,我们使用直线来拟合样本点,寻找n维特征向量X和输出结果Y之间的线性关系;
Principal component analysis:主成分分析,主成分分析(PCA)是一种统计过程,它使用一个正交变换,将一组可能的相关变量的观测值成一组线性不相关变量称为主成分的值;
相关文章:

Halcon支持向量机
一 支持向量机 1 支持向量机介绍: 支持向量机(Support Vector Machine,SVM)是Corinna Cortes和Vapnik于1995年首先提出的,它在解决小样本、非线性及高维模式识别表现出许多特有的优势。 2 支持向量机原理: 在n维空间中找到一个分类超平面…...
【Python机器学习】模型评估与改进——在模型选择中使用评估指标
我们通常希望,在使用GridSearchCV或cross_val_score进行模型选择时能够使用AUC等指标。scikit-learn提供了一种非常简单的实现方法,那就是scoring参数,它可以同时用于GridSearchCV和cross_val_score。你只需要提供一个字符串,用于…...

【C语言】union 关键字
在C语言中,union关键字用于定义联合体。联合体是一种特殊的数据结构,它允许不同的数据类型共享同一段内存。所有联合体成员共享同一个内存位置,因此联合体的大小取决于其最大成员的大小。 定义和使用联合体 基本定义 定义一个联合体类型时…...

电脑回收站删除的文件怎么恢复?5个恢复方法详解汇总!
电脑回收站删除的文件怎么恢复?在我们日常使用电脑的过程中,难免会遇到误删文件的情况。一旦发现自己误删文件了,先不要着急,还是有很多方法可以找回的。市面上还是有很多好用的文件恢复软件可以使用,具体介绍如下。 本…...

mac 安装cnpm 淘宝镜像记录
mac 安装cnpm 淘宝镜像记录 本文介绍了在安装cnpm时遇到权限问题的解决方案,包括使用sudo,处理SSL证书过期,以及因版本不一致导致的错误处理方法,步骤包括设置npm配置、卸载和重新安装cnpm到特定版本。 安装 npm install cnpm …...
编辑 11 撤销重做)
ArcGIS Pro SDK (七)编辑 11 撤销重做
ArcGIS Pro SDK (七)编辑 11 撤销&重做 文章目录 ArcGIS Pro SDK (七)编辑 11 撤销&重做1 撤消/重做最近的操作 环境:Visual Studio 2022 .NET6 ArcGIS Pro SDK 3.0 1 撤消/重做最近的操作 //撤销 if (MapV…...

Excel 中的元素定位:相对定位、绝对定位和混合定位
在Excel中,单元格引用有三种主要类型:相对定位、绝对定位和混合定位。 这些类型主要用于公式和函数中,决定在复制或拖动公式时引用如何变化。 1. 相对定位 相对定位指的是不带“$”符号的单元格引用,例如 A1。 这种引用方式在…...

Idea2024安装后点击无响应
问题 最近因工作需要,升级一下 idea 版本,之前一直使用的是2020版本,下载最新的2024版本(下载的 zip 包免安装模式,之前使用的2020版本也是免安装的,因为是免安装的,所以之前的版本也没有删除&…...

如何提高实验室分析结果的准确性呢
要提高实验室分析结果的准确性,可以从以下几个方面着手: 1、选择合适的实验方法 不同的实验方法具有不同的优缺点,实验方法的准确度直接影响测定结果的准确度。因此,在选择实验方法时,需要根据实验目的、实验原理、实…...

Perl 格式化输出:提升代码可读性的技巧
引言 Perl 是一种功能强大的脚本语言,广泛用于文本处理、系统管理、网络编程等多个领域。在 Perl 编程中,代码的格式化输出不仅有助于提升代码的可读性,还能增强程序的用户体验。本文将详细介绍如何在 Perl 中实现代码的格式化输出。 Perl …...

JavaScript基础-函数(完整版)
文章目录 函数基本使用函数提升函数参数arguments对象(了解)剩余参数(重点)展开运算符(...) 逻辑中断函数参数-默认参数函数返回值-return作用域(scope)全局作用域局部作用域变量的访问原则垃圾回收机制闭包 匿名函数函数表达式立即执行函数 箭头函数箭头…...

AI开发者的新选择:Mojo编程语言
随着人工智能技术的迅猛发展,编程语言的选择在AI项目的成功中扮演着至关重要的角色。近年来,Mojo编程语言作为一种专为AI开发者设计的新兴语言,逐渐引起了广泛关注。本文将详细介绍Mojo编程语言的特点、优势及其在AI开发中的应用。 目录 Mo…...
系统分析师--论软件开发模型及应用)
软考(高项)系统分析师--论软件开发模型及应用
文章目录 前言一、前期准备:二、论文部分: 前言 本文对系统分析师,软件开发模型及其应用文章进行展示,可以拷贝后直接粘贴到word 文档中。 一、前期准备: 项目主体功能项目背景常用的软件开发模型:瀑布模型ÿ…...

同一天提档又撤档!电影《野孩子》宣布取消7月10日公映安排——浔川电影报
同一天提档又撤档! 7月3日晚上10点,电影野孩子 发声明官宣撤档,“由于后期进度原因,电影《野孩子》将取消7月10日的公映安排,我们向各影管院线的同仁及所有观众朋友们致以最诚挚的歉意,谢谢大家这段时间的…...

Shell编程之免交互
一、Here Document免交互 1:概述 Here Document 是一个特殊用途的代码块,它在 Linux Shell 中使用 I/O 重定向的方式将命令列表提供给交互式程序或命令,比如 ftp、cat 或 read 命令,Here Document 是标准输入的一种替代品 语法…...
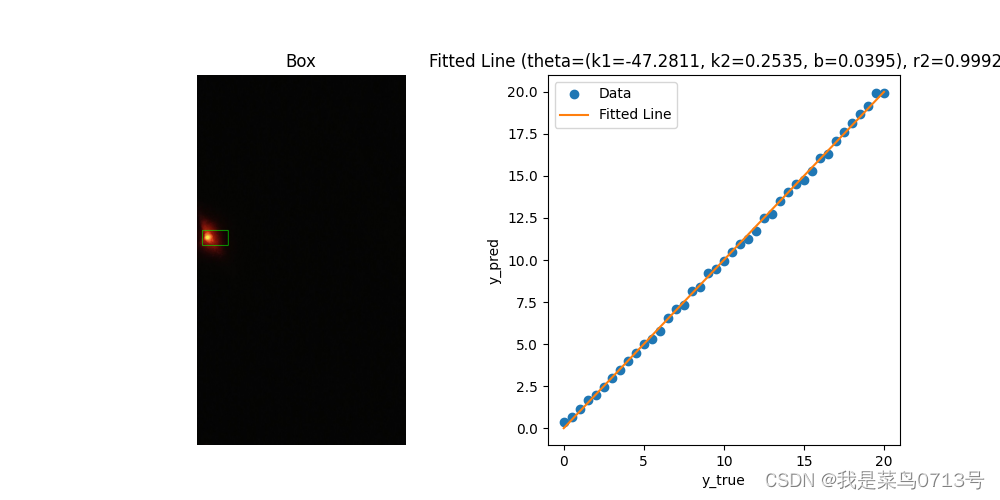
基于opencv的斜光测距及python实现
1.前言 最近做了一个基于opencv的斜光测距的小项目,东西不多,但是很有意思,值得拿出来学一学。项目里面需要比较精确的定位功能,将前人matlab代码移植到python上,并且做了一些优化,简化逻辑(毕竟我是专业的…...

梯度下降算法
占楼,明天写...

第5章:软件工程
第5章:软件工程 软件工程概述 软件生命周期 软件过程 1.能力成熟度模型(CMM) CMM(能力成熟度模型)是一个评估和确定组织软件过程成熟度的模型。它最早于1987年由美国国防部软件工程研究所(SEI)提出,其目的…...
含源代码)
cefsharp在splitContainer.Panel2中显示调试工具DevTools(非弹出式)含源代码
一、弹出式调试工具 (ShowDevTools) ChromiumWebBrowser webbrowser; public void showDevTools(){//定位到某元素webbrowser.ShowDevTools(null, parameters.XCoord, parameters.YCoord);...
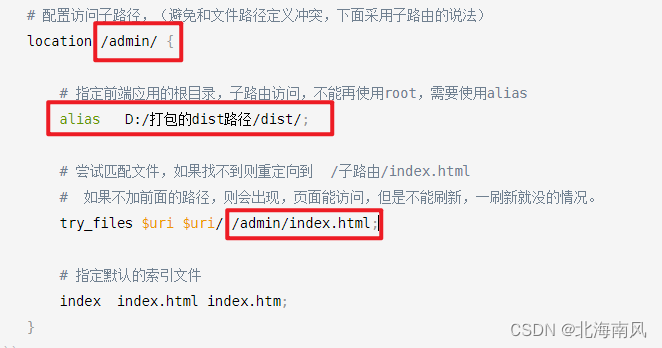
nginx部署多个项目;vue打包项目部署设置子路径访问;一个根域名(端口)配置多个子项目
本文解决: vue打包项目部署设置子路径访问;nginx部署多个子项目;一个ip/域名 端口 配置多个子项目;配置后,项目能访问,但是刷新页面就丢失的问题 注:本文需要nginx配置基础。基础不牢的可见文…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...
