SpringBoot 启动流程一
SpringBoot启动流程一
我们首先创建一个新的springboot工程
我们不添加任何依赖
查看一下pom文件

我们创建一个文本文档
记录我们的工作流程

我们需要的是通过打断点实现
我们首先看一下启动响应类

package com.bigdata1421.start_up;import org.springframework.boot.SpringApplication;
import org.springframework.boot.autoconfigure.SpringBootApplication;@SpringBootApplication
public class StartUpApplication {public static void main(String[] args) {SpringApplication.run(StartUpApplication.class, args);}}我们在这里启动
加载main方法
调用第10行的方法

这个run方法是干嘛的呢
我们进入源码查看

primarySource是指这个类
如果一个接口有四个实现类
但是你想设置某一个实现类为主体加载的
你就可以加上@Primary注解
这样这个实现类就是在自动转配中被加载的bean

我们再进入SpringApplication类里面run方法
中的run方法
是另一个run方法
我们再进入这个方法查看

我们在文本文档里记录一下
运行的是SpringApplication里面822行的这个方法

但是我们发现我们还是调用这个类里面的方法

再记录一下
我们在文本文档里再记录一下

StartUpApplication[10] -> SpringApplication.run(StartUpApplication.class, args);SpringApplication[822] -> return run(new Class[]{primarySource}, args);SpringApplication[826] -> return (new SpringApplication(primarySources)).run(args);这就是一个纯调用
去new了一个SpringApplication对象 让这个对象去调用run方法
参数为args这个数组
这个参数为命令行参数
我们可以在项目配置里面编辑这个参数

然而这个我们可以分成两部分
创建一个新的对象 用这个新的对象去调用方法

StartUpApplication[10] -> SpringApplication.run(StartUpApplication.class, args);SpringApplication[822] -> return run(new Class[]{primarySource}, args);SpringApplication[826] -> return (new SpringApplication(primarySources)).run(args);# 加载各种配置信息 初始化各种配置对象SpringApplication(primarySources)# 初始化容器new SpringApplication(primarySources).run(args)我们的核心就是这两块的内容
加载各种配置信息 初始化各种配置对象
初始化容器
个人号推广
博客主页
朱道阳-CSDN博客
Web后端开发
https://blog.csdn.net/qq_30500575/category_12624592.html?spm=1001.2014.3001.5482
Web前端开发
https://blog.csdn.net/qq_30500575/category_12642989.html?spm=1001.2014.3001.5482
数据库开发
https://blog.csdn.net/qq_30500575/category_12651993.html?spm=1001.2014.3001.5482
项目实战
https://blog.csdn.net/qq_30500575/category_12699801.html?spm=1001.2014.3001.5482
算法与数据结构
https://blog.csdn.net/qq_30500575/category_12630954.html?spm=1001.2014.3001.5482
计算机基础
https://blog.csdn.net/qq_30500575/category_12701605.html?spm=1001.2014.3001.5482
回忆录
https://blog.csdn.net/qq_30500575/category_12620276.html?spm=1001.2014.3001.5482
相关文章:

SpringBoot 启动流程一
SpringBoot启动流程一 我们首先创建一个新的springboot工程 我们不添加任何依赖 查看一下pom文件 我们创建一个文本文档 记录我们的工作流程 我们需要的是通过打断点实现 我们首先看一下启动响应类 package com.bigdata1421.start_up;import org.springframework.boot.Spr…...
打印机删除副本以后无法安装打印机驱动
根据知乎文章解决打印机驱动副本存在多个,打印机驱动无法删除,或者驱动包无法删除等问题。的方法删除打印机副本以后发现无论如何也装不上驱动了。 要么驱动安装成功,但是设备仍然是指定状态。 后面发现是删错文件夹了,教程里让删…...

Vue3中为Ant Design Vue中Modal.confirm自定义内容
在一次业务开发时代码时,碰到了一种既想要Modal.confirm样式,又想要定制其content内容的情况。 大部分情况下,使用Modal.method()这种方式时,可能content内容固定都是字符串,那如果想要做更高级的交互怎么办ÿ…...

智能猫砂盆到底哪家好用?自费实测聚宠、糯雪、CEWEY真实反馈!
快到夏天了,是不是还有人因为没挑选到喜欢的智能猫砂盆而苦恼着?太便宜怕不好用,太贵怕质量比不上价格。来来去去拖到现在还没决定,我作为养了四年猫的资深铲屎官,今天就来给大家传授经验,关于我是怎么从好…...

初阶数据结构之二叉树
那么本篇文是初阶数据结构这个系列的最后一篇文章,那么闲话少叙,我们直接进入正题 在讲二叉树的一些之前知识点之前,我先给大家送个小礼物哈 手搓二叉树 typedef int BTDataType ; typedef struct BinaryTreeNode { BTDataType _data …...

代码随想三刷动态规划篇8
代码随想三刷动态规划篇8 122. 买卖股票的最佳时机 II题目代码 123. 买卖股票的最佳时机 III题目代码 188. 买卖股票的最佳时机 IV题目代码 309. 买卖股票的最佳时机含冷冻期题目代码 122. 买卖股票的最佳时机 II 题目 链接 代码 class Solution {public int maxProfit(int…...

服务拆分的原则
目录 一、单一职责原则 二、服务自治原则 三、单向依赖 一、单一职责原则 单⼀职责原则原本是面向对象设计中的⼀个基本原则, 它指的是⼀个类应该专注于单⼀功能. 不要存在多于⼀个导致类变更的原因 在微服务架构中, ⼀个微服务也应该只负责⼀个功能或业务领域, 每个服务应该…...
离线安装docker社区版
提示:以下所有命令都在Ubuntu-24.04-live-server-amd64系统中运行 文章目录 前言一、离线包制作二、在目标系统上离线安装Docker CE总结 前言 安全原因,内部机器不能联网,要给新机器安装 docker-ce 只能使用离线安装方法。如果使用本文的下载…...

徒手绘制 Android 通用进度条
拖动条(FlexSeekBar),在Android的各个地方都非常常用,本文旨在自研一套通用的进度条,非常适合车载App使用 样式如下: 使用示例 <!--默认用法--> <com.max.android.ui.seekbar.FlexSeekBarandroi…...
【TB作品】矩阵键盘电话拨号,ATMEGA16单片机,Proteus仿真 atmega16矩阵键盘电话拨号
atmega16矩阵键盘电话拨号 c代码和仿真图: 使用ATmega16实现矩阵键盘电话拨号功能 项目背景 在电子设计和嵌入式系统开发中,矩阵键盘是常见的人机交互方式。它可以实现较多按键的输入,同时节省单片机的I/O资源。结合LCD显示和蜂鸣器&am…...

JavaScript(6)——数据类型转换
为什么需要类型转换? JavaScript是弱数据类型:JavaScript不知道变量到底属于哪种数据类型,只有赋值了才清除 使用表单,prompt获取的数据默认为字符串类型,此时不能直接进行算数运算 隐式转换 某些运算符被执行时&am…...

概率论与数理统计_下_科学出版社
contents 前言第5章 大数定律与中心极限定理独立同分布中心极限定理 第6章 数理统计的基本概念6.1 总体与样本6.2 经验分布与频率直方图6.3 统计量6.4 正态总体抽样分布定理6.4.1 卡方分布、t 分布、F 分布6.4.2 正态总体抽样分布基本定理 第7章 参数估计7.1 点估计7.1.1 矩估计…...

Android 复习layer-list使用
<shape android:shape"rectangle"> <size android:width"1dp" android:height"100px" /> <solid android:color"#FFFFFF" /> </shape> 通过shape画线段,通过 <item android:gravity"left|top"…...

汉光联创HGLM2200N黑白激光多功能一体机加粉及常见问题处理
基本参数: 机器型号:HGLM2200N 产品名称:A4黑白激光多功能一体机 基础功能:打印、扫描、复印 打印速度:22页/分钟 纸张输入容量:150-249页 单面支持纸张尺寸:A4、A5、A6 产品尺寸&#x…...

引领汽车软件开发走向ASPICE认证之路
亚远景科技与ASPICE认证的关系可以从以下几个方面来阐述: (要明确的是:在ASPICE行业中专业来说,ASPICE项目是没有认证,而只有评估。不过,为了方便沟通,人们常将这一评估过程称为认证。) 行业专…...

【C/C++ new/delete和malloc/free的异同及原理】
new/delete和malloc/free都是用于在C(以及C语言在malloc/free的情况下)中动态申请和释放内存的机制,但它们之间存在一些显著的异同点。以下是对这两组函数/运算符的异同点的详细分析: 相同点 目的相同:两者都用于在堆…...

Maven Archetype 自定义项目模板:高效开发的最佳实践
文章目录 前言一、Maven Archetype二、创建自定义 Maven Archetype三、定制 Archetype 模板四、手动创建 Archetype 模板项目五、FAQ5.1 如何删除自定义的模板5.2 是否可以在模板中使用空文件夹 六、小结推荐阅读 前言 在软件开发中,标准化和快速初始化项目结构能够…...

vue的ESLint 4格缩进 笔记
https://chatgpt.com/share/738c8560-5271-45c4-9de0-511fad862109 一,代码4格缩进设置 .eslintrc.js文件 module.exports { "rules": { "indent": ["error", 4] } }; 自动修复命令 npx eslint --fix "src/**/*.{…...
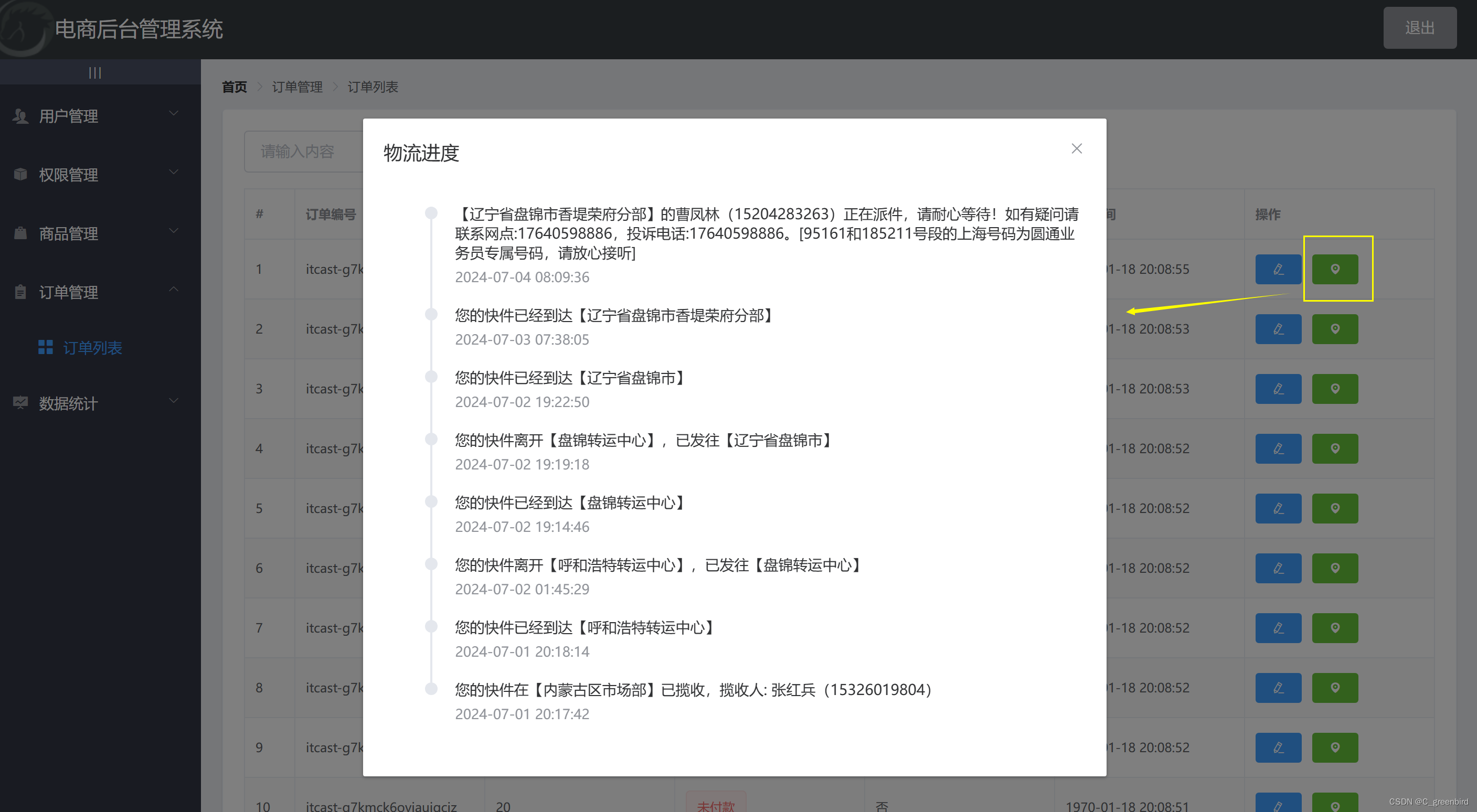
【前端项目笔记】8 订单管理
订单管理 效果展示: 在开发功能之前先创建分支order cls 清屏 git branch 查看所有分支(*代表当前分支) git checkout -b order 新建分支order git push -u origin order 将本地的当前分支提交到云端仓库origin中命名为order 通过路由方式…...

构建Yarn依赖树:深入解析与实践指南
构建Yarn依赖树:深入解析与实践指南 在现代JavaScript开发中,依赖管理是项目成功的关键。Yarn,作为Node.js生态系统中一个强大的包管理器,以其快速、可靠和安全的特性而闻名。本文将深入探讨Yarn如何构建依赖树,并提供…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...
