二叉搜索树原理及底层实现
二叉搜索树BST
概念
二叉搜索树又称二叉排序树,它可以是一棵空树,或者是具有以下性质的二叉树:若它的左子树不为空,则左子树上所有节点的值都小于根节点的值;若它的右子树不为空,则右子树上所有节点的值都大于根节点的值;它的左右子树也分别为二叉搜索树。
即当我们按中序来遍历输出这棵树的节点时,是有序的,按从小到大的顺序。
实现的细节
搜索key的过程Find/FindR
a.从根开始查找,val比根节点值大则往右边走查找,比根节点值小则往左边走查找;
b.最多查找高度次,走到到空,还没找到,说明这个值不存在。
//普通版本--用循环解决
bool Find(const K& key)
{Node* cur = _root;while (cur){if (cur->_key < key){cur = cur->_right;}else if (cur->_key > key){cur = cur->_left;}else{return true;}}return false;
}//用递归来解决
public:
bool FindR(const K& key)
{return _FindR(_root, key);
}
private:
bool _FindR(Node* root, const K& key)
{if (root == nullptr)return false;if (key > root->_key)return _FindR(root->_right, key);else if (key < root->_key)return _FindR(root->_left, key);elsereturn true;
}
插入key的过程Insert/InsertR
需要考虑以下场景:
a.树为空,则直接新增节点new,赋值给root指针;
b.树不为空,按二叉搜索树性质查找插入位置,即与根节点比较,比根节点的值小,往左查找;比根节点的值大,往右查找,找到该位置后插入新节点。这个过程需要用到2个指针,一个为判断当前值与key孰大孰小的cur指针,一个是保存cur的父节点的parent指针,最终要把key值节点插入在parent的左/右节点。【注意:此处的二叉搜索树无相同值】
bool Insert(const K& key)
{//如果根节点为空,直接插入这个值if (_root == nullptr){_root = new Node(key);return true;}Node* cur = _root;Node* parent = nullptr;while (cur){if (cur->_key == key){//如果二叉搜索树中已经有一样的值了,插入失败return false;}else if (key > cur->_key){parent = cur;//与根节点比较,比根节点的值小,往左走;比根节点的值大,往右走cur = cur->_right;}else{parent = cur;cur = cur->_left;}}cur = new Node(key);//与根节点比较,比根节点的值大,就链接在右边if (key > parent->_key){parent->_right = cur;}else{parent->_left = cur;}return true;
}public:bool InsertR(const K& key){return _InsertR(_root, key);}
private:
bool _InsertR(Node*& root, const K& key){//方式1 bool _InsertR(Node* root, const K& key)//if (key > root->_key)//{// if (root->_right == nullptr)// {// root->_right = new Node(key);// return true;// }// else// return _InsertR(root->_right, key);//}//else if (key < root->_key)//{// if (root->_left == nullptr)// {// root->_left = new Node(key);// return true;// }// else// return _InsertR(root->_left, key);//}//else// return false;//方式2 bool _InsertR(Node*& root, const K& key)if (root == nullptr){root = new Node(key);return true;}if (key > root->_key)return _InsertR(root->_right, key);else if (key < root->_key)return _InsertR(root->_left, key);elsereturn false;}
这里的二叉搜索树无法保证左右平衡。
删除的过程Erase/EraseR
首先查找元素是否在二叉搜索树中,如果不存在,则返回, 否则要删除的结点可能分下面四种情况:
- 要删除的结点无孩子结点–直接删除,其父节点原来指向它的变成指向空
- 要删除的结点只有左孩子结点–托孤,让该节点的父节点直接指向该节点的孩子节点
- 要删除的结点只有右孩子结点–托孤,让该节点的父节点直接指向该节点的孩子节点
- 要删除的结点有左、右孩子结点–替换,找左子树的最大和右子树的最小
看起来待删除节点的处理方式有4种情况,实际上情况1可以与情况2或者3合并起来,因此真正的删除过程如下:
- 删除该结点且使被删除节点的父结点指向被删除节点的左孩子结点–直接删除
- 删除该结点且使被删除节点的父结点指向被删除结点的右孩子结点–直接删除
- 在它的右子树中寻找中序下的第一个结点(关键码最小),用它的值填补到被删除节点中,再来处理该结点的删除问题–替换法删除
//普通版本
bool Erase(const K& key)
{Node* parent = nullptr;Node* cur = _root;while (cur){//与根节点比较,比根节点的值大,往右走;比根节点的值小,往左走if (key > cur->_key){parent = cur;cur = cur->_right;}else if (key < cur->_key){parent = cur;cur = cur->_left;}else{//能走到这,就说明找到了要删除的这个节点,要删除的节点为cur//情况1:左子节点为空,右子节点不为空if (cur->_left == nullptr){//需要特殊处理根节点,因为根节点无父节点if (cur == _root){_root = cur->_right;}else{//cur为parent的左子节点,cur的子节点就得继承parent的左子节点if (parent->_left == cur){parent->_left = cur->_right;}//cur为parent的右子节点,cur的子节点就得继承parent的右子节点else{parent->_right = cur->_right;}}delete cur;}//情况2:左子节点不为空,右子节点为空else if (cur->_right == nullptr){//需要特殊处理根节点,因为根节点无父节点if (cur == _root){_root = cur->_left;}else{//cur为parent的左子节点,cur的子节点就得继承parent的左子节点if (parent->_left == cur){parent->_left = cur->_left;}//cur为parent的右子节点,cur的子节点就得继承parent的右子节点else{parent->_right = cur->_left;}}delete cur;}//情况3:左右子节点均不为空else{//在cur的右子树中寻找中序的第一个结点Node* parent = cur;Node* minRight = cur->_right;//此处前置条件是cur的左右子树均不为空while (minRight->_left){parent = minRight;minRight = minRight->_left;}//交换cur和minRight的值cur->_key = minRight->_key;//删除minRightif (minRight == parent->_left)parent->_left = minRight->_right;elseparent->_right = minRight->_right;delete minRight;}return true;}}//走到这,说明没找到return false;
}//递归版本
public:bool EraseR(const K& key){return _EraseR(_root, key);}
private:bool _EraseR(Node*& root, const K& key){if (root == nullptr)return false;if (key > root->_key){return _EraseR(root->_right, key);}else if (key < root->_key){return _EraseR(root->_left, key);}else{Node* del = root;//相等就开始删除if (root->_left == nullptr){root = root->_right;}//情况2:左子节点不为空,右子节点为空else if (root->_right == nullptr){ root = root->_left;}//情况3:左右子节点均不为空else{Node* minRight = root->_right;while (minRight->left){minRight = minRight->left;}swap(root->_key, minRight->_key);// 转换成在子树中去删除节点return _EraseR(root->_right, key);}delete del;return true; }}
中序遍历InOrder
在不暴露根节点_root的情况下(比如写一个函数getroot()等让用户获取),套一层函数接口就直接在类内使用这个_root,实现中序遍历
void InOrder()
{_InOrder(_root);std::cout << std::endl;
}
private:
void _InOrder(Node* root)
{//中序:左根右if (root == nullptr) return;_InOrder(root->_left);std::cout << root->_key << " ";_InOrder(root->_right);
}
注意:二叉搜素树不支持改,对于二叉搜索树而言,仅仅修改对应节点的值,极有可能破坏原结构,所以改=删除+插入
构造函数、拷贝构造函数、赋值构造函数、析构函数
public:BSTree():_root(nullptr){}BSTree(const BSTree<K>& t){_root = Copy(t._root);}BSTree<K>& operator=(BSTree<K> t){swap(_root, t._root);return *this;}~BSTree(){Destory(_root);_root = nullptr;}
private:void Destory(Node* root){if (root == nullptr)return;//按后序来删除Destory(root->_left);Destory(root->_right);delete root;}Node* Copy(Node* root){if (root == nullptr)return nullptr;//前序遍历,再递归拷贝Node* newnode = new Node(root->_key);newnode->_left = Copy(root->_left);newnode->_right = Copy(root->_right);return newnode;}
应用场景
K模型–判断某个key在不在的场景;KV模型–通过key查找或修改value
- K模型:K模型即只有key作为关键码,结构中只需要存储Key即可,关键码即为需要搜索到的值。
比如:给一个单词word,判断该单词是否拼写正确,具体方式如下:以词库中所有单词集合中的每个单词作为key,构建一棵二叉搜索树在二叉搜索树中检索该单词是否存在,存在则拼写正确,不存在则拼写错误。其他场景:检查单词拼写是否正确/车库出入系统/宿舍楼门禁系统
- KV模型:每一个关键码key,都有与之对应的值Value,即
<Key, Value>的键值对。该种方式在现实生活中非常常见:
比如英汉词典就是英文与中文的对应关系,通过英文可以快速找到与其对应的中文,英文单词与其对应的中文<word, chinese>就构成一种键值对;再比如统计单词次数,统计成功后,给定单词就可快速找到其出现的次数,单词与其出现次数就是<word, count>就构成一种键值对。其他场景:英汉互译/学号学生对应
性能分析
插入和删除操作都必须先查找,查找效率代表了二叉搜索树中各个操作的性能。
对有n个结点的二叉搜索树,若每个元素查找的概率相等,则二叉搜索树平均查找长度是结点在二叉搜索树的深度的函数,即结点越深,则比较次数越多。
但对于同一个关键码集合,如果各关键码插入的次序不同,可能得到不同结构的二叉搜索树:
- 最优情况下,二叉搜索树为完全二叉树(或者接近完全二叉树),其平均比较次数为:log2Nlog_2 Nlog2N
- 最差情况下,二叉搜索树退化为单支树(或者类似单支),其平均比较次数为:N2\frac{N}{2}2N
但是如果退化成单支树,二叉搜索树的性能就很差,后续引入红黑树和AVL树来解决。
相关文章:

二叉搜索树原理及底层实现
二叉搜索树BST 概念 二叉搜索树又称二叉排序树,它可以是一棵空树,或者是具有以下性质的二叉树:若它的左子树不为空,则左子树上所有节点的值都小于根节点的值;若它的右子树不为空,则右子树上所有节点的值都…...

python自动化办公(一)
本文代码参考其他教程书籍实现。 文章目录文件读写open函数读取文本文件写入文本文件文件和目录操作使用os库使用shutil库文件读写 open函数 open函数有8个参数,常用前4个,除了file参数外,其他参数都有默认值。file指定了要打开的文件名称&a…...
LeetCode - 198 打家劫舍
目录 题目来源 题目描述 示例 提示 题目解析 算法源码 题目来源 198. 打家劫舍 - 力扣(LeetCode) 题目描述 你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装…...
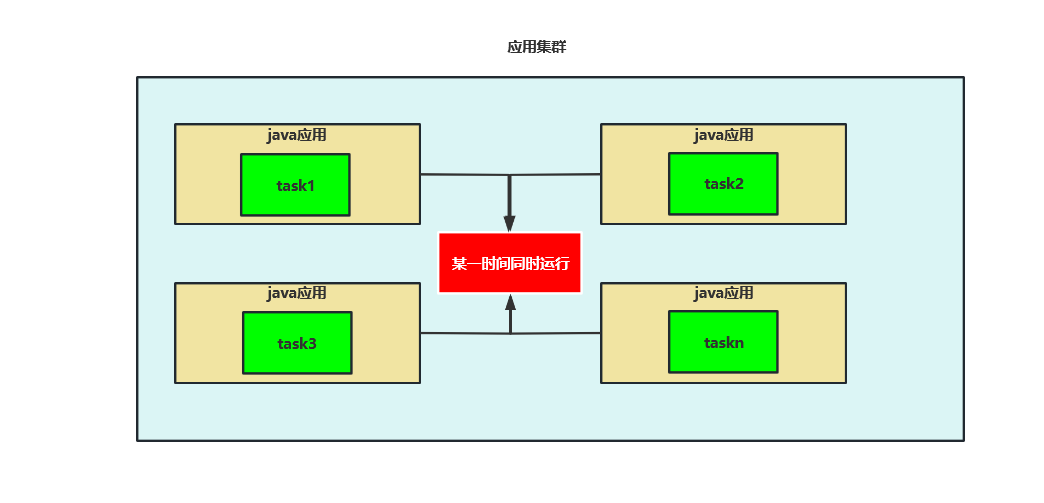
简单粗暴的分布式定时任务解决方案
分布式定时任务1.为什么需要定时任务?2.数据库实现分布式定时任务3.基于redis实现1.为什么需要定时任务? 因为有时候我们需要定时的执行一些操作,比如业务中产生的一些临时文件,临时文件不能立即删除,因为不清楚用户是…...

蓝桥杯第五天刷题
第一题:数的分解题目描述本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。把 2019 分解成 3 个各不相同的正整数之和,并且要求每个正整数都不包含数字 2和 4,一共有多少种不同的分解方法&…...
Java数组的定义和使用(万字详解)
目录 编辑 一. 数组的基本概念 1、什么是数组 2、数组的创建及初始化 1、数组的创建 2、数组的初始化 3、数组的使用 (1)数组中元素访问 (3)遍历数组 二、数组是引用类型 1、初始JVM的内存分布 2、基本类型变量与引用类…...

【SpringBoot】自定义Starter
🚩本文已收录至专栏:Spring家族学习之旅 👍希望您能有所收获 一.概述 在使用SpringBoot进行开发的时候,我们发现使用很多技术都是直接导入对应的starter,然后就实现了springboot整合对应技术,再加上一些简…...
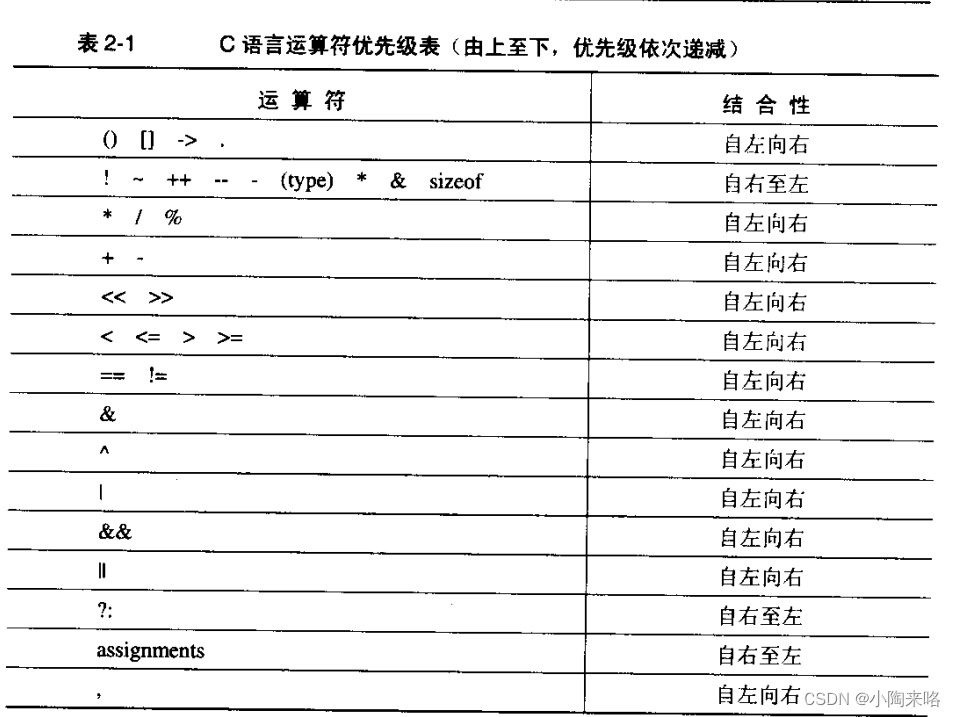
【C陷阱与缺陷】----语法陷阱
💯💯💯 要理解一个C程序,必须理解这些程序是如何组成声明,表达式,语句的。虽然现在对C的语法定义很完善,几乎无懈可击,大门有时这些定义与人们的直觉相悖,或容易引起混淆…...

虹科分享| 关于TrueNAS十问十答
上一篇文章我们向您介绍了虹科新品HK-TrueNAS企业存储,很多小伙伴会疑问到底什么是NAS存储,之前常用的磁盘、磁带属于什么存储架构,NAS存储好在哪里,什么时候使用NAS?今天我们整理了关于TrueNAS的十问十答,…...
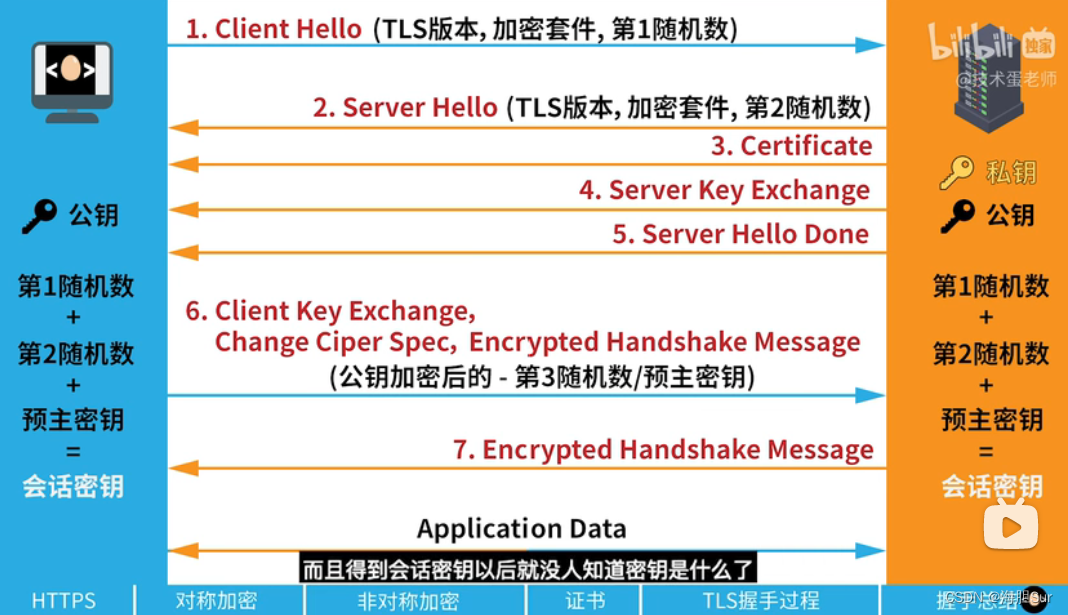
Https 笔记
HTTP TLS TLS 的前身是 SSL 非对称加密的核心: 两个密钥(公私) https 需要第三方CA(证书授权中心)申请SSL证书以确定其真实性 证书种包含了特定的公钥和私钥 密钥交换 自己将私钥上锁后发给对方对方也上锁 在还回来…...

【Python+requests+unittest+excel】实现接口自动化测试框架
一、框架结构: 工程目录 二、Case文件设计 三、基础包 base 3.1 封装get/post请求(runmethon.py) 1 import requests2 import json3 class RunMethod:4 def post_main(self,url,data,headerNone):5 res None6 if heade…...
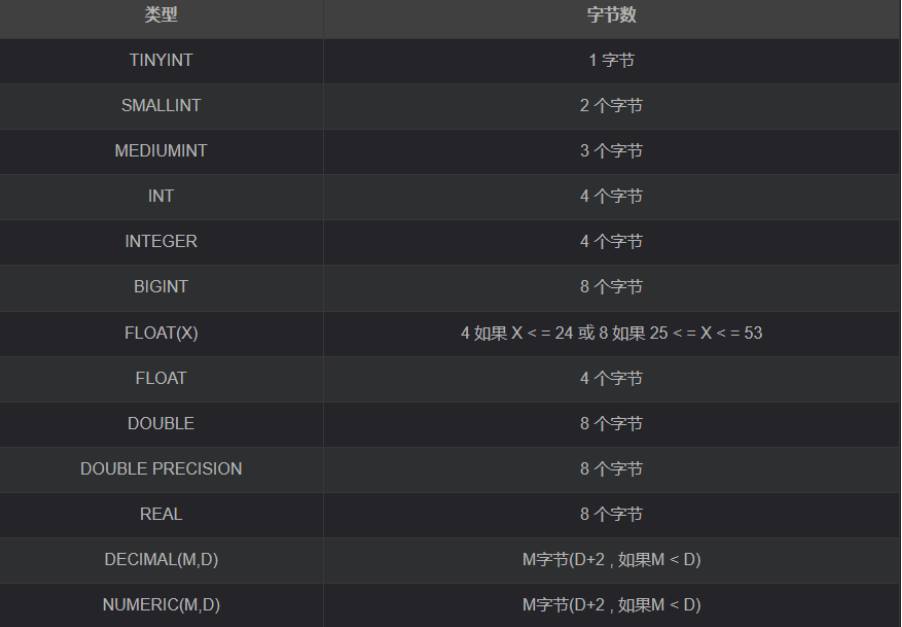
MySQL终端的使用及其数据类型的使用
什么是数据库?数据库(Database)是按照数据结构来组织、存储和管理数据的仓库。每个数据库都有一个或多个不同的 API 用于创建,访问,管理,搜索和复制所保存的数据。我们也可以将数据存储在文件中,…...
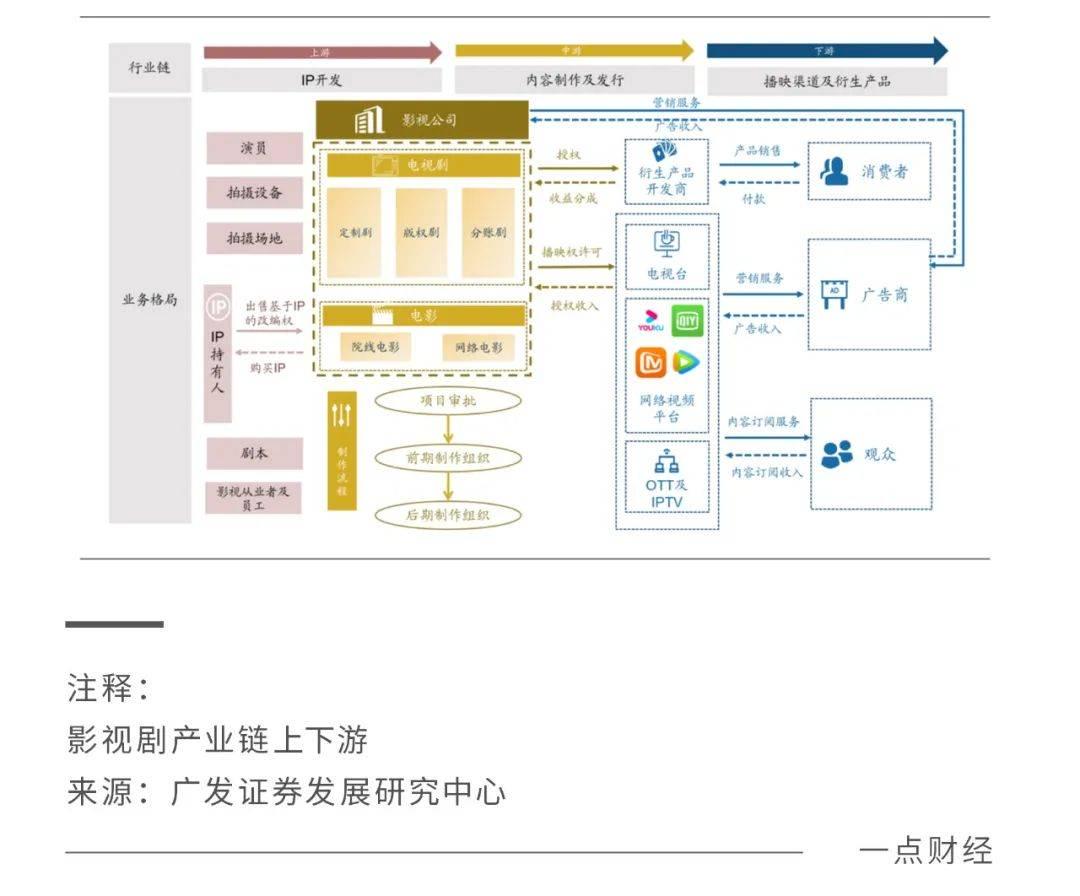
长视频终局:一场考验资金储备的消耗战
赢者通吃,似乎已成为各行各业的常识,但事实真的是这样吗?20世纪70年代,石油价格高涨,在墨西哥湾油田拍卖中高价拍得油田的企业,要么亏损,要么收入低于预期,但仍然有无数企业在高价竞…...

javaEE初阶 — CSS 常用的属性
文章目录CSS 常用的属性1 字体属性1.1 设置字体家族 font-family1.2 设置字体大小 font-size1.3 设置字体粗细 font-weight1.4 文字倾斜 font-style2 文本属性2.1 文本颜色2.2 文本对齐2.3 文本装饰2.4 文本缩进2.5 行高3 背景属性3.1 背景颜色3.2 背景图片3.3 背景位置3.4 背景…...

【面试题】如何取消 script 标签发出的请求
大厂面试题分享 面试题库前后端面试题库 (面试必备) 推荐:★★★★★地址:前端面试题库问题之前在业务上有这样一个场景,通过 script 标签动态引入了一个外部资源,具体方式是这样的const script document.…...
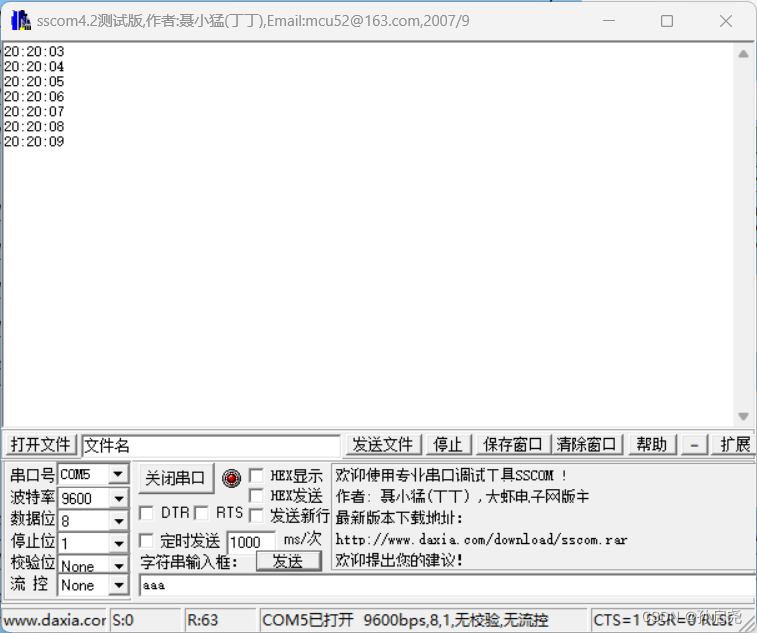
蓝桥杯嵌入式(G4系列):RTC时钟
前言: 关于RTC时钟的HAL库配置我也是第一次,之前都是用库函数的写法,这里写下这篇博客来记录一下自己的学习过程。 STM32Cubemx配置: 首先点击左侧的Timers的RTC,勾选以下选项 进入时钟树配置 进入时间设置࿰…...
Linux——进程间通信1
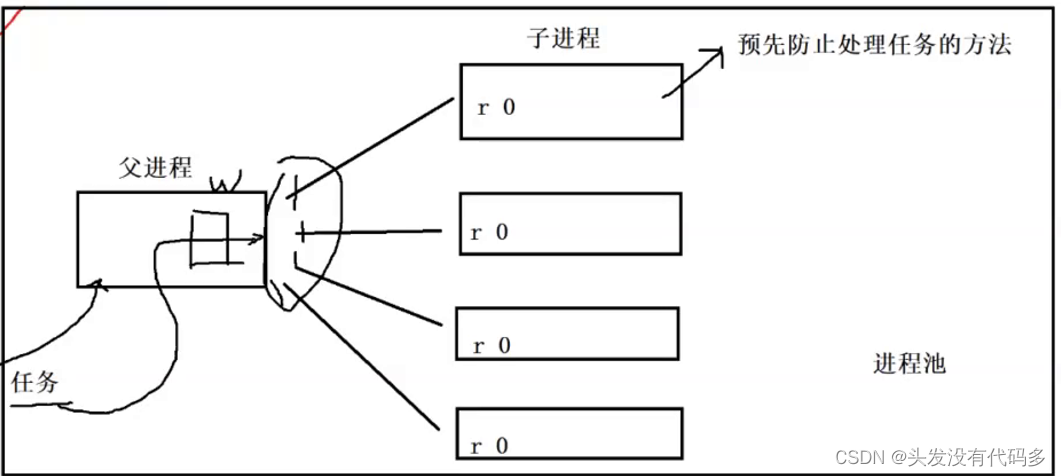
目录 进程间通信目的 进程间通信标准 管道 匿名管道 管道实现进程间通信 管道的特点 进程池 ProcessPool.cc Task.hpp 习题 进程间通信目的 数据传输:一个进程需要将它的数据发送给另一个进程 资源共享:多个进程之间共享同样的资源。 通知事件…...

循环语句——“Python”
各位CSDN的uu们你们好呀,今天小雅兰的内容是Python中的循环语句呀,分为while循环和for循环,下面,让我们进入循环语句的世界吧 循环语句 while循环 for循环 continue和break 循环语句小结 人生重开模拟器 设置初始属性 设置性别…...

Python synonyms查找中文任意词汇的同义词近义词
Python synonyms查找中文任意词汇的同义词近义词 作者:虚坏叔叔 博客:https://xuhss.com 早餐店不会开到晚上,想吃的人早就来了!😄 一、安装 对于非专业的开发人员来说可以简单的使用Python一行代码来找到同义词。这…...

三分钟了解http和https
对应测试人员都会听过http请求和响应.在这里给大家介绍http相关的知识 一.http和https基本概念 HTTP:是互联网上应用最为广泛的一种网络协议,是一个客户端和服务器端请求和应答的标准(TCP),用于从WWW服务器传输超文本…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

Windows安装Miniconda
一、下载 https://www.anaconda.com/download/success 二、安装 三、配置镜像源 Anaconda/Miniconda pip 配置清华镜像源_anaconda配置清华源-CSDN博客 四、常用操作命令 Anaconda/Miniconda 基本操作命令_miniconda创建环境命令-CSDN博客...

根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的----NTFS源代码分析--重要
根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的 第一部分: 0: kd> g Breakpoint 9 hit Ntfs!ReadIndexBuffer: f7173886 55 push ebp 0: kd> kc # 00 Ntfs!ReadIndexBuffer 01 Ntfs!FindFirstIndexEntry 02 Ntfs!NtfsUpda…...

Golang——7、包与接口详解
包与接口详解 1、Golang包详解1.1、Golang中包的定义和介绍1.2、Golang包管理工具go mod1.3、Golang中自定义包1.4、Golang中使用第三包1.5、init函数 2、接口详解2.1、接口的定义2.2、空接口2.3、类型断言2.4、结构体值接收者和指针接收者实现接口的区别2.5、一个结构体实现多…...
