揭秘数据之美:【Seaborn】在现代【数学建模】中的革命性应用
目录
已知数据集 tips
生成数据集并保存为CSV文件
数据预览:
导入和预览数据
步骤1:绘制散点图(Scatter Plot)
步骤2:添加回归线(Regression Analysis)
步骤3:分类变量分析(Categorical Variables)
步骤4:箱线图(Box Plot)
步骤5:小提琴图(Violin Plot)
步骤6:绘制热力图(Heatmap)
编辑
总结
1. 生成数据集并保存为CSV文件
2. 导入和预览数据
3. 绘制散点图(Scatter Plot)
4. 添加回归线(Regression Analysis)
5. 分类变量分析(Categorical Variables)
6. 绘制箱线图(Box Plot)
7. 绘制小提琴图(Violin Plot)
8. 绘制热力图(Heatmap)


专栏:数学建模学习笔记
python相关库的安装:pandas,numpy,matplotlib,statsmodels
总篇:【数学建模】—【新手小白到国奖选手】—【学习路线】
第一卷:Numpy
第二卷:Pandas
第三卷:Matplotlib
在数据科学和数学建模的过程中,数据可视化是非常重要的一环。通过可视化,我们能够更直观地理解数据的分布和关系,从而为后续的分析和建模打下坚实的基础。本篇文章将围绕一个具体的实例,详细讲解如何使用Seaborn库进行数据可视化。我们将使用Seaborn内置的数据集tips,该数据集包含了一些餐馆的小费数据。我们的目标是通过数据可视化,探索影响小费金额的因素,并尝试建立一个数学模型。
已知数据集 tips
tips 数据集包含以下几个主要字段:
total_bill: 总账单金额tip: 小费金额sex: 性别smoker: 是否吸烟day: 就餐日期time: 就餐时间(午餐或晚餐)size: 就餐人数
生成数据集并保存为CSV文件
import pandas as pd
import numpy as np# 设置随机种子
np.random.seed(0)# 生成数据
n = 1000
total_bill = np.round(np.random.uniform(5, 50, n), 2)
tip = np.round(total_bill * np.random.uniform(0.1, 0.3, n), 2)
sex = np.random.choice(['Male', 'Female'], n)
smoker = np.random.choice(['Yes', 'No'], n)
day = np.random.choice(['Thur', 'Fri', 'Sat', 'Sun'], n)
time = np.random.choice(['Lunch', 'Dinner'], n)
size = np.random.randint(1, 6, n)# 创建DataFrame
tips = pd.DataFrame({'total_bill': total_bill,'tip': tip,'sex': sex,'smoker': smoker,'day': day,'time': time,'size': size
})# 保存数据集到CSV文件
tips.to_csv('tips.csv', index=False)# 显示数据集的前几行
print(tips.head())
数据预览:
| total_bill | tip | sex | smoker | day | time | size |
|---|---|---|---|---|---|---|
| 29.70 | 6.49 | Female | No | Fri | Lunch | 5 |
| 37.18 | 3.79 | Female | Yes | Thur | Lunch | 2 |
| 32.12 | 6.27 | Female | No | Thur | Lunch | 4 |
| 29.52 | 7.14 | Female | No | Fri | Lunch | 5 |
| 24.06 | 2.62 | Female | Yes | Sun | Dinner | 5 |
导入和预览数据
在生成数据后,我们导入必要的可视化库,并预览数据。
import seaborn as sns
import matplotlib.pyplot as plt
import pandas as pd# 读取本地示例数据集
tips = pd.read_csv('tips.csv')# 显示数据集的前几行
print(tips.head())

详解:
导入必要的库:
seaborn: 用于数据可视化的主要库。matplotlib.pyplot: Seaborn是基于Matplotlib构建的,所以我们需要同时导入Matplotlib来进行图表的展示。读取数据:
- 使用
pandas.read_csv函数从CSV文件中读取数据。预览数据:
- 使用
print(tips.head())函数来显示数据集的前几行,帮助我们快速了解数据的结构和内容。
步骤1:绘制散点图(Scatter Plot)
我们首先绘制一个散点图,展示总账单(total_bill)与小费(tip)之间的关系。
# 绘制散点图
sns.scatterplot(data=tips, x='total_bill', y='tip')
plt.title('Scatter plot of Total Bill vs Tip')
plt.xlabel('Total Bill')
plt.ylabel('Tip')
plt.show()

绘制散点图:
- 使用
seaborn.scatterplot函数,其中data参数指定数据集,x和y参数分别指定横轴和纵轴的数据字段。设置图表标题和标签:
- 使用
plt.title设置图表标题。- 使用
plt.xlabel和plt.ylabel分别设置横轴和纵轴的标签。显示图表:
- 使用
plt.show()函数来显示图表。
散点图是一种常用的图表类型,用于展示两个变量之间的关系。在这个例子中,使用seaborn.scatterplot函数绘制总账单(total_bill)与小费(tip)之间的散点图。通过散点图,可以直观地看到总账单和小费之间的关系。从图中可以看出,小费随总账单的增加而增加,但这种关系是否是线性的还需要进一步分析。
步骤2:添加回归线(Regression Analysis)
为了更好地了解总账单和小费之间的关系,我们可以使用Seaborn的 lmplot 函数来添加一条回归线。
# 绘制带回归线的散点图
sns.lmplot(data=tips, x='total_bill', y='tip')
plt.title('Total Bill vs Tip with Regression Line')
plt.xlabel('Total Bill')
plt.ylabel('Tip')
plt.show()

绘制带回归线的散点图:
- 使用
seaborn.lmplot函数,其中data参数指定数据集,x和y参数分别指定横轴和纵轴的数据字段。lmplot函数不仅绘制散点图,还会自动添加一条回归线,用于展示两个变量之间的线性关系。设置图表标题和标签:
- 同样使用
plt.title、plt.xlabel和plt.ylabel设置图表的标题和轴标签。显示图表:
- 使用
plt.show()函数来显示图表。
回归分析是一种统计方法,用于研究两个变量之间的关系。在这个例子中,使用Seaborn的lmplot函数来绘制带有回归线的散点图。通过添加回归线,可以更清楚地看到总账单和小费之间的线性关系。这条回归线表示小费随总账单增加的趋势,图中还会显示回归线的置信区间。
步骤3:分类变量分析(Categorical Variables)
接下来,我们分析性别、吸烟情况等分类变量对小费的影响。
# 使用hue参数根据性别绘制不同颜色的散点图
sns.scatterplot(data=tips, x='total_bill', y='tip', hue='sex')
plt.title('Total Bill vs Tip by Gender')
plt.xlabel('Total Bill')
plt.ylabel('Tip')
plt.show()

根据分类变量绘制散点图:
- 使用
seaborn.scatterplot函数,通过hue参数指定分类变量(例如性别),从而根据不同类别绘制不同颜色的点。设置图表标题和标签:
- 使用
plt.title、plt.xlabel和plt.ylabel设置图表的标题和轴标签。显示图表:
- 使用
plt.show()函数来显示图表。
分类变量(如性别、吸烟情况等)在数据分析中非常重要,因为它们能够提供关于数据分布的更多信息。在这个例子中,使用seaborn.scatterplot函数,根据性别绘制不同颜色的散点图。通过这种方式,可以看到性别对总账单和小费关系的影响。例如,可以观察到男性和女性在小费上的差异。
步骤4:箱线图(Box Plot)
箱线图可以帮助我们了解数据的分布及其异常值。
# 绘制箱线图展示不同日期的总账单分布
sns.boxplot(data=tips, x='day', y='total_bill')
plt.title('Box plot of Total Bill by Day')
plt.xlabel('Day')
plt.ylabel('Total Bill')
plt.show()

绘制箱线图:
- 使用
seaborn.boxplot函数,其中data参数指定数据集,x和y参数分别指定分类变量和连续变量。- 箱线图可以展示数据的中位数、四分位数及其异常值。
设置图表标题和标签:
- 使用
plt.title、plt.xlabel和plt.ylabel设置图表的标题和轴标签。显示图表:
- 使用
plt.show()函数来显示图表。
箱线图是一种统计图表,用于展示数据分布的五个统计量:最小值、第一四分位数、中位数、第三四分位数和最大值。箱线图还可以展示异常值。在这个例子中,使用seaborn.boxplot函数绘制不同日期(day)的总账单(total_bill)分布。通过箱线图,可以看到不同日期的总账单分布情况,并识别出哪些数据点是异常值。例如,可以观察到在某些日期,总账单的分布范围较广,而在另一些日期,分布范围较窄。
步骤5:小提琴图(Violin Plot)
小提琴图结合了箱线图和核密度图,可以提供关于数据分布的更多信息。
# 绘制小提琴图展示不同日期的小费分布
sns.violinplot(data=tips, x='day', y='tip')
plt.title('Violin plot of Tip by Day')
plt.xlabel('Day')
plt.ylabel('Tip')
plt.show()

绘制小提琴图:
- 使用
seaborn.violinplot函数,其中data参数指定数据集,x和y参数分别指定分类变量和连续变量。- 小提琴图展示了数据分布的核密度估计,并结合了箱线图的元素。
设置图表标题和标签:
- 使用
plt.title、plt.xlabel和plt.ylabel设置图表的标题和轴标签。显示图表:
- 使用
plt.show()函数来显示图表。
小提琴图结合了箱线图和核密度图的优点,可以更详细地展示数据分布的特征。在这个例子中,使用seaborn.violinplot函数绘制不同日期(day)的小费(tip)分布。通过小提琴图,可以看到不同日期的小费分布情况,并识别出数据分布的密度和异常值。例如,可以观察到在某些日期,小费的分布较为集中,而在另一些日期,分布较为分散。
步骤6:绘制热力图(Heatmap)
热力图适合展示矩阵数据,比如相关矩阵。例如,绘制数据集的相关矩阵:
# 选择数值列
numeric_tips = tips.select_dtypes(include='number')# 计算相关矩阵并绘制热力图
corr = numeric_tips.corr()
plt.figure(figsize=(10, 8))
sns.heatmap(corr, annot=True, cmap='coolwarm', linewidths=0.5)
plt.title('Heatmap of Correlation Matrix')
plt.show()

计算相关矩阵:
- 使用
DataFrame.corr()函数计算数据集中数值变量之间的相关系数。绘制热力图:
- 使用
seaborn.heatmap函数绘制热力图。corr:相关矩阵,作为热力图的数据输入。annot=True:在每个单元格中显示相关系数的数值。cmap='coolwarm':设置热力图的颜色映射,coolwarm颜色映射使得正相关和负相关的数据点能够通过颜色区分开来。linewidths=0.5:设置每个单元格之间的间隔线宽度。设置图表大小:使用
plt.figure(figsize=(10, 8))设置图表的大小,确保图表清晰可读。设置图表标题:使用
plt.title设置图表的标题。显示图表:使用
plt.show()函数来显示热力图。
相关矩阵热力图解释:
- 对角线:热力图的对角线上的值都是1,因为每个变量与自身的相关系数都是1。
- 变量之间的相关性:热力图的非对角线单元格显示了不同变量之间的相关系数。颜色的深浅表示相关性强弱,颜色的方向(冷暖)表示正相关或负相关。
通过这些详细的步骤,我们能够全面地分析和可视化餐馆小费数据,深入了解影响小费的各种因素,为进一步的数学建模和决策提供有力的支持。
总结
1. 生成数据集并保存为CSV文件
首先,我们生成了一个包含餐馆小费信息的模拟数据集,并将其保存为CSV文件。数据集包含以下字段:total_bill、tip、sex、smoker、day、time和size。
2. 导入和预览数据
使用Pandas库读取本地CSV文件,并预览数据集的前几行,以了解数据的结构和内容。
3. 绘制散点图(Scatter Plot)
使用Seaborn的scatterplot函数绘制散点图,展示总账单(total_bill)与小费(tip)之间的关系。
4. 添加回归线(Regression Analysis)
使用Seaborn的lmplot函数在散点图上添加回归线,以更清晰地展示总账单和小费之间的线性关系。
5. 分类变量分析(Categorical Variables)
使用scatterplot函数的hue参数,根据性别绘制不同颜色的散点图,分析性别对总账单和小费关系的影响。
6. 绘制箱线图(Box Plot)
使用Seaborn的boxplot函数绘制箱线图,展示不同日期的总账单分布,帮助识别数据的中位数、四分位数及其异常值。
7. 绘制小提琴图(Violin Plot)
使用Seaborn的violinplot函数绘制小提琴图,结合箱线图和核密度图,提供更多关于数据分布的信息。
8. 绘制热力图(Heatmap)
计算数据集中数值变量之间的相关矩阵,使用Seaborn的heatmap函数绘制热力图,直观地展示各变量之间的相关性。
通过这些步骤,可以全面地分析和可视化餐馆小费数据,深入了解影响小费的各种因素,为进一步的数学建模和决策提供有力的支持。
相关文章:

揭秘数据之美:【Seaborn】在现代【数学建模】中的革命性应用
目录 已知数据集 tips 生成数据集并保存为CSV文件 数据预览: 导入和预览数据 步骤1:绘制散点图(Scatter Plot) 步骤2:添加回归线(Regression Analysis) 步骤3:分类变量分析&…...

【宠粉赠书】UML 2.5基础、建模与设计实践
为了回馈粉丝们的厚爱,今天小智给大家送上一套系统建模学习的必备书籍——《UML 2.5基础、建模与设计实践》。下面我会详细给大家介绍这本书,文末留有领取方式。 图书介绍 《UML 2.5基础、建模与设计实践》以实战为主旨,结合draw.io免费软件…...

Python中几个重要的集合
Python中几个重要的集合(Collection)类型,包括列表(List)、元组(Tuple)、集合(Set)和字典(Dictionary) 1. 列表(List) 说…...
【JS】纯web端使用ffmpeg实现的视频编辑器-视频合并
纯前端实现的视频合并 接上篇ffmpeg文章 【JS】纯web端使用ffmpeg实现的视频编辑器 这次主要添加了一个函数,实现了视频合并的操作。 static mergeArgs(timelineList) {const cmd []console.log(时间轴数据,timelineList)console.log("文件1",this.readD…...

解决Python用xpath爬取不到数据的一个思路
前言 最近在学习Python爬虫的知识,既然眼睛会了难免忍不住要实践一把。 不废话直接上主题 代码不复杂,简单的例子奉上: import requests from lxml import etreecookie 浏览器F12网络请求标头里有 user_agent 浏览器F12网络请求标头里有…...

C#面:如何把一个array复制到arrayist里
要将一个数组复制到ArrayList中,可以使用ArrayList的AddRange方法。以下是一个示例代码: int[] array { 1, 2, 3, 4, 5 }; ArrayList arrayList new ArrayList(); arrayList.AddRange(array); 在上面的代码中,我们首先创建了一个整数类型…...

解决前后端同一个端口跨域问题
前端起了一个代理 如果url是api开头的自动代理访问8080端口(解决前后端端口不一致要么是前端代理,要么是后端加过滤器) proxy:{/api:{target:http://localhost:8080,changeOrigin : true,// 替换去掉路径上的api// rewrite:(path)>path.r…...

《C语言》认识数据类型和理解变量
🌹个人主页🌹:喜欢草莓熊的bear 🌹专栏🌹:C语言基础 目录 前言 一、数据类型的介绍 1.1 字符型 1.2 整形 1.3 浮点型 1.4 布尔类型 1.5 各种数据类型的长度 1.5.1 sizeof操作符 1.5.2 数据类型长度…...

【ARM 常见汇编指令学习 7.1 -- LDRH 半字读取指令】
请阅读【嵌入式开发学习必备专栏】 文章目录 LDRH 使用介绍LDRH(Load Register Half-word)总结 LDRH 使用介绍 在ARMv9架构中,汇编指令LDRH用于从内存中载入数据到寄存器的指令,下面将分别对它进行详细介绍: LDRH&am…...

C++期末整理
课堂笔记 构造与析构 #include <iosteam> #include <cstring> using namespace std;struct Date {int y, m, d;void setDate(int, int, int);Date(int yy, int mm, int dd) {y yy, m mm, d dd;} };class Student { private:char* name;Date birthday; public:…...

技术派Spring事件监听机制及原理
Spring事件监听机制是Spring框架中的一种重要技术,允许组件之间进行松耦合通信。通过使用事件监听机制,应用程序的各个组件可以在其他组件不直接引用的情况下,相互发送和接受消息。 需求 在技术派中有这样一个需求,当发布文章或…...

秋招突击——设计模式补充——简单工厂模式和策略模式
文章目录 引言正文简单工厂模式策略模式策略模式和工厂模式的结合策略模式解析 总结 引言 一个一个来吧,面试腾讯的时候,问了我单例模式相关的东西,自己这方面的东西,还没有看过。这里需要需要补充一下。但是设计模式有很多&…...
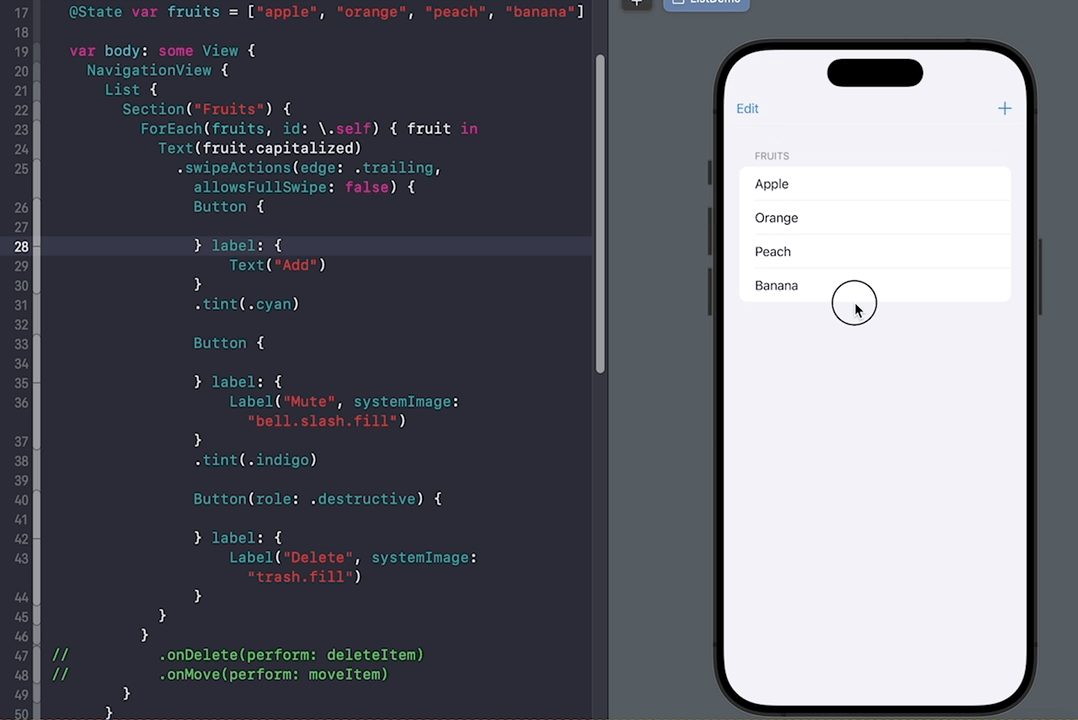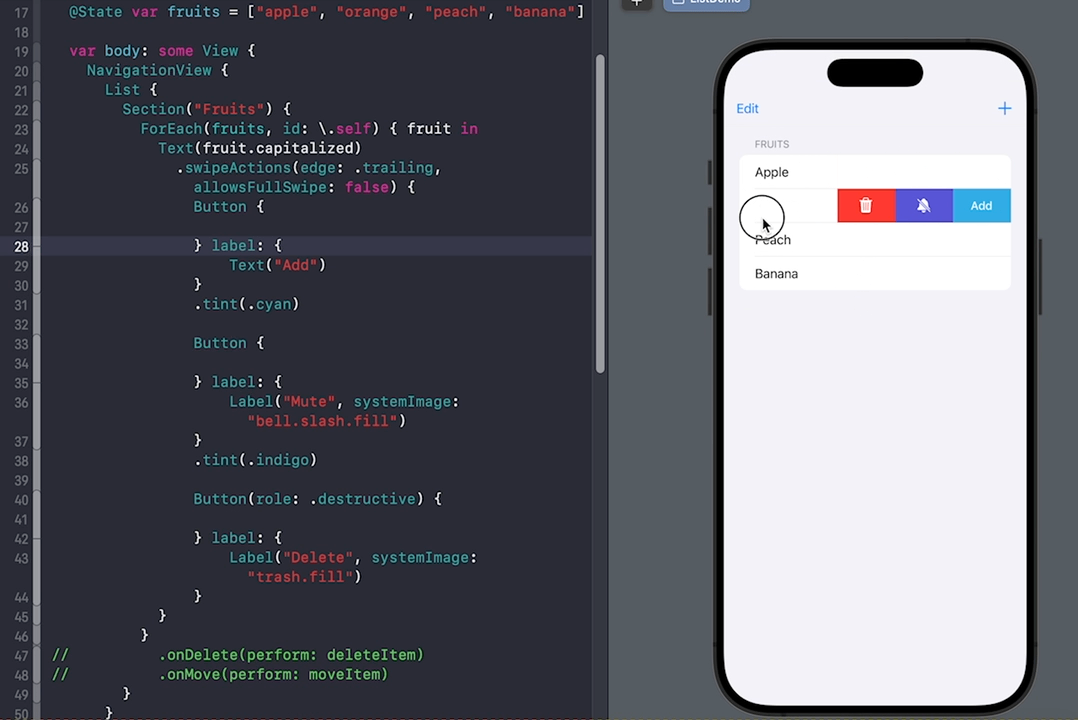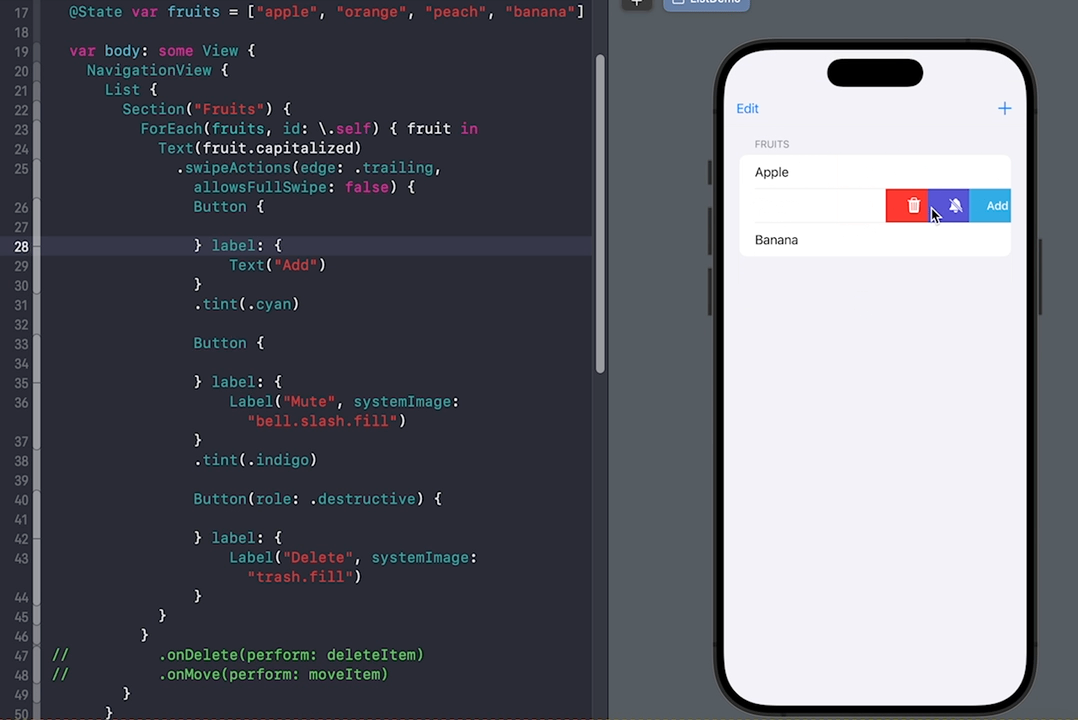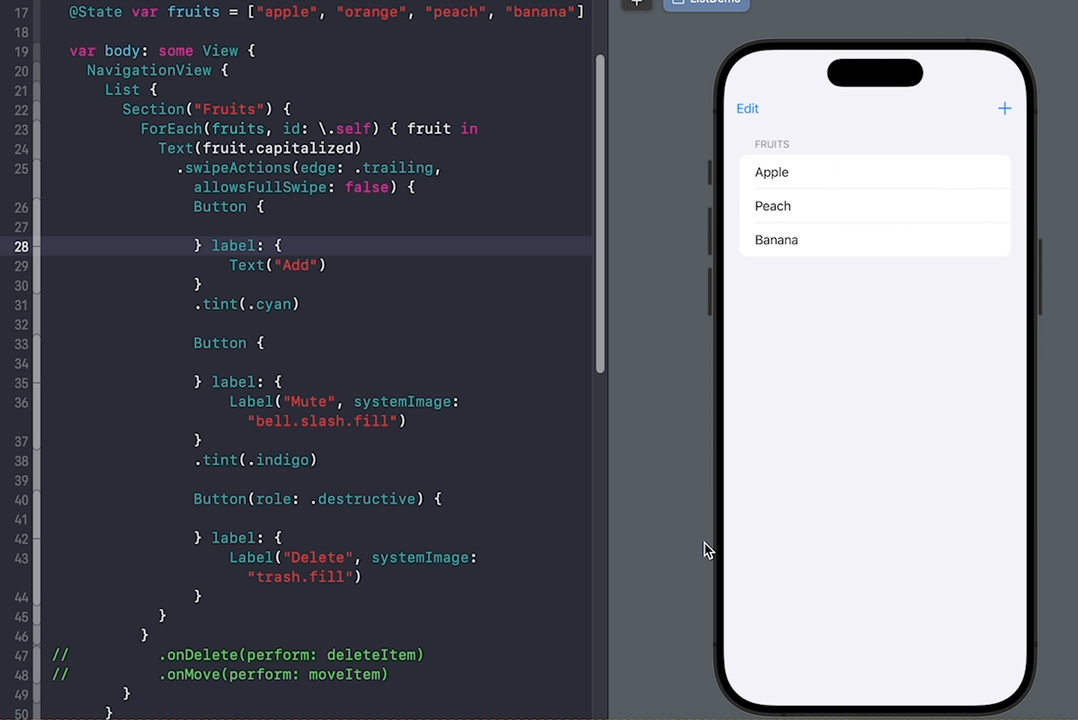
SwiftUI中List的liststyle样式及使用详解添加、移动、删除、自定义滑动
SwiftUI中的List可是个好东西,它用于显示可滚动列表的视图容器,类似于UITableView。在List中可以显示静态或动态的数据,并支持垂直滚动。List是一个数据驱动的视图,当数据发生变化时,列表会自动更新。针对List…...

PostgreSQL的系统视图pg_stats
PostgreSQL的系统视图pg_stats pg_stats 是 PostgreSQL 提供的一种系统视图,用于展示当前数据库中的统计信息。这些统计信息由数据库内部的自动统计过程通过 ANALYZE 命令收集,它们帮助查询规划器做出更好的执行决策,从而优化查询性能。 pg…...

UML2.0-系统架构师(二十四)
1、(重点)系统()在规定时间内和规定条件下能有效实现规定功能的能力。它不仅取决于规定的使用条件等因素,还与设计技术有关。 A可靠性 B可用性 C可测试性 D可理解性 解析: 可靠性:规定时间…...

leetcode 152. 乘积最大子数组「贪心」「动态规划」
152. 乘积最大子数组 题目描述: 给你一个整数数组nums,请你找出数组中乘积最大的非空连续子数组,并返回该子数组所对应的乘积 思路1:贪心 由于 n u m s [ i ] nums[i] nums[i]都是整数,所以多乘一些数肯定不会让绝…...

Android项目目录结构
Android项目目录结构 1. 顶层目录2. 重要的顶层文件和目录3. app模块目录结构4. 重要的**app**模块文件和目录5. 典型的 **build.gradle** 文件内容 典型的Android项目结构的详细介绍。 1. 顶层目录 MyAndroidApp/ ├── .gradle/ ├── .idea/ ├── app/ ├── build/ ├…...
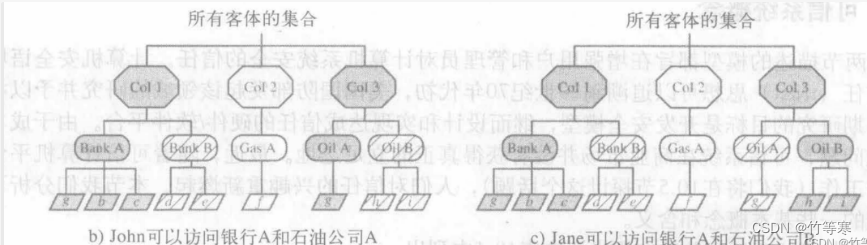
网络安全--计算机网络安全概述
文章目录 网络信息系统安全的目标网络安全的分支举例P2DR模型信息安全模型访问控制的分类多级安全模型 网络信息系统安全的目标 保密性 保证用户信息的保密性,对于非公开的信息,用户无法访问并且无法进行非授权访问,举例子就是:防…...

用requirements.txt配置环境
1. 在anaconda创建环境 创建Python版本为3.8的环境,与yolov5所需的包适配。 2. 在Anaconda Prompt中激活环境 (base) C:\Users\吴伊晴>conda activate yolov5 3. 配置环境 用指定路径中的requirements.txt配置环境。 (yolov5) C:\Users\吴伊晴>pip insta…...

APP渗透-android12夜神模拟器+Burpsuite实现
一、夜神模拟器下载地址:https://www.yeshen.com/ 二、使用openssl转换证书格式 1、首先导出bp证书 2、将cacert.der证书在kali中转换 使用openssl生成pem格式证书,并授予最高权限 openssl x509 -inform der -in cacert.der -out cacert.pem chmod 777 cacert…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

LabVIEW双光子成像系统技术
双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制,展现出显著的技术优势: 深层组织穿透能力:适用于活体组织深度成像 高分辨率观测性能:满足微观结构的精细研究需求 低光毒性特点:减少对样本的损伤…...

BLEU评分:机器翻译质量评估的黄金标准
BLEU评分:机器翻译质量评估的黄金标准 1. 引言 在自然语言处理(NLP)领域,衡量一个机器翻译模型的性能至关重要。BLEU (Bilingual Evaluation Understudy) 作为一种自动化评估指标,自2002年由IBM的Kishore Papineni等人提出以来,…...

LCTF液晶可调谐滤波器在多光谱相机捕捉无人机目标检测中的作用
中达瑞和自2005年成立以来,一直在光谱成像领域深度钻研和发展,始终致力于研发高性能、高可靠性的光谱成像相机,为科研院校提供更优的产品和服务。在《低空背景下无人机目标的光谱特征研究及目标检测应用》这篇论文中提到中达瑞和 LCTF 作为多…...

热门Chrome扩展程序存在明文传输风险,用户隐私安全受威胁
赛门铁克威胁猎手团队最新报告披露,数款拥有数百万活跃用户的Chrome扩展程序正在通过未加密的HTTP连接静默泄露用户敏感数据,严重威胁用户隐私安全。 知名扩展程序存在明文传输风险 尽管宣称提供安全浏览、数据分析或便捷界面等功能,但SEMR…...
