Python和MATLAB微机电健康推导算法和系统模拟优化设计
🎯要点
🎯惯性测量身体活动特征推导健康状态算法 | 🎯卷积网络算法学习惯性测量数据估计六自由度姿态 | 🎯全球导航卫星系统模拟,及惯性测量动态测斜仪算法、动态倾斜算法、融合算法 | 🎯微机电系统加速度计陀螺仪模拟优化 | 🎯微机电系统模拟优化设计
🍪语言内容分比


🍇MATLAB静电驱动微机电器件
微机电系统器件通常由悬挂在固定电极上方的可移动细梁或具有高纵横比的电极组成。驱动、切换和其他信号和信息处理功能可以利用在可移动电极和固定电极之间施加电压而引起的电极变形。最常见的微机电系统器件是悬挂在接地电极上方的一系列悬臂梁开关。
此示例使用以下几何结构来模拟微机电系统开关。顶部电极的长度为 150 μ m 150 \mu m 150μm,厚度为 2 μ m 2 \mu m 2μm。杨氏模量 E 为 170 G P a 170 GPa 170GPa,泊松比 u u u 为 0.34 。底部电极的长度为 50 μ m 50 \mu m 50μm,厚度为 2 μ m 2 \mu m 2μm,距离顶部电极最左端 100 μ m 100 \mu m 100μm。顶部和底部电极之间的间隙为 2 μ m 2μm 2μm。
在顶部电极和接地平面之间施加的电压会在导体表面感应出静电荷,进而导致静电力垂直作用于导体表面。由于接地平面是固定的,静电力只会使顶部电极变形。当梁变形时,电荷会在导体表面重新分布。由此产生的静电力和梁的变形也会发生变化。这个过程一直持续到系统达到平衡状态。
为简单起见,本示例使用基于松弛的算法而不是牛顿方法来耦合静电域和机械域。该示例遵循以下步骤:
- 使用可移动电极上的恒定电势 V0 解决非变形几何结构中的静电有限元分析问题。
- 使用沿可移动电极计算的电荷密度值计算机械解决方案的负载和边界条件。可动电极上的静电压力由下式给出
P = 1 2 e ∣ D ∣ 2 P=\frac{1}{2 e}|D|^2 P=2e1∣D∣2,其中, ∣ D ∣ |D| ∣D∣ 是电通量密度的大小, ϵ \epsilon ϵ 是可移动电极旁边的介电常数。
-
通过求解机械有限元分析问题来计算可移动电极的变形。
-
使用计算出的可移动电极的位移来更新沿可移动电极的电荷密度,
∣ D d e f ( x ) ∣ ≈ ∣ D 0 ( x ) ∣ G G − v ( x ) \left|D_{ def }(x)\right| \approx\left|D_0(x)\right| \frac{G}{G-v(x)} ∣Ddef(x)∣≈∣D0(x)∣G−v(x)G,其中 ∣ D def ( x ) ∣ \left|D_{\text {def }}(x)\right| ∣Ddef (x)∣ 是变形电极中电通量密度的大小, ∣ D 0 ( x ) ∣ \left|D_0(x)\right| ∣D0(x)∣ 是变形电极中电通量密度的大小未变形电极中的电通量密度, G G G 是在没有驱动的情况下可移动电极和固定电极之间的距离, v ( x ) v(x) v(x) 是可移动电极在位置 x x x 处沿其轴的位移。
- 重复步骤2-4,直到最后两次迭代中的电极变形值收敛。
在此示例的静电分析部分中,将计算电极周围的电势。首先,使用构造实体几何建模方法创建悬臂开关几何体。用于静电分析的几何体由三个矩形组成,用矩阵表示。矩阵的每一列描述了一种基本形状。
rect_domain = [3 4 1.75e-4 1.75e-4 -1.75e-4 -1.75e-4 ...-1.7e-5 1.3e-5 1.3e-5 -1.7e-5]';
rect_movable = [3 4 7.5e-5 7.5e-5 -7.5e-5 -7.5e-5 ...2.0e-6 4.0e-6 4.0e-6 2.0e-6]';
rect_fixed = [3 4 7.5e-5 7.5e-5 2.5e-5 2.5e-5 -2.0e-6 0 0 -2.0e-6]';
gd = [rect_domain,rect_movable,rect_fixed];
为每个基本形状创建一个名称。将名称指定为矩阵,其列包含基本形状矩阵中相应列的名称。
ns = char('rect_domain','rect_movable','rect_fixed');
ns = ns';
创建一个描述基本形状的并集和交集的公式。
sf = 'rect_domain-(rect_movable+rect_fixed)';
使用 decsg 函数创建几何图形。
dl = decsg(gd,sf,ns);
创建 PDE 模型并将几何包含在模型中。
model = createpde;
geometryFromEdges(model,dl);
绘制几何图形。
pdegplot(model,"EdgeLabels","on","FaceLabels","on")
xlabel("x-coordinate, meters")
ylabel("y-coordinate, meters")
axis([-2e-4,2e-4,-4e-5,4e-5])
axis square
该几何图形中的边数为:
- 可动电极:E3、E7、E11、E12
- 固定电极:E4、E8、E9、E10
- 域边界:E1、E2、E5、E6
将可移动电极设置为 20 V 的恒定电势值,将固定电极和域边界设置为 0 V。
V0 = 0;
V1 = 20;
applyBoundaryCondition(model,"dirichlet", ..."Edge",[4,8,9,10],"u",V0);
applyBoundaryCondition(model,"dirichlet", ..."Edge",[1,2,5,6],"u",V0);
applyBoundaryCondition(model,"dirichlet", ..."Edge",[3,7,11,12],"u",V1);
控制这个问题的偏微分方程是泊松方程,
− ∇ ⋅ ( ϵ ∇ V ) = ρ -\nabla \cdot(\epsilon \nabla V)=\rho −∇⋅(ϵ∇V)=ρ
其中 ϵ \epsilon ϵ是介电常数系数, ρ \rho ρ是电荷密度。只要介电常数恒定,介电常数就不会影响本例中的结果。假设域中不存在电荷,可以将泊松方程简化为拉普拉斯方程,
Δ V = 0 \Delta V=0 ΔV=0
📜泊松方程用例:Python低溫半导体电子束量子波算法计算
📜拉普拉斯方程用例:Python高压电容导电体和水文椭圆微分
指定系数。
specifyCoefficients(model,"m",0,"d",0,"c",1,"a",0,"f",0);
生成相对细的网格。
hmax = 5e-6;
generateMesh(model,"Hmax",hmax);
pdeplot(model)
xlabel("x-coordinate, meters")
ylabel("y-coordinate, meters")
axis([-2e-4, 2e-4,-4e-5, 4e-5])
axis square
求解模型
results = solvepde(model);
绘制外域的电势。
u = results.NodalSolution;
figure
pdeplot(model,"XYData",results.NodalSolution, ..."ColorMap","jet");title("Electric Potential");
xlabel("x-coordinate, meters")
ylabel("y-coordinate, meters")
axis([-2e-4,2e-4,-4e-5,4e-5])
axis square
在此示例的机械分析部分中,将计算可移动电极的变形。
👉参阅&更新:计算思维 | 亚图跨际
相关文章:

Python和MATLAB微机电健康推导算法和系统模拟优化设计
🎯要点 🎯惯性测量身体活动特征推导健康状态算法 | 🎯卷积网络算法学习惯性测量数据估计六自由度姿态 | 🎯全球导航卫星系统模拟,及惯性测量动态测斜仪算法、动态倾斜算法、融合算法 | 🎯微机电系统加速度…...

IT之家最新科技热点 | 小米 AI 研究院开创多模态通用模型
人不走空 🌈个人主页:人不走空 💖系列专栏:算法专题 ⏰诗词歌赋:斯是陋室,惟吾德馨 目录 🌈个人主页:人不走空 💖系列专栏:算法专题 ⏰诗词歌…...

黑色矩形块检测数据集VOC+YOLO格式2000张1类别
数据集格式:Pascal VOC格式YOLO格式(不包含分割路径的txt文件,仅仅包含jpg图片以及对应的VOC格式xml文件和yolo格式txt文件) 图片数量(jpg文件个数):2000 标注数量(xml文件个数):2000 标注数量(txt文件个数):2000 标注…...

Linux内存管理--系列文章柒——硬件架构
一、引子 之前文章讲解的是系统的虚拟内存,本章讲述这些硬件的架构和系统怎样统一管理这些硬件的。 二、物理内存模型 物理内存模型描述了计算机系统中的物理内存如何由操作系统组织和管理。它定义了物理内存如何划分为单元,如何寻址这些单元以及如何…...

QQ音乐Android一面凉经
最近面试了不少公司, 近期告一段落, 整理一下各家的面试问题, 打算陆续发布出来, 供有缘人参考。今天给大家带来的是QQ音乐Android一面凉经。 面试岗位: QQ音乐Android开发工程师面试时长: 50min(提问40min 反问10min)代码考核: 无 面试问题(40min) 自我介绍 工作经历, 重点…...
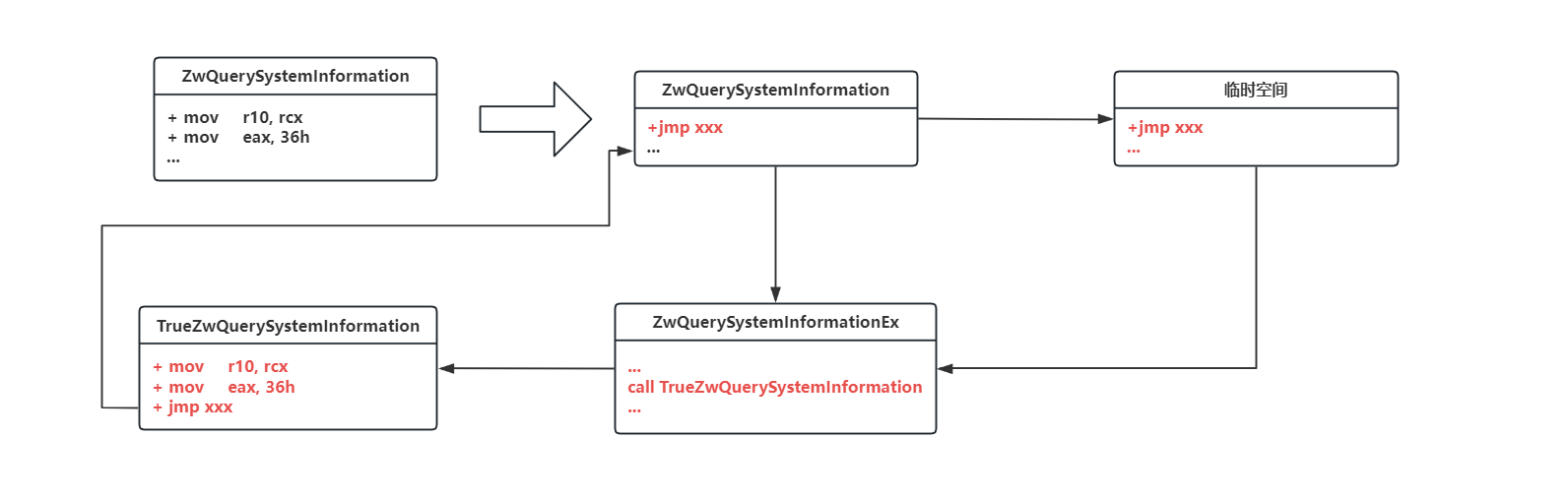
浅谈进程隐藏技术
前言 在之前几篇文章已经学习了解了几种钩取的方法 浅谈调试模式钩取浅谈热补丁浅谈内联钩取原理与实现导入地址表钩取技术 这篇文章就利用钩取方式完成进程隐藏的效果。 进程遍历方法 在实现进程隐藏时,首先需要明确遍历进程的方法。 CreateToolhelp32Snapsh…...
单元测试)
【C++】Google Test(gtest)单元测试
文章目录 Google Test(gtest)单元测试使用示例更多用法测试夹具 Google Test(gtest)单元测试 单元测试是一种软件测试方法,它旨在将应用程序的各个部分(通常是方法或函数)分离出来并独立测试&a…...

水箱高低水位浮球液位开关
水箱高低水位浮球液位开关概述 水箱高低水位浮球液位开关是一种用于监测和控制水箱中液位的自动化设备,它能够在水箱液位达到预设的高低限制时,输出开关信号,以控制水泵或电磁阀的开闭,从而维持水箱液位在一个安全的范围内。这类设…...

Autoware内容学习与初步探索(一)
0. 简介 之前作者主要是基于ROS2,CyberRT还有AutoSar等中间件完成搭建的。有一说一,这种从头开发当然有从头开发的好处,但是如果说绝大多数的公司还是基于现成的Apollo以及Autoware来完成的。这些现成的框架中也有很多非常好的方法。目前作者…...

【手写数据库内核组件】01 解析树的结构,不同类型的数据结构组多层的链表树,抽象类型统一引用格式
不同类型的链表 专栏内容: postgresql使用入门基础手写数据库toadb并发编程 个人主页:我的主页 管理社区:开源数据库 座右铭:天行健,君子以自强不息;地势坤,君子以厚德载物. 文章目录 不同类型…...

Pandas 进阶 —— 数据转换、聚合与可视化
引言 在数据分析的旅程中,Pandas 库提供了从数据转换到聚合再到可视化的全面解决方案。上篇我们掌握了数据的导入和清洗,本篇我们将探索如何通过 Pandas 对数据进行更高级的处理,包括数据转换、聚合分析以及可视化展示。 数据转换 数据转换…...

华为OD机试 - 来自异国的客人(Java 2024 D卷 100分)
华为OD机试 2024D卷题库疯狂收录中,刷题点这里 专栏导读 本专栏收录于《华为OD机试(JAVA)真题(D卷C卷A卷B卷)》。 刷的越多,抽中的概率越大,每一题都有详细的答题思路、详细的代码注释、样例测…...

期末上分站——计组(3)
复习题21-42 21、指令周期是指__C_。 A. CPU从主存取出一条指令的时间 B. CPU执行一条指令的时间 C. CPU从主存取出一条指令的时间加上执行这条指令的时间。 D. 时钟周期时间 22、微型机系统中外设通过适配器与主板的系统总线相连接,其功能是__D_。 A. 数据缓冲和…...

IDA*——AcWing 180. 排书
IDA* 定义 IDA*(Iterative Deepening A*)是一种结合了深度优先搜索(DFS)的递归深度限制特性和A搜索的启发式估价函数的搜索算法。它主要用于解决启发式搜索问题,尤其是当搜索空间很大或者搜索成本不确定时。 IDA* 是…...

【云计算】公有云、私有云、混合云、社区云、多云
公有云、私有云、混合云、社区云、多云 1.云计算的形态1.1 公有云1.2 私有云1.3 混合云1.4 社区云1.5 多云1.5.1 多云和混合云之间的关系1.5.2 多云的用途1.5.3 影子 IT 和多云1.5.4 优缺点 2.不同云形态的对比 1.云计算的形态 张三⾃⼰在家做饭吃,这是 私有云&…...

MySQL中的MVCC解析
MySQL中的MVCC解析 多版本并发控制是MySQL中实现高并发的一种关键技术。通过对数据进行多版本的管理,MVCC能够在保证数据一致性的同时,提高数据库的并发性能。本文将深入探讨MySQL中的MVCC机制,包括其原理、实现方式以及优势。 MVCC的原理 …...

【2024最新华为OD-C/D卷试题汇总】[支持在线评测] LYA的生日聚会(100分) - 三语言AC题解(Python/Java/Cpp)
🍭 大家好这里是清隆学长 ,一枚热爱算法的程序员 ✨ 本系列打算持续跟新华为OD-C/D卷的三语言AC题解 💻 ACM银牌🥈| 多次AK大厂笔试 | 编程一对一辅导 👏 感谢大家的订阅➕ 和 喜欢💗 …...

初识STM32:芯片基本信息
STM32简介 STM32是ST公司基于ARM公司的Cortex-M内核开发的32位微控制器。 ARM公司是全球领先的半导体知识产权(IP)提供商,全世界超过95%的智能手机和平板电脑都采用ARM架构。 ST公司于1987年由意大利的SGS微电子与法国的Thomson半导体合并…...
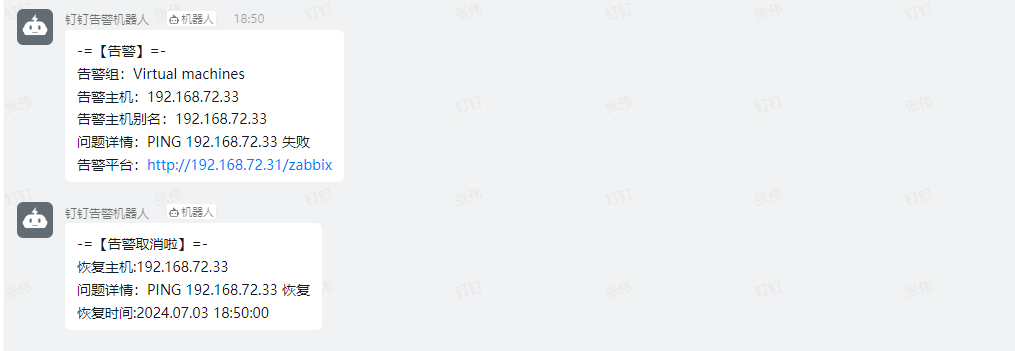
Zabbix 配置PING监控
Zabbix PING监控介绍 如果需要判断机房的网络或者主机是否正常,这就需要使用zabbix ping,Zabbix使用外部命令fping处理ICMP ping的请求,在基于ubuntu APT方式安装zabbix后默认已存在fping程序。另外zabinx_server配置文件参数FpingLocation默…...
-- Wandb fails with ServiceStartProcessError)
异常解决(三)-- Wandb fails with ServiceStartProcessError
原文链接:https://github.com/wandb/wandb/issues/5765 我的环境配置: Python3.8.16 Wandb0.17.4 在使用Wandb记录实验数据时, 报以下错误: ServiceStartProcessError: The wandb service process exited with 1. Ensure that s…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...

Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术解析
Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术解析 一、第一轮基础概念问题 1. Spring框架的核心容器是什么?它的作用是什么? Spring框架的核心容器是IoC(控制反转)容器。它的主要作用是管理对…...
