第17章 关于局部波动率的一些总结
这学期会时不时更新一下伊曼纽尔·德曼(Emanuel Derman) 教授与迈克尔B.米勒(Michael B. Miller)的《The Volatility Smile》这本书,本意是协助导师课程需要,发在这里有意的朋友们可以学习一下,思路不一定够清晰且由于分工原因我是从书本第13章写起,还请大家见谅。
第17章 关于局部波动率的一些总结
局部波动率的优点和缺点
优点
在布莱克-斯科尔斯-默顿(BSM)模型的所有扩展式中,局部波动率模型是能够解释波动率微笑曲线的最简单模型。通过标的股票价格和时间的函数来描述股票的波动率,我们可以得到 σ(S,t)\sigma(S,t)σ(S,t),并使其满足某个市场的隐含波动率曲面 Σ(S,t,K,T)\Sigma(S,t,K,T)Σ(S,t,K,T),这相当于是用一个统一的波动率流程替代大量不同的 BSM 隐含波动率
dSS=μdt+σ(S,t)dZ\frac{dS}{S}=\mu dt+\sigma(S,t)dZ SdS=μdt+σ(S,t)dZ
若 σ(S,t)\sigma(S,t)σ(S,t) 已知,通过复制原理可以推导股票型期权BSM偏微分方程的扩展式:
∂C∂t+∂C∂SrS+12σ(S,t)2S2∂2C∂S2=rC\frac{\partial C}{\partial t}+\frac{\partial C}{\partial S}rS+\frac{1}{2}\sigma(S,t)^2S^2\frac{\partial^2C}{\partial S^2}=rC ∂t∂C+∂S∂CrS+21σ(S,t)2S2∂S2∂2C=rC
明确了局部波动率的函数式后,就可以用局部波动率模型得到无套利机会的期权价格,也可以计算得到标准期权和奇异期权的对冲比率。这类模型一个非常好的优势在于,它跟初始的 BSM 模型及其变化的联系非常密切。BSM隐含波动率等于初始股票价格和行权价格之间的局部波动率的平均数,这一概念可以有很多直观的经验法则,比如在有斜度的情况下,期权价值和对冲比率跟 BSM 模型中(斜度等于0)的结果有什么差异。正是由于这些原因,局部波动率模型在学术界和市场上都越来越流行
关键问题
问题:局部波动率模型是否能够较好地反映真实的情况?模型中标的资产的变动及其波动率是否能描述目标市场的实际走势?标的资产的变动情况是否服从下面这个随机微分方程?
dSS=μdt+σ(S,t)dZ\frac{dS}{S}=\mu dt+\sigma(S,t)dZ SdS=μdt+σ(S,t)dZ
我们需要的效果是,模型的结果在实际期权估值和对冲方面确实是有用的。不同标的资产市场(股票、固定收益、商品等)的变动情况在局部波动率模型中都可以有所体现
缺点
1、需要定期不断再调整
随着时间流逝,标的股票价格或者指数水平会发生变化,隐含波动率曲面也会发生变化,因此需要从这些数据中提取新的局部波动率曲面模型。而根据新的曲面,对冲比率和奇异期权的价值需要重新计算,模型的参数并不是静态的
2、无法描述短期斜度
局部波动率模型很难用来描述未来的短期斜度。要理解这一点,我们可以用单因子短期利率期限结构模型来分析短期利率的变动情况
就一条典型的收益率曲线而言,短期收益率是向上倾斜的,而 20 年以上的长期收益率会逐渐平坦。因此在单因子期限结构模型中,对于利率期限的调整是,令利率树形图上的短期平均利率逐步升高,而20年以上的长期利率不变。这就意味着,在这个经调整的模型中,期限为20年以上的收益率曲线变得相对平坦,而不再是向上倾斜。如果在期限结构模型中所做的假设是无偏的,也就是说令期限为 20 年以内的收益率也是相对平坦的,这就会使分析结果出现问题,因为20年以内的收益率曲线通常应该是向上倾斜的
局部波动率模型在处理短期斜度的时候也会出现类似现象,但是影响主要是并联关系而不是串联关系。以行权价为维度来看股票指数期权,期限较短的期权对应的隐含波动率斜度更陡峭,而期限较长的期权对应的隐含波动率更平坦。要根据这一斜度变化的情况来调整局部波动率模型,就需要考虑在未来使短期的波动率斜度变得更平坦化。如果当前的短期斜度总是陡峭的,而坚持在模型中令未来的短期斜度保持平坦,那么分析结果也会出现问题
指数期权的局部波动率模型检验
期权模型取决于能否构建一个无风险的对冲策略。且该策略的损益(P&L)的方差等于0,因此是否是好模型的判断标准之一就是,通过模型得到的对冲比率能否将一个对冲组合的损益方差降到最低。如果复制是绝对精确的,那么一个对冲组合的损益方差应该等于0
不同市场结构对于对冲组合损益方差的影响
假设有一个看涨期权 CCC,通过卖出标的股票 SSS 对其进行delta对冲。我们可以选择用BSM对冲比率 ΔBSM\Delta_{BSM}ΔBSM 或者局部波动率对冲比率 Δloc\Delta_{loc}Δloc 对其进行瞬时对冲。相应的对冲组合价值为:
πBSM=C−ΔBSMSπloc=C−ΔlocS\pi_{BSM}=C-\Delta_{BSM}S\\ \pi_{loc}=C-\Delta_{loc}S πBSM=C−ΔBSMSπloc=C−ΔlocS
如果标的股票价格发生变动 dSdSdS,局部波动率对冲组合的损益和BSM对冲组合的损益差就等于:
dπloc−dπBSM=(ΔBSM−Δloc)dS=εdSd\pi_{loc}-d\pi_{BSM}=(\Delta_{BSM}-\Delta_{loc})dS=\varepsilon dS dπloc−dπBSM=(ΔBSM−Δloc)dS=εdS
此处假设期权的市场价值变动 dCdCdC 在两个方案下都是相等的。在之前的章节中我们用链式法则证明过如下的关系式:
Δloc≈ΔBSM−VBSMβ\Delta_{loc}\approx\Delta_{BSM}-V_{BSM}\beta Δloc≈ΔBSM−VBSMβ
其中 VBSMV_{BSM}VBSM 表示BSM中的vega值,β\betaβ 表示隐含波动率方程中的负斜度绝对值(此处 β\betaβ 是正数)。由于 VBSMV_{BSM}VBSM 也是正数,当斜度为负时,Δloc\Delta_{loc}Δloc 就会小于 ΔBSM\Delta_{BSM}ΔBSM,因此:
ε=ΔBSM−Δloc>0\varepsilon=\Delta_{BSM}-\Delta_{loc}>0 ε=ΔBSM−Δloc>0
delta对冲的损益在很短的时间间隔 dtdtdt 内取决于实际波动率 σR\sigma_RσR,且存在如下关系式:
dπBSM=12ΓBSS2(σR2−σBSM2)dtdπloc=12ΓlocS2(σR2−σloc2(S,t))dtd\pi_{BSM}=\frac{1}{2}\Gamma_{BS}S^2(\sigma_R^2-\sigma_{BSM}^2)dt\\ d\pi_{loc}=\frac{1}{2}\Gamma_{loc}S^2(\sigma_R^2-\sigma_{loc}^2(S,t))dt dπBSM=21ΓBSS2(σR2−σBSM2)dtdπloc=21ΓlocS2(σR2−σloc2(S,t))dt
其中 σBSM\sigma_{BSM}σBSM 表示期权的BSM隐含波动率,σloc(S,t)\sigma_{loc}(S,t)σloc(S,t) 表示在隐含树形图中股价等于 SSS、时间等于 ttt 时的局部波动率。若BSM模型正确,则上述第一个式子中的损益变动值就等于0;若局部波动率模型正确,则上述第二个式子中的损益变动值等于0。若两个都不是绝对正确,则应该选择损益变动值最小的模型
如果股票价格变动 dSdSdS,同时时间增加 dtdtdt,则根据下面三式:
dπloc−dπBSM=(ΔBSM−Δloc)dS=εdSdπloc=12ΓlocS2(σR2−σloc2(S,t))dtd\pi_{loc}-d\pi_{BSM}=(\Delta_{BSM}-\Delta_{loc})dS=\varepsilon dS\\ d\pi_{loc}=\frac{1}{2}\Gamma_{loc}S^2(\sigma_R^2-\sigma_{loc}^2(S,t))dt dπloc−dπBSM=(ΔBSM−Δloc)dS=εdSdπloc=21ΓlocS2(σR2−σloc2(S,t))dt
可以得到:
dπBSM=dπloc−εdS=12ΓlocS2[σR2−σloc2(S,t)]dt−εdSd\pi_{BSM}=d\pi_{loc}-\varepsilon dS=\frac{1}{2}\Gamma_{loc}S^2[\sigma_R^2-\sigma_{loc}^2(S,t)]dt-\varepsilon dS dπBSM=dπloc−εdS=21ΓlocS2[σR2−σloc2(S,t)]dt−εdS
BSM对冲的总误差包含两项,第1项来自于波动率预测的偏差,第2项来自于delta对冲操作的偏差。第1项是由于波动率的变动,是一个二次非定向式,其符号只取决于波动率的误差 [σR2−σloc2(S,t)][\sigma_R^2-\sigma_{loc}^2(S,t)][σR2−σloc2(S,t)]。第2项是由于 delta 对冲的误差,是一个线性定向式。因为 ε\varepsilonε 是正数,其符号只取决于 dSdSdS 的符号
Crepey (2004) 曾经用4个不同市场结构来检验上式的效果,他将这4个市场结构分成两个维度,如下表所示:在下一个时间阶段,指数可以上行或下行,实际波动率可以高于或者低于当前的局部波动率
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-2OEUx0db-1678768931417)(C:\Users\Mei'xu'chen\AppData\Roaming\Typora\typora-user-images\image-20230314123213464.png)]](https://img-blog.csdnimg.cn/3416954f43cd4739b7c4211ae10f70fe.png)
dπBSM=dπloc−εdS=12ΓlocS2[σR2−σloc2(S,t)]dt−εdSd\pi_{BSM}=d\pi_{loc}-\varepsilon dS=\frac{1}{2}\Gamma_{loc}S^2[\sigma_R^2-\sigma_{loc}^2(S,t)]dt-\varepsilon dS dπBSM=dπloc−εdS=21ΓlocS2[σR2−σloc2(S,t)]dt−εdS
对于高波动率的下行市场(快速下跌),上式右侧的两项均导致 dπBSMd\pi_{BSM}dπBSM 上升,于是由波动率变动以及指数价格变动导致的对冲误差的作用效果互相强化,因此最终导致的BSM对冲误差 dπBSMd\pi_{BSM}dπBSM 为正数。对于低波动率的上行市场(缓慢上涨),两项都会导致 dπBSMd\pi_{BSM}dπBSM 下降,于是 dπBSMd\pi_{BSM}dπBSM 为负数。因此,在一个典型的指数市场上,BSM对冲比率通常不等于0。与此相反,如果是缓慢下跌或者快速上涨,两项的变动效果会相互抵消,因此对冲误差会减小。但对于BSM模型来说,指数市场的这种变动方式(缓慢下跌或者快速上涨,这是对冲误差很小的两种市场结构)并不常见。总结而言,BSM 对冲策略的表现可能会更糟糕一些——在典型的股票指数市场中,对冲组合损益的波动会更加剧烈。因此,我们认为对于股票指数市场而言,BSM 模型的表现要逊于局部波动率模型的表现。Crepey(2004)根据市场历史数据分析了对冲组合的损益情况,其结论也支持这一观点。我们再次强调,很显然,在用这种模型进行对冲之前,需要不断地进行模型调整
相关文章:

第17章 关于局部波动率的一些总结
这学期会时不时更新一下伊曼纽尔德曼(Emanuel Derman) 教授与迈克尔B.米勒(Michael B. Miller)的《The Volatility Smile》这本书,本意是协助导师课程需要,发在这里有意的朋友们可以学习一下,思…...

反转链表合并两个有序链表链表分割链表的回文结构相交链表
反转链表来源:杭哥206. 反转链表 - 力扣(LeetCode)typedef struct ListNode ListNode; struct ListNode* reverseList(struct ListNode* head) {if (headNULL){return NULL;}ListNode* prevhead;ListNode* curhead->next;ListNode* furNUL…...

联想触摸板只能单击,二指三指失效
问题背景 这问题是我笔记本两三年前重装win10系统后出现的,当时有鼠标懒得弄。今天发现没鼠标后,触摸板连二指滑动都没有太麻烦了,所以决定弄一下。 联想笔记本,win10系统重装后出现的问题。 1.鲁大师,联想电脑管家 …...
卡死解决办法)
mysql 删除表卡死,或是截断(truncate)卡死解决办法
利用工具进行truncate表的时候,一直运行,运行了十几分钟也没有成功。中止之后再运行也是一样。但是删除表的数据以及查询表数据都是可以的。猜测是锁死了。 使用 show processlist; 发现Waiting for table metadata lock 问题; mysql> s…...
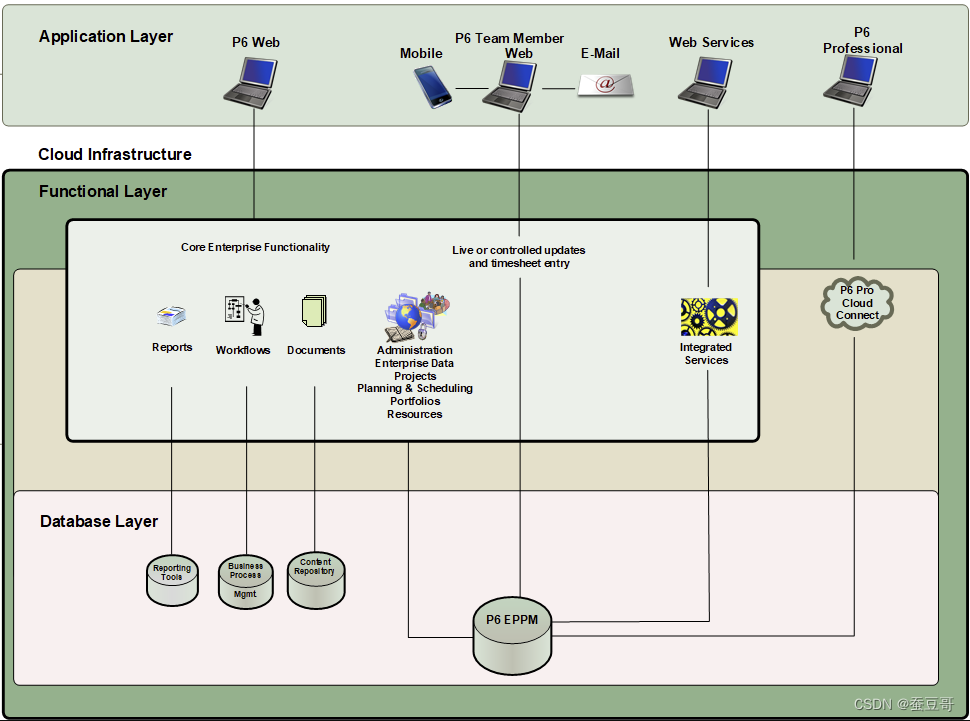
ORACLE P6 EPPM 架构及套件介绍(源自Oracle Help)
引言 借助官方帮助的内容, 我水一篇文章,翻译了下文 P6EPPM架构 P6各套件 P6:大多数用户几乎完全依赖在标准网络浏览器中运行的 P6 网络应用程序。简称为 P6,它是管理项目的主要界面。P6 移动版:允许团队成员提供任…...

Android开发面试:数据结构与算法知识答案精解
目录 数据结构与算法 线性表 数组 链表 栈 队列 树 二叉树 红黑树 哈夫曼树 排序算法 冒泡排序 选择排序 插入排序 希尔排序 堆排序 快速排序 归并排序 查找算法 线性查找 二分查找 插值查找 斐波拉契查找 树表查找 分块查找 哈希查找 动态规划算法…...

京东前端手写面试题集锦
实现call方法 call做了什么: 将函数设为对象的属性执行和删除这个函数指定this到函数并传入给定参数执行函数如果不传入参数,默认指向为 window // 模拟 call bar.mycall(null); //实现一个call方法: // 原理:利用 context.xxx self obj.…...

【JDK动态代理】及【CGLib动态代理】:Java的两种动态代理方式
Java的两种动态代理方式动态代理是什么?JDK动态代理CGLib动态代理CGLib 底层原理CGLib 实现步骤两者区别Spring AOP原理--动态代理动态代理是什么? 动态代理就是,在程序运行期,创建目标对象的代理对象,并对目标对象中的…...

《程序员面试金典(第6版)》面试题 04.05. 合法二叉搜索树
题目描述 实现一个函数,检查一棵二叉树是否为二叉搜索树。 示例 1: 输入: 2/ \1 3输出: true 示例 2: 输入: 5/ \1 4/ \3 6输出: false 解释: 输入为: [5,1,4,null,null,3,6]。 根节点的值为 5 ,但是其右子节点值为 4 。 解题思路与代码 使用…...

Nginx 反向代理技术梳理
Nginx 反向代理技术梳理 使用反向代理脑图 域名 A 可以解析找到 CDN 缓存 用户点击 APP 即通过 URL 发送 HTTPS 请求域名会进入阿里云的 DNS 服务器,解析域名会做第一级负载均衡通过 CDN 解析出域名,通过阿里云配置转发到 CDN 缓存服务器 CDN 有数据则直…...
 | 机试题+算法思路+考点+代码解析 【2023】)
华为OD机试 - 整数编码(Java) | 机试题+算法思路+考点+代码解析 【2023】
整数编码 题目 实现一种整数编码方法,使得待编码的数字越小,编码后所占用的字节数越小。 编码规则如下: 1、编码时7位一组,每个字节的低7位用于存储待编码数字的补码。 2、字节的最高位表示后续是否还有字节,置1表示后面还有更多的字节,置0表示当前字节为最后一个字…...

蓝桥杯冲击01 - 质数篇
目录 前言 一、质数是什么 二、易错点 三、试除法判断是否为质数 四、质数常考三大模型 五、真题练手 前言 距离蓝桥杯还有一个月,高效复习蓝桥杯知识, 质数相关的题目在蓝桥杯中经常出现。例如,2016年蓝桥杯省赛初赛第四题就是要求判…...

【WEB前端进阶之路】 HTML 全路线学习知识点梳理(下)
前言 本文是HTML零基础小白学习系列的第三篇文章,点此阅读 上一篇文章 文章目录前言十五.HTML布局1.使用div元素添加网页布局2.使用table元素添加网页布局十六.HTML表单和输入1.文本域2.密码字段3.单选按钮4.复选框5.提交按钮十七.HTML框架1.iframe语法2.iframe设置…...
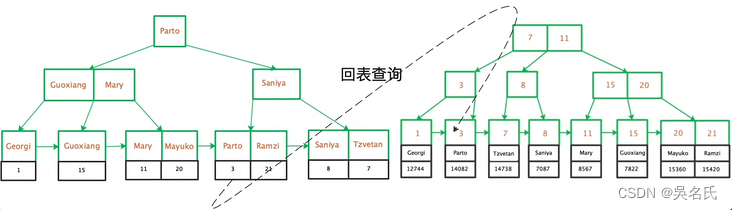
MySQL索引分类
1 MySQL索引都有哪些分类按数据结构分类可分为:Btree索引、Hash索引、Full-text索引;按物理存储分类可分为:聚簇索引、二级索引(辅助索引);按字段特性分类可分为:主键索引、普通索引、前缀索引;按字段个数分类可分为&a…...

会声会影2023最新版图文安装详细教程
会声会影2023操作简单,使用便捷,创意十足,新增的分屏功能,轨道透明度,镜头平移等功能,让用户的剪辑过程更加流畅,轻松就能制作出令人惊艳的视频作品。它不仅符合家庭或个人所需的影片剪辑功能&a…...
Java中的反射
类加载器(1)类的加载当我们的程序在运行后,第一次使用某个类的时候,会将此类的class文件读取到内存,并将此类的所有信息存储到一个Class对象中。说明:a.图中的Class对象是指:java.lang.Class类的…...

STM32入门笔记(03):STM32F103C8T6定时器的输入捕获模式和编码器模式(SPL库函数版)
目录1.定时器的输入捕获模式定时器输入捕获实验代码实现程序说明实现思路实现效果知识要点2.定时器的编码器模式定时器编码器实验代码实现实验思路知识要点参考资料先导知识 [1] STM32入门笔记(02):定时器之定时器中断、输入捕获和PWM输出(SPL库函数版)…...
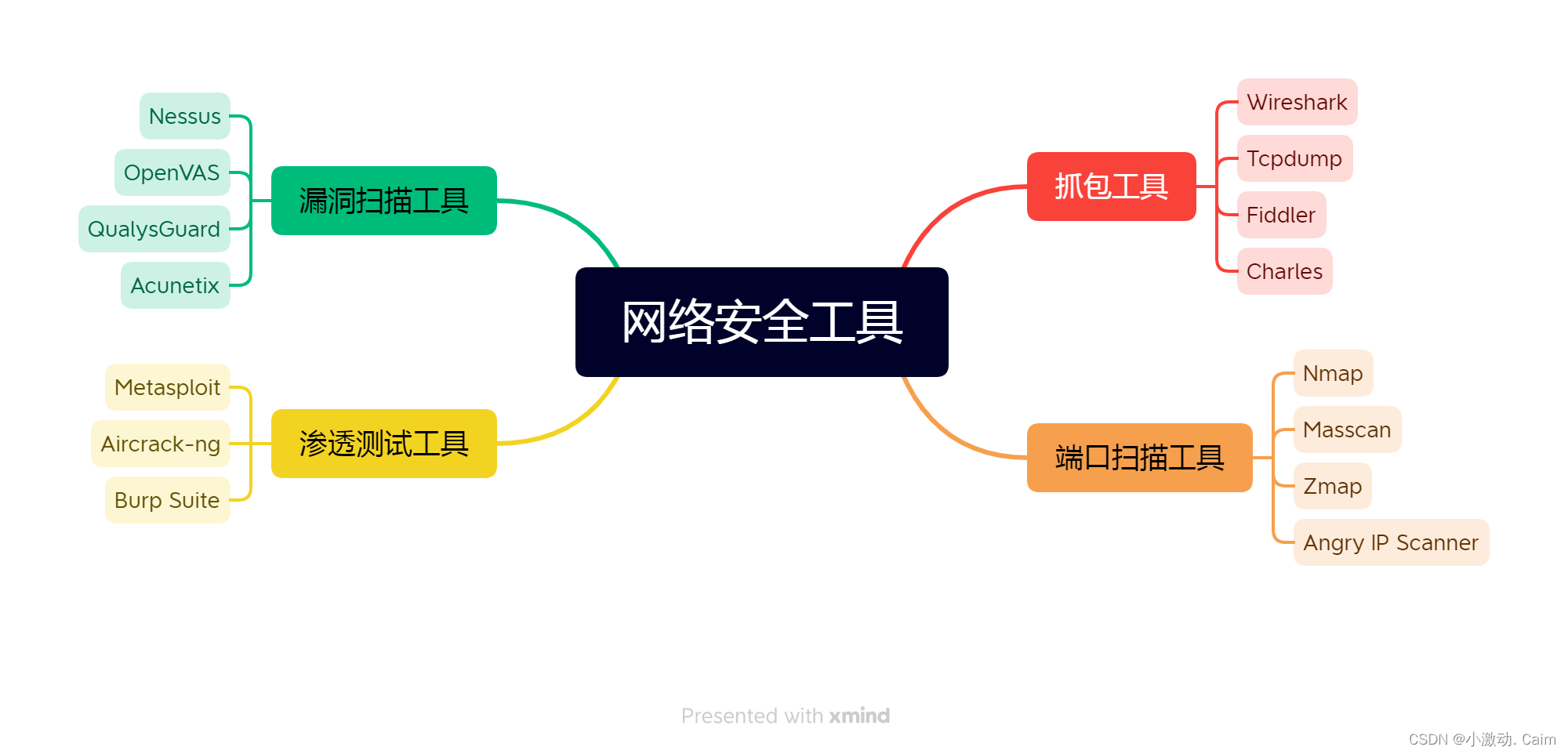
《网络安全》零基础教程-适合小白科普
《网络安全》零基础教程 目录 目录 《网络安全》零基础教程 第1章 网络安全基础 什么是网络安全 常见的网络安全威胁 网络安全的三个基本要素 网络安全的保障措施 第2章 网络攻击类型 病毒、蠕虫、木马、后门 DoS、DDoS攻击 SQL注入、XSS攻击 …...

微信小程序语言与web开发语言的区别
WXML与HTML的区别def:WXML是小程序框架设计的一套标签语言,用来构建小程序页面的结构,作用类似于web开发中的HTML区别:标签名称的不同如HTML中的div,span,img,a分别对应wxml中的view,…...
【2022-09-14】米哈游秋招笔试三道编程题
第一题:最短子串 题目描述 米小游拿到了一个字符串,她想截取一个连续子串,使得该子串中包含至少k个连续的“mihoyo”。 你可以帮米小游求出最短的子串长度,以及对应的子串位置吗? 输入描述 第一行输入两个正整数n…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...
