计算样本之间的相似度
文章目录
- 前言
- 一、距离度量
- 1.1 欧几里得距离(Euclidean Distance)
- 1.2 曼哈顿距离(Manhattan Distance)
- 1.3 切比雪夫距离(Chebyshev Distance)
- 1.4 闵可夫斯基距离(Minkowski Distance)
- 1.5 余弦距离(Cosine Distance)
- 代码演示
- 总结
- 二、相似度度量
- 2.1 余弦相似度(Cosine Similarity)
- 2.2 皮尔逊相关系数(Pearson Correlation Coefficient)
- 2.3 杰卡德相似系数(Jaccard Similarity Coefficient)
- 2.4 汉明距离(Hamming Distance)
- 2.5 相关距离(Correlation Distance)
- 代码演示
- 总结
前言
计算样本之间的相似度通常可以通过计算样本之间的距离来实现,尽管这不是唯一的方法。距离度量和相似度度量是两个相关但不同的概念。距离度量通常用于表示样本之间的不相似程度,而相似度度量则用于表示样本之间的相似程度。
一、距离度量
1.1 欧几里得距离(Euclidean Distance)
欧氏距离是两个点在 n 维空间中直线距离的度量。它是最常见的距离度量方法之一,用于计算两个向量之间的距离。
1.2 曼哈顿距离(Manhattan Distance)
曼哈顿距离,又称为城市街区距离,是指两个点在 n 维空间中各个坐标轴上的距离之和。
1.3 切比雪夫距离(Chebyshev Distance)
切比雪夫距离,又称为棋盘距离,是指两个点在 n 维空间中各个坐标轴上的最大距离。
1.4 闵可夫斯基距离(Minkowski Distance)
闵可夫斯基距离是欧氏距离和曼哈顿距离的广义形式,通过调整参数 𝑝,可以得到不同的距离度量。
1.5 余弦距离(Cosine Distance)
通过计算两个样本点之间夹角的余弦值的补值来衡量相似度。
代码演示
import numpy as np
from sklearn.metrics.pairwise import euclidean_distances, manhattan_distances
from scipy.spatial.distance import chebyshev, minkowski, cosine# 示例向量
vector1 = np.array([1.2, 2.3, 3.4, 4.5])
vector2 = np.array([4.1, 5.2, 6.3, 7.4])# 欧几里得距离
euclidean_dist = euclidean_distances([vector1], [vector2])
print(f'Euclidean Distance: {euclidean_dist[0][0]}')# 曼哈顿距离
manhattan_dist = manhattan_distances([vector1], [vector2])
print(f'Manhattan Distance: {manhattan_dist[0][0]}')# 切比雪夫距离
chebyshev_dist = chebyshev(vector1, vector2)
print(f'Chebyshev Distance: {chebyshev_dist}')# 闵可夫斯基距离(p=3)
minkowski_dist = minkowski(vector1, vector2, p=3)
print(f'Minkowski Distance (p=3): {minkowski_dist}')# 余弦相似度
cosine_dist = cosine(vector1, vector2)
print(f'Cosine Distance: {cosine_dist}')总结
在距离度量的五种方法中,欧几里得距离(Euclidean Distance)、曼哈顿距离(Manhattan Distance)、余弦距离 是最常用的三种。
欧几里得距离:适用于低维和中维数据,广泛用于各种机器学习算法。(低维通常在1-10维之间,中维在10—100之间)
曼哈顿距离:适用于高维数据,尤其是特征独立时。(高维>100维)
余弦距离:适用于高维稀疏数据,特别是文本数据和推荐系统。
二、相似度度量
2.1 余弦相似度(Cosine Similarity)
衡量两个向量的方向相似度,而不关注它们的大小。
2.2 皮尔逊相关系数(Pearson Correlation Coefficient)
衡量两个变量之间的线性相关性。
2.3 杰卡德相似系数(Jaccard Similarity Coefficient)
衡量两个集合的交集与并集的比值,常用于文本或集合相似度。
2.4 汉明距离(Hamming Distance)
计算两个样本在相同位置上不同元素的数量,常用于二进制数据。
2.5 相关距离(Correlation Distance)
计算两个变量之间的相关性,反映了两个向量在统计上的相似程度,是皮尔逊相关系数的补数。
代码演示
import numpy as np
from sklearn.metrics.pairwise import cosine_similarity
from scipy.spatial.distance import correlation, jaccard, hamming
from scipy.stats import pearsonr# 示例向量
vector1 = np.array([1.2, 2.3, 3.4, 4.5])
vector2 = np.array([4.1, 5.2, 6.3, 7.4])# 1. 余弦相似度(Cosine Similarity)
cosine_sim = cosine_similarity([vector1], [vector2])
print(f'Cosine Similarity: {cosine_sim[0][0]}')# 2. 皮尔逊相关系数(Pearson Correlation Coefficient)
pearson_corr, _ = pearsonr(vector1, vector2)
print(f'Pearson Correlation Coefficient: {pearson_corr}')# 3. 杰卡德相似系数(Jaccard Similarity Coefficient)
# 将向量转为布尔型(示例中使用大于2的值作为示例)
vector1_bool = vector1 > 2
vector2_bool = vector2 > 2
jaccard_sim = 1 - jaccard(vector1_bool, vector2_bool)
print(f'Jaccard Similarity Coefficient: {jaccard_sim}')# 4. 汉明距离(Hamming Distance)
# 这里的计算汉明距离先计算不相似度,再计算相似度
hamming_dist = hamming(vector1_bool, vector2_bool)
print(f'Hamming Distance: {hamming_dist}')
hamming_sim = 1 - hamming_dist
print(f'Hamming Similarity: {hamming_sim}')# 5. 相关距离(Correlation Distance)
# 这里的计算相关距离先计算不相似度,再计算相似度
correlation_dist = correlation(vector1, vector2)
correlation_sim = 1 - correlation_dist
print(f'Correlation Similarity: {correlation_sim}')总结
在相似度度量的五种常见方法中,余弦相似度(Cosine Similarity) 和 皮尔逊相关系数(Pearson Correlation Coefficient) 是最常用的两种。
余弦相似度:适用于高维稀疏数据,如文本数据和推荐系统。
皮尔逊相关系数:适用于数值数据,衡量线性相关性。
相关文章:

计算样本之间的相似度
文章目录 前言一、距离度量1.1 欧几里得距离(Euclidean Distance)1.2 曼哈顿距离(Manhattan Distance)1.3 切比雪夫距离(Chebyshev Distance)1.4 闵可夫斯基距离(Minkowski Distance)…...

2-5 softmax 回归的简洁实现
我们发现通过深度学习框架的高级API能够使实现线性回归变得更加容易。 同样,通过深度学习框架的高级API也能更方便地实现softmax回归模型。 本节如在上节中一样, 继续使用Fashion-MNIST数据集,并保持批量大小为256。 import torch from torc…...

我 17 岁创业,今年 20 岁,月入 70 万,全靠低代码
想象一下,当你还在高中的课桌前埋头苦读时,有人告诉你三年后你将成为一家年收入超过 100 万美元的科技公司的创始人。 听起来是不是像天方夜谭? 但对于 20 岁的小伙子 Jacob Klug 来说,这就是他的真实人生。 在大多数同龄人还在为…...

【Python】已解决:urllib.error.HTTPError: HTTP Error 403: Forbidden
文章目录 一、分析问题背景二、可能出错的原因三、错误代码示例四、正确代码示例五、注意事项 已解决:urllib.error.HTTPError: HTTP Error 403: Forbidden 一、分析问题背景 在使用Python的urllib库中的urlopen或urlretrieve函数下载文件时,有时会遇到…...

昇思12天
FCN图像语义分割 1. 主题和背景 FCN是由UC Berkeley的Jonathan Long等人于2015年提出的,用于实现图像的像素级预测。 2. 语义分割的定义和重要性 语义分割是图像处理和机器视觉中的关键技术,旨在对图像中的每个像素进行分类。它在很多领域有重要应用…...

【postgresql】 基础知识学习
PostgreSQL是一个高度可扩展的开源对象关系型数据库管理系统(ORDBMS),它以其强大的功能、灵活性和可靠性而闻名。 官网地址:https://www.postgresql.org/ 中文社区:文档目录/Document Index: 世界上功能最强大的开源…...

按键控制LED流水灯模式定时器时钟
目录 1.定时器 2. STC89C52定时器资源 3.定时器框图 4. 定时器工作模式 5.中断系统 1)介绍 2)流程图:编辑 3)STC89C52中断资源 4)定时器和中断系统 5)定时器的相关寄存器 6.按键控制LED流水灯模…...

【Docker安装】OpenEuler系统下部署Docker环境
【Docker安装】OpenEuler系统下部署Docker环境 前言一、本次实践介绍1.1 本次实践规划1.2 本次实践简介二、检查本地环境2.1 检查操作系统版本2.2 检查内核版本2.3 检查yum仓库三、卸载Docker四、部署Docker环境4.1 配置yum仓库4.2 检查可用yum仓库4.3 安装Docker4.4 检查Docke…...

小程序 使用 UI 组件 Vant Weapp 、vant组件样式覆盖
注意:使用vant 包,需要把app.json 中 的"style:v2" 这句去掉 不然会出现样式混乱的问题 Vant Weapp组件库的使用 参考官网 vant官网 Vant Weapp 组件样式覆盖 Vant Weapp 基于微信小程序的机制,为开发者提供了 3 种修改组件样式…...
前端弄一个变量实现点击次数在前端页面实时更新)
(接上一篇)前端弄一个变量实现点击次数在前端页面实时更新
实现点击次数在前端页面实时更新,确实需要在前端维护一个变量来存储当前的点击次数。这个变量通常在Vue组件的data选项中定义,并在组件的生命周期方法或事件处理函数中更新。 以下是实现这一功能的基本步骤: 定义变量:在Vue组件的…...

迭代器模式在金融业务中的应用及其框架实现
引言 迭代器模式(Iterator Pattern)是一种行为设计模式,它提供了一种方法顺序访问一个聚合对象中的各个元素,而又不需要暴露该对象的内部表示。在金融业务中,迭代器模式可以用于遍历复杂的数据结构,如交易…...
浏览器插件利器-allWebPluginV2.0.0.14-stable版发布
allWebPlugin简介 allWebPlugin中间件是一款为用户提供安全、可靠、便捷的浏览器插件服务的中间件产品,致力于将浏览器插件重新应用到所有浏览器。它将现有ActiveX插件直接嵌入浏览器,实现插件加载、界面显示、接口调用、事件回调等。支持谷歌、火狐等浏…...

机器学习训练之使用静态图加速
前言 MindSpore有两种运行模式:动态图模式和静态图模式。默认情况下是动态图模式,也可以手工切换为静态图模式。 动态图模式 动态图的特点是计算图的构建和计算同时发生,符合Python的解释执行方式。在调试模型时较为方便,能够实…...
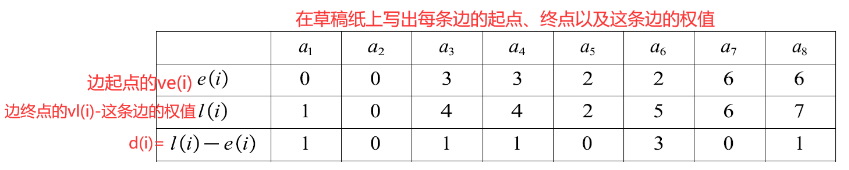
数据结构速成--图
由于是速成专题,因此内容不会十分全面,只会涵盖考试重点,各学校课程要求不同 ,大家可以按照考纲复习,不全面的内容,可以看一下小编主页数据结构初阶的内容,找到对应专题详细学习一下。 目录 …...

昇思25天学习打卡营第12天|FCN图像语义分割
文章目录 昇思MindSpore应用实践基于MindSpore的FCN图像语义分割1、FCN 图像分割简介2、构建 FCN 模型3、数据预处理4、模型训练自定义评价指标 Metrics 5、模型推理结果 Reference 昇思MindSpore应用实践 本系列文章主要用于记录昇思25天学习打卡营的学习心得。 基于MindSpo…...

昇思MindSpore学习笔记4-03生成式--Diffusion扩散模型
摘要: 记录昇思MindSpore AI框架使用DDPM模型给图像数据正向逐步添加噪声,反向逐步去除噪声的工作原理和实际使用方法、步骤。 一、概念 1. 扩散模型Diffusion Models DDPM(denoising diffusion probabilistic model) (无)条件…...

Go:hello world
开启转职->Go开发工程师 下面是我的第一个go的程序 在上面的程序介绍: 1、package main 第一行代码package main定义了包名。必须在源文件中非注释的第一行指明这个文件属于哪个包,如:package main。package main表示一个可独立执行的程…...

JVM专题之内存模型以及如何判定对象已死问题
体验与验证 2.4.5.1 使用visualvm **visualgc插件下载链接 :https://visualvm.github.io/pluginscenters.html https://visualvm.github.io/pluginscenters.html **选择对应JDK版本链接--->Tools--->Visual GC** 2.4.5.2 堆内存溢出 * **代码** java @RestCont…...

vscode使用Git的常用操作
主打一个实用 查看此篇之前请先保证电脑安装了Git,安装教程很多,可自行搜索 一.初始化本地仓库🔴 使用vscode打开项目文件夹如图所使初始化仓库,相当于命令行的git init 二.提交到暂存区🔴 二.提交到新版本…...

RPC与REST
RPC与REST 访问远程服务1远程服务调用(Remote Procedure Call,RPC):RPC 解决什么问题?如何解决的?为什么要那样解决?1.1 先解决两个进程间如何交换数据的问题,也就是进程间通信&…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...
