牛客周赛 Round 50
A题:小红的最小最大
思路:
大水题
code:
inline void solve() {int a, b, c; cin >> a >> b >> c;if (min(a, b) + c > max(a, b)) cout << "YES\n";else cout << "NO\n";return;
}B题:小红的四则运算(easy)
思路:
大水题
code:
inline void solve() {int ans = 0;int a, b, c; cin >> a >> b >> c;int cur = a + b + c;ans = max(ans, cur);cur = a * b + c;ans = max(ans, cur);cur = a + b * c;ans = max(ans, cur);cur = a * b * c;ans = max(ans, cur);cur = a * (b + c);ans = max(ans, cur);cur = (a + b) * c;ans = max(ans, cur);cout << ans << endl;return;
}C题:小红的四则运算(hard)
思路:
大水题
code:
inline void solve() {int ans = 0;int a, b, c; cin >> a >> b >> c;int cur = a + b + c;ans = max(ans, cur);cur = a * b + c;ans = max(ans, cur);cur = a + b * c;ans = max(ans, cur);cur = a * b * c;ans = max(ans, cur);cur = a * (b + c);ans = max(ans, cur);cur = (a + b) * c;ans = max(ans, cur);cout << ans << endl;return;
}D题:小红的因式分解
思路:
十字相乘大法。
注意正的可以表示为两个负的相乘。
code:
inline void solve() {ll a, b, c;cin >> a >> b >> c;if (c == 0) {cout << 1 << ' ' << 0 << ' ' << a << ' ' << b << endl;return;}vector<PLL> l, r;function<void(ll, vector<PLL>&)> add = [&](ll x, vector<PLL>& e) {for (ll i = min(1ll, x); i < max(0ll, x + 1); i ++ ) {if (x % i == 0) {e.push_back({i, x / i});e.push_back({-i, -x / i});}}};add(a, l), add(c, r);bool ok = false;for (auto [l1, l2] : l) {for (auto [r1, r2] : r) {if (l1 * r1 + l2 * r2 == b) {ok = true;cout << l1 << ' ' << r2 << ' ' << l2 << ' ' << r1 << endl;break;}}if (ok) break;}if (!ok) cout << "NO\n";return;
}E题:小红的树上移动
思路:
学过期望和逆元应该就会做了。
期望等于各个值乘以它的概率的和,对于此题,我们只需统计下每层的叶节点数量和节点数量即可。
inline void solve() {mod = 998244353;int n; cin >> n;vector<vector<int>> e(n + 1);for (int i = 1; i < n; i ++ ) {int u, v; cin >> u >> v;e[u].push_back(v), e[v].push_back(u);}vector<int> dep(n + 1), cnt(n + 1), tot(n + 1);function<void(int, int)> dfs = [&](int u, int pre) {dep[u] = dep[pre] + 1;tot[dep[u]] += 1;if (e[u].size() == 1 && u != 1) cnt[dep[u]] += 1;for (auto v : e[u]) {if (v == pre) continue;dfs(v, u);}};dfs(1, 0);ll ans = 0, lv = 1;for (int i = 1; i <= n; i ++ ) {if (cnt[i]) {ll gai = lv * cnt[i] % mod * inv(tot[i]) % mod;ans = (ans + (i - 1) * gai % mod) % mod;lv = lv * (tot[i] - cnt[i]) % mod * inv(tot[i]) % mod;}}cout << ans << endl;return;
}相关文章:

牛客周赛 Round 50
A题:小红的最小最大 思路: 大水题 code: inline void solve() {int a, b, c; cin >> a >> b >> c;if (min(a, b) c > max(a, b)) cout << "YES\n";else cout << "NO\n";return; }…...

后端之路——登录校验
前言:Servlet 【登录校验】这个功能技术的基础是【会话技术】,那么在讲【会话技术】的时候必然要谈到【Cookie】和【Session】这两个东西,那么在这之前必须要先讲一下一个很重要但是很多人都会忽略的一个知识点:【Servlet】 什么是…...
无线网卡怎么连接台式电脑?让上网更便捷!
随着无线网络的普及,越来越多的台式电脑用户希望通过无线网卡连接到互联网。无线网卡为台式电脑提供了无线连接的便利性,避免了有线网络的束缚。本文将详细介绍无线网卡怎么连接台式电脑的四种方法,包括使用USB无线网卡、内置无线网卡以及使用…...

【45 Pandas+Pyecharts | 去哪儿海南旅游攻略数据分析可视化】
文章目录 🏳️🌈 1. 导入模块🏳️🌈 2. Pandas数据处理2.1 读取数据2.2 查看数据信息2.3 日期处理,提取年份、月份2.4 经费处理2.5 天数处理 🏳️🌈 3. Pyecharts数据可视化3.1 出发日期_…...

Vue3项目给ElementPlus设置中文的两个方案
介绍 在Vue3项目将ElementPlus切换为中文 1、在App.vue的文件中修改 <template><el-config-provider :locale"zhCn"><router-view></router-view></el-config-provider> </template><script lang"ts" setup>im…...

C#开发单实例应用程序并响应后续进程启动参数
C#默认的WinForm模板是不支持设置单实例的,也没有隔壁大哥VB.NET那样有个“生成单个实例应用程序”的勾选选项(VB某些时候要比C#更方便),实现单实例可以有多种方法: 检测同名进程:Process.GetProcessesByNa…...

STM32智能机器人导航系统教程
目录 引言环境准备智能机器人导航系统基础代码实现:实现智能机器人导航系统 4.1 数据采集模块 4.2 数据处理与导航算法 4.3 通信与网络系统实现 4.4 用户界面与数据可视化应用场景:机器人导航应用与优化问题解决方案与优化收尾与总结 1. 引言 智能机器…...
Android 15 适配之16K Page Size :为什么它会是最坑的一个适配点
首先什么是 Page Size ?一般意义上,页面(Page)指的就是 Linux 虚拟内存管理中使用的最小数据单位,页面大小(Page Size)就是虚拟地址空间中的页面大小, Linux 中进程的虚拟地址空间是由固定大小的页面组成。 Page Size 对于虚拟内…...

下载linux的吐槽
本来这几天放假了,想下一个linux玩一玩 教程(我就是根据这个教程进行下载的,但是呢在进行修改BIOS 模式的 地方遇见了困难,也许是电脑修过的原因,我狂按F12 以及 FnF12都没有BIOS设置,只有一个让我选择用w…...

【HTML入门】第四课 - 换行、分割横线和html的注释
这一小节,我们继续说HTML的入门知识,包括换行、横线分割以及注释(html的注释)。 目录 1 换行 2 分割横线 3 html注释 1 换行 html中分为块元素和行内元素。这一小节呢,先不说这些元素们,我们先说一下换…...
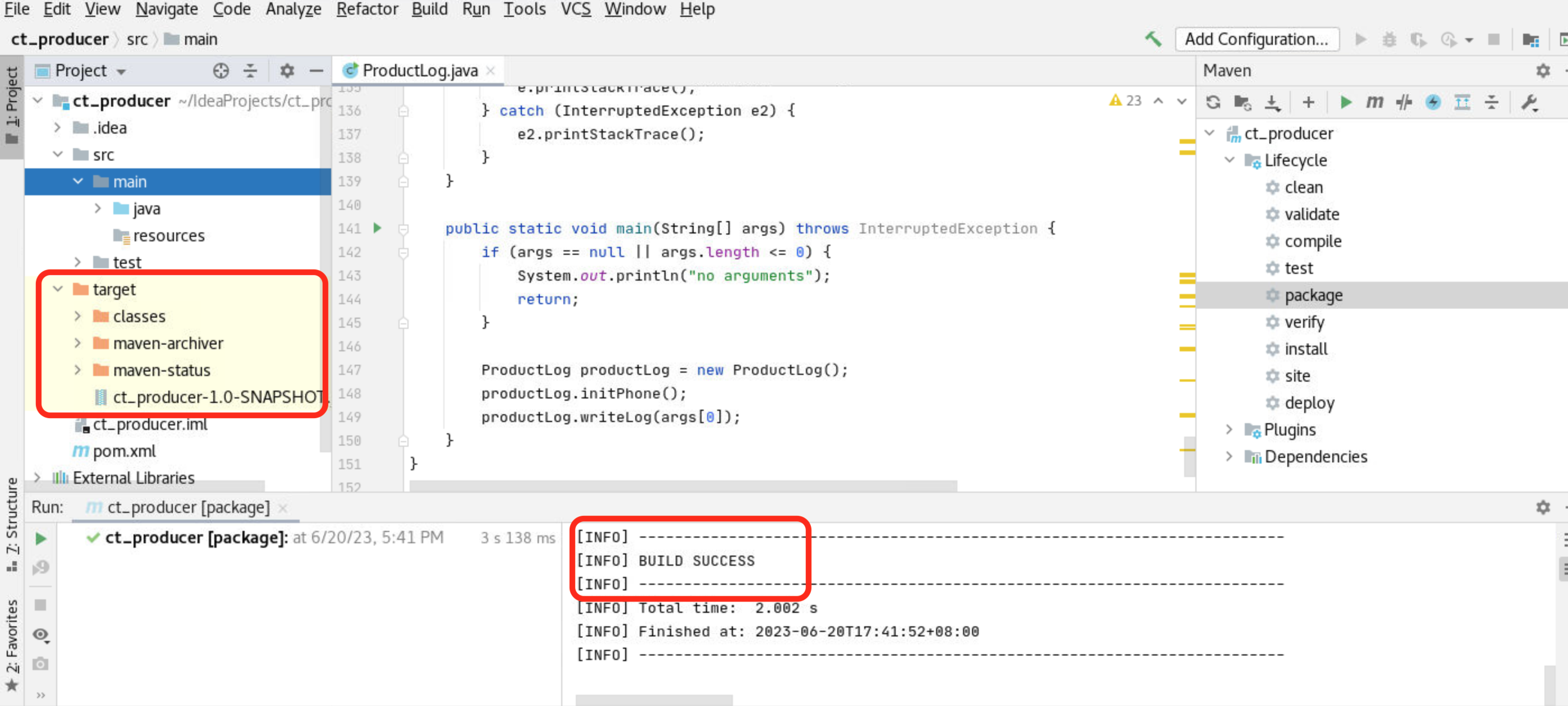
基于Hadoop平台的电信客服数据的处理与分析④项目实现:任务15:数据生产
任务描述 电信数据生产是一个完整且严密的体系,这样可以保证数据的鲁棒性。在本项目的数据生产模块中,我们来模拟生产一些电信数据。同时,我们必须清楚电信数据的格式和数据结构,这样才能在后续的数据产生、存储、分析和展示环节…...

Kotlin中的数据类型
人不走空 🌈个人主页:人不走空 💖系列专栏:算法专题 ⏰诗词歌赋:斯是陋室,惟吾德馨 目录 🌈个人主页:人不走空 💖系列专栏:算法专题 ⏰诗词歌…...

提高交易决策质量,Anzo Capital昂首资本只需两个交易策略
要想提高交易决策质量,其实很简单,Anzo Capital昂首资本只需两个交易策略,结合价格行为和VSA(成交量与价格分析)就可以达成我们的目的。首先,理解这两个概念: 1. 价格行为:价格行为是市场价格变动的方式&a…...
Ubuntu TensorRT安装
什么是TensorRT 一般的深度学习项目,训练时为了加快速度,会使用多 GPU 分布式训练。但在部署推理时,为了降低成本,往往使用单个 GPU 机器甚至嵌入式平台(比如 NVIDIA Jetson)进行部署,部署端也…...

spring mvc学习
第四章 Spring MVC 第一节 Spring MVC 简介 1. Spring MVC SpringMVC是一个Java 开源框架, 是Spring Framework生态中的一个独立模块,它基于 Spring 实现了Web MVC(数据、业务与展现)设计模式的请求驱动类型的轻量级Web框架&am…...

第4集《修习止观坐禅法要》
请打开讲义第七面,四、悟道。 我们前面讲到智者大师出家以后,他除了持戒以外,一方面拜忏,一方面就是打坐,来调伏他过去的烦恼跟罪业,以为他未来圆顿止观的一个基础,这以下讲到他开悟的情况&…...

IPython 日志的开关:精通 %logoff 命令的实用指南
IPython 日志的开关:精通 %logoff 命令的实用指南 在 IPython 的强大功能中,日志记录是一个不可或缺的工具,它帮助用户记录会话历史,以便日后分析和重现。%logoff 命令作为日志记录功能的补充,允许用户在需要时停止日…...

Redis 分布式集群方案 Cluster
引言 相比于Codis,Redis Cluster是Redis官方提供的解决方案。相比于Codis的不同,他是去中心化的,如图所示,该集群有三个Redis节点组成,每个节点负责整个集群的一部分数据,每个节点负责的数据多少可能不一样…...

Redis的两种持久化方案
Redis 提供了多种持久化机制来保证数据在发生意外情况下(如断电或服务器崩溃)不丢失。以下是几种主要的 Redis 持久化方案及其特点: 1. RDB (Redis Database Backup) RDB 是 Redis 创建的数据库快照,它可以将数据集快照以二进制…...

Spring中常见知识点及使用
Spring Framework 是 Java 生态系统中最流行的开源框架之一,它提供了一系列强大的功能,用于构建企业级应用。以下是一些常见的 Spring 知识点及其使用方法: 1. 依赖注入(Dependency Injection) 依赖注入是 Spring 的…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

探索Selenium:自动化测试的神奇钥匙
目录 一、Selenium 是什么1.1 定义与概念1.2 发展历程1.3 功能概述 二、Selenium 工作原理剖析2.1 架构组成2.2 工作流程2.3 通信机制 三、Selenium 的优势3.1 跨浏览器与平台支持3.2 丰富的语言支持3.3 强大的社区支持 四、Selenium 的应用场景4.1 Web 应用自动化测试4.2 数据…...

Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...

python爬虫——气象数据爬取
一、导入库与全局配置 python 运行 import json import datetime import time import requests from sqlalchemy import create_engine import csv import pandas as pd作用: 引入数据解析、网络请求、时间处理、数据库操作等所需库。requests:发送 …...

2025年低延迟业务DDoS防护全攻略:高可用架构与实战方案
一、延迟敏感行业面临的DDoS攻击新挑战 2025年,金融交易、实时竞技游戏、工业物联网等低延迟业务成为DDoS攻击的首要目标。攻击呈现三大特征: AI驱动的自适应攻击:攻击流量模拟真实用户行为,差异率低至0.5%,传统规则引…...

聚六亚甲基单胍盐酸盐市场深度解析:现状、挑战与机遇
根据 QYResearch 发布的市场报告显示,全球市场规模预计在 2031 年达到 9848 万美元,2025 - 2031 年期间年复合增长率(CAGR)为 3.7%。在竞争格局上,市场集中度较高,2024 年全球前十强厂商占据约 74.0% 的市场…...

Vue 实例的数据对象详解
Vue 实例的数据对象详解 在 Vue 中,数据对象是响应式系统的核心,也是组件状态的载体。理解数据对象的原理和使用方式是成为 Vue 专家的关键一步。我将从多个维度深入剖析 Vue 实例的数据对象。 一、数据对象的定义方式 1. Options API 中的定义 在 Options API 中,使用 …...

vxe-table vue 表格复选框多选数据,实现快捷键 Shift 批量选择功能
vxe-table vue 表格复选框多选数据,实现快捷键 Shift 批量选择功能 查看官网:https://vxetable.cn 效果 代码 通过 checkbox-config.isShift 启用批量选中,启用后按住快捷键和鼠标批量选取 <template><div><vxe-grid v-bind"gri…...
