0/1背包问题总结
文章目录
- 🍇什么是0/1背包问题?
- 🍈例题
- 🍉1.分割等和子集
- 🍉2.目标和
- 🍉3.最后一块石头的重量Ⅱ
- 🍊总结

博客主页:lyyyyrics
🍇什么是0/1背包问题?
0/1背包问题是一个经典的组合优化问题,其描述如下:
假设有一个背包,它能够承载一定的重量。现在有一组物品,每个物品有各自的重量和价值。我们的目标是在不超过背包承载重量的前提下,选择一些物品放入背包中,使得背包中物品的总价值最大化。
具体来说,假设有 n n n个物品,其重量分别为 w 1 , w 2 , . . . , w n w_1, w_2, ..., w_n w1,w2,...,wn,对应的价值分别为 v 1 , v 2 , . . . , v n v_1, v_2, ..., v_n v1,v2,...,vn。背包的承载重量为 W W W。我们需要在这 n n n个物品中选择一些放入背包中,使得这些物品的总重量不超过 W W W,且总价值最大化。
数学公式可以表示为:
Maximize ∑ i = 1 n v i x i subject to ∑ i = 1 n w i x i ≤ W x i ∈ { 0 , 1 } , i = 1 , 2 , . . . , n \begin{align*} \text{Maximize} \quad & \sum_{i=1}^{n} v_ix_i \\ \text{subject to} \quad & \sum_{i=1}^{n} w_ix_i \leq W \\ & x_i \in \{0, 1\}, \quad i=1,2,...,n \end{align*} Maximizesubject toi=1∑nvixii=1∑nwixi≤Wxi∈{0,1},i=1,2,...,n
其中, x i x_i xi表示第 i i i个物品是否放入背包中。若 x i = 1 x_i=1 xi=1,表示放入;若 x i = 0 x_i=0 xi=0,表示不放入。
🍈例题
🍉1.分割等和子集
题目:
样例输出和输入:
根据描述,这道题就是让我们求一个数组是否能将其分成两块 ,然后这两块是相等的,如果能返回true,如果不能则返回false。
算法原理:
首先我们注意到,这道题要将数组分成两个部分,这两个部分是否相等,我们可以转化为分成一个部分,这个部分是数组总和的一半?很显然是可以的,这样转换之后其实就已经是背包问题了,这个数组中的数就是物品,数组中的数就代表每个物品的价值,然后数组中的数的总和的一半就是这个背包的容量,问题就 转化为,我们是否可以从数组中挑出一些物品,使得物品的体积恰好能把这个 背包塞满?
状态表示:dp[i][j]表示前i个数中的所有的选法中,是否存在和为j的选法,如果存在则是true,如果不存在则就是false。
状态转移方程:状态转移方程还是考虑i位置和j位置。

如果能选的话,应该是选和不选中有一个满足就够了,所以这里应该还要取一个||,dp[i][j]=dp[i-1][j]||dp[i-1][j-nums[i]]
初始化:
首先看第一行,从1开始,从0个数中选,和为1的,这种情况是不存在的,所以应该是false,后面的从0个数中选的都是false,,我们来看第一列,从0个数中选和为0,那就是不选,所以为true,从1个数中选和为0,可以不选,也是true,所以我们只需要 初始化第一列,初始化为true。
代码:
class Solution {
public:bool canPartition(vector<int>& nums){int n = nums.size();int sum = 0;//求和for (auto e : nums)sum += e;//如果和是奇数的话直接返回if (sum % 2 == 1)return false;//先定义一个aim表示和的一半int aim = sum / 2;//创建dp表vector<vector<bool>> dp(n + 1, vector<bool>(aim + 1));//初始化dp表的第一列为true,因为如果和为零的话是有可能的。//如果什么都不选的话,当前和就是0for (int i = 0;i <= n;i++){dp[i][0] = true;}for (int i = 1;i <= n;i++){for (int j = 1;j <= aim;j++){//不选的话就是前一个状态的bool值dp[i][j] = dp[i - 1][j];//如果能选的话,只要有一种满足就表示满足if (j >= nums[i - 1])dp[i][j] = dp[i - 1][j] || dp[i - 1][j - nums[i - 1]];}}//返回和为aim的状态return dp[n][aim];}
};
运行结果:

🍉2.目标和
题目:
样例输出和输入:
这道题是给定一个数组,我们可以将数组中数 的符号我们可以随便改,最后串成一个加减法的式子,然后这个式子的值为target即可,这道题当然不是让我们返回true或者false,而是让我们返回方法的总数。
算法原理:
这道题其实我们可以将当中的数划分为两类:

我们将b规定为负数的绝对值。
所以最后可以得出:
所以我们只需要看这个数组中是否组合能使得这个组合最后的和是a即可。
状态表示:dp[i][j]表示从前i个数中选,所有选法中和为j的方法。
状态转移方程:状态转移方程还是看第i个位置:

如果能选的话,则方法总数就是选和不选的和:dp[i][j]+=dp[i-1][j-nums[i]],但是有一个条件:j>nums[i]。
代码:
class Solution
{
public:int findTargetSumWays(vector<int>& nums, int target){int n = nums.size();int sum = 0;for (auto e : nums)sum += e;int aim = (sum + target) / 2;if (aim < 0 || (sum + target) % 2 == 1)return 0;vector<vector<int>> dp(n + 1, vector<int>(aim + 1));dp[0][0] = 1;for (int i = 1;i <= n;i++){for (int j = 0;j <= aim;j++){dp[i][j] = dp[i - 1][j];if (j >= nums[i - 1])dp[i][j] += dp[i - 1][j - nums[i - 1]];}}return dp[n][aim];}
};
运行结果:

🍉3.最后一块石头的重量Ⅱ
题目:
这道题的题目是“最后一块石头的重量 II”。
样例输出和输入:
给定一堆石头的重量数组stones,在每一回合中,选出两块石头粉碎,最后剩下的石头的重量可能为:
- 如果选出的两块石头重量相等,那么两块石头都会被完全粉碎;
- 如果选出的两块石头重量不相等,重量为较小的石头将会完全粉碎,而重量为较大的石头新重量为较大石头的重量减去较小石头的重量。
问题要求找到最后剩下的石头的最小可能重量。如果没有剩下的石头,返回0。给定一堆石头的重量数组stones,在每一回合中,选出两块石头粉碎,最后剩下的石头的重量可能为:
- 如果选出的两块石头重量相等,那么两块石头都会被完全粉碎;
- 如果选出的两块石头重量不相等,重量为较小的石头将会完全粉碎,而重量为较大的石头新重量为较大石头的重量减去较小石头的重量。
问题要求找到最后剩下的石头的最小可能重量。如果没有剩下的石头,返回0。
算法原理:
首先我们模拟一遍这个过程:

注意:上述过程是建立在前一个比后一个大的基础上模拟的
我们可以发现:当中的数也是有正有负,相当与也可以分成两个分类,一个正一个负:


其实我们不难看出,当a和b最接近的时候,这时候差值最小,所以这道题我们就可以转换成了0/1背包问题:
相当于a和b都接近于sum/2,所以这道题的背包容量是sum/2,
状态表示:dp[i][j]表示前i个物品中选,总和不超过j的,最大的和。
状态转移方程:
当存在第一种情况的是否需要和不选的情况求一个最大值:dp[i][j]=max(dp[i-1][j],dp[i-1][j-stones[i]]+stones[i]
代码:
int lastStoneWeightII(vector<int>& stones)
{int n = stones.size();int sum = 0;for (auto e : stones)sum += e;vector<vector<int>> dp(n + 1, vector<int>(sum / 2 + 1));for (int i = 1;i <= n;i++){for (int j = 1;j <= sum / 2;j++){dp[i][j] = dp[i - 1][j];if (j >= stones[i - 1])dp[i][j] = max(dp[i - 1][j - stones[i - 1]] + stones[i - 1], dp[i - 1][j]);}}int a = dp[n][sum / 2];int b = sum - a;return abs(a - b);
}
空间优化过的代码:二维---->一维
class Solution {
public:int lastStoneWeightII(vector<int>& stones){int n = stones.size();int sum = 0;for (auto e : stones)sum += e;vector<int> dp(sum / 2 + 1);for (int i = 1;i <= n;i++)for (int j = sum / 2;j >= stones[i - 1];j--)dp[j] = max(dp[j - stones[i - 1]] + stones[i - 1], dp[j]);int a = dp[sum / 2];int b = sum - a;return abs(a - b);}
};
运行结果:

🍊总结
0/1 背包问题是组合优化中的经典问题,通过研究和解决这一问题,可以深入理解动态规划的基本思想和应用。本文详细介绍了0/1背包问题的定义、数学模型及其动态规划解法,并通过C++代码示例展示了具体的实现步骤。
通过本次总结,希望读者能够掌握如何将理论知识应用于实际问题,理解状态转移方程的推导过程,以及如何优化算法以提升效率。背包问题不仅在学术研究中具有重要意义,还广泛应用于资源分配、项目管理等实际领域。掌握这一问题的解决方法,可以为解决更复杂的优化问题打下坚实的基础。
在今后的学习中,建议读者多多练习不同变种的背包问题,如完全背包、多重背包问题等,以进一步提升自己的算法设计和分析能力。感谢阅读,希望本文对你的学习和应用有所帮助。
相关文章:

0/1背包问题总结
文章目录 🍇什么是0/1背包问题?🍈例题🍉1.分割等和子集🍉2.目标和🍉3.最后一块石头的重量Ⅱ 🍊总结 博客主页:lyyyyrics 🍇什么是0/1背包问题? 0/1背包问题是…...

模电基础 - 放大电路的频率响应
目录 一. 简介 二. 频率响应的基本概念 三. 波特图 四. 晶体管的高频等效模型 五. 场效应管的高频等效模型 六. 单管放大电路的频率响应 七.多级放大电路的频率响应 八. 频率响应与阶跃响应 一. 简介 放大电路的频率响应是指在输入不同频率的正弦信号时,电路…...

Java 8 到 Java 22 新特性详解
Java 8 到 Java 22 新特性详解 Java自发布以来一直在不断演进,添加新特性以提升开发效率和性能。本文将介绍Java 8到Java 22的主要新特性,帮助开发者了解各版本的新功能和改进。 Java 8 (2014) 1. Lambda 表达式 Lambda 表达式允许使用简洁的语法定义…...

华为OD机试题-提取字符串中最长数学表达式
题目描述 https://blog.csdn.net/weixin_51055612/article/details/139841128 题目描述 提取字符串中的最长合法简单数学表达式,字符串长度最长的,并计算表达式的值。如果没有,则返回0。 简单数学表达式只能包含以下内容:0-9数字&…...

专家指南:如何为您的电路选择理想的压敏电阻或热敏电阻
保护和维持电路功能需要两种设备:压敏电阻和热敏电阻。这两个电气元件有时会因后缀相似而混淆,但它们具有不同且重要的用途。 由于这种混淆,我们需要准确地了解这些组件是什么,这就是本文将要讨论的内容——应用程序、作用、优点…...
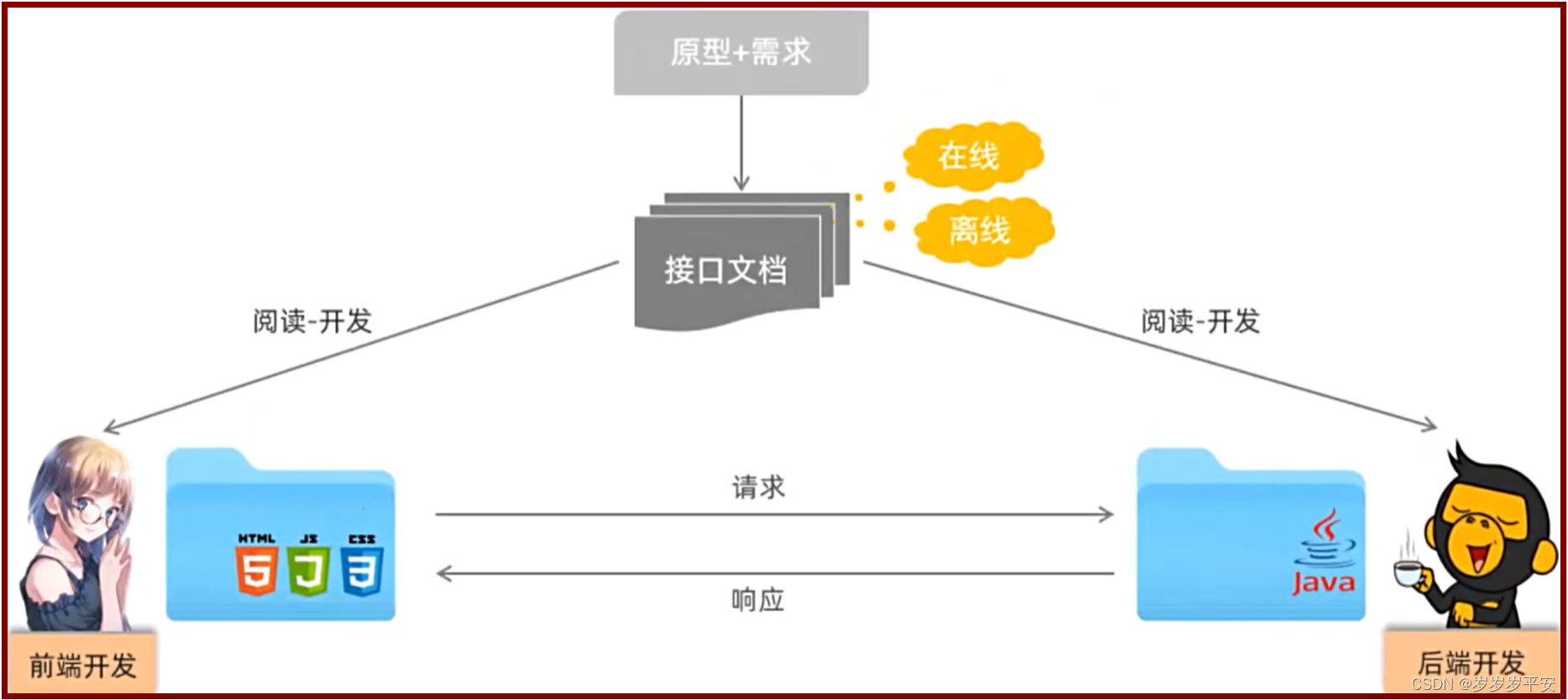
基于主流SpringBoot进行JavaWeb开发的学习路线
目录 一、学习路线 (1)第一部分(Web前端开发的技术栈) (2)第二部分(Web后端开发) 二、学习之后必备的技能 三、学习Web开发的基础与未来的收获 学完这一类知识目标:…...

医疗机器人中的具身智能进展——自主超声策略模型的任务编码和局部探索
医疗机器人一直是具身智能的研究热点。医学图像、医疗触诊、血压血氧、心率脉搏和生物电信号等多模态生物医学信息,不断丰富着医疗机器人的感知范畴。 自主超声 “自主超声”属于具身智能医疗机器人领域中话题度较高的研究方向。作为临床检查的重要手段之一&#…...

探索人工智能在电子商务平台与游戏发行商竞争中几种应用方式
过去 12 年来,电脑和视频游戏的发行策略发生了巨大变化。数字游戏的销量首次超过实体游戏的销量 在20132020 年的封锁进一步加速了这一趋势。例如,在意大利,封锁的第一周导致数字游戏下载量 暴涨174.9%. 展望未来,市场有望继续增…...

【Altium】AD-网络版一个用户非人为异常占用多个License的解决方法
【更多软件使用问题请点击亿道电子官方网站】 1、 文档目标 当出现一个用户同时占用多个授权,又无法单独释放一个授权的情况下,该如何解决。 2、 问题场景 一个用户获取网络版授权后,AD会自动重复获取授权,直到该license下所有授…...
第二十五天 | 134. 加油站、135. 分发糖果、860. 柠檬水找零、406. 根据身高重建队列)
*算法训练(leetcode)第二十五天 | 134. 加油站、135. 分发糖果、860. 柠檬水找零、406. 根据身高重建队列
刷题记录 134. 加油站135. 分发糖果860. 柠檬水找零406. 根据身高重建队列 134. 加油站 leetcode题目地址 记录全局剩余油量和当前剩余油量,当前剩余小于0时,其实位置是当前位置的后一个位置。若全局剩余油量为负,则说明整体油量不足以走完…...

乐鑫ESPC3 ESP8685 WiFi蓝牙模块透传程序设置教程,抛开繁琐AT指令,简单Web页面配置,即可实现透传
完整文档请下载规格书 TTL-WiFi 透传产品 使用手册 一. 产品概述 二. 接口定义 三. 软件透传WEB配置使用说明 3.1 STATUS配置界面 3.2 MODULE配置界面 n Serial(串口配置) n WiFi(WiFi配置) n Networks(网络…...

怎么样才能为公司申请OV证书?
OV证书,全称为组织验证型SSL证书(Organization Validation SSL Certificate),是一种高级别的SSL/TLS证书,用于加密网站通信并验证网站所属组织的合法身份。相比于基本的域名验证型证书(DV证书)&…...

Python的`queue`模块
队列(Queue) 在Python的queue模块中,Queue类是一个线程安全的队列实现,用于在多线程编程中安全地交换信息。它遵循先入先出(FIFO)的原则。Queue类提供了几种主要的方法: put(item): 将一个项目…...

牛客周赛 Round 50
A题:小红的最小最大 思路: 大水题 code: inline void solve() {int a, b, c; cin >> a >> b >> c;if (min(a, b) c > max(a, b)) cout << "YES\n";else cout << "NO\n";return; }…...

后端之路——登录校验
前言:Servlet 【登录校验】这个功能技术的基础是【会话技术】,那么在讲【会话技术】的时候必然要谈到【Cookie】和【Session】这两个东西,那么在这之前必须要先讲一下一个很重要但是很多人都会忽略的一个知识点:【Servlet】 什么是…...
无线网卡怎么连接台式电脑?让上网更便捷!
随着无线网络的普及,越来越多的台式电脑用户希望通过无线网卡连接到互联网。无线网卡为台式电脑提供了无线连接的便利性,避免了有线网络的束缚。本文将详细介绍无线网卡怎么连接台式电脑的四种方法,包括使用USB无线网卡、内置无线网卡以及使用…...

【45 Pandas+Pyecharts | 去哪儿海南旅游攻略数据分析可视化】
文章目录 🏳️🌈 1. 导入模块🏳️🌈 2. Pandas数据处理2.1 读取数据2.2 查看数据信息2.3 日期处理,提取年份、月份2.4 经费处理2.5 天数处理 🏳️🌈 3. Pyecharts数据可视化3.1 出发日期_…...

Vue3项目给ElementPlus设置中文的两个方案
介绍 在Vue3项目将ElementPlus切换为中文 1、在App.vue的文件中修改 <template><el-config-provider :locale"zhCn"><router-view></router-view></el-config-provider> </template><script lang"ts" setup>im…...

C#开发单实例应用程序并响应后续进程启动参数
C#默认的WinForm模板是不支持设置单实例的,也没有隔壁大哥VB.NET那样有个“生成单个实例应用程序”的勾选选项(VB某些时候要比C#更方便),实现单实例可以有多种方法: 检测同名进程:Process.GetProcessesByNa…...

STM32智能机器人导航系统教程
目录 引言环境准备智能机器人导航系统基础代码实现:实现智能机器人导航系统 4.1 数据采集模块 4.2 数据处理与导航算法 4.3 通信与网络系统实现 4.4 用户界面与数据可视化应用场景:机器人导航应用与优化问题解决方案与优化收尾与总结 1. 引言 智能机器…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...

JS手写代码篇----使用Promise封装AJAX请求
15、使用Promise封装AJAX请求 promise就有reject和resolve了,就不必写成功和失败的回调函数了 const BASEURL ./手写ajax/test.jsonfunction promiseAjax() {return new Promise((resolve, reject) > {const xhr new XMLHttpRequest();xhr.open("get&quo…...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...

ubuntu22.04有线网络无法连接,图标也没了
今天突然无法有线网络无法连接任何设备,并且图标都没了 错误案例 往上一顿搜索,试了很多博客都不行,比如 Ubuntu22.04右上角网络图标消失 最后解决的办法 下载网卡驱动,重新安装 操作步骤 查看自己网卡的型号 lspci | gre…...

ubuntu系统文件误删(/lib/x86_64-linux-gnu/libc.so.6)修复方案 [成功解决]
报错信息:libc.so.6: cannot open shared object file: No such file or directory: #ls, ln, sudo...命令都不能用 error while loading shared libraries: libc.so.6: cannot open shared object file: No such file or directory重启后报错信息&…...

从实验室到产业:IndexTTS 在六大核心场景的落地实践
一、内容创作:重构数字内容生产范式 在短视频创作领域,IndexTTS 的语音克隆技术彻底改变了配音流程。B 站 UP 主通过 5 秒参考音频即可克隆出郭老师音色,生成的 “各位吴彦祖们大家好” 语音相似度达 97%,单条视频播放量突破百万…...






