数据结构——二叉树之c语言实现堆与堆排序
目录
前言:
1.二叉树的概念及结构
1.1 特殊的二叉树
1.2 二叉树的存储结构
1.顺序存储
2.链式存储
2. 二叉树的顺序结构及实现
2.1 堆的概念
编辑
2.2 堆的创建
3.堆的实现
3.1 堆的初始化和销毁
初始化:
销毁:
插入:
向上调整:
删除:
向下调整:
堆顶元素:
判空:
4.堆排序
4.1排序实现
前言:
在上一期我们介绍了有关于树的基础概念,了解了关于树的各名称的含义,然而在现实中树被用得最多的场景还是在我们计算机中的资源管理器的文件存储结构中,在其他场景被使用的情况很少,所以我们这一期要介绍一种被广泛使用的树型结构——二叉树。
1.二叉树的概念及结构
顾名思义,二叉树是由一个根结点和两棵子树构成,二叉树的每个结点最多只有两个结点:

从上图可以看出:
1. 二叉树不存在度大于2的结点
2. 二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树
二叉树是由以下几种情况复合而成的:

现实中的二叉树:
1.1 特殊的二叉树
1. 满二叉树:一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。也就是说,如果一个二叉树的层数为K,且结点总数K次方-1,则它就是满二叉树。
2. 完全二叉树:完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K 的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。

1.2 二叉树的存储结构
二叉树一般可以使用两种结构存储,一种顺序结构,一种链式结构。
1.顺序存储
顺序结构存储就是使用数组来存储,一般使用数组只适合表示完全二叉树,因为不是完全二叉树会有空间的浪费。而现实中使用中只有堆才会使用数组来存储,关于堆我们后面的章节会专门讲解。二叉树顺 序存储在物理上是一个数组,在逻辑上是一颗二叉树。

2.链式存储
二叉树的链式存储结构是指,用链表来表示一棵二叉树,即用链来指示元素的逻辑关系。 通常的方法是 链表中每个结点由三个域组成,数据域和左右指针域,左右指针分别用来给出该结点左孩子和右孩子所 在的链结点的存储地址 。链式结构又分为二叉链和三叉链,当前我们学习中一般都是二叉链,后面课程 学到高阶数据结构如红黑树等会用到三叉链。


2. 二叉树的顺序结构及实现
普通的二叉树是不适合用数组来存储的,因为可能会存在大量的空间浪费。而完全二叉树更适合使用顺序结 构存储。现实中我们通常把堆(一种二叉树)使用顺序结构的数组来存储,需要注意的是这里的堆和操作系统虚拟进程地址空间中的堆是两回事,一个是数据结构,一个是操作系统中管理内存的一块区域分段。

2.1 堆的概念
堆的性质:
1.堆中某个结点的值总是不大于或不小于其父结点的值。
2.堆总是一棵完全二叉树。


2.2 堆的创建
下面我们给出一个数组,这个数组逻辑上可以看做一颗完全二叉树,但是还不是一个堆,现在我们通过算 法,把它构建成一个堆。根结点左右子树不是堆,我们怎么调整呢?这里我们从倒数的第一个非叶子结点的子树开始调整,一直调整到根结点的树,就可以调整成堆。
3.堆的实现
介绍完堆的概念和性质之后,我们接下来就要来用代码实现堆及堆的各个方法。由于堆是顺序结构实现的,所以我们选择使用顺序表来实现它:
typedef int HPDataType;
typedef struct Heap
{HPDataType* a;int size;int capacity;
}HP;3.1 堆的初始化和销毁
堆是用顺序表来实现的,而顺序表的空间都是我们手动在内存中的堆中开辟的,所以也需要手动释放,而在程序最初运行时我们也要对它进行初始化。
初始化:
void HPInit(HP* php)
{assert(php);php->a = NULL;php->size = php->capacity = 0;
}//初始化销毁:
void HPDestroy(HP* php)
{assert(php);free(php->a);php->a = NULL;php->capacity = php->size = 0;
}//销毁插入:
在插入数据之前,我们选确定空间够不够,如果city等于cpapcity,我们就判断空间满了,需要扩容,然后插入数据,而要实现建堆的话,我们还需要使用向上调整方法实现:
void HPPush(HP* php, HPDataType x)
{assert(php);if (php->capacity == php->size){int newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * newcapacity);if (tmp == NULL){perror("realloc fail!");}php->a = tmp;php->capacity = newcapacity;}php->a[php->size] = x;php->size++;AdjustUp(php->a, php->size-1);//向上调整
}//插入向上调整:
向上调整是建堆的关键,在我们插入一个数据时,我们之前建的堆可能会遭到破坏,这时就需要重新调整建堆,我们插入操作是尾插,用堆来表示的话它就是在堆低,这时我们就要向上调整,如果我们建的是小堆,那么我们就要判断我们插入的结点与它的父结点的大小关系,如果它比它的父结点小的话。那么就要与它的父结点交换位置,走到下一轮,如果它还是小于自己的父节点,那么继续执行交换操作,直到数组变成一个小堆:

代码实现:
void AdjustUp(HPDataType* a, int child)
{int parent = (child - 1) / 2;while (child>0){if (a[child] < a[parent]){swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;;}else{break;}}
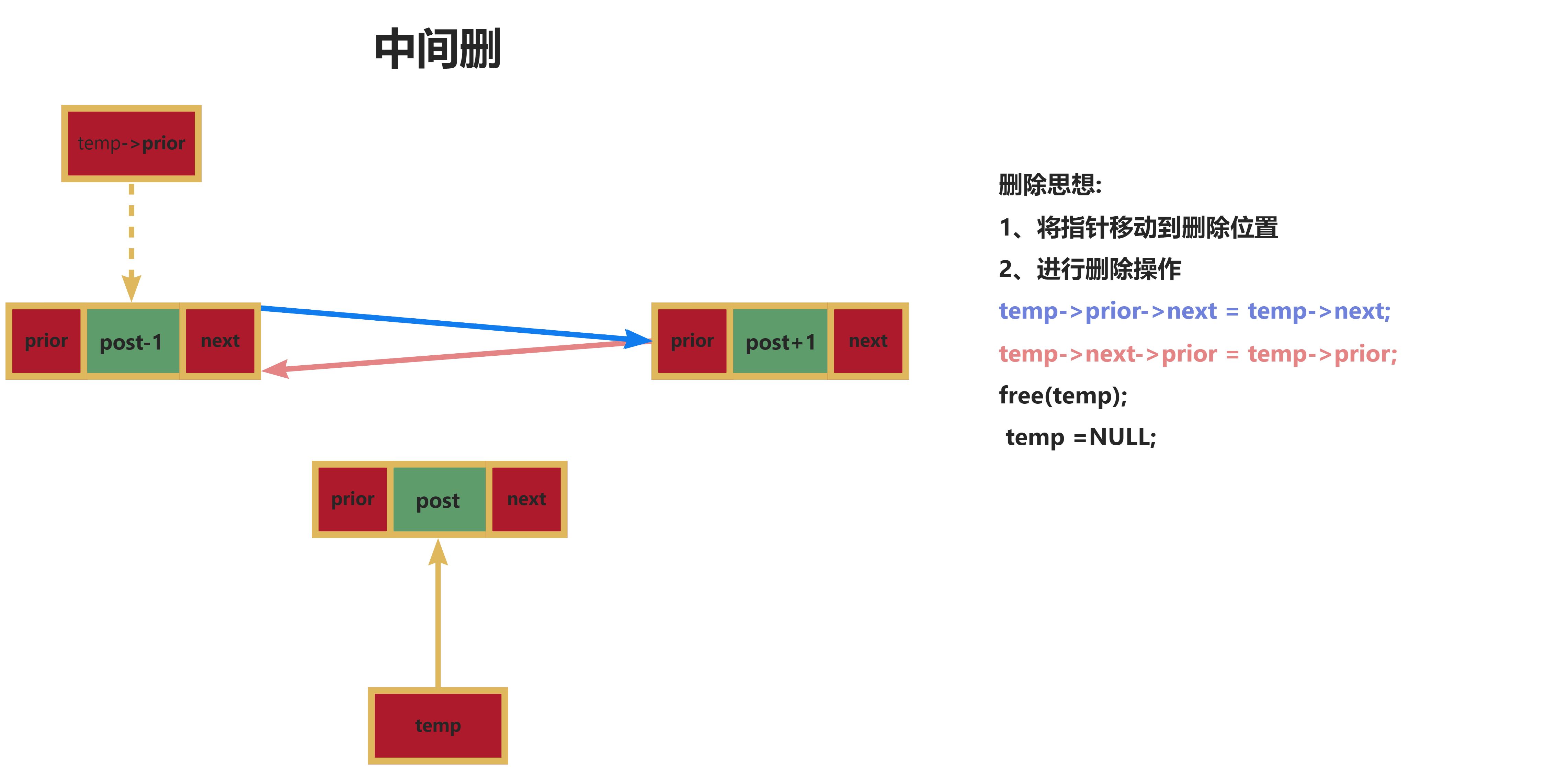
}删除:
有插入操作就必然有删除操作,那么我们如何实现删除操作呢?如果我们直接进行头删,那么我们建的堆就会被破环,如果尾删的话,那么堆就没有意义了(后面详细解释),所以我们先让堆中第一个元素与最后一个元素交换,然后再让size减一,而这时我们建的堆被破环了,所以还需要使用向下调整方法来重新建堆,而向下建堆的算法也比较简单,先找出第一个结点更小的那个子结点,只要这个结点比它的父结点小就让它们交换位置,如此循环往复,直到走到堆尾:

删除代码实现:
void HPPop(HP* php)
{assert(&php);assert(php->size > 0);swap(&(php->a[0]), &(php->a[php->size - 1]));php->size--;AdjustDown(php->a,php->size,0);//向下调整
}//删除向下调整:
void AdjustDown(HPDataType* a, int n, int parent)
{//假设更小的孩子是左孩子int child = parent * 2 + 1;while (child<n)//child>=n说明孩子已经不存在{if (child+1<n&&a[child + 1] < a[child]){child++;}if (a[child] < a[parent]){swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}}//向下调整堆顶元素:
HPDataType HPTop(HP* php)
{assert(php);assert(php->size > 0);return php->a[0];
}//堆顶元素判空:
bool HPEmpty(HP* php)
{assert(php);return php->size = 0;
}//判空
4.堆排序
堆排序是一种速度很快的排序算法,冒泡排序的时间复杂度为O(N^2),而堆排序的时间复杂度仅为O(logN),学完堆,我们就可以来试着实现堆排序了。
4.1排序实现
我们先创建一个无序数组:
int a[] = { 8,6,5,3,9,0,7,1,4,2 };现在这个数组不是堆,我们堆排序的第一步就是先建堆呢,可以使用向下调整吗,答案是不可以,只有下面的子树都是堆时才可以使用,而现在这棵树仅是一个无序数组,所以我们选择从后往前建堆,什么意思呢,我们可以把这组树看成一棵一棵树:

我们发现,从9开始,往上每一个结点都有自己的子结点,这就意味着从就开始,每往前走一步就是一棵树,所以我们只要从9开始使用向下调整建堆,每往前走一步就可以实现一棵树的建堆,而走到8时,整棵树也就完成了建堆:
int a[] = { 8,6,5,3,9,0,7,1,4,2 };
int len = sizeof(a) / sizeof(int);
for (int i = (len - 1 - 1) / 2; i >= 0; i--)
{AdjustDown(a, len, i);
}//建堆这个算法到底怎么样呢?我们运行一下程序看看:

我们将这些数字摆成一棵二叉树:

从上图可以看出,这组数字摆成一棵二叉树它就是一个标准的堆。
成功建堆之后,我们就可以来使用堆来排序了,从上图可以看出,我们建的是小堆,如果我们要实现降序,可以使用小堆实现吗?答案是可以,而且经过实验,我们得出结论:升序:建大堆 ,降序:建小堆,所以我们使用小堆来实现降序是没有问题的。如何实现呢,我们可以先创建一个变量end指向最后一个结点,然后让第一个结点和尾结点交换,因为第一个结点是整个堆最小的数,交换位置之后,最小的数就在最后一个结点了,我们让end向前走一步,然后使用向下调整让堆第二小的数字走到第一个结点,然后再和end指向的结点交换,循环往复之后最大的数就走到了第一个结点,而我们也完成了降序排序:
while (end > 0){swap(&a[0], &a[end]);end--;AdjustDown(a, end, 0);}//调整来看看结果:

下面是完整代码:
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
void swap(int* p1, int* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}
void AdjustDown(int* a, int n, int parent)
{int child = parent * 2 + 1;while (child<n){if (child+1<n&&a[child + 1] < a[child]){child++;}if (a[child] < a[parent]){swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}void test()
{int a[] = { 8,6,5,3,9,0,7,1,4,2 };int len = sizeof(a) / sizeof(int);for (int i = (len - 1 - 1) / 2; i >= 0; i--){AdjustDown(a, len, i);}//建堆int end = len - 1;while (end > 0){swap(&a[0], &a[end]);end--;AdjustDown(a, end, 0);}//调整for (int i = 0; i < len; i++){printf("%d ", a[i]);}
}
int main()
{test();return 0;
}到这里我们的堆就结束了,我将代码放在下面,感兴趣的小伙伴可以试试哦。
Heap.h :
#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>typedef int HPDataType;
typedef struct Heap
{HPDataType* a;int size;int capacity;
}HP;void HPInit(HP* php);//初始化
void HPDestroy(HP* php);//销毁
void HPPush(HP* php, HPDataType x);//插入
void HPPop(HP* php);//删除
HPDataType HPTop(HP* php);//堆顶元素
void AdjustUp(HPDataType* a, int child);//向上调整
void AdjustDown(HPDataType* a, int n,int parent);//向下调整
bool HPEmpty(HP* php);//判空
Heap.c :
#define _CRT_SECURE_NO_WARNINGS 1
#include"Heap.h"void HPInit(HP* php)
{assert(php);php->a = NULL;php->size = php->capacity = 0;
}//初始化
void swap(HPDataType* p1, HPDataType* p2)
{HPDataType tmp = *p1;*p1 = *p2;*p2 = tmp;
}//交换
void AdjustDown(HPDataType* a, int n, int parent)
{//假设更小的孩子是左孩子int child = parent * 2 + 1;while (child<n)//child>=n说明孩子已经不存在{if (child+1<n&&a[child + 1] < a[child]){child++;}if (a[child] < a[parent]){swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}}//向下调整
void AdjustUp(HPDataType* a, int child)
{int parent = (child - 1) / 2;while (child>0){if (a[child] < a[parent]){swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;;}else{break;}}
}
//向上调整
void HPPush(HP* php, HPDataType x)
{assert(php);if (php->capacity == php->size){int newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * newcapacity);if (tmp == NULL){perror("realloc fail!");}php->a = tmp;php->capacity = newcapacity;}php->a[php->size] = x;php->size++;AdjustUp(php->a, php->size-1);//向上调整
}//插入
void HPPop(HP* php)
{assert(&php);assert(php->size > 0);swap(&(php->a[0]), &(php->a[php->size - 1]));php->size--;AdjustDown(php->a,php->size,0);//向下调整
}//删除
HPDataType HPTop(HP* php)
{assert(php);assert(php->size > 0);return php->a[0];
}//堆顶元素
bool HPEmpty(HP* php)
{assert(php);return php->size = 0;
}//判空void HPDestroy(HP* php)
{assert(php);free(php->a);php->a = NULL;php->capacity = php->size = 0;
}//销毁test.c :
#define _CRT_SECURE_NO_WARNINGS 1
#include"Heap.h"
void test()
{int a[] = { 4,9,0,2,5,3,7,1,8,6 };HP hp;HPInit(&hp);for (size_t i = 0; i < sizeof(a) / sizeof(int); i++){HPPush(&hp, a[i]);}while (hp.size){printf("%d ", hp.a[hp.size - 1]);hp.size--;}HPDestroy(&hp);
}
void test02()
{int a[] = { 4,9,0,2,5,3,7,1,8,6 };HP hp;HPInit(&hp);for (size_t i = 0; i < sizeof(a) / sizeof(int); i++){HPPush(&hp, a[i]);}while (hp.size>0){int top = HPTop(&hp);printf("%d ", top);HPPop(&hp);}HPDestroy(&hp);}
void test03()
{int a[] = { 4,9,0,2,5,3,7,1,8,6 };size_t len = sizeof(a) / sizeof(int);for (int i = (len - 1 - 1) / 2; i >= 0; i--){AdjustDown(a, len, i);}int end = len - 1;while (end>0){swap(&a[0], &a[end]);AdjustDown(a, end, 0);end--;}for (int i = 0; i < len; i++){printf("%d ", a[i]);}
}
int main()
{//test02();test03();return 0;
}相关文章:

数据结构——二叉树之c语言实现堆与堆排序
目录 前言: 1.二叉树的概念及结构 1.1 特殊的二叉树 1.2 二叉树的存储结构 1.顺序存储 2.链式存储 2. 二叉树的顺序结构及实现 2.1 堆的概念 编辑 2.2 堆的创建 3.堆的实现 3.1 堆的初始化和销毁 初始化: 销毁: 插入&…...
#数据结构 链表
单向链表 1. 概念 单向链表 单向循环链表 双向链表 双向循环链表 解决:长度固定的问题,插入和删除麻烦的问题 1、逻辑结构: 线性结构 2、存储结构: 链式存储 链表就是将 结点 用链串起来的线性表,链就是 结点 中的…...

单片机软件架构连载(4)-结构体
枚举、指针、结构体,我愿称为C语言"三板斧"。 用人话来讲,几乎所有c语言高阶编程,都离不开这这3个知识点的应用。 今天站在实际产品常用的角度,给大家讲一下结构体。 1.结构体概念 结构体可以用来构建更复杂的数据结…...

工厂方法模式在金融业务中的应用及其框架实现
引言 工厂方法模式(Factory Method Pattern)是一种创建型设计模式,它定义了一个创建对象的接口,但由子类决定实例化哪一个类。工厂方法模式使得类的实例化延迟到子类。在金融业务中,工厂方法模式可以用于创建不同类型…...

python库(6):Pygments库
1 Pygments介绍 在软件开发和文档编写中,代码的可读性是至关重要的一环。无论是在博客文章、技术文档还是教程中,通过代码高亮可以使程序代码更加清晰和易于理解。而在Python世界中,Pygments库就是这样一个强大的工具,它能够将各…...
金斗云 HKMP智慧商业软件 任意用户创建漏洞复现
0x01 产品简介 金斗云智慧商业软件是一款功能强大、易于使用的智慧管理系统,通过智能化的管理工具,帮助企业实现高效经营、优化流程、降低成本,并提升客户体验。无论是珠宝门店、4S店还是其他零售、服务行业,金斗云都能提供量身定制的解决方案,助力企业实现数字化转型和智…...

前端JS特效第24集:jquery css3实现瀑布流照片墙特效
jquery css3实现瀑布流照片墙特效,先来看看效果: 部分核心的代码如下(全部代码在文章末尾): <!DOCTYPE html> <html lang"en"> <head> <meta charset"UTF-8" /> <title>jquerycss3实现瀑…...

区块链论文速读A会-ISSTA 2023(2/2)如何检测DeFi协议中的价格操纵漏洞
Conference:ACM SIGSOFT International Symposium on Software Testing and Analysis (ISSTA) CCF level:CCF A Categories:Software Engineering/System Software/Programming Languages Year:2023 第1~5篇区块链文章 请点击此…...
权力之望怎么下载客户端 权力之望一键下载
《权力之望》是一款由NX3 Games开发、Smilegate发行的多人在线动作MMORPG游戏。这款游戏最大的特点是高度的自由度和丰富的角色定制选项。我们在游戏中不仅可以自由更换武器,而且游戏还提供了54种能力和60多种职业选择,让我们可以根据自己的游戏风格和喜…...

Oracle PL/SQL 循环批量执行存储过程
1. 查询存储过程 根据数据字典USER_OBJECTS查询出所有存储过程。 2. 动态拼接字符串(参数等) 根据数据字典USER_ARGUMENTS动态拼接参数。 3. 动态执行 利用EXECUTE IMMEDIATE动态执行无名块。 4. 输出执行信息 利用DBMS_OUTPUT.PUT_LINE输出执行成功与…...

kafka 生产者
生产者 生产者负责创建消息,然后将其投递到Kafka中。 负载均衡 轮询策略。随机策略。按照 key 进行hash。 Kafka 的默认分区策略:如果指定了 key,key 相同的消息会发送到同一个分区(分区有序);如果没有…...
Powershell 获取电脑保存的所有wifi密码
一. 知识点 netsh wlan show profiles 用于显示计算机上已保存的无线网络配置文件 Measure-Object 用于统计数量 [PSCustomObject]{ } 用于创建Powershell对象 [math]::Round 四舍五入 Write-Progress 显示进度条 二. 代码 只能获取中文Windows操作系统的wifi密码如果想获取…...
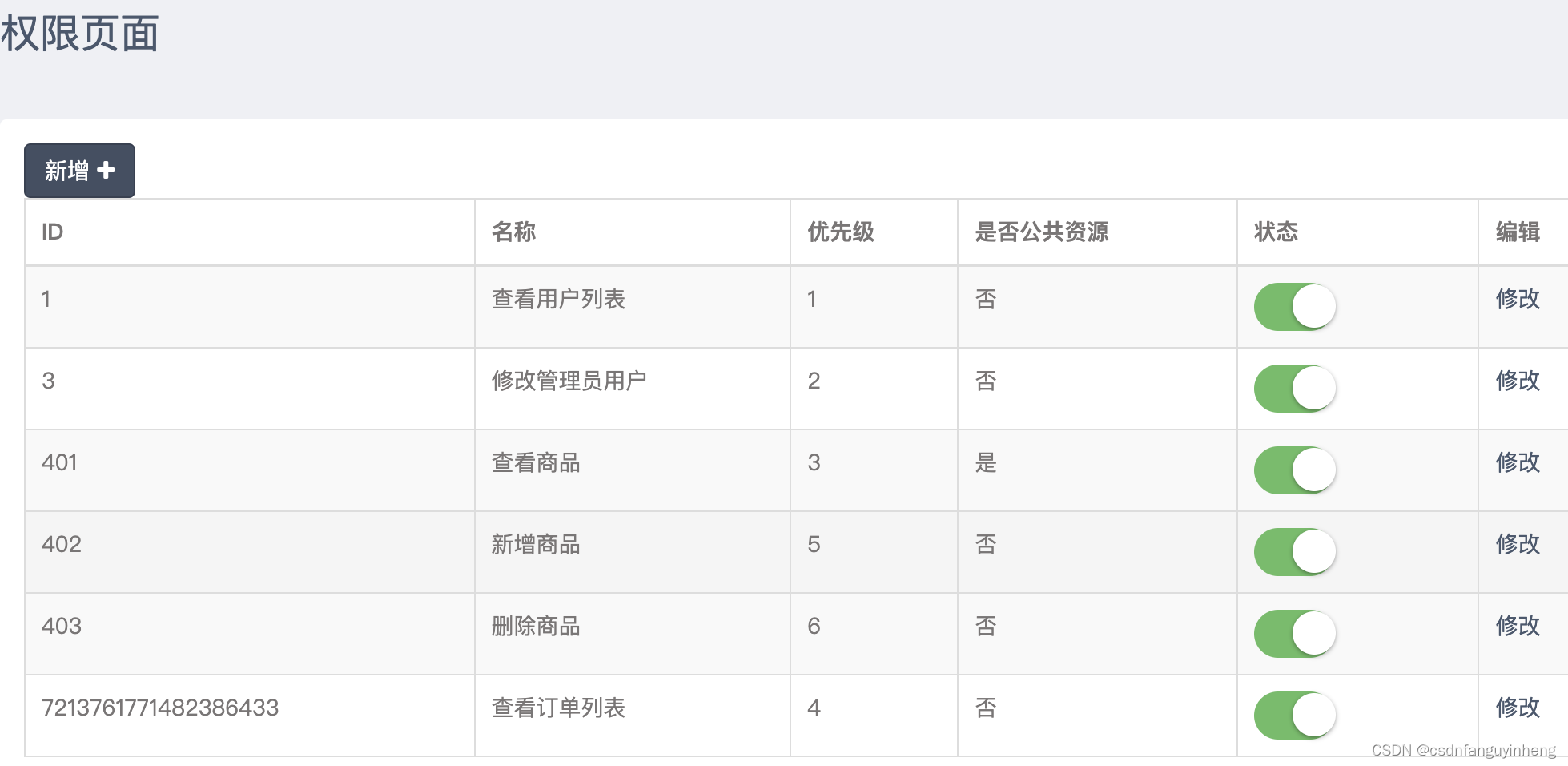
golang结合neo4j实现权限功能设计
neo4j 是非关系型数据库之图形数据库,这里不再赘述。 传统关系数据库基于rbac实现权限, user ---- role ------permission,加上中间表共5张表。 如果再添上部门的概念:用户属于部门,部门拥有 角色,则又多了一层: user-…...

java 参数传递(尤其注意参数是对象的情况)
8大基本数据类型为 值传递 类和数组为 引用传递,传递的是地址 但是要注意虽然类是引用传递,但是要注意,调用方法是新开一个栈 因此如果进行p null或者 Person p new Person()等语句,要格外注意: 如果主函数再次输出…...

拼音字符串相似度
拼音字符串相似度 拼音字符串相似度介绍参考代码**编辑距离****余弦相似度****Jaccard相似度**参考文档拼音字符串相似度 介绍 拼音相似度是指在拼音转换后,两个拼音字符串之间的相似程度。常用的拼音相似度度量方法包括编辑距离、余弦相似度和 Jaccard 相似度等。 编辑距离…...

如何创建一个基本的Mojolicious Web应用:探索Perl的现代Web框架
如何创建一个基本的Mojolicious Web应用:探索Perl的现代Web框架 Mojolicious是一个用Perl编写的简单、优雅的Web开发框架,它提供了一套丰富的工具和方法,让开发者能够快速构建高性能的Web应用。本文将详细介绍如何创建一个基本的Mojolicious…...

FPGA/数字IC复习八股
一、FPGA概念,与数字IC的区别 二、FPGA底层逻辑 三、同步电路、异步电路以及优缺点 四、同步复位、异步复位、异步复位同步释放 深入理解复位---同步复位,异步复位,异步复位同步释放(含多时钟域)_画出支持异步复位dff的电路图…...

Android 简单快速实现 下弧形刻度尺(滑动事件)
效果图: 直接上代码: package com.my.view;import android.content.Context; import android.graphics.Bitmap; import android.graphics.BitmapFactory; import android.graphics.Canvas; import android.graphics.Color; import android.graphics.Pai…...

【Go】常见的变量与常量
变量 常见的变量声明方式 一、声明单个变量的多种方式 1.声明一个变量初始化一个值 //声明变量 默认值是0,var a int//初始化一个值a 1fmt.Println(a) 2. 在初始化的时候省去数据类型,通过值自动匹配当前的变量的数据类型 var b 2fmt.Println(&quo…...

Qt使用sqlite数据库及项目实战
一.sqlite使用介绍 在Qt中使用SQLite数据库非常简单,SQLite是一个轻量级的嵌入式数据库,不需要单独的数据库服务器,完全使用本地文件来存储数据。 当在Qt中使用SQLite数据库时,需要涉及到一些SQL语句以及Qt中的相关函数…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

基于Java+MySQL实现(GUI)客户管理系统
客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息,对客户进行统一管理,可以把所有客户信息录入系统,进行维护和统计功能。可通过文件的方式保存相关录入数据,对…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...

实战三:开发网页端界面完成黑白视频转为彩色视频
一、需求描述 设计一个简单的视频上色应用,用户可以通过网页界面上传黑白视频,系统会自动将其转换为彩色视频。整个过程对用户来说非常简单直观,不需要了解技术细节。 效果图 二、实现思路 总体思路: 用户通过Gradio界面上…...

恶补电源:1.电桥
一、元器件的选择 搜索并选择电桥,再multisim中选择FWB,就有各种型号的电桥: 电桥是用来干嘛的呢? 它是一个由四个二极管搭成的“桥梁”形状的电路,用来把交流电(AC)变成直流电(DC)。…...

论文阅读:Matting by Generation
今天介绍一篇关于 matting 抠图的文章,抠图也算是计算机视觉里面非常经典的一个任务了。从早期的经典算法到如今的深度学习算法,已经有很多的工作和这个任务相关。这两年 diffusion 模型很火,大家又开始用 diffusion 模型做各种 CV 任务了&am…...

Java多线程实现之Runnable接口深度解析
Java多线程实现之Runnable接口深度解析 一、Runnable接口概述1.1 接口定义1.2 与Thread类的关系1.3 使用Runnable接口的优势 二、Runnable接口的基本实现方式2.1 传统方式实现Runnable接口2.2 使用匿名内部类实现Runnable接口2.3 使用Lambda表达式实现Runnable接口 三、Runnabl…...

