贝叶斯估计(1):期末大乱炖
写在前面！
1 先验分布和后验分布
三种信息：总体信息、样本信息、先验信息
总体信息：“总体是正态分布”；样本信息：总体抽取的样本提供的信息，是最新鲜的信息；先验信息：在抽样之前就知道的关于统计问题的一些信息【来源于历史资料等】
贝叶斯公式
离散形式：
几个公式：
先验分布：
样本信息的综合：
三个信息的综合：
对进行估计：
求后验分布！！！
【1】连续时（先验分布）
（1）写出先验分布，如果不知道按照均匀分布处理
（2）计算样本X 和参数的联合分布
样本似然函数 乘以 先验信息密度函数
（3）计算X的边际密度【m(x)】
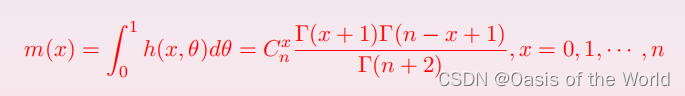
（4）利用贝叶斯公式得到的后验分布
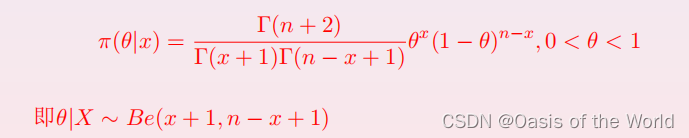
所以的范围在这里就是 大于样本数的的最大值-0.5 小于最小值+0.5
这样就定下了的取值范围咯！！！！
具体视频启发见：已知观测值求后验分布-哔哩哔哩_bilibili
【2】离散
共轭先验分布
【1】正态分布[指的是样本]的共轭先验分布[先验和后验都是]是正态分布(之间的关系)
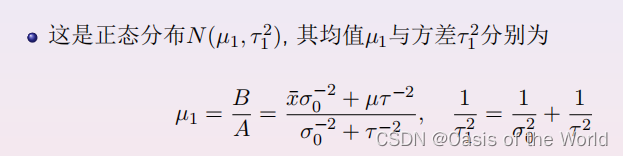
【2】二项分布中的成功概率
的共轭先验分布式贝塔分布
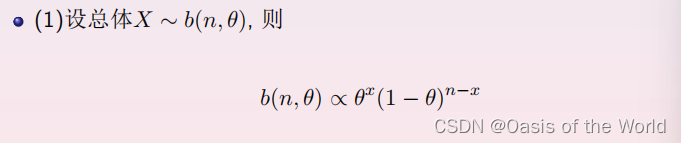
【3】泊松分布的均值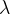
的共轭先验分布是伽马分布
是二项分布的进化，X是发生的次数，那么当抽取样本时，就是总次数！！！！【可见例题5.3.1】
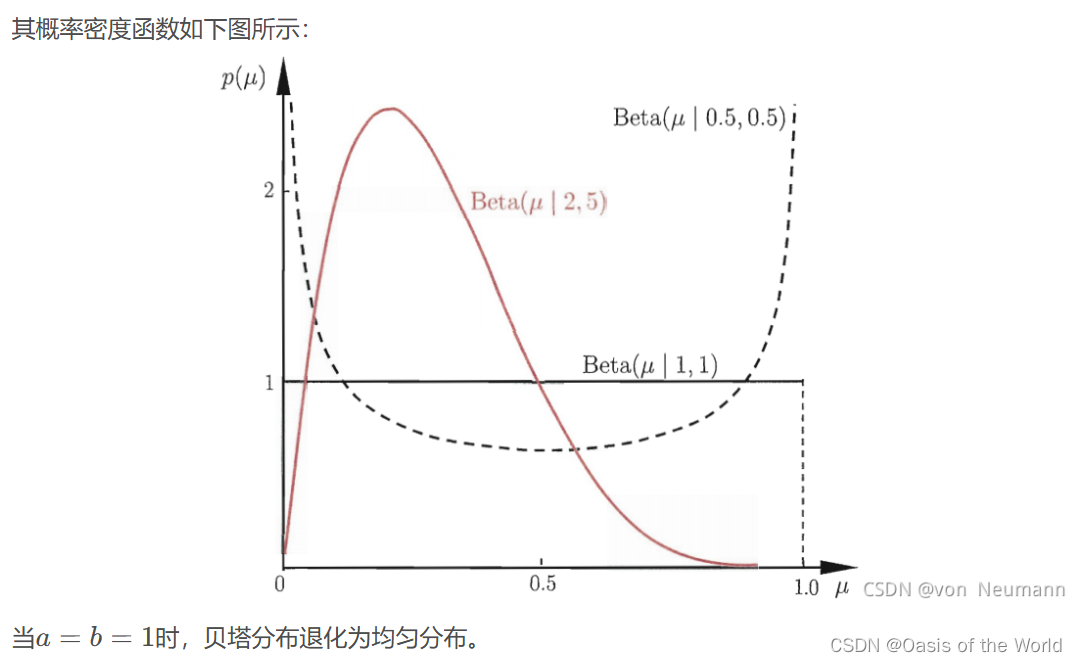
贝塔分布
伽马分布
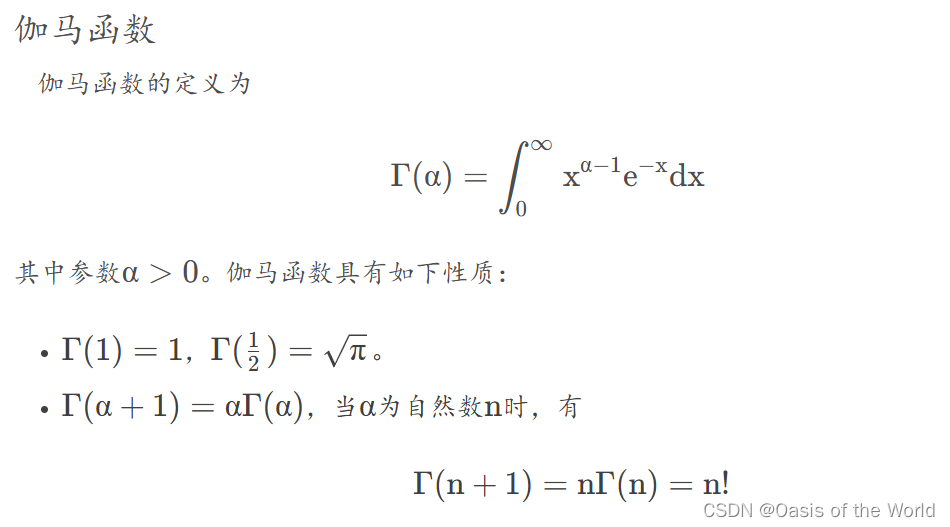
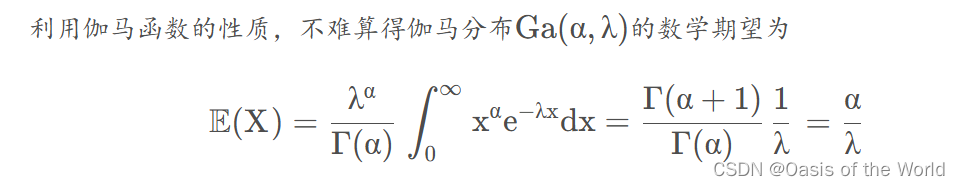
特例：
先验分布超参数的确定
【1】利用先验矩
【2】利用先验分位数
【3】利用先验矩和先验分位数
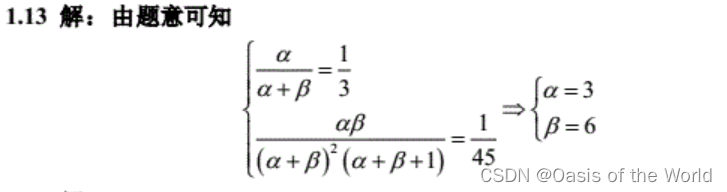
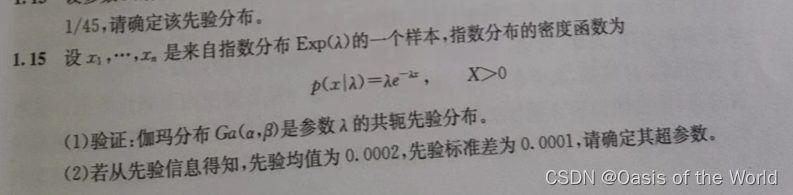
充分统计量【更方便的计算出后验分布！】
作用：
应用：
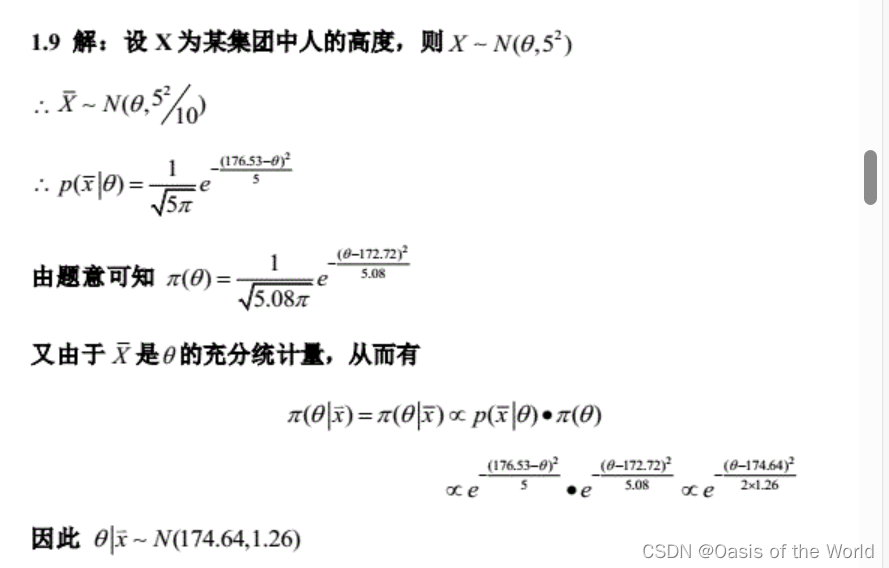
p（x|）是没有办法计算出来的因为，不知道具体取值的情况，但是p（
|
）是知道的
2 贝叶斯推断
存在意义：
2.1 条件方法
2.2 估计
2.2.1 贝叶斯估计
例题1
例题2
例题3
贝叶斯假设 是假设是均匀分布，当都为1 的时候贝塔分布退化成均匀分布
例题4
最大的取值不能超过观察值哦！！！
2.2.2 贝叶斯误差估计
后验均方误差的均值！
例题1 ！！！！（先验分布是离散的）
后验密度达到最大的时候所对应的 是最大后验估计
后验分布期望值是后验分布均值
例题2 （先验分布是连续的贝塔分布）
众数算出来的值其实就是贝塔分布函数达到最大时自变量的取值！！！！
2.3 区间估计
不用寻找枢轴量直接用后验分布就可以！！
例题1
110.38-1.96*8.32 = 94.07
110.38+1.96*8.32 = 126.69
2.4 假设检验
2.4.1 假设检验
接受最大后验概率的假设！！！！
例题1
计算出后验分布！！
均匀
2.4.2 贝叶斯因子
后验概率比较的方法！
后验机会比、前验机会比！可见2.4.4 例题2
贝叶斯因子表示数据X支持原假设的程度！
2.4.3 简单对简单【先计算贝叶斯因子】
例题1
2.4.4 复杂对复杂【计算后验概率比】
例题2
不用计算器的话：就是先标准化然后查表！
贝叶斯因子小这就不可以！
2.4.5 简单对复杂【先计算贝叶斯因子】
例题3
2.4.6 多重假设检验
例题4
谁大接受谁！
2.5 预测
例题5
2.6 似然原理
3 先验分布的确定
3.1 主观概率
3.2 利用先验信息
3.2.1 直方图法（微重要）
例题1
3.2.2 选定先验密度函数形式再估计其超参数
通过矩估计的方法！
例题1延续
例题2
3.2.3 定分位度法和变分位度法【了解即可】
3.3 利用边缘分布确定先验分布
3.3.1 可直接求出边缘分布
例题1
让m(x)达到最大时 ，求出两个超参数的值
3.3.2 混合分布下求出边缘分布类似加权求和
例题2
3.3.3 先验选择的ML-LL方法
例题3 延续3.3.1的例题1
样本是从边缘分布里抽出来的当然可以用于边缘分布超参数的估计！！！！！
3.3.4 先验选择的矩方法
可通过公式进行简化计算！
目标是求出
例题4
到此为止吧，我看不懂.....服了
3.4 无信息先验分布
4 决策中的收益、损失与效用
4.1 决策问题的三要素
4.2 决策准则
4.2.1 行动的容许性
例题1
4.2.2 决策准则【只使用先验信息】
【1】乐观准则（大中选大）
【2】悲观准则（小中选大）
【3】折中准则（加权）
例题
4.3 先验期望准则
例题
例题
这个只计算均值时发现有两个最优行动，因此再计算方差 选择方差小的！！！
P134【课本】
4.3.2 两个性质
都加不变，同一个状态的一行加一样的数不变！
4.4 损失函数
损失函数：“没有转到该赚到的钱！”
4.4.1 从收益到损失
例题【由收益矩阵得到损失矩阵】
损失为，当前位 与赚最多钱时的差距！（状态是一定的！！！）
也是一个状态一算！
例题（已知收益函数的表达式求损失函数！）
对进行积分得到关于a的表达式，然后求出这个表达式的最小值！！！
4.4.2 损失函数下的悲观准则
例题（收益和损失悲观）
注意悲观准则在 收益函数中时（小中选大）；在 损失函数中时（大中选小）
用损失函数进行决策合理一点！
例题
4.4.3 损失函数下的先期望准则
例题
课本【P141】
例题p142
4.5 常用损失函数
4.5.1 常用损失函数
【1】平均损失函数
【2】线性损失函数
【3】0-1损失函数
【4】多元二次损失函数
【5】二行动线性决策问题的损失函数
例题【后序步骤和5.1 中的例题是一样的！】
先求平衡值就是相等的时候的取值！
5 贝叶斯决策
5.1 贝叶斯决策问题定义
先验信息和样本信息 都使用的决策问题！
按照后验平均损失最小 得到贝叶斯决策
优缺点
例题5.1.1P163!!!
让先验期望损失最小是第四章，把弄没，离散的时候是相乘
贝叶斯要在这个机会基础上基础上进行抽样！
5.2 后验风险准则【贝叶斯准则是使用这个的】
5.2.1 后验风险
例题【贝叶斯决策】！！！！！
【1】第四章
【3】贝叶斯
后验分布！：
损失函数的计算后的个数等于：x的取值【抽样后数据的情况】*行动的个数！
损失函数：
行动2：变成只拿出箱子里的两个进行检查 那么需要支付1.6元，然后如果再进行赔偿！
5.2.2 决策函数
5.2.3 后验风险准则
例题5.2.3
例题5.2.4
5.3 常用损失函数下的贝叶斯估计!!!!
5.3.1 平方损失函数下的贝叶斯估计
【1】定理1在平均损失下
【2】定理2在加权平方损失
【3】定理3在多元二次损失函数
例题5.3.1
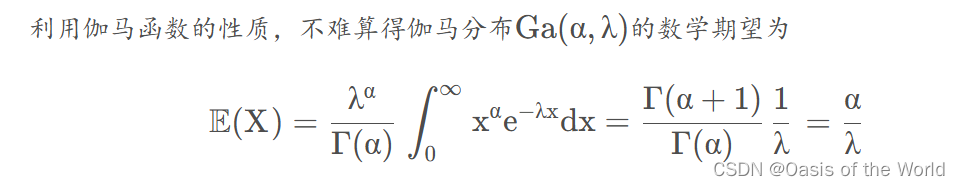
5.3.2 线性损失函数下的贝叶斯估计
【1】定理1
例题5.3.6
后验分布的积分是1
5.3.3 有限个行动问题的假设检验
6 统计决策理论
只使用样本信息！
6.1 风险函数
6.1.1 风险函数
6.1.2 决策函数的最优性
6.1.3 统计决策中的点估计问题
6.1.4 统计决策中的区间估计问题
6.2 容许性
例题
6.3 最小最大准则
例题
例题
相关文章：
贝叶斯估计(1):期末大乱炖
写在前面！ 1 先验分布和后验分布 三种信息：总体信息、样本信息、先验信息 总体信息：“总体是正态分布”；样本信息：总体抽取的样本提供的信息，是最新鲜的信息；先验信息：在抽样之前就…...
电脑找回彻底删除文件？四个实测效果的方法【一键找回】
电脑数据删除了还能恢复吗？可以的，只要我们及时撤销上一步删除操作，还是有几率找回彻底删除文件。 当我们的电脑文件被彻底删除后，尽管恢复的成功率可能受到多种因素的影响，但仍有几种方法可以尝试找回这些文件。本文整…...
java开发报错
查了一下啊。...
基于python 的动态虚拟主机
内容动态，内容通过程序的执行结果返回。 通过编写脚本，完成配置，实现访问页面返回Hello World。 实现步骤： 1、安装python模块 dnf install python3-mod_wsgi 2、编写脚本 在/var/www/cgi-bin/目录下编写脚本： vim…...
绝地求生PUBG没有开始游戏按钮的解决办法
绝地求生是一款特别热门的战术竞技型射击类游戏，游戏中玩家需要在游戏地图上收集各种资源，并在不断缩小的安全区域内持武器对抗其他玩家，让自己生存到最后。当游戏最后场上只剩下一支队伍的时候即可获得游戏胜利。然而一些玩家在游玩绝地求生…...
开始尝试从0写一个项目--前端（一）
基础项目构建 创建VUE初始工程 确保自己下载了node.js和npm node -v //查看node.js的版本 npm -v //查看npm的版本 npm i vue/cli -g //安装VUE CLI 创建 以管理员身份运行 输入：vue ui 就会进入 点击创建 自定义项目名字，选择npm管理 结…...
【Java探索之旅】多态：向上下转型、多态优缺点、构造函数陷阱
文章目录 📑前言一、向上转型和向下转型1.1 向上转型1.2 向下转型 二、多态的优缺点2.1 多态优点2.2 多态缺陷 三、避免避免构造方法中调用重写的方法四、好的习惯🌤️全篇总结 📑前言 在面向对象编程中，向上转型和向下转型是常用…...
Linux上web服务器搭建（Apache、Nginx）
第五章 web服务器 第一节 DNS：对域名进行解析，查询对应的地址 1.1 web服务器简介 www是world wide web的缩写，也就是全球信息广播的意思 1.2.网址及HTTP简介 web服务器提供的这些数据大部分都是文件，那么我们需要在服务器端…...
Django QuerySet对象，exclude()方法
模型参考上一章内容： Django QuerySet对象，filter()方法-CSDN博客 exclude()方法，用于排除符合条件的数据。 1，添加视图函数 Test/app11/views.py from django.shortcuts import render from .models import Postdef index(re…...
Qt/C++音视频开发78-获取本地摄像头支持的分辨率/帧率/格式等信息/mjpeg/yuyv/h264
一、前言 上一篇文章讲到用ffmpeg命令方式执行打印到日志输出，可以拿到本地摄像头设备信息，顺藤摸瓜，发现可以通过执行 ffmpeg -f dshow -list_options true -i video“Webcam” 命令获取指定摄像头设备的分辨率帧率格式等信息，会…...
Go bufio包
bufio包： 带缓冲的I/O操作， 减少系统调用次数， 读取文件、网络数据。 bufio包 是什么 bufio 包是 Go 标准库中的一个非常有用的包，用于提供带缓冲的 I/O 操作。它通过缓冲来提高读取和写入的效率，可以有效减少系统调用…...
C++ 类和对象 拷贝构造函数
一 拷贝构造函数的概念： 拷贝构造函数是一种特殊的构造函数，用于创建一个对象是另一个对象的副本。当需要用一个已存在的对象来初始化一个新对象时，或者将对象传递给函数或从函数返回对象时，会调用拷贝构造函数。 二 拷贝构造函…...
C# —— Math对象
Math 数学类 提供了一些相关数学计算的属性和方法、四舍五入、向上求整、向下求整、开平方，几次方 最大值和最小值 sin cos 绝对值 方法 1.Math 常用的字段 Math.PI double x 2 * 180 / Math.PI; Console.WriteLine(x); 2 Math.Abs() 求绝对值 int a -3; Con…...
Face_recognition实现人脸识别
这里写自定义目录标题 欢迎使用Markdown编辑器一、安装人脸识别库face_recognition1.1 安装cmake1.2 安装dlib库1.3 安装face_recognition 二、3个常用的人脸识别案例2.1 识别并绘制人脸框2.2 提取并绘制人脸关键点2.3 人脸匹配及标注 欢迎使用Markdown编辑器 本文基于face_re…...
1-3分钟爆款视频素材在哪找啊？这9个热门爆款素材网站分享给你
在如今快节奏的时代，短视频已成为吸引观众注意力的黄金手段。然而，要制作出1-3分钟的爆款视频，除了创意和剪辑技巧外，选择合适的素材至关重要。那么，哪里可以找到那些能让你的视频脱颖而出的爆款素材呢？不用…...
武汉免费 【FPGA实战训练】 Vivado入门与设计师资课程
一．背景介绍 当今高度数字化和智能化的工业领域，对高效、灵活且可靠的技术解决方案的需求日益迫切。随着工业 4.0 时代的到来，工业生产过程正经历着前所未有的变革，从传统的机械化、自动化逐步迈向智能化和信息化。在这一背景下&…...
【vite创建项目】
搭建vue3tsvitepinia框架 一、安装vite并创建项目1、用vite构建项目2、配置vite3、找不到模块 “path“ 或其相对应的类型声明。 二、安装element-plus1、安装element-plus2、引入框架 三、安装sass sass-loader1、安装sass 四、安装vue-router-next 路由1、安装vue-router42搭…...
最优化方法 运筹学【】
1.无约束 常用公式 线搜索准则：求步长 精确线搜索（argmin） 最速下降：sd：线性收敛 2.算法 SD dk：付梯度-g newton dk：Gkd-g 二阶收敛，步长为1 阻尼牛顿：步长用先搜…...
探索 WebKit 的动感世界：设备方向和运动支持全解析
探索 WebKit 的动感世界：设备方向和运动支持全解析 随着移动设备的普及，网页应用对设备方向和运动的感知需求日益增长。WebKit 作为众多流行移动浏览器的渲染引擎，提供了对设备方向和运动的全面支持，使得 Web 应用能够根据设备的…...
高考假期预习指南
IT专业入门，高考假期预习指南 对于希望进入IT行业的学生来说，假期是学习信息技术的最佳时机。 在信息化快速发展的时代，IT行业的发展前景广阔，但高技能要求使新生可能感到迷茫。 建议新生制定详细的学习计划，包括了解…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学（Elliptic Curve Cryptography）是基于椭圆曲线数学理论的公钥密码系统，由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA，ECC在相同安全强度下密钥更短（256位ECC ≈ 3072位RSA…...
突破不可导策略的训练难题：零阶优化与强化学习的深度嵌合
强化学习（Reinforcement Learning, RL）是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程，然后使用强化学习的Actor-Critic机制（中文译作“知行互动”机制），逐步迭代求解…...
日语学习-日语知识点小记-构建基础-JLPT-N4阶段（33）：にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段（33）：にする 1、前言（1）情况说明（2）工程师的信仰2、知识点（1） にする1，接续：名词＋にする2，接续：疑问词＋にする3，（A）は（B）にする。（2）復習：（1）复习句子（2）ために ＆ ように（３）そう（４）にする3、…...
解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet，点击确认后如下提示 最终上报fail 解决方法 内核升级导致，需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...
oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异，它们的数据同步要求既要保持数据的准确性和一致性，又要处理好性能问题。以下是一些主要的技术要点： 数据结构差异 数据类型差异ÿ…...
DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API，查询的是单条数据，比如根据主键ID查询用户信息，sql如下： select id, name, age from user where id #{id}API默认返回的数据格式是多条的，如下： {&qu…...
代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币，另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额，返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...
【C++进阶篇】智能指针
C内存管理终极指南：智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...
全面解析数据库：从基础概念到前沿应用
在数字化时代，数据已成为企业和社会发展的核心资产，而数据库作为存储、管理和处理数据的关键工具，在各个领域发挥着举足轻重的作用。从电商平台的商品信息管理，到社交网络的用户数据存储，再到金融行业的交易记录处理&a…...
前端调试HTTP状态码
1xx（信息类状态码） 这类状态码表示临时响应，需要客户端继续处理请求。 100 Continue 服务器已收到请求的初始部分，客户端应继续发送剩余部分。 2xx（成功类状态码） 表示请求已成功被服务器接收、理解并处…...