TPM管理咨询公司甄选指南
在竞争激烈的市场环境中,TPM(全面生产维护)管理咨询公司的重要性日益凸显。然而,如何在众多咨询公司中筛选出最适合自己企业的合作伙伴,成为了许多企业决策者面临的难题。本文将从专业度、行业经验、服务质量和性价比等方面,为您提供一份TPM管理咨询公司甄选指南,助您找到行业内的最佳拍档。

1、明确需求,确定咨询目标
在选择TPM管理咨询公司之前,企业首先需要明确自身的需求和咨询目标。这包括企业当前的生产管理现状、存在的问题、希望达到的效果等。只有明确了需求,才能更有针对性地选择适合的咨询公司。
2、考察专业度与行业经验
在选择TPM管理咨询公司时,企业应当关注其专业度和行业经验。一个优秀的咨询公司应当具备丰富的TPM理论知识和实践经验,能够针对企业的具体情况提供切实可行的解决方案。此外,咨询公司的行业经验也非常重要,它能够帮助企业更好地了解行业的发展趋势和竞争态势。
深圳天行健TPM管理咨询公司拥有一支高素质、专业化的团队。他们具备全面的专业知识和技能,能够在复杂的商业环境中提供准确、可行的建议。团队成员之间的密切合作和良好的沟通也将确保项目的顺利进行。

3、评估服务质量与口碑
服务质量和口碑是选择TPM管理咨询公司时需要重点考虑的因素。企业可以通过查阅咨询公司的案例、客户评价等方式,了解其服务质量和口碑。一个优秀的咨询公司应当能够提供高效、专业的服务,并赢得了客户的广泛好评。
4、关注性价比与长期合作
在选择TPM管理咨询公司时,企业还需要关注性价比和长期合作的可能性。性价比高的咨询公司不仅能够帮助企业节省成本,还能够提供更高质量的服务。同时,长期合作能够帮助企业建立稳定的战略伙伴关系,共同应对市场挑战。
选择一家合适的TPM管理咨询公司对于企业的发展至关重要。通过明确需求、考察专业度与行业经验、评估服务质量与口碑、关注性价比与长期合作等方面,企业可以更有针对性地选择适合自己的咨询公司。同时,成功案例的分享也为企业提供了宝贵的参考经验。希望本文能够为您在选择TPM管理咨询公司时提供有益的启示。
相关文章:

TPM管理咨询公司甄选指南
在竞争激烈的市场环境中,TPM(全面生产维护)管理咨询公司的重要性日益凸显。然而,如何在众多咨询公司中筛选出最适合自己企业的合作伙伴,成为了许多企业决策者面临的难题。本文将从专业度、行业经验、服务质量和性价比等…...

探索 Scikit-Learn:机器学习的强大工具库
Scikit-Learn 探索 Scikit-Learn:机器学习的强大工具库主要功能模块分类(Classification)回归(Regression)聚类(Clustering)降维(Dimensionality Reduction)模型选择&…...

音视频质量评判标准
一、实时通信延时指标 通过图中表格可以看到,如果端到端延迟在200ms以内,说明整个通话是优质的,通话效果就像大家在同一个房间里聊天一样;300ms以内,大多数人很满意,400ms以内,有小部分人可以感…...

如何在vue3中使用scss
一 要使用scss首先需要下载相关的包 可以在终端使用下面的命令下载相关包 npm install -D sass 二 在src文件下新建一个文件夹叫做styles 在文件夹下创建三个文件 index.scss主要用来引用其他文件 reset.scss用来清除默认的样式 variable.scss用来配置全局属性 三 需要在v…...

Gartner发布采用美国防部模型实施零信任的方法指南:七大支柱落地方法
零信任是网络安全计划的关键要素,但制定策略可能会很困难。安全和风险管理领导者应使用美国国防部模型的七大支柱以及 Gartner 研究来设计零信任策略。 战略规划假设 到 2026 年,10% 的大型企业将拥有全面、成熟且可衡量的零信任计划,而 202…...
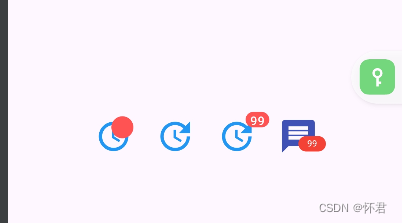
Flutter——最详细(Badge)使用教程
背景 主要常用于组件叠加上圆点提示; 使用场景,消息数量提示,消息红点提示 属性作用backgroundColor红点背景色smallSize设置红点大小isLabelVisible是否显示offset设置红点位置alignment设置红点位置child设置底部组件 代码块 class Badge…...

SQLServer的系统数据库用别的服务器上的系统数据库替换后做跨服务器连接时出现凭证、非对称金钥或私密金钥的资料无效
出错作业背景: 公司的某个sqlserver服务器要做迁移,由于该sqlserver服务器上数据库很多,并且做了很多的job和维护计划,重新安装的sqlserver这些都是空的,于是就想到了把系统4个系统数据库进行替换,然后也把…...

vue前端面试
一 .v-if和v-show的区别 v-if 和 v-show 是 Vue.js 中两个常用的条件渲染指令,它们都可以根据条件决定是否渲染某个元素。但是它们之间存在一些区别。 语法:v-if 和 v-show 的语法相同,都接收一个布尔值作为参数。 <div v-if"show…...

【网络安全】Host碰撞漏洞原理+工具+脚本
文章目录 漏洞原理虚拟主机配置Host头部字段Host碰撞漏洞漏洞场景工具漏洞原理 Host 碰撞漏洞,也称为主机名冲突漏洞,是一种网络攻击手段。常见危害有:绕过访问控制,通过公网访问一些未经授权的资源等。 虚拟主机配置 在Web服务器(如Nginx或Apache)上,多个网站可以共…...

unattended-upgrade进程介绍
unattended-upgrade 是一个用于自动更新 Debian 和 Ubuntu 系统的软件包。这个进程通常用于定期下载并安装安全更新,以保持系统的安全性和稳定性。 具体来说,这个命令 /usr/bin/python3 /usr/bin/unattended-upgrade --download-only 表示运行 unattend…...

SpringBoot 中多例模式的神秘世界:用法区别以及应用场景,最后的灵魂拷问会吗?- 第519篇
历史文章(文章累计500) 《国内最全的Spring Boot系列之一》 《国内最全的Spring Boot系列之二》 《国内最全的Spring Boot系列之三》 《国内最全的Spring Boot系列之四》 《国内最全的Spring Boot系列之五》 《国内最全的Spring Boot系列之六》 《…...
_2024升级版_180)
基于STM32设计的智能婴儿床(ESP8266局域网)_2024升级版_180
基于STM32设计的智能婴儿床(采用STM32F103C8T6)(180) 文章目录 一、设计需求【1】项目功能介绍【2】程序最终的运行逻辑【3】硬件模块组成【4】ESP8266模块配置【5】上位机开发思路【6】系统功能模块划分1.2 项目开发背景1.3 开发工具的选择1.4 系统框架图1.5 系统原理图1.6 硬…...
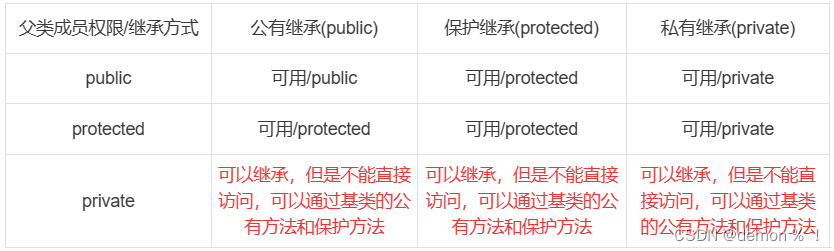
C++(第四天----拷贝函数、类的组合、类的继承)
一、拷贝构造函数(复制构造函数) 1、概念 拷贝构造函数,它只有一个参数,参数类型是本类的引用。如果类的设计者不写拷贝构造函数,编译器就会自动生成拷贝构造函数。大多数情况下,其作用是实现从源对象到目…...

第一课:接口配置IP地址:DHCP模式
希望pc1,pc2,pc3自动分配到ip地址。 实验拓扑: 配置:高级一点的路由器还是手动配置: [R1]int g0/0/0 [R1-g0/0/0]ip address 192.168.1.1 255.255.255.0 打开PC1,切换到DHCP模式,点击应用,再到命令行输入ipconfig&…...

esp32_spfiffs
生成 spiffs image python spiffsgen.py <image_size> <base_dir> <output_file> eg, python spiffsgen.py 0x2000 ./folder hello.bin Arduino 的库有例子可以直接用于 OTA 升级 spiffs 分区 HTTPUpdateResult HTTPUpdate::updateSpiffs(HTTPClient &h…...
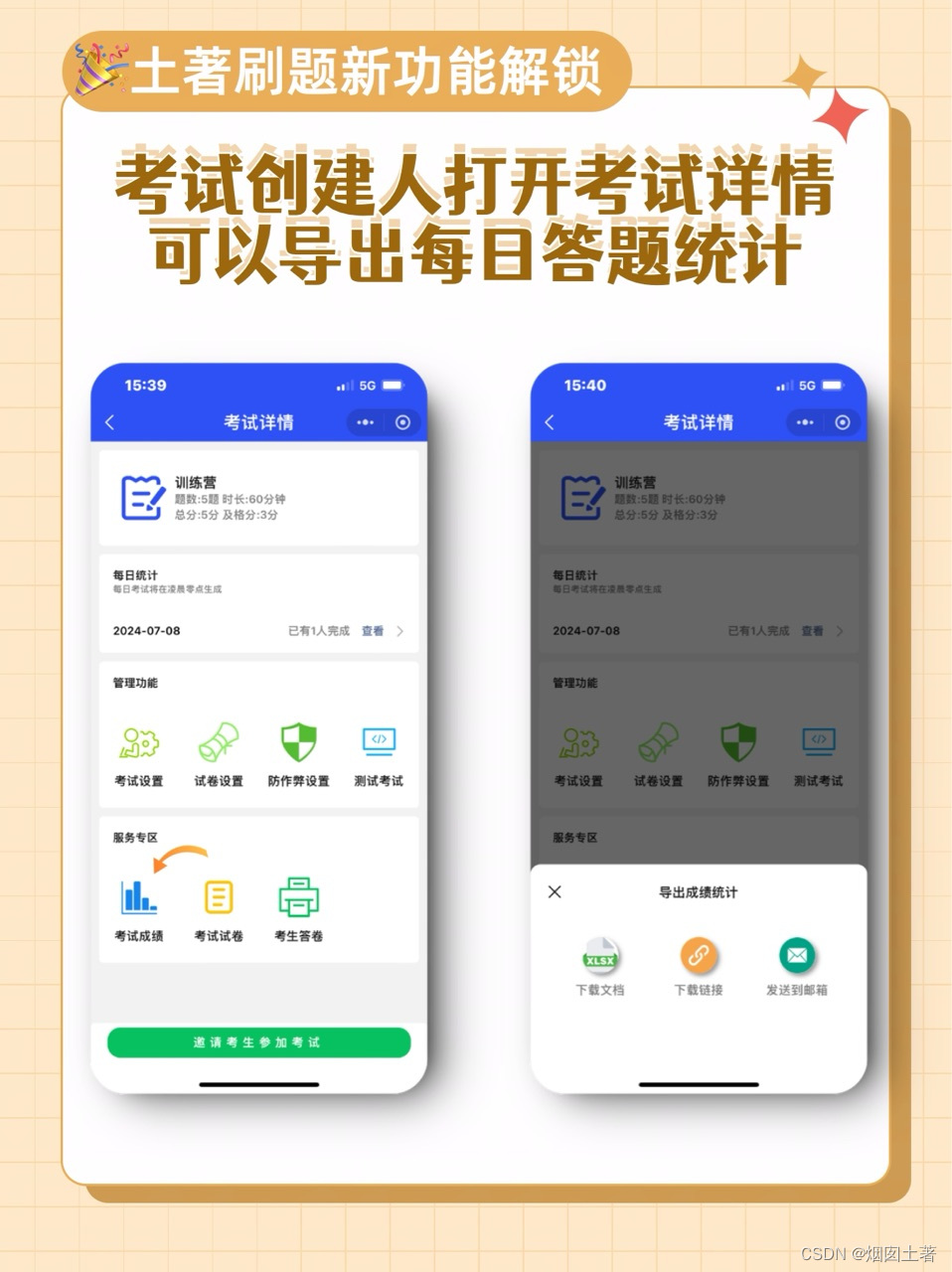
每日一练全新考试模式解锁|考试升级
🙋频繁有小伙伴咨询:我想举办一场历时一个月的答题活动,学生可以每天打开答题,活动完结后可以导出每天的答题成绩 此前我们都会让小伙伴创建30场考试,然后使用批量分享功能组合起来,对外分享一个链接就可以…...

pyqt5图片分辨率导致的界面过大的问题
项目场景:pyqt5的图片分辨率和屏幕分辨率问题 提示:这里简述项目相关背景:图片分辨率:500*500;显示屏分辨率:600;导致界面显示不全; 在其他高分辨率显示屏中没有这个问题。 问题描述…...

(三)前端javascript中的数据结构之集合
集合的特点 1.无序 2.唯一性 3.不可重复 集合相对于前面几种数据结构,比较简单好理解,看看代码实现就能知道他的用法了 集合的创建 function MySet() {this.item {}; } MySet.prototype.has function (value) {return value in this.item; };//增 M…...
VuePress 的更多配置
现在,读者应该对 VuePress、主题和插件等有了基本的认识,除了插件,VuePress 自身也有很多有用的配置,这里简单说明下。 VuePress 的介绍 在介绍了 VuePress 的基本使用、主题和插件的概念之后,我们再来看看官…...

问题解决|Python 代码的组织形式与编码规范
一、Python中组织形式 (一)组织形式(函数,类,模块,包,库)概览 (1)概览 组织形式描述特点或用途例子函数一段具有特定功能的代码块,可以接受参数…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...

JavaScript 数据类型详解
JavaScript 数据类型详解 JavaScript 数据类型分为 原始类型(Primitive) 和 对象类型(Object) 两大类,共 8 种(ES11): 一、原始类型(7种) 1. undefined 定…...

区块链技术概述
区块链技术是一种去中心化、分布式账本技术,通过密码学、共识机制和智能合约等核心组件,实现数据不可篡改、透明可追溯的系统。 一、核心技术 1. 去中心化 特点:数据存储在网络中的多个节点(计算机),而非…...

xmind转换为markdown
文章目录 解锁思维导图新姿势:将XMind转为结构化Markdown 一、认识Xmind结构二、核心转换流程详解1.解压XMind文件(ZIP处理)2.解析JSON数据结构3:递归转换树形结构4:Markdown层级生成逻辑 三、完整代码 解锁思维导图新…...

ui框架-文件列表展示
ui框架-文件列表展示 介绍 UI框架的文件列表展示组件,可以展示文件夹,支持列表展示和图标展示模式。组件提供了丰富的功能和可配置选项,适用于文件管理、文件上传等场景。 功能特性 支持列表模式和网格模式的切换展示支持文件和文件夹的层…...
