数据结构与算法基础-学习-15-二叉树
一、二叉树定义
二叉树是N(N>=0)个节点的有限集,它可能是空集或者由一个根节点及两棵互不相交的分别称作这个根的左子树和右子树的二叉树组成。
二、二叉树特点
1、每个节点最多两个孩子。(也就是二叉树的度小于等于2)
2、根有左右之分,不可颠倒。
3、二叉树可以是空集,根的左子树或右子树可以为空。
三、图示
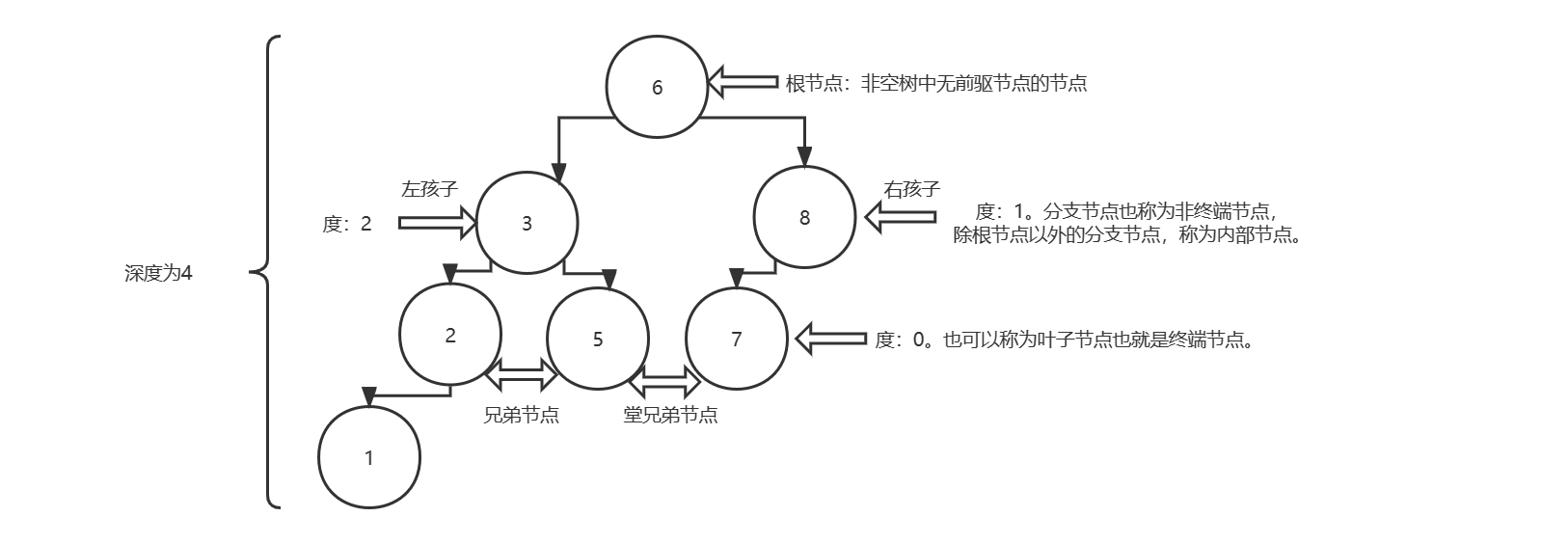
四、二叉树性质
1、性质一
深度为k的二叉树至多有2的k次方再减一。
推导第一层有一个(2的0次方),第二层最多有两个(2的1次方),第三层最多有四个(2的2次方)。我们可以用等比求和公式:Sn=(a1-an*q)/(1-q)=(1-4*2)/(-1)=7。
2、性质二
在二叉树的第i层上至多有2的(i-1)次方个节点。
3、性质三
对任何一棵二叉树T,如果其叶子数为n0,度为2的节点数为n2,n0=n2+1。
五、特殊形式的二叉树
1、满二叉树
(1)定义和图示
满二叉树在相同深度的二叉树中结点数和叶子结点数是最多的。
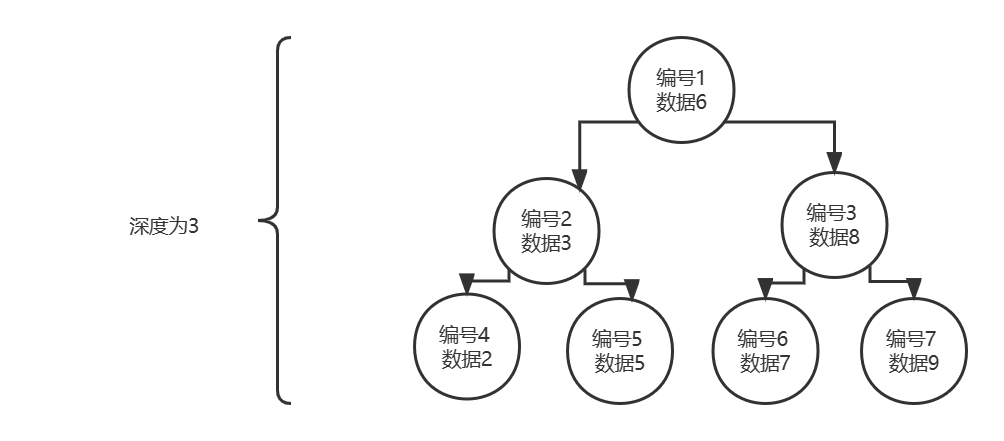
2、完全二叉树
(1)定义和图示
深度为k的具有n个结点的二叉树,当且仅当其每一个结点都与深度为k的满二叉树中编号为1~n的结点一一对应时,称之为完全二叉树。
满二叉树是完全二叉树,完全二叉树不一定是满二叉树。
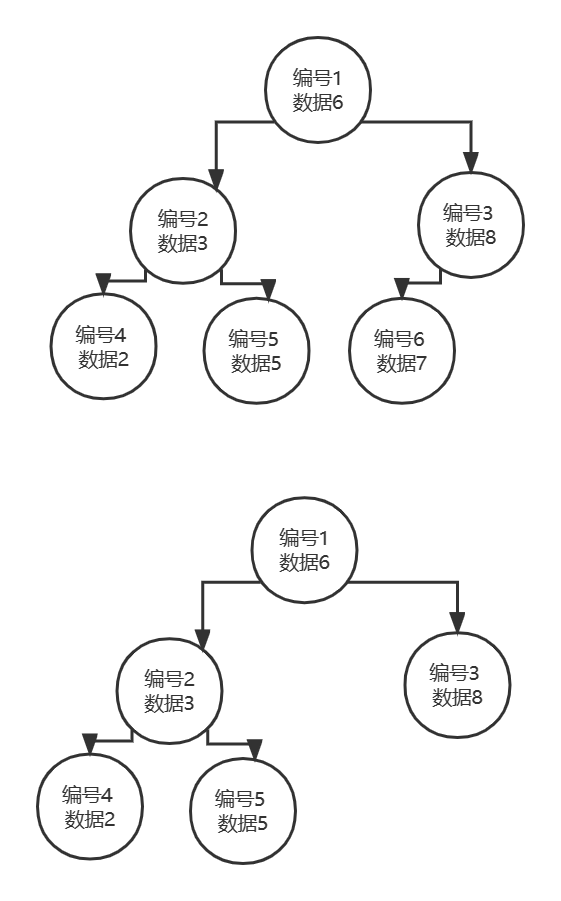
(2)特性一
具有n个结点的完全二叉树深度为log(2)(n)(向下取整)+1。
(3)特性二
如果对一棵有n个结点的完全二叉树(深度为log(2)(n)(向下取整)+1)的结点按照层序编号(从上到下,从左到右),则对于任一结点i(1<=i<=n),有:
(1)如果i=1,则结点i是二叉树的根,无双亲。如果是i>1,则双亲是结点i/2再向下取整。
(2)如果2i>n,则结点i为叶子节点,无左孩子;否则,其左孩子是结点2i。
(3)如果2i+1>n,则结点i无右孩子。否则,其右孩子是结点2i+1。
六、二叉搜索树
二叉搜索树(Binary Search Tree)简称BST,如果结点的左子树不为空,则左子树存储的数据需要小于结点存储的数据。如果结点的右子树不为空,则右子树存储的数据需要大于结点存储的数据。
二叉搜索树的中序遍历,最终会形成一个从小到大排列的数组。
将数组{6,3,8,2,5,1,7}变为一棵BST,BST如下图:
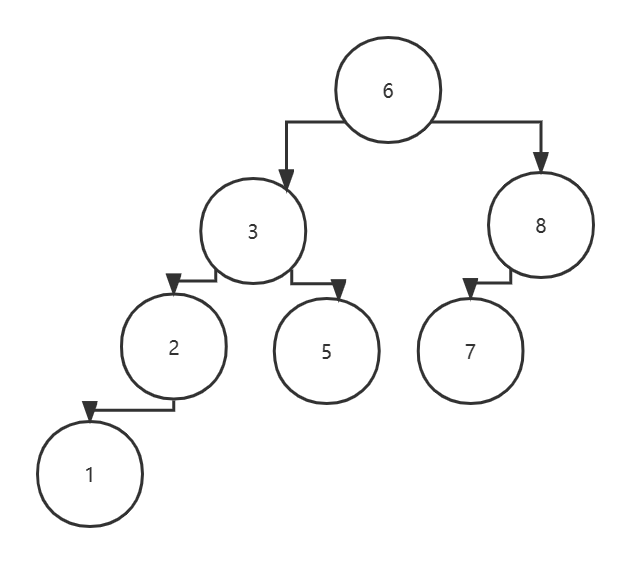
七、BST结构体
1、BinaryTreeNode
(1)描述
二叉树结点定义,Data数据域,LeftNodePtr左子树指针,RightNodePtr右子树指针,JudegeTreeUsedArray在非递归后续遍历时用到,其他并未用到,数组长度2,分别表示左右子树状态
,JUDGE_TREE_UNUSED为此树没遍历,JUDGE_TREE_USED为此树遍历。
(2)定义
#define JUDGE_TREE_UNUSED 0
#define JUDGE_TREE_USED 1
#define JUDGE_TREE_ARRAY_LEN 2typedef int ElemType;typedef struct BinaryTreeNode
{ElemType Data;struct BinaryTreeNode* LeftNodePtr;struct BinaryTreeNode* RightNodePtr;int JudegeTreeUsedArray[JUDGE_TREE_ARRAY_LEN];//为了实现非递归后序遍历使用的数据,其他遍历方法未使用。
}BinaryTreeNode, *BinaryTreeNodePtr;2、BinaryTree
(1)描述
二叉树结点定义,NodePtr树的根节点,TreeNodeNum树的总结点数。
(2)定义
typedef struct BinaryTree
{BinaryTreeNodePtr NodePtr;BinaryTreeSizeType TreeNodeNum;
}BinaryTree;八、BST函数
其中前中后序遍历非递归方法实现需要用到顺序栈,可以参考之前写的博客《数据结构与算法基础-学习-09-线性表之栈的理解、初始化顺序栈、判断顺序栈空、获取顺序栈长度的实现》和《数据结构与算法基础-学习-10-线性表之顺序栈的清理、销毁、压栈、弹栈》
1、NewBinaryTreeNode
(1)描述
生成一个新节点,把数据放入结点中。
(2)定义
BinaryTreeNodePtr NewBinaryTreeNode(ElemType InputData)
{BinaryTreeNodePtr NewNodePtr = (BinaryTreeNodePtr)MyMalloc(sizeof(BinaryTreeNode));NewNodePtr->Data = InputData;NewNodePtr->LeftNodePtr = NULL;NewNodePtr->RightNodePtr = NULL;memset(NewNodePtr->JudegeTreeUsedArray, JUDGE_TREE_UNUSED, sizeof(int) * JUDGE_TREE_ARRAY_LEN);//非递归前序遍历使用Log("New Binary Tree Node : OK\n",Debug);return NewNodePtr;
}(3)参数介绍
参数名 | 描述 |
InputData | ElemType类型的数据。 |
2、GetBinaryTreeNodeNum
(1)描述
获取BST的总结点数。
(2)定义
BinaryTreeSizeType GetBinaryTreeNodeNum(BinaryTree* BT)
{JudgeAllNullPointer(BT);return BT->TreeNodeNum;
}(3)参数介绍
参数名 | 描述 |
BT | BinaryTree*类型的BST指针。 |
3、CmpElemTypeData
(1)描述
对比ET1和ET2的大小。
(2)定义
#define LARGE_FLAG 0
#define LITTLE_FLAG 1
#define EQUAL_FLAG 2Status CmpElemTypeData(ElemType ET1, ElemType ET2)
{if(ET1 > ET2){return LARGE_FLAG;}else if(ET1 < ET2){return LITTLE_FLAG;}else{return EQUAL_FLAG;}
}(3)参数介绍
参数名 | 描述 |
ET1 | ElemType类型数据。 |
ET2 | ElemType类型数据。 |
4、AddBinarySearchTreeNode
(1)描述
将InputData数据放入BST中。
(2)定义
//假设二叉搜索树中没有相同元素,且数据都是正数,根节点大于左子树,小于右子树。
Status AddBinarySearchTreeNode(BinaryTree* BT, ElemType InputData)
{JudgeAllNullPointer(BT);if(BT->NodePtr == NULL){BT->NodePtr = NewBinaryTreeNode(InputData);BT->TreeNodeNum++;Log("Add BST Node : OK\n",Debug);return SuccessFlag;}BinaryTreeNodePtr TmpPtr = BT->NodePtr;while(TmpPtr){if(CmpElemTypeData(TmpPtr->Data, InputData) == LARGE_FLAG){if(TmpPtr->LeftNodePtr == NULL){TmpPtr->LeftNodePtr = NewBinaryTreeNode(InputData);BT->TreeNodeNum++;Log("Add BST Node : OK\n",Debug);return SuccessFlag;}TmpPtr = TmpPtr->LeftNodePtr;}else if(CmpElemTypeData(TmpPtr->Data, InputData) == LITTLE_FLAG){if(TmpPtr->RightNodePtr == NULL){TmpPtr->RightNodePtr = NewBinaryTreeNode(InputData);BT->TreeNodeNum++;Log("Add BST Node : OK\n",Debug);return SuccessFlag;}TmpPtr = TmpPtr->RightNodePtr;}else{Log("AddBinarySearchTreeNode function not supported : same element.\n",Debug);Log("Add BST Node : Fail\n",Debug);return FailFlag;}}return FailFlag;
}(3)参数介绍
参数名 | 描述 |
BT | BinaryTree*类型的BST。 |
InputData | ElemType类型的输入数据。 |
5、NewBinarySearchTree
(1)描述
给一个数组生成一棵BST。
(2)定义
Status NewBinarySearchTree(BinaryTree* BT, ElemType* Array)
{BinaryTreeSizeType i; for(i = 0; i < InsertDataArrayLen; i++){AddBinarySearchTreeNode(BT, Array[i]);}Log("New Binary Search Tree: OK\n",Info);return SuccessFlag;
}(3)参数介绍
参数名 | 描述 |
BT | BinaryTree*类型的BST。 |
Array | ElemType*类型的输入数据数据。 |
6、InitBinaryTree
(1)描述
初始化二叉树。
(2)定义
Status InitBinaryTree(BinaryTree* BT)
{JudgeAllNullPointer(BT);BT->TreeNodeNum = 0;Log("Init Binary Tree : OK\n",Info);return SuccessFlag;
}(3)参数介绍
参数名 | 描述 |
BT | BinaryTree*类型的BST。 |
7、InOrderTraverseNoRecursion
(1)描述
中序遍历非递归方法实现。
(2)定义
Status InOrderTraverseNoRecursion(BinaryTreeNodePtr RootPTR)
{if(RootPTR == NULL){return SuccessFlag;}SqStack* S = (SqStack*)MyMalloc(sizeof(SqStack));BinaryTreeNodePtr TmpPtr = RootPTR;InitSqStack(S);while(TmpPtr || JudgeSqStackIsEmpty(S) == FailFlag)//如果指针和栈为空退出循环{if(TmpPtr)//如果节点不为空,说明有数据,中序遍历:左根右。将根压入栈,指针指向左子树。{PushSqStack(S, *TmpPtr);TmpPtr = TmpPtr->LeftNodePtr;}else//如果节点为空,说明左子树没有数据,弹栈获取上一层节点指针,获取根节点数据,再将指针指向右子树。{BinaryTreeNodePtr TmpPtr1 = (BinaryTreeNodePtr)MyMalloc(sizeof(BinaryTreeNode));PopSqStack(S, TmpPtr1);Insert2GlobalArray(&GA,TmpPtr1->Data);TmpPtr = TmpPtr1->RightNodePtr;free(TmpPtr1);TmpPtr1 = NULL;}}DestroyStack(S);return SuccessFlag;
}(3)参数介绍
参数名 | 描述 |
RootPTR | BinaryTreeNodePtr类型根节点。 |
8、PreOrderTraverseNoRecursion
(1)描述
前序遍历非递归方法实现。
(2)定义
Status PreOrderTraverseNoRecursion(BinaryTreeNodePtr RootPTR)
{if(RootPTR == NULL){return SuccessFlag;}SqStack* S = (SqStack*)MyMalloc(sizeof(SqStack));BinaryTreeNodePtr TmpPtr = RootPTR;InitSqStack(S);while(TmpPtr || JudgeSqStackIsEmpty(S) == FailFlag)//如果指针和栈为空退出循环{if(TmpPtr){PushSqStack(S, *TmpPtr);Insert2GlobalArray(&GA,TmpPtr->Data);TmpPtr = TmpPtr->LeftNodePtr;}else{BinaryTreeNodePtr TmpPtr1 = (BinaryTreeNodePtr)MyMalloc(sizeof(BinaryTreeNode));PopSqStack(S, TmpPtr1);TmpPtr = TmpPtr1->RightNodePtr;free(TmpPtr1);TmpPtr1 = NULL;}}DestroyStack(S);return SuccessFlag;
}(3)参数介绍
参数名 | 描述 |
RootPTR | BinaryTreeNodePtr类型根节点。 |
9、PostOrderTraverseNoRecursion
(1)描述
后序遍历非递归方法实现。
(2)定义
Status PostOrderTraverseNoRecursion(BinaryTreeNodePtr RootPTR)
{if(RootPTR == NULL){return SuccessFlag;}SqStack* S = (SqStack*)MyMalloc(sizeof(SqStack));BinaryTreeNodePtr TmpPtr = RootPTR;InitSqStack(S);while(TmpPtr || JudgeSqStackIsEmpty(S) == FailFlag)//如果指针和栈为空退出循环{if(TmpPtr && TmpPtr->JudegeTreeUsedArray[0] == JUDGE_TREE_UNUSED){TmpPtr->JudegeTreeUsedArray[0] = JUDGE_TREE_USED;PushSqStack(S, *TmpPtr);TmpPtr = TmpPtr->LeftNodePtr;}else{BinaryTreeNodePtr TmpPtr1 = (BinaryTreeNodePtr)MyMalloc(sizeof(BinaryTreeNode));PopSqStack(S, TmpPtr1);if((TmpPtr1->JudegeTreeUsedArray)[JUDGE_TREE_ARRAY_LEN-1] == JUDGE_TREE_USED){//printf("%d %d\n",TmpPtr1->JudegeTreeUsedArray[0],TmpPtr1->JudegeTreeUsedArray[JUDGE_TREE_ARRAY_LEN-1]);Insert2GlobalArray(&GA,TmpPtr1->Data);//PrintfGlobalArray(&GA,"tmp");if(PopSqStack(S, TmpPtr1) == FailFlag)//如果栈是空的,说明已经完成所有节点的遍历,跳出循环。{free(TmpPtr1); TmpPtr1 = NULL;break;}}TmpPtr = TmpPtr1->RightNodePtr;TmpPtr1->JudegeTreeUsedArray[JUDGE_TREE_ARRAY_LEN-1] = JUDGE_TREE_USED;PushSqStack(S, *TmpPtr1);free(TmpPtr1);TmpPtr1 = NULL;}}DestroyStack(S);return SuccessFlag;
}(3)参数介绍
参数名 | 描述 |
RootPTR | BinaryTreeNodePtr类型根节点。 |
10、InOrderTraverse
(1)描述
中序遍历递归方法实现。
(2)定义
Status InOrderTraverse(BinaryTreeNodePtr RootPTR)
{if(RootPTR == NULL){return SuccessFlag;}else{InOrderTraverse(RootPTR->LeftNodePtr);//printf("%d\n",RootPTR->Data);Insert2GlobalArray(&GA,RootPTR->Data);InOrderTraverse(RootPTR->RightNodePtr);}return SuccessFlag;
}(3)参数介绍
参数名 | 描述 |
RootPTR | BinaryTreeNodePtr类型根节点。 |
11、PreOrderTraverse
(1)描述
前序遍历递归方法实现。
(2)定义
Status PreOrderTraverse(BinaryTreeNodePtr RootPTR)
{if(RootPTR == NULL){return SuccessFlag;}else{Insert2GlobalArray(&GA,RootPTR->Data);PreOrderTraverse(RootPTR->LeftNodePtr);PreOrderTraverse(RootPTR->RightNodePtr);}return SuccessFlag;
}(3)参数介绍
参数名 | 描述 |
RootPTR | BinaryTreeNodePtr类型根节点。 |
12、PostOrderTraverse
(1)描述
后序遍历递归方法实现。
(2)定义
Status PostOrderTraverse(BinaryTreeNodePtr RootPTR)
{if(RootPTR == NULL){return SuccessFlag;}else{PostOrderTraverse(RootPTR->LeftNodePtr);PostOrderTraverse(RootPTR->RightNodePtr);Insert2GlobalArray(&GA,RootPTR->Data);}return SuccessFlag;
}(3)参数介绍
参数名 | 描述 |
RootPTR | BinaryTreeNodePtr类型根节点。 |
九、LINUX环境测试
[gbase@czg2 Tree]$ make
gcc -Wall -g ../Log/Log.c BinaryTree.c main.c -o TestBinaryTree -I ../Log/[gbase@czg2 Tree]$ ./TestBinaryTree
2023-3--[Info]--Init Global Array : OK
2023-3--[Info]--Init Binary Tree : OK
2023-3--[Info]--New Binary Search Tree : OK
2023-3--[Info]--PreOrderTraverse : [6 ,3 ,2 ,1 ,5 ,8 ,7 ], CurSize : 7
2023-3--[Info]--InOrderTraverse : [1 ,2 ,3 ,5 ,6 ,7 ,8 ], CurSize : 7
2023-3--[Info]--PostOrderTraverse : [1 ,2 ,5 ,3 ,7 ,8 ,6 ], CurSize : 7
2023-3--[Info]--PreOrderTraverseNoRcs : [6 ,3 ,2 ,1 ,5 ,8 ,7 ], CurSize : 7
2023-3--[Info]--InOrderTraverseNoRcs : [1 ,2 ,3 ,5 ,6 ,7 ,8 ], CurSize : 7
2023-3--[Info]--PostOrderTraverseNoRcs : [1 ,2 ,5 ,3 ,7 ,8 ,6 ], CurSize : 7相关文章:

数据结构与算法基础-学习-15-二叉树
一、二叉树定义二叉树是N(N>0)个节点的有限集,它可能是空集或者由一个根节点及两棵互不相交的分别称作这个根的左子树和右子树的二叉树组成。二、二叉树特点1、每个节点最多两个孩子。(也就是二叉树的度小于等于2)2…...
接口测试要测试什么?
一. 什么是接口测试?为什么要做接口测试? 接口测试是测试系统组件间接口的一种测试。接口测试主要用于检测外部系统与系统之间以及内部各个子系统之间的交互点。测试的重点是要检查数据的交换,传递和控制管理过程,以及系统间的相互…...

2023.03.12学习总结
项目部分写了内外菜单栏的伸缩,更新了导航栏,新增配置,scss变量 提交记录 学习了scss的使用和配置 ,设置了scss全局变量,组件样式 给element-plus配置了主题颜色,配置到了全局 http://t.csdn.cn/FhZYa …...

数据结构入门6-1(图)
目录 注 图的定义 图的基本术语 图的类型定义 图的存储结构 邻接矩阵 1. 邻接矩阵表示法 2. 使用邻接矩阵表示法创建无向网 3. 邻接矩阵表示法的优缺点 邻接表 1. 邻接表表示法 2. 通过邻接表表示法创建无向图 3. 邻接表表示法的优缺点 十字链表(有向…...
把C#代码上传到NuGet,大佬竟是我自己!!!
背景 刚发表完一篇博客总结自己写标准化C#代码的心历路程,立马就产生一个问题,就是我写好标准化代码后,一直存放磁盘的话,随着年月增加,代码越来越多,项目和版本的管理就会成为一个令我十分头疼的难题&…...

解决前端“\n”不换行问题
在日常开发过程中,换行显示是一种很常见的应用需求,但是偶然发现,有时候使用 "\n"并不会换行显示,只会被识别为空格,如下图。 通过上图可以看出,"\n"它被识别成了一个空格显示&#…...
Python打包成exe,文件太大问题解决办法(比保姆级还保姆级)
首先我要说一下,如果你不在乎大小,此篇直接别看了,因为我写过直接打包的,就多20M而已,这篇就别看了,点击查看不在乎大小直接打包这篇我觉得简单的令人发指 不废话,照葫芦画瓢就好 第1步&#…...

CSS弹性布局flex属性整理
1.align-items align-items属性:指定弹性布局内垂直方向的对齐方向。 常用属性: center 垂直居中展示 flex-start 头部对齐 flex-end 底部对齐 2. justify-content justify-content属性:属性(水平)对齐弹…...

14个你需要知道的实用CSS技巧
让我们学习一些实用的 CSS 技巧,以提升我们的工作效率。这些 CSS 技巧将帮助我们开发人员快速高效地构建项目。 现在,让我们开始吧。 1.CSS :in-range 和 :out-of-range 伪类 这些伪类用于在指定范围限制之内和之外设置输入样式。 (a) : 在范围内 如…...

【Flutter从入门到入坑之四】构建Flutter界面的基石——Widget
【Flutter从入门到入坑】Flutter 知识体系 【Flutter从入门到入坑之一】Flutter 介绍及安装使用 【Flutter从入门到入坑之二】Dart语言基础概述 【Flutter从入门到入坑之三】Flutter 是如何工作的 WidgetWidget 是什么呢?Widget 渲染过程WidgetElementRenderObjectR…...
中职网络空间安全windows渗透
目录 B-1:Windows操作系统渗透测试 1.通过本地PC中渗透测试平台Kali对服务器场景Windows进行系统服务及版本扫描渗透测试,并将该操作显示结果中Telnet服务对应的端口号作为FLAG提交;编辑 2.通过本地PC中渗透测试平台Kali对服务器场景Wind…...
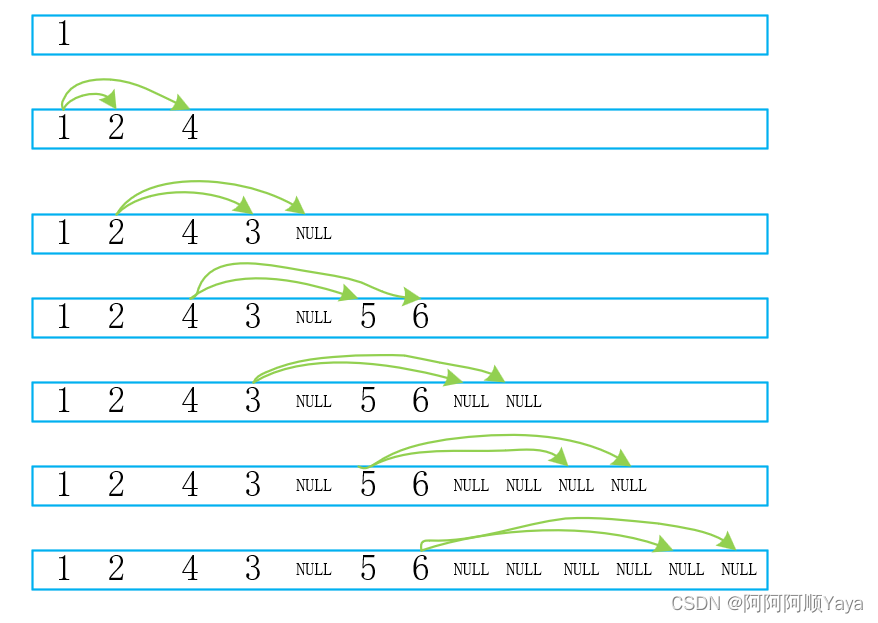
普通二叉树的操作
普通二叉树的操作1. 前情说明2. 二叉树的遍历2.1 前序、中序以及后序遍历2.1.1 前序遍历2.1.2 中序遍历、后序遍历2.2 题目练习2.2.1 求一棵二叉树的节点个数2.2.2 求一棵二叉树的叶节点个数2.2.3 求一棵二叉树第k层节点的个数2.2.4 求一棵二叉树的深度2.2.5 在一棵二叉树中查找…...

Oracle:递归树形结构查询功能
概要树状结构通常由根节点、父节点(PID)、子节点(ID)和叶节点组成。查询语法SELECT [LEVEL],* FROM table_name START WITH 条件1 CONNECT BY PRIOR 条件2 WHERE 条件3 ORDER BY 排序字段说明:LEVEL—伪列࿰…...

MongoDB数据库性能监控详解
目录一、MongoDB启动超慢1、启动日常卡住,根本不用为了截屏而快速操作,MongoDB启动真的超级慢~~2、启动MongoDB配置服务器,间歇性失败。3、查看MongoDB日志,分析“MongoDB启动慢”的原因。4、耗时“一小时”,MongoDB启…...

python不要再使用while死循环,使用定时器代替效果更佳!
在python开发的过程中,经常见到小伙伴直接使用while True的死循环sleep的方式来保存程序的一直运行。 这种方式虽然能达到效果,但是说不定什么时候就直接崩溃了。并且,在Linux环境中在检测到while True的未知进程就会直接干掉。 面对这样的…...
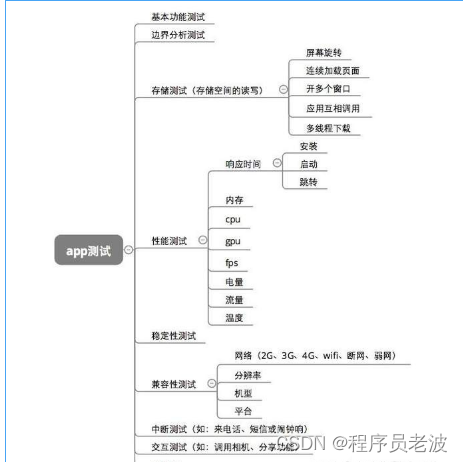
什么是接口测试?十年阿里测试人教你怎样做接口测试
一 什么是接口? 接口测试主要用于外部系统与系统之间以及内部各个子系统之间的交互点,定义特定的交互点,然后通过这些交互点来,通过一些特殊的规则也就是协议,来进行数据之间的交互。接口测试主要用于外部系统与系统之…...
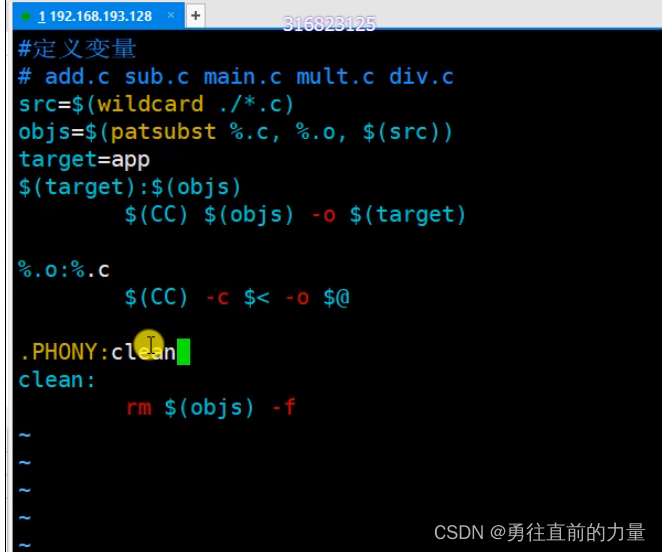
1.10-1.12 Makefile
1. Makefile简介 举个栗子,如下为redis-5.0.10的项目目录,有很多的文件 有了Makefile文件,可以简单的make一下就可以对项目文件进行编译,最终生成可执行程序。 2. Makefile栗子1 首先,创建vim Makefile按照PPT里的格…...
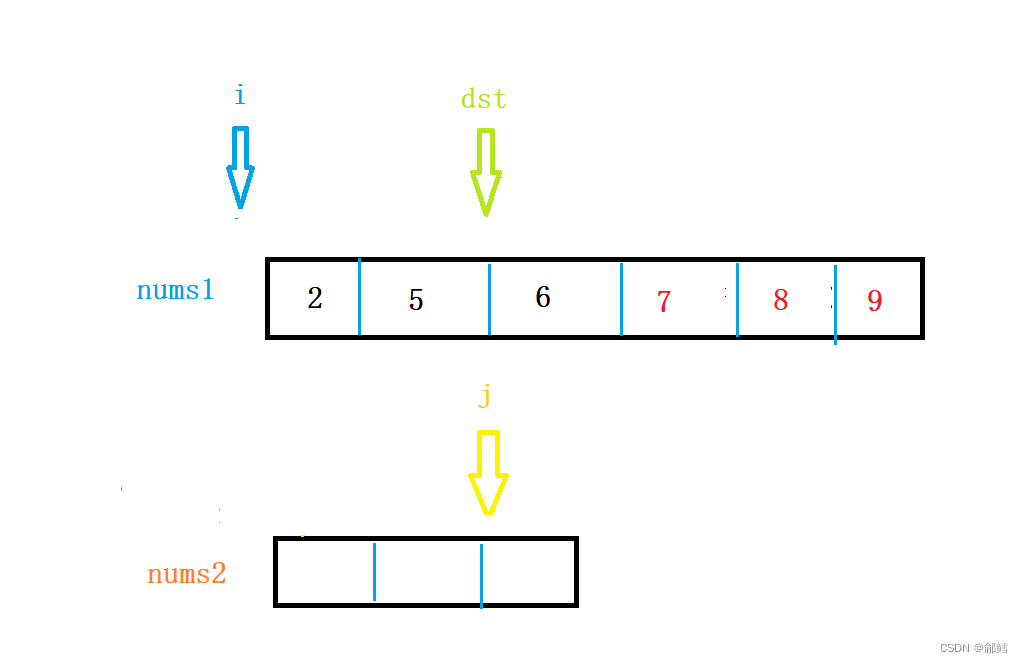
Leetcode. 88合并两个有序数组
合并两个有序数组 文章目录归并思路二归并 核心思路: 依次比较,取较小值放入新数组中 i 遍历nums1 , j 遍历nums2 ,取较小值放入nums3中 那如果nums[i] 和nums[j]中相等,随便放一个到nums3 那如果nums[i] 和nums[j]中相…...
【数据库】数据库查询(进阶命令详解)
目录 1.聚合查询 1.1聚合函数 COUNT函数 SUM函数 AVG函数 MAX函数 MIN函数 1.2GROUP BY子句 1.3HAVING 2.联合查询 2.1内连接 2.2外连接 2.3自连接 2.4子查询 3.合并查询 写在前面: 文章截图均是每个代码显示的图。数据库对代码大小写不敏感&am…...

参数缺省和函数重载讲解
一路风雨兼程磨砺意志,三载苦乐同享铸就辉煌 目录 1.参数缺省的概念 2.参数缺省的用法 3.缺省参数分类 3.1.全缺省参数 3.2.半缺省参数 4.函数重载的概念 5.函数重载的用法 6.函数重载的原理 1.参数缺省的概念 一般情况下,函数调用时的实参个数应…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...
