大话光学原理:1.“实体泛光说”、反射与折射
一、实体泛光说
在古希腊,那些喜好沉思的智者们中,曾流传着一个奇妙的设想:他们认为,我们的眼睛仿佛伸出无数触手般的光线,这些光线能向四面八方延伸,紧紧抓住周围的每一个物体。于是,当我们凝视某物时,实际上是我们的目光在轻抚着它。然而,这个理论很快就在先哲们严密的逻辑推理下土崩瓦解:如果我们的眼睛自带发光能力,那为何夜晚还会降临?如果我们不断从睁开眼皮的瞬间起,就不停地放射出光芒,黑暗又怎么可能存在?这个“眼睛发光论”自然不攻自破。尽管如此,关于光线如同触手的想象,却并没有因此消失无踪。

多年以后,一幅新的图景逐渐浮现,更具说服力地解释了我们的视觉奥秘:我们之所以能看见世界,是因为物体表面的微光悄悄穿透了我们的双眼。这一理论似乎在暗示,为了进入我们的视野,周围的石头、树木都在默默无闻地散发出光芒。每个生命,为了不被忽视,都必须努力闪耀自己的光芒。
这个新观点甚至试图解释黑暗的存在:只需所有生命和非生命同时停止发光,世界便会被黑暗笼罩。按照“实体泛光说”,虽然我们可以尝试创造一个小小的黑暗空间,但要抹去整个天空的光辉,其难度或许不亚于创造整个宇宙。那么,宇宙的创造者是否在每一粒物质背后都安装了一个秘密的亮度开关,以便绘制出无垠的夜空呢?
随着时间的流逝,工匠们手中的铜镜等光学工具日益精细,人类开始意识到,我们不仅可以用眼睛直接观察世界,还可以通过仪器从不同角度去探索。那些在阴影中清澈如水的镜片,一旦置于阳光下,便会闪耀出耀眼的光芒;在暗室中墙上凿开的小孔,竟能将屋外的景色倒映在对面墙上……这些奇妙的现象揭示了这样一个真理:视觉确实是外部光线激发视网膜产生的神经信号,但并非只有发光的物体才能被看见,那些不发光的物体同样可以通过周围的光线来展现自己的轮廓。所谓的黑暗,不过是光源暂时消失或被遮挡,使得不发光的物体显露出了它们本来的样子。
当我们似乎解开了“看”的谜题时,新的疑惑又随之而来:我们如何区分一个物体是在自发地“发光”,还是在借助周围的光线“借光”?光的本质究竟是什么呢?这些问题,依旧在人类的探索之中等待着答案。

二、反射与折射
当一束光在真空自由翱翔时,它毫无拘束地漫游着。然而,就在某个不经意的瞬间,一堵镜子突然出现在它的路径上。光勇敢地冲向前去,却惊讶地发现自己被温柔地弹了回来,这就是神奇的“反射”现象。带着些许好奇,光继续前行,这次却遇到了一汪清澈的泉水。它紧张地闭上眼睛,准备迎接新的挑战。不料——嘿,光竟然轻巧地穿过了这层界限,进入了一个全新的介质,并且改变了它的行进方向,这个过程被称作“折射”。
想象一下,在这两种介质的交界处,我们画一根垂直的线,这就是所谓的“法线”。光线与法线所形成的角度,就是我们所说的“入射角”。光线反射回来时与法线之间的角度,我们称之为“反射角”,而光线进入另一种介质后与法线形成的角度,则叫做“折射角”。这些角度之间隐藏着怎样的秘密联系呢?

人们观察到,不论是光线反射还是折射,其角度都会随着入射角的变化而相应调整。经过细致的测量,我们发现了一个简单而神奇的规律:在反射现象中,反射角总是与入射角保持一致。然而,折射现象则更为复杂。当光线穿越两种不同介质时,折射角虽然会有所偏移,但它始终与入射角保持同步增减。
那么,是什么神秘的力量决定了这个关键的比值呢?直到17世纪初,荷兰莱顿大学的数学教授威里布里德·斯涅耳通过整理多年的观测数据,终于揭示了这一规律:光线的偏转率取决于介质的搭配方式。这无疑是一项重大的发现。
举例来说,如果我们将光线的传播方向上下颠倒,让光线从水中进入真空,由于介质并未改变,我们只需将箭头翻转——原本的折射光变为入射光,而真空中的入射光变成折射光——就可以预测实际的情况。在这种情况下,入射角θi会比折射角θr更小,但折线的形状依然保持不变。
斯涅耳的这一发现,用数学语言表达,就是我们熟知的“折射定律”(斯涅尔定律)。

在光线的冒险中,θi和θr如同它的左右臂,分别指引着光线进入新领域的入射角与折射角。那个名为nr-i的神秘因子,则是连接两个世界的“相对折射率”。根据这一定律,我们只需将任意介质置于真空之中,测出光束从真空进入该介质的“绝对折射率”n,便可以预见到光的行踪。拿光从真空跃入水中的故事来说,我们已知它的绝对折射率为n水;而当光进入玻璃时,我们也知晓了它的绝对折射率n玻璃。借助斯涅耳定律,我们便能揭示光线接下来的旅程。

可推得:

相关文章:

大话光学原理:1.“实体泛光说”、反射与折射
一、实体泛光说 在古希腊,那些喜好沉思的智者们中,曾流传着一个奇妙的设想:他们认为,我们的眼睛仿佛伸出无数触手般的光线,这些光线能向四面八方延伸,紧紧抓住周围的每一个物体。于是,当我们凝视…...

住宅代理、移动代理和数据中心代理之间的区别
如果您是一名认真的互联网用户,可能需要反复访问某个网站或服务器,可能是为了数据抓取、价格比较、SEO 监控等用例,而不会被 IP 列入黑名单或被 CAPTCHA 阻止。 代理的工作原理是将所有传出数据发送到代理服务器,然后代理服务器将…...
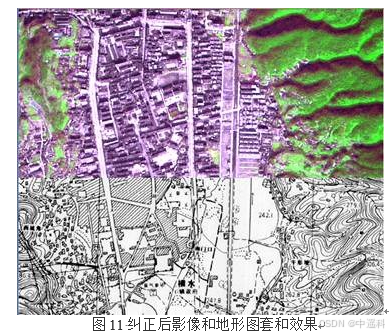
光学传感器图像处理流程(一)
光学传感器图像处理流程(一) 1. 处理流程总览2. 详细处理流程2.1. 图像预处理2.1.1. 降噪处理2.1.2. 薄云处理2.1.3. 阴影处理 2.2. 辐射校正2.2.1. 辐射定标2.2.2. 大气校正2.2.3. 地形校正 2.3. 几何校正2.3.1. 图像配准2.3.2. 几何粗校正2.3.3. 几何精…...

el-table 树状表格查询符合条件的数据
需要对el-table的树状表格根据输入机构名称,筛选出符合条件的数据,可用如下方法: 页面内容如下: <el-input v-model"ogeName" placeholder"请输入机构名称"><el-table :data"list" row…...
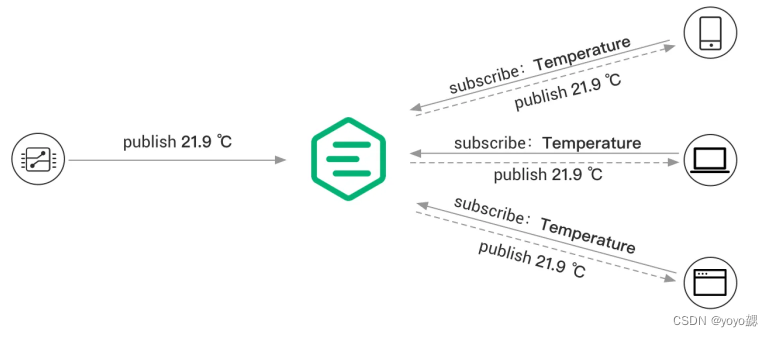
MQTT教程--服务器使用EMQX和客户端使用MQTTX
什么是MQTT MQTT(Message Queuing Telemetry Transport)是一种轻量级、基于发布-订阅模式的消息传输协议,适用于资源受限的设备和低带宽、高延迟或不稳定的网络环境。它在物联网应用中广受欢迎,能够实现传感器、执行器和其它设备…...

326. 3 的幂
哈喽!大家好,我是奇哥,一位专门给面试官添堵的职业面试员 文章持续更新,可以微信搜索【小奇JAVA面试】第一时间阅读,回复【资料】更有我为大家准备的福利哟! 文章目录 一、题目二、答案三、总结 一、题目 …...
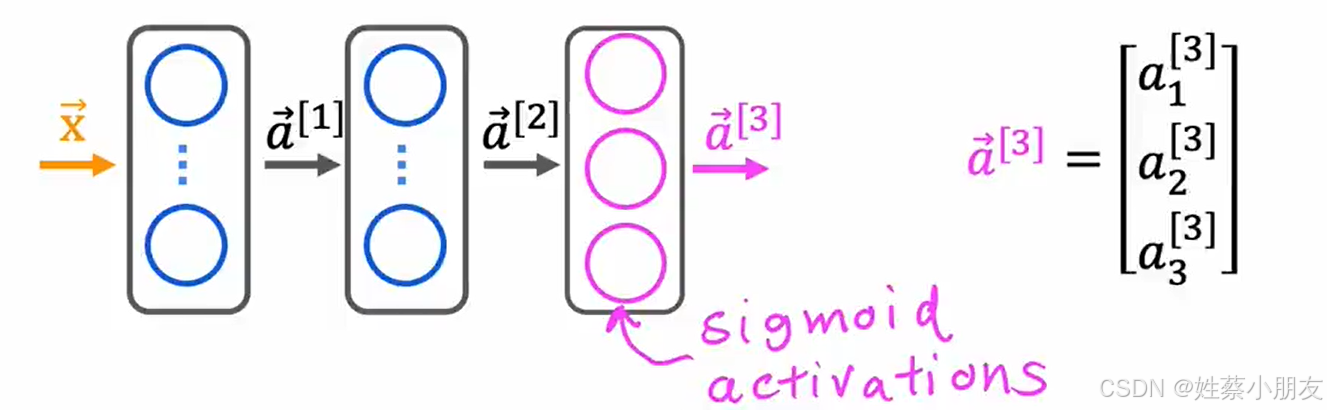
多标签问题
一、多标签问题与单标签问题的区别: 多标签问题是单标签问题的推广。 举个例子,同时识别图片中的小汽车,公交车,行人时,标签值有三个:小汽车,公交车,行人。 单标签问题仅对一个标签…...
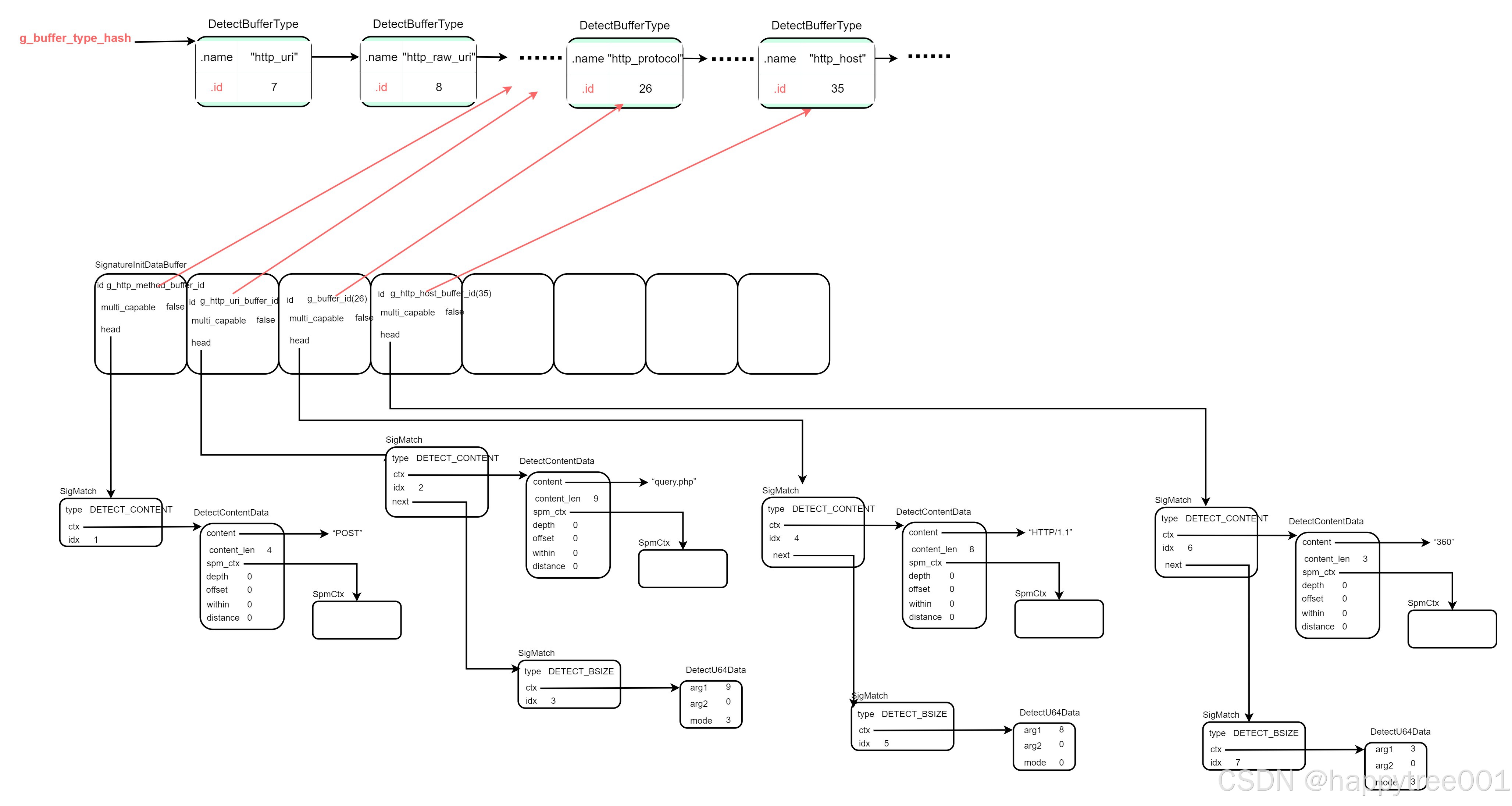
suricata7 rule加载(三)加载options
suricata7.0.5 加载options (msg:“HTTP Request Example”; flow:established,to_server; http.method; content:“POST”; http.uri; content:“query.php”; bsize:>9; http.protocol; content:“HTTP/1.1”; bsize:8; http.host; content:“360”; bsize:>3; class…...

【电路笔记】-C类放大器
C类放大器 文章目录 C类放大器1、概述2、C类放大介绍3、C类放大器的功能4、C 类放大器的效率5、C类放大器的应用:倍频器6、总结1、概述 尽管存在差异,但我们在之前有关 A 类、B 类和 AB 类放大器的文章中已经看到,这三类放大器是线性或部分线性的,因为它们在放大过程中再现…...

c++语法之函数重载
引例 我们在C语言里面写add函数的时候,只能支持一种类型的相加,除非我们创建多个add函数: 但是这样写并不方便,于是就有了c的函数重载。 函数重载 函数重载就是可以将多个参数类型、顺序、数量不同,实现逻辑相同的函…...

EtherCAT主站IGH-- 11 -- IGH之fmmu_config.h/c文件解析
EtherCAT主站IGH-- 11 -- IGH之fmmu_config.h/c文件解析 0 预览一 该文件功能`fmmu_config.c` 文件功能函数预览二 函数功能介绍1. `ec_fmmu_config_init`2. `ec_fmmu_set_domain_offset_size`3. `ec_fmmu_config_page`示例用法示例详细说明三 h文件翻译四 c文件翻译该文档修改…...
如何使用IDEA快速清理无效代码(荣耀典藏版)
大家好,我是月夜枫。 今天分享一下IDEA中很有实用价值的Analyze,那么Analyze是用来做什么的呢? 主要用来清理没有引用的代码,包括方法、实体类以及没有使用的Mapper和Service等。 为了是项目更加整洁,可以使用Idea中…...
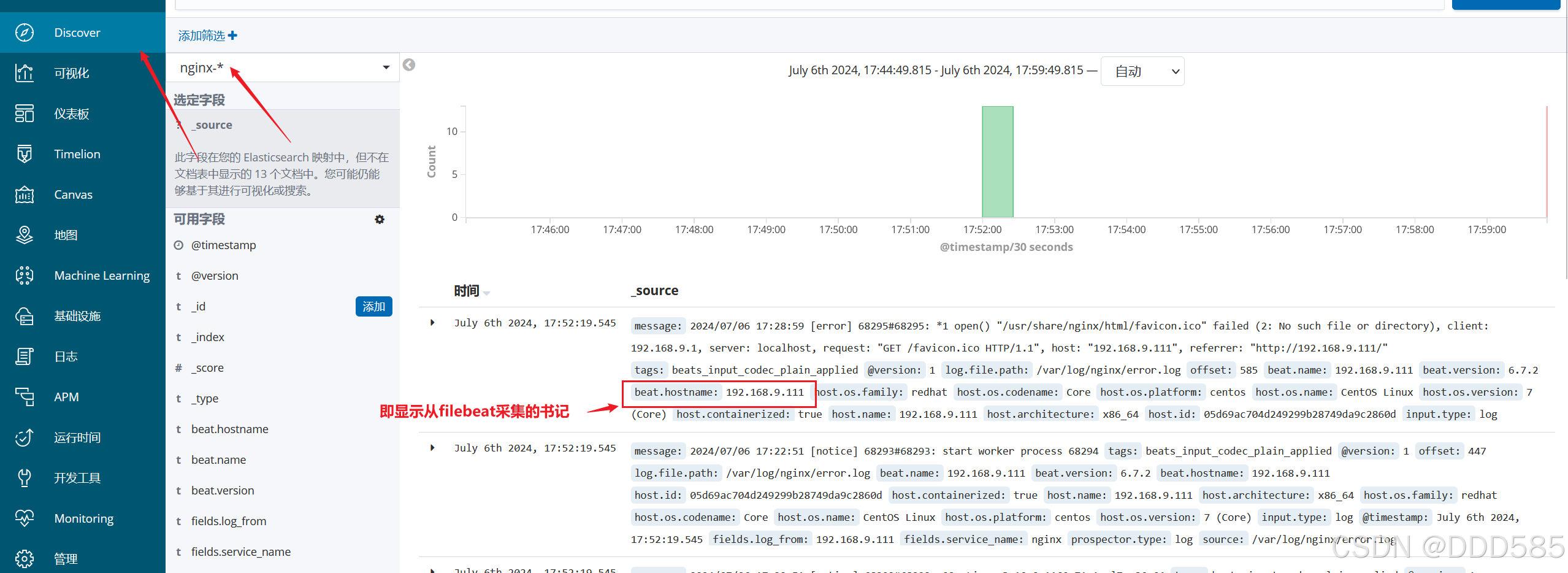
ELK优化之Filebeat部署
目录 1.安装配置Nginx 2.安装 Filebeat 3.设置 filebeat 的主配置文件 4.修改Logstash配置 5.启动配置 6.kibana验证 主机名ip地址主要软件es01192.168.9.114ElasticSearches02192.168.9.115ElasticSearches03192.168.9.116ElasticSearch、Kibananginx01192.168.9.113ng…...
及其Python和MATLAB实现)
蝙蝠优化算法(Bat Algorithm,BA)及其Python和MATLAB实现
蝙蝠优化算法(Bat Algorithm,简称BA)是一种基于蝙蝠群体行为的启发式优化算法,由Xin-She Yang于2010年提出。该算法模拟了蝙蝠捕食时在探测目标、适应环境和调整自身位置等过程中的行为,通过改进搜索过程来实现优化问题…...

vscode运行java中文乱码,引发的mac配置问题
文章目录 问题 vscode 安装 java环境之后 public class Main{ public static void main(String[] args) { System.out.println(“哈哈”); } } ➜ .leetcode cd “/Users/leesin/.leetcode/.vscode/” && javac -encoding utf-8 Main.java && java Main &am…...
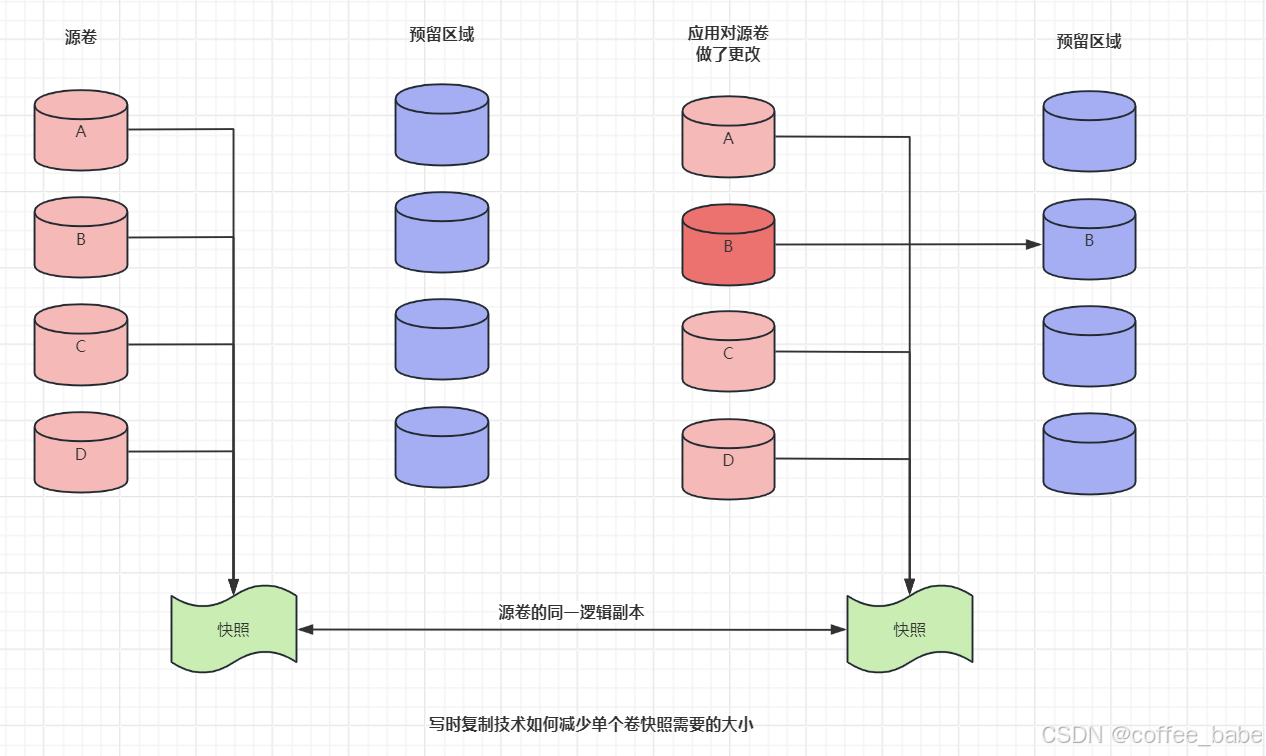
MySQL之备份与恢复(五)
备份与恢复 备份数据 符号分隔文件备份 可以使用SQL命令SELECT INTO OUTFILE以符号分隔文件格式创建数据的逻辑备份。(可以用mysqldump的 --tab选项导出到符号分隔文件中)。符号分隔文件包含以ASCII展示的原始数据,没有SQL、注释和列名。下面是一个导出为逗号分隔…...

离线运行Llama3:本地部署终极指南_liama2 本地部署
4月18日,Meta在官方博客官宣了Llama3,标志着人工智能领域迈向了一个重要的飞跃。经过笔者的个人体验,Llama3 8B效果已经超越GPT-3.5,最为重要的是,Llama3是开源的,我们可以自己部署! 本文和大家…...

【YOLO8系列】(二)YOLOv8环境配置,手把手嘴对嘴保姆教学
目录 一. 准备环境 1.Anaconda下载 2.创建yolov8虚拟环境 3.pytorch安装 4.CUDA下载 5.CUDNN下载 二、yolov8模型下载 1.clone模型 2.pycharm配置 ①解释器配置 ②终端配置 3.安装必要库 4.下载训练模型 三、 环境验证 四、总结 YOLOv8 是 YOLO 系列最新的目标…...
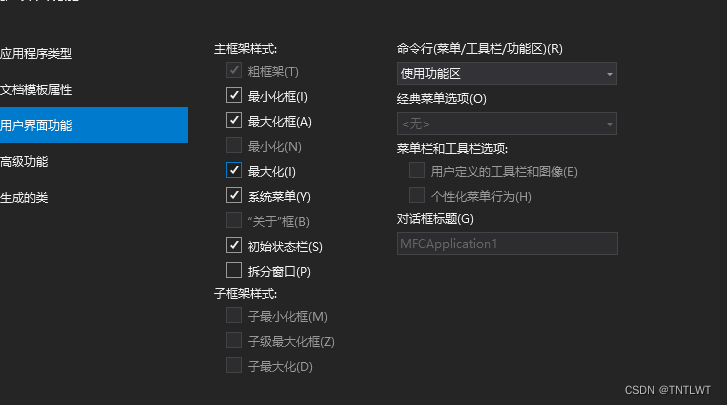
MFC常见问题解决
文章目录 1. 单文档程序初始化显示设置问题解决方案 2. MFC中控件响应出错 1. 单文档程序初始化显示设置 问题 在Microsoft Foundation Classes (MFC) 中,单文档应用程序(SDI)的初始化时默认并不设置为最大显示。但你可以通过编程方式在程序…...
学生管理系统 | python
1. 题目描述 ****************************** 欢迎使用学生管理系统 ****************************** 1. 添加学生 2. 查看学生列表 3. 查看学生信息 4. 删除学生 5. 退出系统 1 请输入学生姓名: zhangsan 请输入学生学号: 10010 请输入学生班级: 3 请输入学生成…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

tomcat入门
1 tomcat 是什么 apache开发的web服务器可以为java web程序提供运行环境tomcat是一款高效,稳定,易于使用的web服务器tomcathttp服务器Servlet服务器 2 tomcat 目录介绍 -bin #存放tomcat的脚本 -conf #存放tomcat的配置文件 ---catalina.policy #to…...

解析奥地利 XARION激光超声检测系统:无膜光学麦克风 + 无耦合剂的技术协同优势及多元应用
在工业制造领域,无损检测(NDT)的精度与效率直接影响产品质量与生产安全。奥地利 XARION开发的激光超声精密检测系统,以非接触式光学麦克风技术为核心,打破传统检测瓶颈,为半导体、航空航天、汽车制造等行业提供了高灵敏…...

图解JavaScript原型:原型链及其分析 | JavaScript图解
忽略该图的细节(如内存地址值没有用二进制) 以下是对该图进一步的理解和总结 1. JS 对象概念的辨析 对象是什么:保存在堆中一块区域,同时在栈中有一块区域保存其在堆中的地址(也就是我们通常说的该变量指向谁&…...

简单介绍C++中 string与wstring
在C中,string和wstring是两种用于处理不同字符编码的字符串类型,分别基于char和wchar_t字符类型。以下是它们的详细说明和对比: 1. 基础定义 string 类型:std::string 字符类型:char(通常为8位)…...
未授权访问事件频发,我们应当如何应对?
在当下,数据已成为企业和组织的核心资产,是推动业务发展、决策制定以及创新的关键驱动力。然而,未授权访问这一隐匿的安全威胁,正如同高悬的达摩克利斯之剑,时刻威胁着数据的安全,一旦触发,便可…...

基于小程序老人监护管理系统源码数据库文档
摘 要 近年来,随着我国人口老龄化问题日益严重,独居和居住养老机构的的老年人数量越来越多。而随着老年人数量的逐步增长,随之而来的是日益突出的老年人问题,尤其是老年人的健康问题,尤其是老年人产生健康问题后&…...
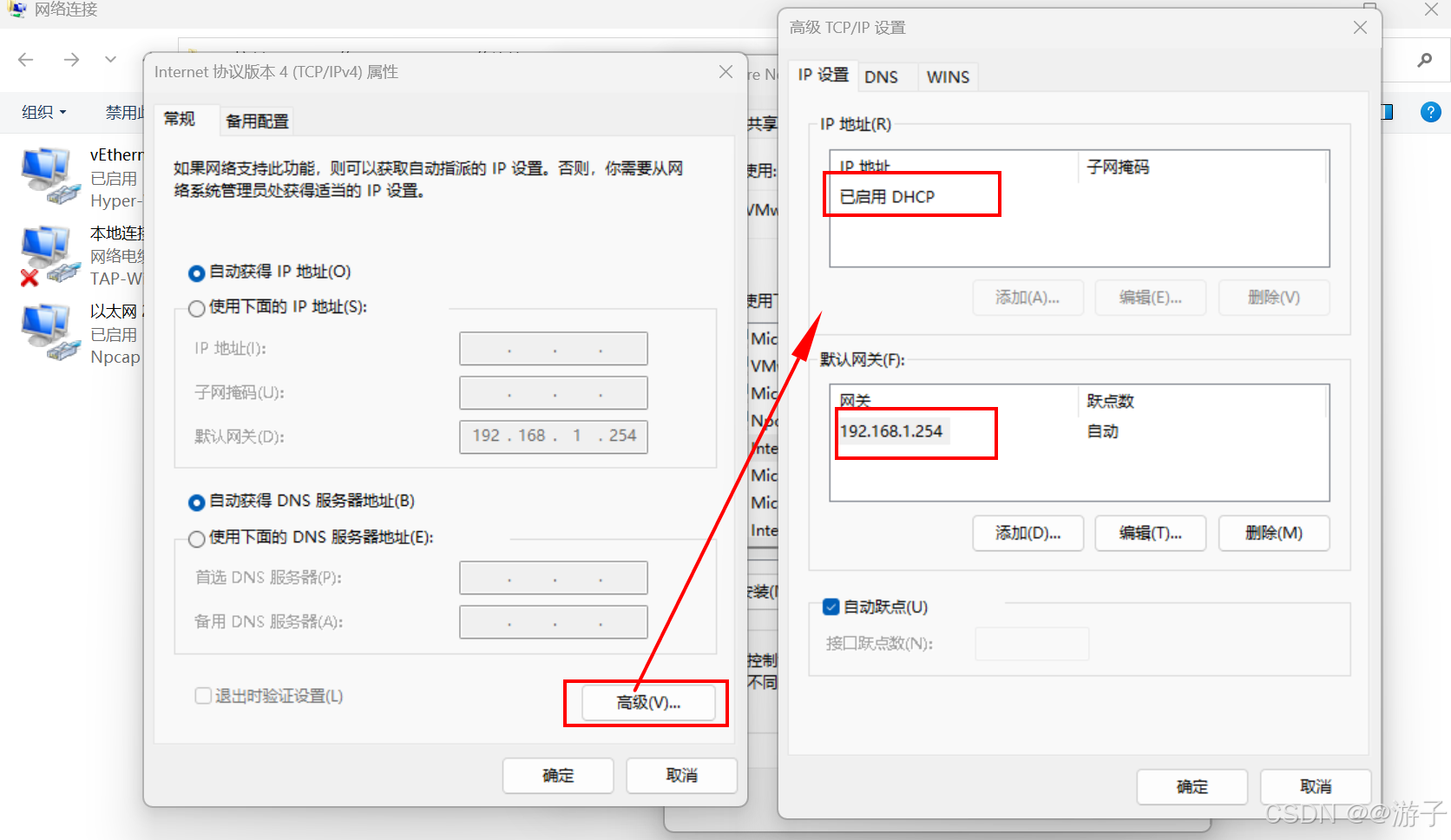
虚拟机网络不通的问题(这里以win10的问题为主,模式NAT)
当我们网关配置好了,DNS也配置好了,最后在虚拟机里还是无法访问百度的网址。 第一种情况: 我们先考虑一下,网关的IP是否和虚拟机编辑器里的IP一样不,如果不一样需要更改一下,因为我们访问百度需要从物理机…...

AWSLambda之设置时区
目标 希望Lambda运行的时区是东八区。 解决 只需要设置lambda的环境变量TZ为东八区时区即可,即Asia/Shanghai。 参考 使用 Lambda 环境变量...
