实变函数精解【3】
文章目录
- 点集
- 求导集
- 闭集
- 参考文献
点集
求导集
- 例1
E = { 1 / n + 1 / m : n , m ∈ N } 1. lim n → ∞ ( 1 / n + 1 / m ) = 1 / m 2. lim n , m → ∞ ( 1 / n + 1 / m ) = 0 3. E ′ = { 0 , 1 , 1 / 2 , 1 / 3 , . . . . } E=\{1/n+1/m:n,m \in N\} \\1.\lim_{n \rightarrow \infty}(1/n+1/m)=1/m \\2.\lim_{n,m \rightarrow \infty}(1/n+1/m)=0 \\3.E'=\{0,1,1/2,1/3,....\} E={1/n+1/m:n,m∈N}1.n→∞lim(1/n+1/m)=1/m2.n,m→∞lim(1/n+1/m)=03.E′={0,1,1/2,1/3,....} - 例2
E = { ( m − n ) / ( m + n ) : m , n ∈ N } 1. ( m − n ) / ( m + n ) = 1 − 2 m n + 1 2. lim n → ∞ ( 1 − 2 m n + 1 ) = − 1 3. lim m → ∞ ( 1 − 2 m n + 1 ) = 1 4. lim n , m → ∞ ( 1 − 2 m n + 1 ) = lim n , m → ∞ ( 1 − 1 2 1 m n + 1 ) 1 m n + 1 < 1 = > − 1 < lim n , m → ∞ ( 1 − 1 2 1 m n + 1 ) < 1 E ′ = [ − 1 , 1 ] E=\{(\sqrt m-\sqrt n)/(\sqrt m +\sqrt n):m,n \in N\} \\1.(\sqrt m-\sqrt n)/(\sqrt m +\sqrt n)=1-\frac {2} {\sqrt {m \over n}+1} \\2.\lim_{n \rightarrow \infty }(1-\frac {2} {\sqrt {m \over n}+1})=-1 \\3.\lim_{m \rightarrow \infty }(1-\frac {2} {\sqrt {m \over n}+1})=1 \\4.\lim_{n,m \rightarrow \infty }(1-\frac {2} {\sqrt {m \over n}+1})=\lim_{n,m \rightarrow \infty }(1- \frac 1 2 \frac {1} {\sqrt {m \over n}+1}) \\\frac {1} {\sqrt {m \over n}+1} < 1=> \\-1 <\lim_{n,m \rightarrow \infty }(1- \frac 1 2 \frac {1} {\sqrt {m \over n}+1})<1 \\E'=[-1,1] E={(m−n)/(m+n):m,n∈N}1.(m−n)/(m+n)=1−nm+122.n→∞lim(1−nm+12)=−13.m→∞lim(1−nm+12)=14.n,m→∞lim(1−nm+12)=n,m→∞lim(1−21nm+11)nm+11<1=>−1<n,m→∞lim(1−21nm+11)<1E′=[−1,1] - 例3
E = { x n = s i n l n n : n ∈ N } E=\{x_n=sinlnn:n \in N\} E={xn=sinlnn:n∈N}

lim n → ∞ l n n = ∞ − 1 ≤ lim n → ∞ s i n l n n ≤ 1 E ′ = [ − 1 , 1 ] \lim_{n \rightarrow \infty}lnn=\infty \\-1\le \lim_{n \rightarrow \infty}sinlnn \le1 \\E'=[-1,1] n→∞limlnn=∞−1≤n→∞limsinlnn≤1E′=[−1,1]
闭集
E ⊂ R n , E ⊃ E ′ = > E 为闭集 E \subset R^n,E \supset E'=>E为闭集 E⊂Rn,E⊃E′=>E为闭集
E ˉ = E ∪ E ′ = > E 为闭包 \bar E=E \cup E'=>E为闭包 Eˉ=E∪E′=>E为闭包
A ⊂ B , A ˉ = B = > A 在 B 中稠密 , A 是 B 的稠密子集 A \subset B,\bar A=B=>A在B中稠密,A是B的稠密子集 A⊂B,Aˉ=B=>A在B中稠密,A是B的稠密子集
下面内容由文心一言生成
在实变函数中,闭集是一个重要的概念,它与开集相对。以下是对实变函数中闭集的详细解释:
定义:
- 在实数集R(或更一般的度量空间、拓扑空间)中,闭集是指包含其所有极限点的集合。
- 换句话说,如果一个集合的所有极限点都属于该集合本身,则它是闭集。
性质:
- 闭集在并集、交集和补集运算下具有良好的性质。
- 任意多个闭集的交集仍然是闭集。
- 有限个闭集的并集也是闭集。
- 闭集的补集是开集(在实数集R中)。
例子:
- 在实数集R中,闭区间[a, b]是一个闭集,因为它包含了其所有边界点a和b,以及区间内的所有点。
- 单点集{x}也是一个闭集,因为它只包含一个点,该点自然是它自己的极限点。
- 空集∅也是一个闭集,因为它不包含任何点,所以也没有极限点需要包含。
与开集的关系:
- 开集和闭集是相对的。一个集合是开集当且仅当它的补集是闭集。
- 在实数集R中,开区间(a, b)是一个开集,而它的补集是闭集,由两个闭区间和两个单点集组成:(-∞, a] ∪ [b, +∞) ∪ {a} ∪ {b}(但通常我们只说它的补集包含(-∞, a]和[b, +∞)这两部分,因为单点集在实数轴上可视为闭集)。
闭包与闭集的关系:
- 任何一个集合S的闭包都是闭集。
- 闭包是包含S的最小闭集,即S的闭包是包含S的所有闭集中的最小者(在包含关系下)。
综上所述,闭集是实变函数中一个基本而重要的概念,它与开集、闭包等概念紧密相关,并在数学分析中发挥着重要作用。
在点集拓扑学中,对于实数集R(或更一般的度量空间、拓扑空间)中的一个点集E,E的闭包通常定义为E与E的所有极限点(或聚点)的并集,记作Ē或E∪E′。这里,E′表示E的导集,即E中所有聚点的集合。聚点的定义是:对于E中的点x,如果存在一个包含x的邻域U,使得U与E的交集(去掉x后)非空,则称x为E的聚点。
性质:闭包是包含原集合的最小闭集。即,对于任意集合E,其闭包Ē是包含E的所有闭集中最小的一个。 例子:考虑实数集R上的开区间(0,1),其闭包是闭区间[0,1],因为0和1是(0,1)的聚点。
参考文献
1.《实变函数解题指南》 周民强
2.《实变函数论》 周民强
相关文章:

实变函数精解【3】
文章目录 点集求导集 闭集参考文献 点集 求导集 例1 E { 1 / n 1 / m : n , m ∈ N } 1. lim n → ∞ ( 1 / n 1 / m ) 1 / m 2. lim n , m → ∞ ( 1 / n 1 / m ) 0 3. E ′ { 0 , 1 , 1 / 2 , 1 / 3 , . . . . } E\{1/n1/m:n,m \in N\} \\1.\lim_{n \rightar…...

JVM:SpringBoot TomcatEmbeddedWebappClassLoader
文章目录 一、介绍二、SpringBoot中TomcatEmbeddedWebappClassLoader与LaunchedURLClassLoader的关系 一、介绍 TomcatEmbeddedWebappClassLoader 是 Spring Boot 在其内嵌 Tomcat 容器中使用的一个类加载器(ClassLoader)。在 Spring Boot 应用中&#…...
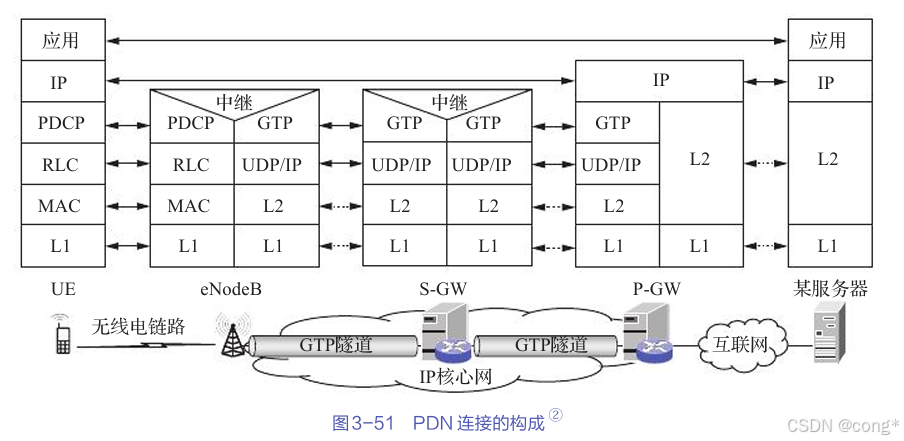
蜂窝互联网接入:连接世界的无缝体验
通过Wi—Fi,人们可以方便地接入互联网,但无线局域网的覆盖范围通常只有10~100m。当我们携带笔记本电脑在外面四处移动时,并不是在所有地方都能找到可接入互联网的Wi—Fi热点,这时候蜂窝移动通信系统可以为我们提供广域…...

Sprint Boot 2 核心功能(一)
核心功能 1、配置文件 application.properties 同基础入门篇的application.properties用法一样 Spring Boot 2 入门基础 application.yaml(或application.yml) 基本语法 key: value;kv之间有空格大小写敏感使用缩进表示层级关系缩进不允…...
GitLab CI/CD实现项目自动化部署
1 GitLab CI/CD介绍 GitLab CI/CD 是 GitLab 中集成的一套用于软件开发的持续集成(Continuous Integration)、持续交付(Continuous Delivery)和持续部署(Continuous Deployment)工具。这套系统允许开发团队…...

阿里云调整全球布局关停澳洲云服务器,澳洲服务器市场如何选择稳定可靠的云服务?
近日,阿里云宣布将关停澳大利亚地域的数据中心服务,这一决定引发了全球云计算行业的广泛关注。作为阿里云的重要海外市场之一,澳洲的数据中心下架对于当地的企业和个人用户来说无疑是一个不小的挑战。那么,在阿里云调整全球布局的…...
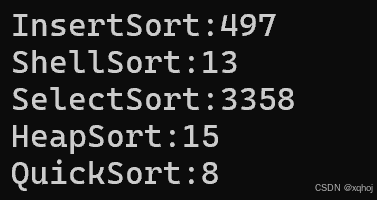
排序(二)——快速排序(QuickSort)
欢迎来到繁星的CSDN,本期内容包括快速排序(QuickSort)的递归版本和非递归版本以及优化。 一、快速排序的来历 快速排序又称Hoare排序,由霍尔 (Sir Charles Antony Richard Hoare) ,一位英国计算机科学家发明。霍尔本人是在发现冒泡排序不够快…...
<数据集>穿越火线cf人物识别数据集<目标检测>
数据集格式:VOCYOLO格式 图片数量:3440张 标注数量(xml文件个数):3440 标注数量(txt文件个数):3440 标注类别数:1 标注类别名称:[person] 使用标注工具:labelImg 标注规则:对…...

a+=1和a=a+1的区别
文章目录 a1 和a a1的区别一、实例代码二、代码解释三、总结 a1 和a a1的区别 一、实例代码 public class Test {public static void main(String[] args) {byte a 10; // a a 1; // a (byte) (a 1);a 1;System.out.println(a);} }上面的对变量a进行加一操作时&a…...
)
设计模式使用场景实现示例及优缺点(结构型模式——桥接模式)
结构型模式 桥接模式(Bridge Pattern) 桥接模式(Bridge Pattern)是一种结构型设计模式,其主要目的是“将抽象与实现解耦,使得两者可以独立地变化”。这种模式通过提供抽象化和实现化之间的桥接结构&#…...

Spring——自动装配Bean
自动装配是Spring满足bean依赖的一种方式 Spring会在上下文中自动寻找,并自动给bean装配属性 在Spring中有三种装配的方式: 1. 在xml中显示配置 2. 在java中显示配置 3. 隐式的自动装配bean【重要】 测试 记得创建Cat、Dog、People类 public clas…...

云端典藏:iCloud中个人收藏品目录的智能存储方案
云端典藏:iCloud中个人收藏品目录的智能存储方案 在数字化生活不断推进的今天,个人收藏品的管理也趋向于电子化和云端化。iCloud作为苹果公司提供的云服务,为个人收藏品目录的存储和管理提供了一个安全、便捷、跨设备的解决方案。本文将详细…...

安全开发基础篇-数据溢出
上一节我们简单讲解了多语言的数据类型,我们只需要知道这个概念,并且在不同语言有不同的规矩就好。这节讲数据溢出,严格说应该是字符串溢出和整数溢出。 在软件开发中,字符串和整数溢出漏洞是常见的安全问题,它们可能…...

Scanner工具类
扫描控制台输入 1.nextLine nextLine() 方法会扫描输入流中的字符,直到遇到行末尾的换行符 \n,然后将该行的内容作为字符串返回,同时,nextLine() 会将 Scanner 对象的位置移动到下一行的开头,以便下一次读取数据时从下…...

springboot3 集成GraalVM
目录 安装GraalVM 配置环境变量 Pom.xml 配置 build包 测试 安装GraalVM Download GraalVM 版本和JDK需要自己选择 配置环境变量 Jave_home 和 path 设置setting.xml <profile><id>graalvm-ce-dev</id><repositories><repository><id&…...
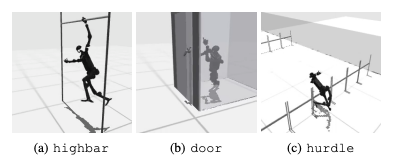
HumanoidBench——模拟仿人机器人算法有未来
概述 论文地址:https://arxiv.org/pdf/2403.10506 仿人机器人具有类似人类的外形,有望在各种环境和任务中为人类提供支持。然而,昂贵且易碎的硬件是这项研究面临的挑战。因此,本研究开发了使用先进模拟技术的 HumanoidBench。该基…...
)
实现前端用户密码重置功能(有源码)
引言 密码重置功能是任何Web应用程序中至关重要的一部分。当用户忘记密码时,密码重置功能可以帮助他们安全地重设密码。本文将介绍如何使用HTML、CSS和JavaScript(包括Vue.js)来实现前端的密码重置功能。 1. 项目结构 首先,我们…...

《双流多依赖图神经网络实现精确的癌症生存分析》| 文献速递-基于深度学习的多模态数据分析与生存分析
Title 题目 Dual-stream multi-dependency graph neural network enables precise cancer survival analysis 《双流多依赖图神经网络实现精确的癌症生存分析》 01 文献速递介绍 癌症是全球主要的死亡原因,2020年约有1930万新发癌症病例和近1000万癌症相关死亡…...

【Hive SQL 每日一题】在线峰值人数计算
文章目录 测试数据需求说明需求实现 测试数据 -- 创建 user_activity 表 DROP TABLE IF EXISTS user_activity ; CREATE TABLE user_activity (user_id STRING,activity_start TIMESTAMP,activity_end TIMESTAMP );-- 插入数据 INSERT INTO user_activity VALUES (user1, 2024…...

谷粒商城学习笔记-18-快速开发-配置测试微服务基本CRUD功能
文章目录 一,product模块整合mybatis-plus1,引入依赖2,product启动类指定mapper所在包3,在配置文件配置数据库连接信息4,在配置文件中配置mapper.xml映射文件信息 二,单元测试1,编写测试代码&am…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

Proxmox Mail Gateway安装指南:从零开始配置高效邮件过滤系统
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:「storms…...

给网站添加live2d看板娘
给网站添加live2d看板娘 参考文献: stevenjoezhang/live2d-widget: 把萌萌哒的看板娘抱回家 (ノ≧∇≦)ノ | Live2D widget for web platformEikanya/Live2d-model: Live2d model collectionzenghongtu/live2d-model-assets 前言 网站环境如下,文章也主…...

破解路内监管盲区:免布线低位视频桩重塑停车管理新标准
城市路内停车管理常因行道树遮挡、高位设备盲区等问题,导致车牌识别率低、逃费率高,传统模式在复杂路段束手无策。免布线低位视频桩凭借超低视角部署与智能算法,正成为破局关键。该设备安装于车位侧方0.5-0.7米高度,直接规避树枝遮…...

xmind转换为markdown
文章目录 解锁思维导图新姿势:将XMind转为结构化Markdown 一、认识Xmind结构二、核心转换流程详解1.解压XMind文件(ZIP处理)2.解析JSON数据结构3:递归转换树形结构4:Markdown层级生成逻辑 三、完整代码 解锁思维导图新…...
32单片机——基本定时器
STM32F103有众多的定时器,其中包括2个基本定时器(TIM6和TIM7)、4个通用定时器(TIM2~TIM5)、2个高级控制定时器(TIM1和TIM8),这些定时器彼此完全独立,不共享任何资源 1、定…...
