MICCAI 2024Centerline Boundary Dice Loss for Vascular Segmentation
MICCAI 2024 Centerline Boundary Dice Loss for Vascular Segmentation
- MICCAI 2024Centerline Boundary Dice Loss for Vascular Segmentation
- 中心线边界Dice损失用于血管分割
- **摘要**:
- 1. 引言
- 相关工作:
- 2. 方法
- 预备知识
- Dice的变化
- 3 实验
- 3.1 数据集
- 3.2 设置
- 3.3 结果
- 4 结论
- 5. 补充材料
MICCAI 2024Centerline Boundary Dice Loss for Vascular Segmentation
中心线边界Dice损失用于血管分割
彭成世1, 捷斯·胡1,2, 颜武洋1,2, 齐乐高1, 韦磊1, 马霆1,2,3,4
- 哈尔滨工业大学(深圳)电子与信息工程学院,深圳,中国
- 彭程实验室,深圳,中国
- 哈尔滨工业大学(深圳)通信与网络技术省重点实验室,深圳,中国
- 哈尔滨工业大学(深圳)人工智能研究院,深圳,中国
邮箱:tma@hit.edu.cn
摘要:
在医学成像中,血管分割在形态学和功能评估中起着至关重要的作用。传统方法,如中心线Dice (clDice) 损失,确保拓扑保留但在捕获几何细节(特别是平移和变形)方面存在缺陷。结合传统Dice损失的clDice可以导致直径不平衡,偏向较大的血管。为了解决这些挑战,我们引入了中心线边界Dice (cbDice) 损失函数,该函数保持拓扑完整性和几何统一性,确保跨各种血管尺度的一致分割。cbDice通过包括边界感知方面丰富了clDice,从而提高了几何细节捕获能力。它通过基于掩膜距离的方法实现了与边界差异(B-Dou)损失相当的性能,增强了平移灵敏度。关键的是,cbDice从血管骨架中整合信息,使直径变化均匀,并在分支处保持一致影响。此外,我们进行了各类Dice变体的理论分析(t-X-Dice)。我们验证了cbDice在二维和三维、多尺度分割应用中的有效性。特别是在多分支情况下,使用cbDice的方法在近期的MICHAL 2023分割挑战中取得了卓越表现。我们的代码已公开可用,地址为: https://github.com/PengchengShi1220/cbDice.
关键词: 血管分割, 中心线边界损失, 直径平衡
1. 引言
深度学习的进步显著提升了医学图像分割的能力,尤其是在血管方面,革新了诊断和介入放射学。然而,现有的评估指标常常忽视特定领域的要求,如几何细节的不足【10,15】。血管分割遇到的特定挑战包括:1) 保持拓扑完整性;2) 精确的几何分割(如准确的血液动力学分析);3) 基于解剖学的血管网络标记(如处理静脉窦);4) 跨不同血管直径的一致分割并随着几何变化进行直径调整(见图1)。
在本文中,我们寻求解决一个基本问题:如何在血管分割中实现拓扑和几何一致性?近期在深度学习驱动的血管分割领域的重大进展得益于利用生物学知识【4,13,20,17,11,7,14,2】和几何知识【24,13,23,12,18,14】的网络方法。然而,在医学图像分割中设计损失函数以减轻数据不平衡方面的进展有限【6,28,27】。一个全面的分析框架在这一领域仍然缺乏。我们的研究旨在通过提出中心线边界Dice (cbDice)损失函数来弥补这一差距。cbDice独特地结合了从血管骨架中提取的半径信息。这种方法促进了不同直径血管的一致分割,关键地保持了拓扑一致性。我们的贡献如下:(1)我们介绍了统一的clX-Dice变体,一个结合拓扑完整性和血管直径一致性的血管分割框架。(2) 从中心线Dice (clDice)损失中引入几何考虑因素,等效于边界差异过联合 (B-Dou)损失的新方法,使用基于掩膜距离的方法,增强了平移敏感性。(3) 我们提出了cbDice通过整合来自血管骨架的信息,适应血管直径的变化,确保分支的一致影响。(4) 我们进行了一般理论分析,以展示不同clX-Dice实现的几何变换响应。 除此之外,我们还验证了cbDice在各种血管分割数据集中的有效性,包括二维和三维,以及二元和多类分割任务。
相关工作:
(i) 拓扑学: 保持连接性,如使用非监督的持续同调【4,13,20】,中心线或骨架化技术【11,17】和欧拉特征方法【7】,至关重要。拓扑不变性确保了在平移和变形情况下的几何细节保持。例如,clDice损失函数【17】强调了在捕获几何精度时保持拓扑完整性,但在捕获几何精度(尤其是平移和变形)方面存在不足。这凸显了需要能够和谐平衡拓扑保真度与精准几何表示的分割方法。
(ii) 几何学: 最近的工作通过如B-Dou损失【8】和深度编码网络【24】等方法突出了几何性的重要性。技术如动态形状卷积【13】和特征传递【21】在医学图像分割中得到了应用。基于距离图的方法变得普遍,包括使用带符号距离图的形状感知分割【25】,以及基于距离变换图的CNN集成【9】。最近的技术结合了中心线和距离图,展示了在管状结构分割中同时约束骨架和几何形态的能力【23,18】。然而,它们在损失函数中的综合集成不足,这对于扩大适用性和泛化性至关重要。尽管基于clDice的归一化骨架距离变换(NSDT)损失【14】在几何形态和拓扑保真度方面表现出色,传统的损失函数如Dice损失仍然受到直径不平衡的影响。
(iii) 不平衡: 在医学图像分割中,不平衡是一个常见问题,传统的Dice损失在较大解剖结构上表现出偏差。为了解决这个问题,最近的研究提出了一系列针对不平衡解决方案,包括边界损失【6】、局部Dice损失【28】、联合损失【22】和统一焦点损失【27】。这些方法旨在减轻不平衡分割。然而,它们并未特别解决血管网络中直径不平衡的问题,同时忽视了血管网络的连接性。
2. 方法
预备知识
该方法首先通过模型处理输入 X ∈ R c i i m e s N X \in \mathbb{R}^{c_i imes N} X∈RciimesN ,生成输出 Y ∈ R c o i m e s N Y \in \mathbb{R}^{c_o imes N} Y∈RcoimesN ,其中 c i c_i ci 和 c o c_o co 分别表示输入和输出通道的数量。随后,输出 Y Y Y 被转换为二值掩码,记为 V V V 。这里, N N N 表示像素或体素的总数,定义为 w i m e s h w imes h wimesh 对于2D图像,或 w i m e s h i m e s d w imes h imes d wimeshimesd 对于3D体积,其中 w , h , d w, h, d w,h,d 分别表示宽度、高度和深度。掩码 V V V 定义为 V = { v i ; b j ∣ i ∈ [ 1 , q ] , j ∈ [ 1 , k ] } ,包括值为 1 的掩码点( V = \{v_i; b_j | i \in [1,q], j \in [1,k]\} ,包括值为1的掩码点( V={vi;bj∣i∈[1,q],j∈[1,k]},包括值为1的掩码点(v$)和值为0的背景点( b b b )。相应的骨架 S S S 由 V V V 导出,组成 S = { s i ; b j s ∣ i ∈ [ 1 , n ] , j ∈ [ 1 , m ] } S = \{s_i; b_j^s | i \in [1,n], j \in [1,m]\} S={si;bjs∣i∈[1,n],j∈[1,m]} ,其中 n n n 个骨架点( s s s )值为1, m m m 个背景点( b s b^s bs )值为0。 V V V 和 S S S 都属于 R N \mathbb{R}^N RN 。下标 P 和 L 分别表示预测和参考。我们从检查传统的 clDice【17】开始,介绍拓扑保留的方法。
T p r e c ( S P , V L ) = ∣ S P ∩ V L ∣ ∣ S P ∣ , T s e n s ( S L , V P ) = ∣ S L ∩ V P ∣ ∣ S L ∣ T_{prec}(S_P, V_L) = \frac{|S_P \cap V_L|}{|S_P|}, \quad T_{sens}(S_L, V_P) = \frac{|S_L \cap V_P|}{|S_L|} Tprec(SP,VL)=∣SP∣∣SP∩VL∣,Tsens(SL,VP)=∣SL∣∣SL∩VP∣
clDice ( V P , V L ) = 2 × T p r e c ( S P , V L ) × T s e n s ( S L , V P ) T p r e c ( S P , V L ) + T s e n s ( S L , V P ) \text{clDice}(V_P, V_L) = \frac{2 \times T_{prec}(S_P, V_L) \times T_{sens}(S_L, V_P)}{T_{prec}(S_P, V_L) + T_{sens}(S_L, V_P)} clDice(VP,VL)=Tprec(SP,VL)+Tsens(SL,VP)2×Tprec(SP,VL)×Tsens(SL,VP)
Dice的变化
图2说明了cl-X-Dice的变化。我们的方法将管状结构视为具有可变半径的实体:利用沿中心线的法向圆来表示2D中的绘图线段,使用沿3D中的中心线对齐的圆形截面。这种对齐通过集合基方法促进体积估计。集合 D D D 表示从掩码点( v i v_i vi )到其各自边界的最小距离,定义为 D = { d i ; v i ∣ i ∈ [ 1 , q ] , j ∈ [ 1 , k ] } D = \{d_i; v_i | i \in [1,q], j \in [1,k]\} D={di;vi∣i∈[1,q],j∈[1,k]} ,形成距离图。集合 R R R ,与骨架点 S S S 相关,定义为 R = { r i ; s i ∣ i ∈ [ 1 , n ] , j ∈ [ 1 , m ] } R = \{r_i; s_i | i \in [1,n], j \in [1,m]\} R={ri;si∣i∈[1,n],j∈[1,m]} ,表示每个骨架点( s s s )与其骨架半径( r r r )的距离。 S S S 中的每个骨架点的半径由距离图 D D D 派生,生成集合 R R R 。相反,集合 T = { t i ; b j s ∣ i ∈ [ 1 , n ] , j ∈ [ 1 , m ] } T = \{t_i; b_j^s | i \in [1,n], j \in [1,m]\} T={ti;bjs∣i∈[1,n],j∈[1,m]} 表示骨架半径的集合,表示在 S S S 中的骨架点。 D , R , T D, R, T D,R,T 是 R N \mathbb{R}^N RN 的元素。为了协调骨架线和距离图计算中的差异,超出 R max R_{\max} Rmax 的 D D D 中的值被调整为 R max R_{\max} Rmax 。因此, R R R 的范围为 [ 0 , R max ] [0, R_{\max}] [0,Rmax] 且 D D D 的范围为 [ 1 , R max ] [1, R_{\max}] [1,Rmax] 。对于 p 个掩码点 { v i ∣ i ∈ Z i ∈ [ 1 , p ] } \{v_i | i \in \mathbb{Z}_{i \in [1,p]}\} {vi∣i∈Zi∈[1,p]} ,在2D平面上与中心线或3D截面中的点的距离 d i d_i di ,骨架半径 r r r 范围在 [1, r] 之内。cl-X-Dice度量设计用于解决不同直径血管的分割挑战:
T p r e c ( S P , S L , V L ) = ∣ Q S P ∩ Q V L ∣ ∣ Q S P ∣ T_{prec}(S_P, S_L, V_L) = \frac{|Q_{SP} \cap Q_{VL}|}{|Q_{SP}|} Tprec(SP,SL,VL)=∣QSP∣∣QSP∩QVL∣
T s e n s ( S L , V P ) = ∣ Q L ∩ Q V ∣ ∣ Q L ∣ T_{sens}(S_L, V_P) = \frac{|Q_{L} \cap Q_{V}|}{|Q_{L}|} Tsens(SL,VP)=∣QL∣∣QL∩QV∣
cl-X-Dice ( V P , V L ) = 2 × T p r e c ( S P , S L , V L ) × T s e n s ( S L , V P ) T p r e c ( S P , S L , V L ) + T s e n s ( S L , V P ) \text{cl-X-Dice}(V_P, V_L) = \frac{2 \times T_{prec}(S_P, S_L, V_L) \times T_{sens}(S_L, V_P)}{T_{prec}(S_P, S_L, V_L) + T_{sens}(S_L, V_P)} cl-X-Dice(VP,VL)=Tprec(SP,SL,VL)+Tsens(SL,VP)2×Tprec(SP,SL,VL)×Tsens(SL,VP)
我们定义 U U U 为每个元素为1的 R N \mathbb{R}^N RN 。我们引入变量 Q S P , Q S L , Q V L , Q P Q_{SP}, Q_{SL}, Q_{VL}, Q_{P} QSP,QSL,QVL,QP 来解决几何和血管直径不平衡在分割过程中提出的不同方面。这些变量对于血管结构的详细分析至关重要。表1中提供了cl-X-Dice在血管分割中的综合比较。Q的关键符号定义为:sp = SP, sl = SL, vl = VL, vp = VP, s = SL, v = VL 和 spp = SP \cap VP。此外,归一化比率表示为 R N = R R max R_N = \frac{R}{R_{\max}} RN=RmaxR ,面积比 S N = S P V P S_N = \frac{S_P}{V_P} SN=VPSP ,以及 D N = D R max D_N = \frac{D}{R_{\max}} DN=RmaxD 。图3展示了不同度量对平移、变形和直径不平衡的响应。我们广泛分析了cl-X-Dice度量对几何变换的理论响应。详细证明见补充材料。
图1. 在各种数据集中血管分割面临的挑战。关键特征如下:
- 绿色中心线表示血管连通性;
- 蓝色圆圈表示形态学特征;
- 浅橙色箭头(在浅蓝色框内)指示具有显著直径差异的分支。
图2. 该图显示了分割后的二维视网膜血管,提供了表1中提到的不同变量的可视化示例。
二维示意图描述了从clDice到cbDice的过渡,表现为一个具有变化半径的瓶子。
表1. cl-X-Dice的逐步演变和2D与3D度量的比较。

缩写包括参考(L),预测(P),中心线(cl),Dice(D),骨架(S),掩码(M),逆骨架半径(I),归一化(N),和中心线边界(cb)。在这项研究中,cl-MIN-D等同于cb-D。
3 实验
3.1 数据集
我们在三个血管分割数据集上评估我们提出的方法。DRIVE数据集【19】是二维视网膜血管成像的基准,包含40张彩色眼底照片(584x565像素),分为16张训练图像、4张验证图像和20张测试图像。对于三维CT肺动脉分割,MICCAI 2022 Parse挑战数据集【8】包含100个CT扫描(512x512x228到512x512x376像素),其中80个用于训练,20个用于验证和测试。最后,MICCAI 2023 TopCoW挑战数据集【26】包括90个脑MRA病例(大约481x586x185像素),其中72个用于训练,18个用于验证和测试。

图3. (a) 在仅有平移扰动的情况下,cb-Dice度量对cl-M-Dice变化的敏感性,随着平移距离的增加,与B-Dou相当,而clDice保持不变。 (b) 在均匀缩放(放大或缩小)中,cbDice度量确保了比clDice更一致的评估,能有效适应尺度变化。 © 对于直径不平衡,cbDice一致地评估了各种直径变化,优于clDice。
表2. 经过20个周期的训练后,使用nuU-Net在DRIVE数据集上的结果比较。我们的方法以浅黄色突出显示,最佳分数以粗体显示。

3.2 设置
我们使用PyTorch 2.1进行实验,利用NVIDIA V100以提高计算效率。所有实验都是从头开始在nnU-Net V2框架上训练的【5】。在标准化我们的实验设置时,我们选择不使用深度监督,将批量大小设置为2,并根据每个数据集的默认配置调整nnU-Net的其他参数。此外,对于TopCoW 2023数据集,我们禁用了镜像增强,以防止左右标签的错误翻转。我们严格评估了cbDice损失在TopCoW 2023挑战和其他最近研究的分割模型上的效果。这项评估包括nnU-Net【5】、SwinUNETR【3】和NexToU【16】。比较研究涉及多种损失函数:标准Dice损失、clDice损失【17】、B-Dou损失【21】以及我们提出的cl-M-Dice和cbDice损失。分割性能通过关键指标评估,如重叠(Dice和clDice【17】)、拓扑(Betti数误差和Betti匹配误差【20】)和距离(归一化表面距离(NSD)在1.0mm容差内,参考【12,10】)。我们采用了在【11】中描述的可证明的差分骨架提取算法,并通过cuCIM库实现了加速的欧几里得距离变换。与nnU-Net保持一致,我们使用交叉熵(CE)损失。损失函数定义为: L = 0.5 × C E + α 2 ( α + β ) × D i c e + β 2 ( α + β ) × X L = 0.5 \times CE + \frac{\alpha}{2(\alpha + \beta)} \times Dice + \frac{\beta}{2(\alpha + \beta)} \times X L=0.5×CE+2(α+β)α×Dice+2(α+β)β×X其中,X表示cl-X-Dice或B-Dou【21】。参数α和β是非负数;当两者都设置为0时,恢复为CE损失。
3.3 结果
我们的方法在二维和三维二值分割任务中展示了有效性。表2中详细分析的DRIVE数据集结果表明,cbDice损失显著提高了重叠指标。具体来说,它实现了82.5%的最高Dice得分和82.4%的clDice得分。此外,β = 0.5的cbDice变体达到87.2%的最高NSD。在Parallel中,cl-M-Dice与B-Dou的表现相当。在Parse 2022数据集中,cbDice损失在保持拓扑和几何结构方面表现有效,提高了分割Dice得分,增加了NSD得分,并减少了拓扑错误。

图4. TopCoW 2023数据集结果的比较可视化。黄色箭头标记了分割的假阴性区域,绿色箭头指示假阳性区域,红色箭头标识了分类错误的区域。

表3. Parse 2022 和 TopCoW 2023 数据集结果的综合比较。这里,L 表示大动脉(不连通),S 表示小动脉(连通)。
4 结论
在本研究中,我们介绍了cbDice损失,这是clDice损失框架中的一项创新进展,并通过一系列cl-X-Dice度量进一步阐述了这一进展。这些发展专门针对医学成像中血管分割的复杂性。对不同数据集的广泛评估验证了我们方法在保持拓扑完整性、捕获几何细节和在血管分割任务中保持平衡直径表示方面的有效性。与领先模型和损失函数的比较分析表明,cbDice损失在满足血管分割的复杂需求方面表现出了卓越的能力。
5. 补充材料
clDice变体的理论分析。 本节深入探讨了血管分割中cl-X-Dice度量的理论基础和几何敏感性。我们引入了三个定理来阐明cl-X-Dice度量的行为和计算:
定理 1
对于沿骨架线的垂直平移且无变形情况下,cl-M-Dice系数对半径R内掩码 V V V的平移敏感,而clDice保持不变。
证明。 在二维中,cl-M-Dice定义如下(类似地可扩展到三维):
T p r e c ( S P , S L , V L ) = ∣ S P ∩ D L ∣ ∣ R P ∩ ( U − S L ) ∣ + ∣ S P ∩ R L ∣ T_{prec}(S_P, S_L, V_L) = \frac{|S_P \cap D_L|}{|R_P \cap (U - S_L)| + |S_P \cap R_L|} Tprec(SP,SL,VL)=∣RP∩(U−SL)∣+∣SP∩RL∣∣SP∩DL∣
T s e n s ( S L , S P , V P ) = ∣ S L ∩ D P ∣ ∣ R L ∩ ( U − S P ) ∣ + ∣ S L ∩ R P ∣ T_{sens}(S_L, S_P, V_P) = \frac{|S_L \cap D_P|}{|R_L \cap (U - S_P)| + |S_L \cap R_P|} Tsens(SL,SP,VP)=∣RL∩(U−SP)∣+∣SL∩RP∣∣SL∩DP∣
在保持恒定半径的垂直平移下, ∣ S P ∩ R L ∣ |S_P \cap R_L| ∣SP∩RL∣等于 ∣ S L ∩ R P ∣ |S_L \cap R_P| ∣SL∩RP∣。这将cl-M-Dice的分母减少为 ∣ R P ∣ |R_P| ∣RP∣(对于 R L R_L RL类似),使其敏感性仅依赖于分子。因此,cl-M-Dice对 R R R内 V V V的空间位移作出反应。 相反,clDice评估 S S S和 V V V之间的重叠,不受这些变化的影响。
定理 2
cl-S-Dice与clDice不同,对在无垂直平移下骨架变形的半径变化敏感。在完全重叠的情况下,cl-S-Dice等于值为1的clDice。
证明。 在二维中,cl-S-Dice定义如下(类似地可扩展到三维):
T p r e c ( S P , S L , V L ) = ∣ R P ∩ V L ∣ ∣ R P ∣ , T s e n s ( S L , S P , V P ) = ∣ R L ∩ V P ∣ ∣ R L ∣ T_{prec}(S_P, S_L, V_L) = \frac{|R_P \cap V_L|}{|R_P|}, \quad T_{sens}(S_L, S_P, V_P) = \frac{|R_L \cap V_P|}{|R_L|} Tprec(SP,SL,VL)=∣RP∣∣RP∩VL∣,Tsens(SL,SP,VP)=∣RL∣∣RL∩VP∣
对于clDice ≠ 1(部分重叠),半径的变化( R P R_P RP, R L R_L RL)影响 ∣ R P ∩ V L ∣ |R_P \cap V_L| ∣RP∩VL∣和 ∣ R L ∩ V P ∣ |R_L \cap V_P| ∣RL∩VP∣。具体来说, S = { s i , b j s ∣ i ∈ [ 1 , n ] , j ∈ [ 1 , m ] } S = \{s_i, b_j^s | i \in [1,n], j \in [1,m]\} S={si,bjs∣i∈[1,n],j∈[1,m]}和 R = { r i ; s i , b j s ∣ i ∈ [ 1 , n ] , j ∈ [ 1 , m ] } R = \{r_i; s_i, b_j^s | i \in [1,n], j \in [1,m]\} R={ri;si,bjs∣i∈[1,n],j∈[1,m]},任何 s i s_i si的 r i r_i ri的变化修改cl-S-Dice。 当clDice = 1(完全重叠), ∣ R P ∩ V L ∣ |R_P \cap V_L| ∣RP∩VL∣和 ∣ R L ∩ V P ∣ = ∣ R L ∣ |R_L \cap V_P| = |R_L| ∣RL∩VP∣=∣RL∣,cl-S-Dice与clDice一致,突显了cl-S-Dice在其他情况下对半径变化的敏感性。
定理 3
cl-X-Dice增强了几何敏感性并补偿了直径差异,同时保留了clDice的拓扑完整性。
证明。 cl-X-Dice度量通过引入变量 Q s l Q_{sl} Qsl、 Q s p Q_{sp} Qsp、 Q v l Q_{vl} Qvl和 Q v p Q_{vp} Qvp,提供了对几何变化(包括大小和形状变化)的高级敏感性,同时保持clDice的拓扑保留特性。
T p r e c ( S P , S L , V L ) = ∣ Q s p ∩ Q v l ∣ ∣ Q s p ∩ Q s p v p ∩ ( U − S L ) ∣ + ∣ Q s p ∩ Q s l v l ∣ T_{prec}(S_P, S_L, V_L) = \frac{|Q_{sp} \cap Q_{vl}|}{|Q_{sp} \cap Q_{spvp} \cap (U - S_L)| + |Q_{sp} \cap Q_{slvl}|} Tprec(SP,SL,VL)=∣Qsp∩Qspvp∩(U−SL)∣+∣Qsp∩Qslvl∣∣Qsp∩Qvl∣
T s e n s ( S L , S P , V P ) = ∣ Q s l ∩ Q v p ∣ ∣ Q s l ∩ Q s l v l ∩ ( U − S P ) ∣ + ∣ Q s l ∩ Q s p v p ∣ T_{sens}(S_L, S_P, V_P) = \frac{|Q_{sl} \cap Q_{vp}|}{|Q_{sl} \cap Q_{slvl} \cap (U - S_P)| + |Q_{sl} \cap Q_{spvp}|} Tsens(SL,SP,VP)=∣Qsl∩Qslvl∩(U−SP)∣+∣Qsl∩Qspvp∣∣Qsl∩Qvp∣
方程9和方程10代表了一种平衡的方法,在适应几何变化的同时保持拓扑准确性,从而在拓扑完整性和几何精度之间实现平衡。
相关文章:

MICCAI 2024Centerline Boundary Dice Loss for Vascular Segmentation
MICCAI 2024 Centerline Boundary Dice Loss for Vascular Segmentation MICCAI 2024Centerline Boundary Dice Loss for Vascular Segmentation中心线边界Dice损失用于血管分割**摘要**:1. 引言相关工作: 2. 方法预备知识Dice的变化 3 实验3.1 数据集3.2 设置3.3 结…...

golang验证Etherscan上的智能合约
文章目录 golang验证Etherscan上的智能合约为什么要验证智能合约如何使用golang去验证合约获取EtherscanAPI密钥Verify Source Code接口Check Source Code Verification Status接口演示示例及注意事项网络问题无法调用Etherscan接口(最重要的步骤) golan…...

Visual Studio编译优化选项
目录 /O1 和 /O2 /Ox 内联函数 虚函数优化 代码重排 循环优化 链接时间优化 代码分割 数学优化 其他优化选项 在Visual Studio中,编译优化选项是用于提高程序性能的重要工具。编译器提供了多种优化级别和选项,可以根据不同的需要进行选择。 在…...

sql业务场景分析思路参考
1、时间可以进行排序,也可以用聚合函数对时间求最大值max(时间) 例如下面的例子:取最晚入职的人,那就是将入职时间倒序排序,然后limit 1 表: 场景:查找最晚入职员工的所有信息 se…...

Django权限系统如何使用?
Django的权限系统是一个强大而灵活的特性,允许你控制不同用户对应用程序中资源的访问。以下是使用Django权限系统的几个基本步骤: 1. 定义模型权限 在你的models.py文件中,你可以为每个模型定义自定义权限。这通过在模型的Meta类里设置perm…...
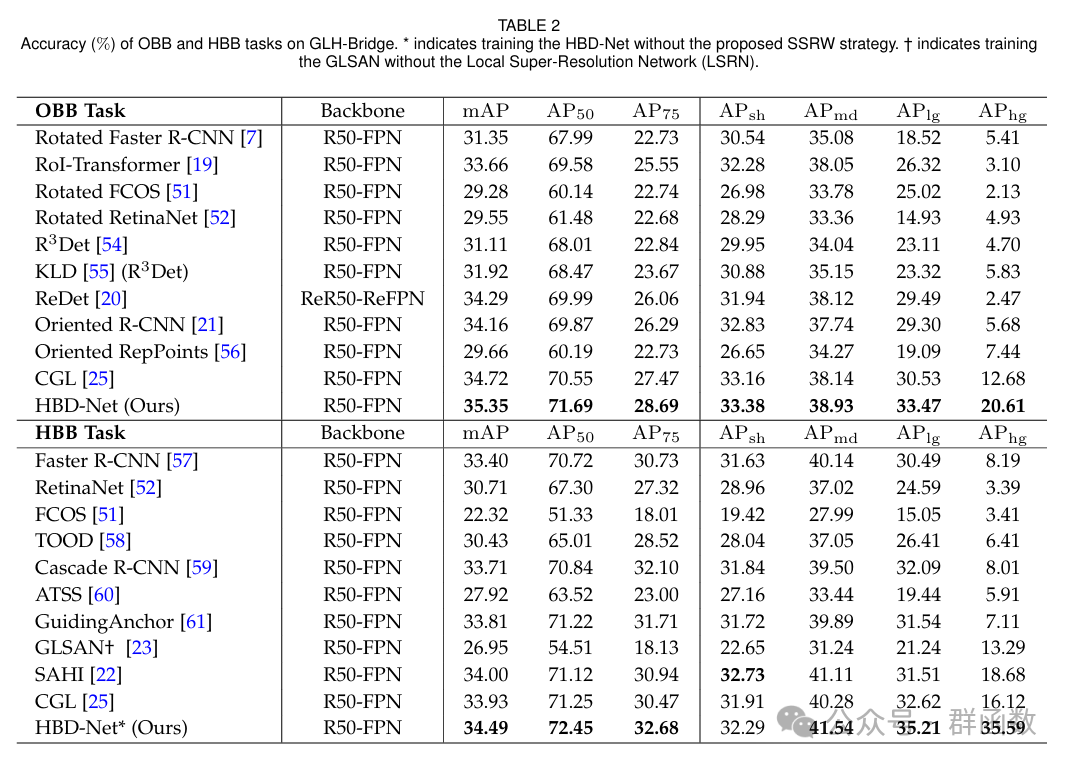
基于整体学习的大幅面超高分遥感影像桥梁目标检测(含数据集下载地址)
文章摘要 在遥感图像(RSIs)中进行桥梁检测在各种应用中起着至关重要的作用,但与其他对象检测相比,桥梁检测面临独特的挑战。在RSIs中,桥梁在空间尺度和纵横比方面表现出相当大的变化。因此,为了确保桥梁的…...

逻辑回归模型(非回归问题,而是解决二分类问题)
目录: 一、Sigmoid激活函数:二、逻辑回归介绍:三、决策边界四、逻辑回归模型训练过程:1.训练目标:2.梯度下降调整参数: 一、Sigmoid激活函数: Sigmoid函数是构建逻辑回归模型的重要激活函数&am…...

QT的OpenGL渲染窗QOpenGLWidget Class
Qt - QOpenGLWidget (class) (runebook.dev) 一、说明 QOpenGLWidget 类是用于渲染 OpenGL 图形的小部件。从Qt 5.4就开始退出,它对于OpenGL有专门的配合设计。 二、QOpenGLWidget类的成员 2.1 Public类函数 QOpenGLWidget(QWidget *parent nullptr,Qt…...

单元测试和集成测试
软件测试中,单元测试和集成测试是比较常见的方法 单元测试:这是一种专注于最小可测试单元(通常是函数或方法)的测试,用于验证单个组件的行为是否符合预期。它通常由开发者自己完成,可以尽早发现问题&#…...

【JAVA入门】Day15 - 接口
【JAVA入门】Day15 - 接口 文章目录 【JAVA入门】Day15 - 接口一、接口是对“行为”的抽象二、接口的定义和使用三、接口中成员的特点四、接口和类之间的关系五、接口中新增的方法5.1 JDK8开始接口中新增的方法5.1.1 接口中的默认方法5.1.2 接口中的静态方法 5.2 JDK9 开始接口…...
)
ES6 之 Set 与 Map 数据结构要点总结(一)
Set 数据结构 Set 对象允许你存储任何类型的唯一值,无论是原始值还是对象引用。 特性: 所有值都是唯一的,没有重复。值的顺序是根据添加的顺序确定的。可以使用迭代器遍历 Set。 常用方法: 1. add(value):添加一个新…...
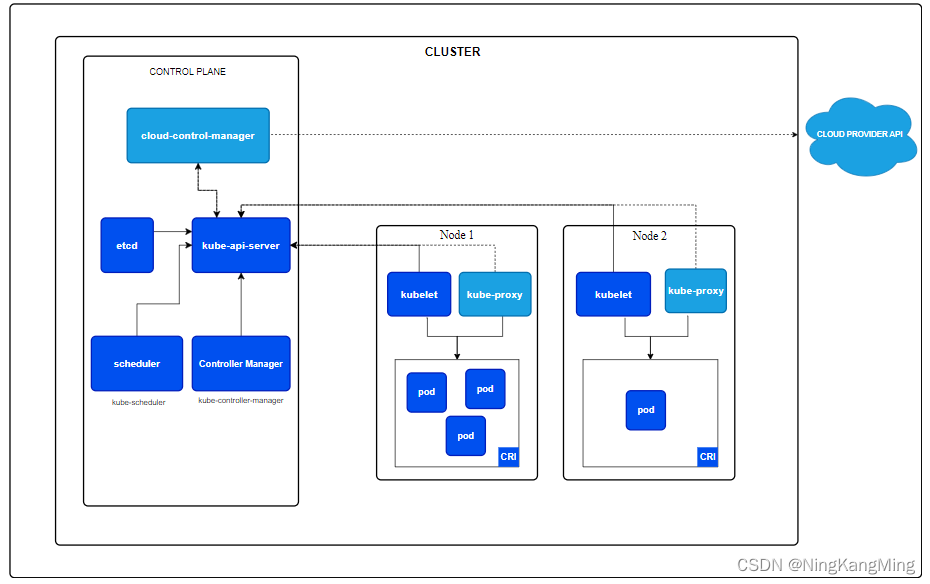
一文学会用RKE部署高可用Kubernetes集群
k8s架构图 RKE简介 RKE全称Rancher Kubernetes Engine,是一个快速的,多功能的 Kubernetes 安装工具。通过RKE,我们可以快速的安装一个高可用K8S集群。RKE 支持多种操作系统,包括 MacOS、Linux 和 Windows。 K8S原生安装需要的先…...

数据加密的常见方法
数据加密是一门历史悠久的技术,它通过加密算法和加密密钥将明文(原始的或未加密的数据)转变为密文,而解密则是通过解密算法和解密密钥将密文恢复为明文。这一技术的核心是密码学,它利用密码技术对信息进行加密,实现信息隐蔽&#…...

天童美语:推荐给孩子的人文历史纪录片
孩子们都有自己的偏好,有的孩子喜欢打游戏,有的孩子喜欢看剧看电影,有的孩子喜欢看书。针对不同的孩子我们要因材施教,所以,广州天童教育给大家推荐一下适合给孩子看的人文历史类的纪录片,让精美的画面&…...

数字人技术如何推动教育事业可持续创新发展?
数字人技术作为一种新兴的教育手段,无论是幼儿园还是大学课堂,数字人都可以融入于各阶段教育中,结合动作捕捉、AI等技术,提高教育资源的利用。 AI智能交互数字人应用: 数字人结合NLP自然语言处理技术以及AI大模型技术…...
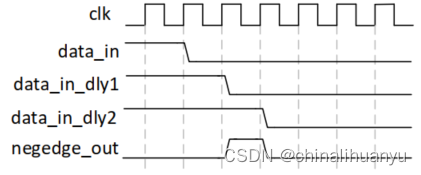
FPGA程序设计
在设计FPGA时,多运用模块化的思想取设计模块,将某一功能设计成module。 设计之前要先画一下模块设计图,列出输入输出接口,再进一步设计内部功能。 状态机要画图,确定每个状态和状态之间怎么切换。状态用localparam定…...

彻底开源,免费商用,上海AI实验室把大模型门槛打下来
终于,业内迎来了首个全链条大模型开源体系。 大模型领域,有人探索前沿技术,有人在加速落地,也有人正在推动整个社区进步。 就在近日,AI 社区迎来首个统一的全链条贯穿的大模型开源体系。 虽然社区有LLaMA等影响力较大…...

MTEB评估基准使用指北
文章目录 介绍评估数据 介绍 文本嵌入通常是在单一任务的少量数据集上进行评估,这些数据集未涵盖其可能应用于其他任务的情况,不清楚在语义文本相似性(semantic textual similarity, STS)等任务上的最先进嵌入是否同样适用于聚类或…...

31. 1049. 最后一块石头的重量 II, 494.目标和,474.一和零
class Solution { public:int lastStoneWeightII(vector<int>& stones) {int sum 0;for(int stone : stones) sum stone;int bagSize sum /2;vector<int> dp(bagSize 1, 0);for(int i 0; i < stones.size(); i){ //遍历物品for(int j bagSize; j >…...

PDF 中图表的解析探究
PDF 中图表的解析探究 0. 引言1. 开源方案探究 0. 引言 一直以来,对文档中的图片和表格处理都非常有挑战性。这篇文章记录一下最近工作上在这块的探究。图表分为图片和表格,这篇文章主要记录了对表格的探究。还有,我个人主要做日本项目&…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...







