逻辑回归模型(非回归问题,而是解决二分类问题)
目录:
- 一、Sigmoid激活函数:
- 二、逻辑回归介绍:
- 三、决策边界
- 四、逻辑回归模型训练过程:
- 1.训练目标:
- 2.梯度下降调整参数:
一、Sigmoid激活函数:
Sigmoid函数是构建逻辑回归模型的重要激活函数,如下图所示。

- 二分类问题目标是将模型的输出结果控制在[0,1]的范围内,当模型输出结果<0.5,默认预测结果为0;当模型输出结果>0.5,默认预测结果为1。
- 二分类问题的解决思路是:通过构建逻辑回归模型f将二分类问题的输入x映射到Sigmoid函数的输入z上计算输出g,再根据g的范围(是否大于0.5)获得逻辑回归模型的结果(即二分类问题的结果)。
- 函数的定义域∈R,值域∈[0,1],当输入z<0时,Sogmoid函数输出结果g<0.5,默认为结果是0,构成二分类问题的第一个类别。当输入z>0时,Sogmoid函数输出结果g>0.5,默认为结果是1,构成二分类问题的第二个类别。
二、逻辑回归介绍:
逻辑回归用来解决二分类问题。分类问题即模型的输出结果只有有限个(回归问题则是无限个),二分类问题即模型的输出结果只有两个。
在回归问题的经典案例“肿瘤预测案例”中,使用肿瘤尺寸size特征预测该肿瘤是否是恶性肿瘤,输出结果只有两种:是(1)或否(0)。

这时使用线性回归模型就很难拟合训练集 (线性回归解决的是回归问题,而肿瘤预测案例是一个分类问题,准确说是二分类问题),因此提出了逻辑回归思想。

逻辑回归模型(解决分类问题):输入特征或特征集X并输出0~1之间的数字,其中拟合曲线通过Sogmoid函数来构造。具体构造流程如下图:


- 第一行解释:逻辑回归模型f的构造同线性回归,通过输入特征集X输出预测结果f,不同点在于f取值范围∈[0,1]。
- 第二三四行解释:之前我们介绍了Sigmoid函数的输出g可以很好的解决二分类问题,因此我们巧妙地使用了Sigmoid函数来构建逻辑回归模型f解决二分类问题,通过将输入特征集X使用线性回归或多项式回归映射到Sigmoid函数的输入z,实现Sigmoid函数的输出,然后根据Sigmoid函数输出结果是否大于0.5来计算逻辑回归模型的输出f(0或1),得到二分类问题的结果。
- 第五行解释:上述思想整合一下即可得出逻辑回归模型f,其中模型的输入是特征集X,输出是分类的预测结果0或1。
- 第六行解释:当逻辑回归模型的输出结果大于等于0.5时,预测值y^为1,用上文的例子来讲就是该肿瘤是恶性肿瘤;当逻辑回归模型的输出结果小于等于0.5时,预测值为0,用上文的例子来讲就是该肿瘤不是恶性肿瘤。
三、决策边界
从上文不难得到,当Sigmoid函数的输入z大于等于0时,即特征集X到z的映射z=wx+b大于等于0时,模型的输出结果是1;当Sigmoid函数的输入z小于0时,即特征集X到z的映射z=wx+b小于0时,模型的输出结果是0。
这是我们可以提出决策边界的概念:使得模型输入X到Sigmoid函数输入z的映射等于0的方程叫做决策边界。
以上述肿瘤预测模型为例,模型输入X到Sigmoid函数输入z的映射为z=wx+b,那么决策边界就是wx+b=0。
下面让我们用图像来展示决策边界的意义:
-
例1:映射为线性函数

上图展示了训练集中特征x1、x2不同取值时标签的真实值,其中圈代表该样本分类结果为0,叉代表该样本分类结果为1。逻辑回归模型如上图,其中模型输入X到Sigmoid函数输入z的映射为z=w1x1+w2x2+b,则决策边界为w1x1+w2x2+b=0。若模型训练结果为w1=1,w2=1,b=-3时,决策边界为x1+x2-3=0,决策边界的函数图像如上图所示,可以看到,如果样本的特征位于决策边界左侧,逻辑回归预测时0,反之为1,这就是决策边界的图像意义。
-
例2:映射为多项式函数

模型输入X到Sigmoid函数输入z的映射为多项式函数,决策边界如图,可以看到,模型训练完成后,参数值确定了,决策边界也立即就确定了,这时样本的特征相对决策边界的位置决定了该样本的预测结果。
四、逻辑回归模型训练过程:
其实和线性回归训练过程一样,只不过是待训练模型(函数)不同而已。
1.训练目标:

2.梯度下降调整参数:

相关文章:

逻辑回归模型(非回归问题,而是解决二分类问题)
目录: 一、Sigmoid激活函数:二、逻辑回归介绍:三、决策边界四、逻辑回归模型训练过程:1.训练目标:2.梯度下降调整参数: 一、Sigmoid激活函数: Sigmoid函数是构建逻辑回归模型的重要激活函数&am…...

QT的OpenGL渲染窗QOpenGLWidget Class
Qt - QOpenGLWidget (class) (runebook.dev) 一、说明 QOpenGLWidget 类是用于渲染 OpenGL 图形的小部件。从Qt 5.4就开始退出,它对于OpenGL有专门的配合设计。 二、QOpenGLWidget类的成员 2.1 Public类函数 QOpenGLWidget(QWidget *parent nullptr,Qt…...

单元测试和集成测试
软件测试中,单元测试和集成测试是比较常见的方法 单元测试:这是一种专注于最小可测试单元(通常是函数或方法)的测试,用于验证单个组件的行为是否符合预期。它通常由开发者自己完成,可以尽早发现问题&#…...

【JAVA入门】Day15 - 接口
【JAVA入门】Day15 - 接口 文章目录 【JAVA入门】Day15 - 接口一、接口是对“行为”的抽象二、接口的定义和使用三、接口中成员的特点四、接口和类之间的关系五、接口中新增的方法5.1 JDK8开始接口中新增的方法5.1.1 接口中的默认方法5.1.2 接口中的静态方法 5.2 JDK9 开始接口…...
)
ES6 之 Set 与 Map 数据结构要点总结(一)
Set 数据结构 Set 对象允许你存储任何类型的唯一值,无论是原始值还是对象引用。 特性: 所有值都是唯一的,没有重复。值的顺序是根据添加的顺序确定的。可以使用迭代器遍历 Set。 常用方法: 1. add(value):添加一个新…...
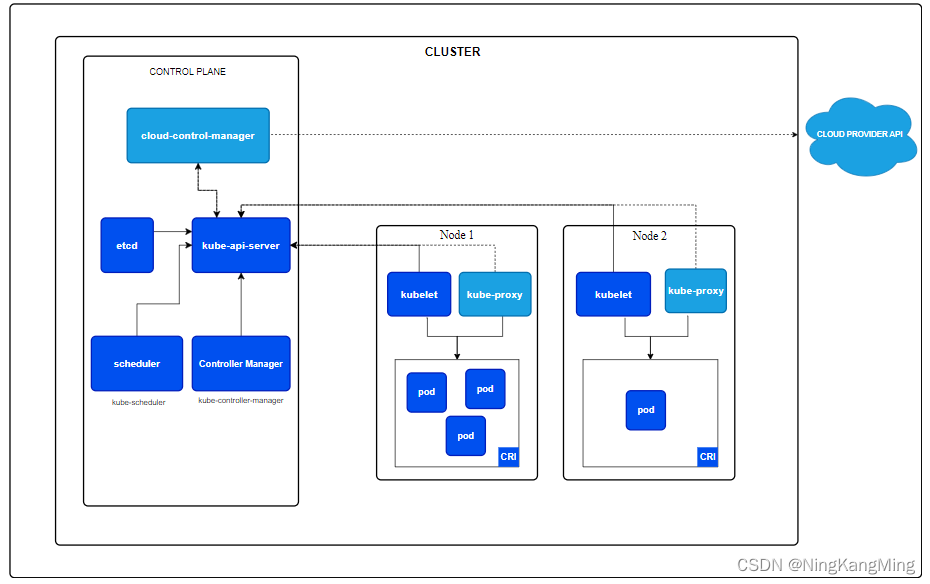
一文学会用RKE部署高可用Kubernetes集群
k8s架构图 RKE简介 RKE全称Rancher Kubernetes Engine,是一个快速的,多功能的 Kubernetes 安装工具。通过RKE,我们可以快速的安装一个高可用K8S集群。RKE 支持多种操作系统,包括 MacOS、Linux 和 Windows。 K8S原生安装需要的先…...

数据加密的常见方法
数据加密是一门历史悠久的技术,它通过加密算法和加密密钥将明文(原始的或未加密的数据)转变为密文,而解密则是通过解密算法和解密密钥将密文恢复为明文。这一技术的核心是密码学,它利用密码技术对信息进行加密,实现信息隐蔽&#…...

天童美语:推荐给孩子的人文历史纪录片
孩子们都有自己的偏好,有的孩子喜欢打游戏,有的孩子喜欢看剧看电影,有的孩子喜欢看书。针对不同的孩子我们要因材施教,所以,广州天童教育给大家推荐一下适合给孩子看的人文历史类的纪录片,让精美的画面&…...

数字人技术如何推动教育事业可持续创新发展?
数字人技术作为一种新兴的教育手段,无论是幼儿园还是大学课堂,数字人都可以融入于各阶段教育中,结合动作捕捉、AI等技术,提高教育资源的利用。 AI智能交互数字人应用: 数字人结合NLP自然语言处理技术以及AI大模型技术…...
FPGA程序设计
在设计FPGA时,多运用模块化的思想取设计模块,将某一功能设计成module。 设计之前要先画一下模块设计图,列出输入输出接口,再进一步设计内部功能。 状态机要画图,确定每个状态和状态之间怎么切换。状态用localparam定…...

彻底开源,免费商用,上海AI实验室把大模型门槛打下来
终于,业内迎来了首个全链条大模型开源体系。 大模型领域,有人探索前沿技术,有人在加速落地,也有人正在推动整个社区进步。 就在近日,AI 社区迎来首个统一的全链条贯穿的大模型开源体系。 虽然社区有LLaMA等影响力较大…...

MTEB评估基准使用指北
文章目录 介绍评估数据 介绍 文本嵌入通常是在单一任务的少量数据集上进行评估,这些数据集未涵盖其可能应用于其他任务的情况,不清楚在语义文本相似性(semantic textual similarity, STS)等任务上的最先进嵌入是否同样适用于聚类或…...

31. 1049. 最后一块石头的重量 II, 494.目标和,474.一和零
class Solution { public:int lastStoneWeightII(vector<int>& stones) {int sum 0;for(int stone : stones) sum stone;int bagSize sum /2;vector<int> dp(bagSize 1, 0);for(int i 0; i < stones.size(); i){ //遍历物品for(int j bagSize; j >…...

PDF 中图表的解析探究
PDF 中图表的解析探究 0. 引言1. 开源方案探究 0. 引言 一直以来,对文档中的图片和表格处理都非常有挑战性。这篇文章记录一下最近工作上在这块的探究。图表分为图片和表格,这篇文章主要记录了对表格的探究。还有,我个人主要做日本项目&…...
)
递推(C语言)
文章目录 1.斐波那契数列2.太波那契数列3.二维递推问题4.实战4.1 力扣509 斐波那契数4.2 力扣70 爬楼梯4.3 力扣119 杨辉三角|| 递推最通俗的理解就是数列,递推和数列的关系就好比 算法 和 数据结构 的关系,数列有点 像数据结构中的线性表(可以是顺序表&…...
安卓微信8.0之后如何利用缓存找回的三天之前不可见的朋友圈图片
安卓微信8.0之后如何利用缓存找回的三天之前不可见的朋友圈图片 复习了下安卓程序的知识,我们会了解到,安卓程序清楚数据的时候有两个选项 一个是清除全部数据一个是清除缓存。 清除全部数据表示清除应用数据缓存。 对于安卓微信8.0之后而言࿰…...
 总结(九))
ES6 Class(类) 总结(九)
ES6 中的 class 是一种面向对象编程的语法糖,提供了一种简洁的方式来定义对象的结构和行为。 JavaScript 语言中,生成实例对象的传统方法是通过构造函数。下面是一个例子。 function Point(x, y) {this.x x;this.y y; } Point.prototype.toString fu…...

使用 Vue.js 和 Element Plus 实现自动完成搜索功能
使用 Vue.js 和 Element Plus 实现自动完成搜索功能 一、前言1.环境准备2.组件配置3.后端数据请求4.样式5.总结 一、前言 在前端开发中,实现自动完成(autocomplete)功能可以极大地提升用户体验,特别是在需要用户输入和选择内容的…...

SpringBoot自定义starter
SpringBoot自定义starter 1、SpringBoot之starter机制 1.1、什么是自定义starter SpringBoot中的starter是一种非常重要的机制(自动化配置),能够抛弃以前繁杂的配置,将其统一集成进starter,应用者只需要在maven中引入starter依赖&#…...

深入探索大语言模型
深入探索大语言模型 引言 大语言模型(LLM)是现代人工智能领域中最为重要的突破之一。这些模型在自然语言处理(NLP)任务中展示了惊人的能力,从文本生成到问答系统,无所不包。本文将从多个角度全面介绍大语…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...

LangFlow技术架构分析
🔧 LangFlow 的可视化技术栈 前端节点编辑器 底层框架:基于 (一个现代化的 React 节点绘图库) 功能: 拖拽式构建 LangGraph 状态机 实时连线定义节点依赖关系 可视化调试循环和分支逻辑 与 LangGraph 的深…...
