自注意力简介
在注意力机制中,每个查询都会关注所有的键值对并生成一个注意力输出。如果查询q,键k和值v都来自于同一组输入,那么这个注意力就被称为是自注意力(self-attention)。自注意力这部分理论,我觉得台大李宏毅老师的课程讲得最好。

自注意力就是输入一堆向量,假设称为a1,a2,a3,a4,那么这四个向量都会参与自注意力机制的运算,得到的结果仍然是四个输出,这四个输出再去做全连接运算。而每一个自注意力机制的输出都用到了a1~a4四个向量来进行运算,也就是说每个输出都是观察了所有的输入之后才得到的。
首先,输入a1需要和a2,a3,a4分别计算相关性,这个相关性可以由缩放点积方式来计算,也就称作缩放点积注意力,也可以由两个两个输入向量相加后再做非线性处理得到,称为加性注意力。

缩放点积的计算方法如下:

输入一个向量v1和一个向量v2,v1去乘上一个可训练矩阵Wq得到q,v2去乘上一个可训练矩阵Wk得到k,再把这个q和k做一个点积运算,得到的就是α,类似于相似度。
回到前面的例子中,a1这里既作为q,又作为k,又作为v。其中,Wq*a1就是q1,Wk*a1就是k1,q1和k1的点积就是α11,相当于a1自己和自己的相似度,同样的,a1和a2,a3,a4分别计算得到α12,α13,α14,然后将α11,α12,α13,α14经过softmax得到最终的四个输出,如下图所示:

然后再用一个可训练矩阵Wv去乘以a1得到v1,用计算得到的相似度α'11去乘以v1,得到一个值temp11;同样的,用可训练矩阵Wv去乘以a2得到v2,用计算得到的相似度α‘12去乘以v2,得到temp12;类似的得到temp13,temp14,然后把temp11+temp12+temp13+temp14得到b1,这个b1就是自注意力机制的第一个输出。

我们刚刚是以a1的视角做的运算,得到b1,同样可以以a2,a3,a4的视角做运算,得到b2,b3,b4。这次就得到了自注意力机制的输出。光看最后这个结构图,有点类似全连接,只是里面的运算过程比全连接要复杂。

下面,我们来看一下如何用代码实现自注意力的计算。
import torch
import torch.nn as nn
import torch.nn.functional as F class SelfAttention(nn.Module):# embed_size代表输入的向量维度,heads代表多头注意力机制中的头数量def __init__(self, embed_size, heads): super(SelfAttention,self).__init__()self.embed_size = embed_sizeself.heads = headsself.head_dim = embed_size // heads # 每个头的维度# 用assert断言机制判断assert (self.head_dim * heads == embed_size), "Embedding size needs to be divisible by heads" # 没有偏置项,其实这个线性层本质上就是为了计算值Wv*a = Vself.values = nn.Linear(self.head_dim, self.head_dim, bias=False)self.keys = nn.Linear(self.head_dim, self.head_dim, bias=False)self.queries = nn.Linear(self.head_dim, self.head_dim, bias=False)# 最后的全连接操作,输出仍是输入的向量维度,也就是说大小是不变的self.fc_out = nn.Linear(heads*self.head_dim, self.embed_size)def forward(self, values, keys, query, mask):# 这个mask也很关键,它用于控制模型在处理序列数据时应该关注哪些部分,以及忽略哪些部分N = query.shape[0] # 获取输入的批量个数print("N:",N)value_len, key_len, query_len = values.shape[1], keys.shape[1], query.shape[1] # 获取输入序列的长度# Split the embedding into self.heads different pieces # 把k,q,v都切分为多个组values = values.reshape(N, value_len, self.heads, self.head_dim)keys = keys.reshape(N, key_len, self.heads, self.head_dim)queries = query.reshape(N, query_len, self.heads, self.head_dim)# 计算k,q,vvalues = self.values(values)keys = self.keys(keys)queries = self.queries(queries)energy = torch.einsum("nqhd,nkhd->nhqk",[queries, keys]) # 格式转化print("queries.shape:", queries.shape)print("keys.shape:", keys.shape)print("energy.shape:", energy.shape)if mask is not None:energy = energy.masked_fill(mask==0, float("-1e20"))attention = torch.softmax(energy/(self.embed_size**(1/2)), dim=3) # softmax内部是缩放点积print("attention.shape:", attention.shape)print("values.shape:", values.shape)out = torch.einsum("nhql,nlhd->nqhd", [attention, values]).reshape(N, query_len, self.heads*self.head_dim)out = self.fc_out(out)return outembed_size = 512
heads = 8
attention = SelfAttention(embed_size, heads)# batch size 1, seq length 60
values = torch.rand(1,60,embed_size)
keys = torch.rand(1,60,embed_size)
queries = torch.rand(1,60,embed_size)
mask = None # 假设没有maskout = attention(values, keys, queries, mask)
print(out.shape)# 输出
N: 1
queries.shape: torch.Size([1, 60, 8, 64])
keys.shape: torch.Size([1, 60, 8, 64])
energy.shape: torch.Size([1, 8, 60, 60])
attention.shape: torch.Size([1, 8, 60, 60])
values.shape: torch.Size([1, 60, 8, 64])
torch.Size([1, 60, 512])通过这个程序,我们可以看到,自注意力机制是不改变输入和输出的形状的,输入的Q,K,V格式是[1,60,512],输出的结果的仍然是[1,60,512]。
下面是几点说明:
1. 这里的embed_size代表的是输入到自注意力层中的每个元素的向量维度。在Transformer模型中,输入数据首先会被转换成一个固定长度的向量,这个向量的长度就称为embed_size。
2. mask表示的是模型在处理序列数据时,应该忽略掉哪部分,我这里设置为None,也就是全部参与计算。
3. einsum,称为爱因斯坦求和,起源是爱因斯坦在研究广义相对论时,需要处理大量求和运算,为了简化这种繁复的运算,提出了求和约定,推动了张量分析的发展。einsum 可以计算向量、矩阵、张量运算,如果利用得当,sinsum可完全代替其他的矩阵计算方法。
例如,C = einsum('ij,jk->ik', A, B),就相当于两个矩阵求内积:cik = Σj AijBjk。
通过输出可以看到,在计算前queries的形状是[1,60,8,64],keys的形状是[1,60,8,64],在表达式"nqhd,nkhd->nhqk"中,n=1,q=60,h=8,d=64,k=60,两个矩阵进行内积,因此得到的结果是nhqk,也就是[1,8,60,60]。
相关文章:

自注意力简介
在注意力机制中,每个查询都会关注所有的键值对并生成一个注意力输出。如果查询q,键k和值v都来自于同一组输入,那么这个注意力就被称为是自注意力(self-attention)。自注意力这部分理论,我觉得台大李宏毅老师…...

【GameFramework框架】7-2、GameFramework框架是否“过度设计”?
推荐阅读 CSDN主页GitHub开源地址Unity3D插件分享简书地址QQ群:398291828大家好,我是佛系工程师☆恬静的小魔龙☆,不定时更新Unity开发技巧,觉得有用记得一键三连哦。 一、前言 【GameFramework框架】系列教程目录: https://blog.csdn.net/q764424567/article/details/1…...
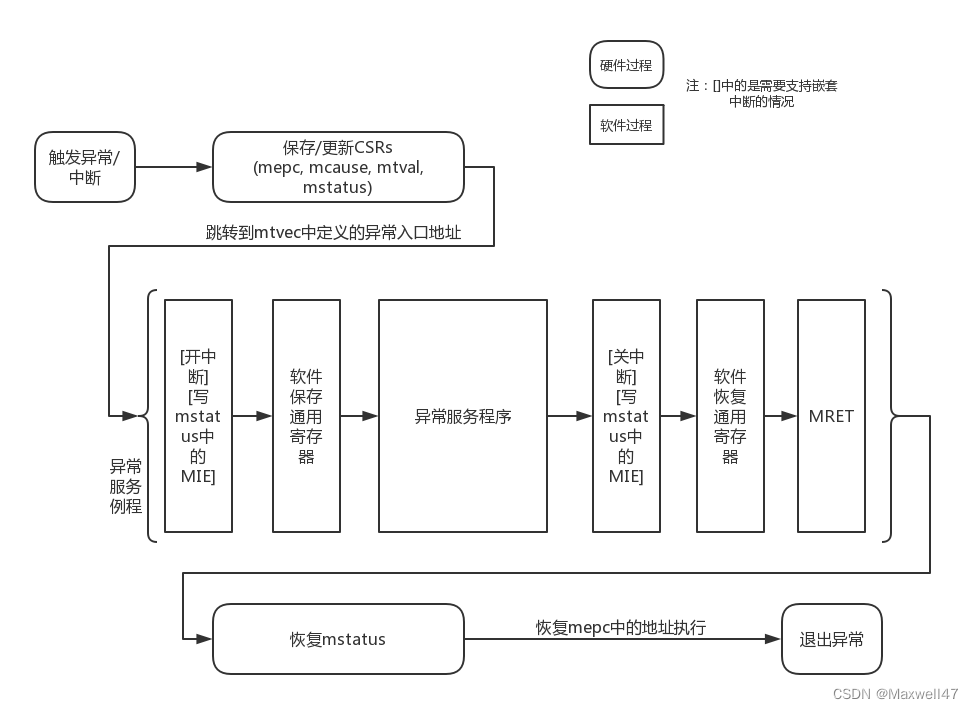
RISC-V异常处理流程概述(2):异常处理机制
RISC-V异常处理流程概述(2):异常处理机制 一、异常处理流程和异常委托1.1 异常处理流程1.2 异常委托二、RISC-V异常处理中软件相关内容2.1 异常处理准备工作2.2 异常处理函数2.3 Opensbi系统调用的注册一、异常处理流程和异常委托 1.1 异常处理流程 发生异常时,首先需要执…...

Unity3D中如何降低游戏的Drawcall详解
在Unity3D游戏开发中,Drawcall是一个至关重要的性能指标,它指的是CPU通知GPU绘制一个物体的命令次数。过多的Drawcall会导致游戏性能下降,因此优化Drawcall的数量是提高游戏性能的关键。本文将详细介绍Unity3D中降低Drawcall的几种主要方法&a…...

小程序-设置环境变量
在实际开发中,不同的开发环境,调用的接口地址是不一样的 例如:开发环境需要调用开发版的接口地址,生产环境需要正式版的接口地址 这时候,我们就可以使用小程序提供了 wx.getAccountInfoSync() 接口,用来获取…...

【RabbitMQ】一文详解消息可靠性
目录: 1.前言 2.生产者 3.数据持久化 4.消费者 5.死信队列 1.前言 RabbitMQ 是一款高性能、高可靠性的消息中间件,广泛应用于分布式系统中。它允许系统中的各个模块进行异步通信,提供了高度的灵活性和可伸缩性。然而,这种通…...

RuntimeError: Unexpected error from cudaGetDeviceCount
RuntimeError: Unexpected error from cudaGetDeviceCount 0. 引言1. 临时解决方法 0. 引言 使用 vllm-0.4.2 部署时,多卡正常运行。升级到 vllm-0.5.1 时,报错如下: (VllmWorkerProcess pid30692) WARNING 07-12 08:16:22 utils.py:562] U…...
基础认知)
uboot学习:(一)基础认知
目录 uboot是一个裸机程序(bootloader) 作用 要运行linux系统时,如何从外置的flash拷贝到DDR中,才能启动 uboot使用步骤 步骤1中的命令例子 注意 uboot源码获取方法 uboot是一个裸机程序(bootloader)…...
- 总体方差)
每天一个数据分析题(四百二十六)- 总体方差
为了比较两个总体方差,我们通常检验两个总体的() A. 方差差 B. 方差比 C. 方差乘积 D. 方差和 数据分析认证考试介绍:点击进入 题目来源于CDA模拟题库 点击此处获取答案 数据分析专项练习题库 内容涵盖Python,SQL,统计学&a…...

【C++】设计一套基于C++与C#的视频播放软件
在开发一款集视频播放与丰富交互功能于一体的软件时,结合C的高性能与C#在界面开发上的便捷性,是一个高效且实用的选择。以下,我们将概述这样一个系统的架构设计、关键技术点以及各功能模块的详细实现思路。 一、系统架构设计 1. 架构概览 …...

数学建模中的辅助变量、中间变量、指示变量
在数学建模中,除了决策变量外,还有一些其他类型的变量,如中间变量、辅助变量和指示变量。每种变量在模型中都有特定的用途和意义。以下是对这些变量的详细解释: 1. 决策变量(Decision Variables) 定义&am…...
和tell())
python的seek()和tell()
seek() seek() 是用来在文件中移动指针位置的方法。它的作用是将文件内部的当前位置设置为指定的位置。 seek(offset, whence) 参数说明 offset: 这是一个整数值,表示相对于起始位置的偏移量。如果是正数,表示向文件末尾方向移动;如果是负…...

Go泛型详解
引子 如果我们要写一个函数分别比较2个整数和浮点数的大小,我们就要写2个函数。如下: func Min(x, y float64) float64 {if x < y {return x}return y }func MinInt(x, y int) int {if x < y {return x}return y }2个函数,除了数据类…...

【每日一练】python之sum()求和函数实例讲解
在Python中, sum()是一个内置函数,用于计算可迭代对象(如列表、元组等)中所有元素的总和。如下实例: """ 收入支出统计小程序 知识点:用户输入获取列表元素添加sum()函数,统计作用 "&…...

打造智慧校园德育管理,提升学生操行基础分
智慧校园的德育管理系统内嵌的操行基础分功能,是对学生日常行为规范和道德素养进行量化评估的一个创新实践。该功能通过将抽象的道德品质转化为具体可量化的指标,如遵守纪律、尊师重道、团结协作、爱护环境及参与集体活动的积极性等,为每个学…...

自定义函数---随机数系列函数
大家有没有发现平常在写随机数的时候,需要引入很多的头文件,然后还需要用一些复杂的函数,大家可能不太习惯,于是我就制作了一个头文件 // random_number.h #ifndef RANDOM_NUMBER_H // 预处理指令,防止头文件被重复包含…...
一文了解5G新通话技术演进与业务模型
5G新通话简介 5G新通话,也被称为VoNR,是基于R16及后续协议产生的一种增强型语音通话业务。 它在IMS网络里新增数据通道(Data Channel),承载通话时的文本、图片、涂鸦、菜单等信息。它能在传统话音业务基础上提供更多服…...

视频使用操作说明书-T80002系列视频编码器如何对接海康NVR硬盘录像机,包括T80002系列高清HDMI编码器、4K超高清HDMI编码器
视频使用操作说明书-T80002系列视频编码器如何对接海康NVR硬盘录像机,包括T80002系列高清HDMI编码器、4K超高清HDMI编码器。 视频使用操作说明书-T80002系列视频编码器如何对接海康NVR硬盘录像机,包括T80002系列高清HDMI编码器、4K超高清HDMI编码器 同三…...

el-input-number计数器change事件校验数据,改变绑定数据值后change方法失效问题的原因及解决方法
在change事件中如果对el-input-number绑定的数据进行更改,会出现change事件失效的问题 试过:this.$set()及赋值等方法,都无法解决 解决方法:用$nextTick函数对绑定值进行更改( this.$nextTick(() > { this.绑定…...

将vue项目整合到springboot项目中并在阿里云上运行
第一步,使用springboot中的thymeleaf模板引擎 导入依赖 <!-- thymeleaf 模板 --><dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-thymeleaf</artifactId></dependency> 在r…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...

CVPR2025重磅突破:AnomalyAny框架实现单样本生成逼真异常数据,破解视觉检测瓶颈!
本文介绍了一种名为AnomalyAny的创新框架,该方法利用Stable Diffusion的强大生成能力,仅需单个正常样本和文本描述,即可生成逼真且多样化的异常样本,有效解决了视觉异常检测中异常样本稀缺的难题,为工业质检、医疗影像…...

提升移动端网页调试效率:WebDebugX 与常见工具组合实践
在日常移动端开发中,网页调试始终是一个高频但又极具挑战的环节。尤其在面对 iOS 与 Android 的混合技术栈、各种设备差异化行为时,开发者迫切需要一套高效、可靠且跨平台的调试方案。过去,我们或多或少使用过 Chrome DevTools、Remote Debug…...
