【数组、特殊矩阵的压缩存储】
目录
- 一、数组
- 1.1、一维数组
- 1.1.1 、一维数组的定义方式
- 1.1.2、一维数组的数组名
- 1.2、二维数组
- 1.2.1、二维数组的定义方式
- 1.2.2、二维数组的数组名
- 二、对称矩阵的压缩存储
- 三、三角矩阵的压缩存储
- 四、三对角矩阵的压缩存储
- 五、稀疏矩阵的压缩存储
一、数组
概述:数组是一个集合,用于存放相同数据类型的元素
1. 特点一: 数组中的每个数据元素具有相同的数据类型;
2. 特点二: 数据占用一段连续的内存空间
1.1、一维数组
1.1.1 、一维数组的定义方式
- 只能用数字,字母和下划线命名,且不能用数字作为开头,注意数组名不要与其他变量名重复;
- 数组的下标从0开始。
一维数组的三种定义方式:
第一种:
//数据类型 数组名[数组长度];
int main(){int arr[10];//定义一个长度为10的数组,数组元素为int型//使用数组下标对数组元素进行访问arr[0] = 10;//数组第一个元素的下标为0arr[2] = 20;arr[9] = 20;//数组最后一个元素的下标为9,对于长度为i的数组,最后一位元素的下标即为i-1
}
注意:定义数组时,若未给定数组元素的初始值,则必须指定数组的长度,否则提示错误,因为编译时需要分配空间,数组长度未知的话,无法进行分配。
第二种:
//数据类型 数组名[数组长度] = {值1, 值2,...};
int main(){int arr[10] = {1, 2, 3, 4};//未设定初始值的后6位元素默认为0
}
注意: 数组初始化时,若大括号{}内的元素个数小雨定义的数组长度,则剩余的数组元素默认为0。
第三种:
//数据类型 数组名[] = {值1, 值2, ...};
int main(){int arr[] = {1,2,3,4,5,6,7,8,9,10};//数组长度为10
}
注意: 定义数组元素时,数组可以不用指定数组长度,数组长度由所定义元素的数量决定。
1.1.2、一维数组的数组名
作用一: 统计数组所占用的内存空间、数组中单个数据元素所占用的内存空间、数组的长度,如下:
#include<iostream>
using namespace std;int main(){int arr[10];cout<<"数组arr用内存空间为"<<sizeof(arr)<<endl;//40cout<<"数组arr中单个元素占用内存空间为:"<<sizeof(arr[0])<<endl;//4cout<<"数组长度为:"<<sizeof(arr)/sizeof(arr[0])<<endl;//10return 0;
}
作用二: 获取数组在内存中的地址,如下:
int main(){int arr[10];cout<<arr<<endl;//获取数组的首地址cout<<&arr[0]<<endl;//获取数组的首地址cout<<&arr<<endl;//获取整个数组的地址return 0;
}
注意: arr/&arr[0]和&arr虽然数值相同,但是含义不同!&数组名表示指针,对程序做出如下变化:
#include<iostream>using namespace std;int main() {int arr[10];cout << "数组长度为:" << sizeof(arr) << endl;cout << "" << sizeof(arr[0])<< endl;cout << "首地址为:"<<arr<<endl;cout << "地址为:" << arr+1<< endl;//与之前相差4cout << "首地址为:" << &arr[0] << endl;cout << "数组地址为:" << &arr << endl;cout << "地址为:" << &arr +1<< endl;//与之前相差了40return 0;
}
运行结果为:

注意:
- 数组名是常量,不能进行赋值,否则会报错;
1.2、二维数组
1.2.1、二维数组的定义方式
二维数组有四种定义方式;
数据类型 数组名[行数][列数];数据类型 数组名[行数][列数] = {数据1, 数据2, 数据3};数据类型 数组名[行数][列数] = {{数据1, 数据2}, {数据3, 数据4},{数据5, 数据6}};数据类型 数组名[][列数] = {数据1, 数据2, 数据3, 数据4};
第3种定义方式最直观,可以提高代码的可读性;
第2种和第4种要根据二维数组的列数推断数组元素**(可以省略行数,不能省略列数)**;
定义二维数组时,若已经初始化数据,可以省略行数。
示例如下:
#include<iostream>using namespace std;int main() {int arr[][2] = { {1,2},{4,5} };for (int i = 0; i < sizeof(arr) / sizeof(arr[0]); i++) {for (int j = 0; j < sizeof(arr[i]) / sizeof(arr[i][0]);j++) {cout << arr[i][j] << "";}cout << endl;}return 0;
}
运行结果为:

注意cout时的格式!
1.2.2、二维数组的数组名
二维数组名称的作用:
1. 计算二维数组所占内存空间;
cout << "二维数组所占空间为:" <<sizeof(arr) <<endl;cout << "二维数组中第1行所占空间为:" << sizeof(arr[0]) << endl;cout << "二维数组中某个元素所占空间为:" << sizeof(arr[0][1]) << endl;
运行结果为:

2. 计算二维数组的行数和列数
求行数:sizeof(arr)/sizeof(arr[0]);//即数组元素总数/每一行的元素数
求列数:sizeof(arr[0])/sizeof(arr[0][0])
3. 获取二维数组中的相关地址
二维数组首地址:arr[0]或者&arr[0][0]
二维数组第一个元素的地址:arr[0]或&arr[0][0]
二维数组第一行的地址:arr或arr[0]或arr+0或*(arr+0)
二维数组第i行的地址:arr[i]或&arr[0]+i或*(arr+i)
二维数组第i行首元素的地址:arr[i]或arr+i或&arr[0]+i或*(arr+i)
二维数组第i行第j列元素的地址:&arr[i][j]或*(arr+i)+j
4. 通过指针解引用访问或操作某元素:*(*(arr+i)+j)
二、对称矩阵的压缩存储
对称矩阵的矩阵压缩:
若n阶方阵中任意一个元素 都有
都有 ,则称该矩阵为对称矩阵,对于对称矩阵,只须存储对角线+下三角区。若按照优先原则将各元素存入一维数组中,即
,则称该矩阵为对称矩阵,对于对称矩阵,只须存储对角线+下三角区。若按照优先原则将各元素存入一维数组中,即 存入数组
存入数组 中,那么数组
中,那么数组 共有
共有 个元素。对于k,有:
个元素。对于k,有:


三、三角矩阵的压缩存储
- 下三角矩阵:除了主对角线和下三角区,其余的元素都相同;
- 上三角矩阵:除了主对角线和上三角区,其余的元素都相同。
- 压缩存储策略:按行优先原则将主对角线+下三角区存入一维数组中,并在最后一个位置存储常量,即
 存入数组
存入数组 中,那么数组
中,那么数组 共有
共有 个元素。对于k,有:
个元素。对于k,有:


四、三对角矩阵的压缩存储
三对角矩阵:又称为带状矩阵:当 时,有
时,有 。对于三角矩阵,按行优先原则,只存储带状部分,即
。对于三角矩阵,按行优先原则,只存储带状部分,即 存入数组
存入数组 中,那么k=2ij - 3。若一直数组下标k,则
中,那么k=2ij - 3。若一直数组下标k,则

五、稀疏矩阵的压缩存储
稀疏矩阵的非零元素远远少于矩阵元素的个数,压缩存储策略:
- 三元数组<行, 列,值>
| i(行) | j(列) | v(值) |
|---|---|---|
| 1 | 3 | 4 |
| 1 | 6 | 5 |
| 2 | 2 | 3 |
| 2 | 4 | 9 |
| 3 | 5 | 6 |
| 4 | 2 | 2 |
注意:此处的行列下标从1开始。
- 十字链表
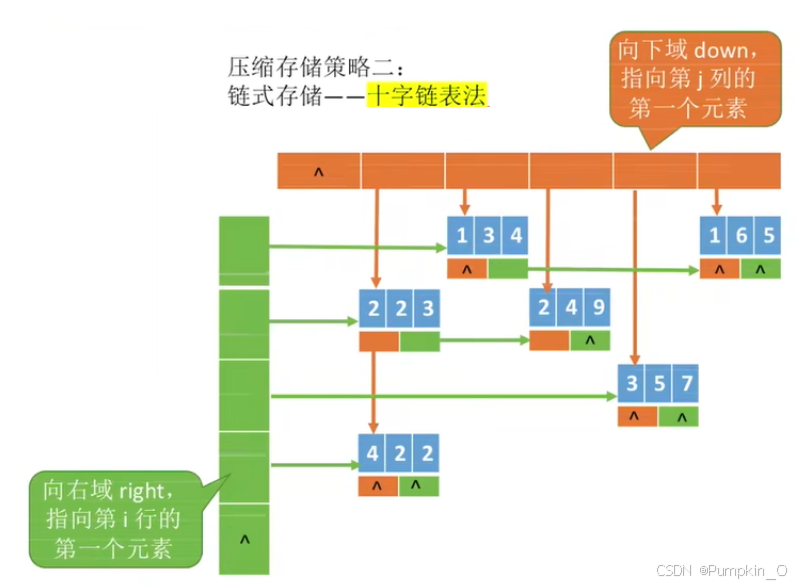
相关文章:

【数组、特殊矩阵的压缩存储】
目录 一、数组1.1、一维数组1.1.1 、一维数组的定义方式1.1.2、一维数组的数组名 1.2、二维数组1.2.1、二维数组的定义方式1.2.2、二维数组的数组名 二、对称矩阵的压缩存储三、三角矩阵的压缩存储四、三对角矩阵的压缩存储五、稀疏矩阵的压缩存储 一、数组 概述:数…...

Flat Ads:金融APP海外广告投放素材的优化指南
在当今全球化的数字营销环境中,金融APP的海外营销推广已成为众多金融机构与开发者最为关注的环节之一。面对不同地域、文化及用户习惯的挑战,如何优化广告素材,以吸引目标受众的注意并促成有效转化,成为了广告主们亟待解决的问题。 作为领先的全球化营销推广平台,Flat Ads凭借…...
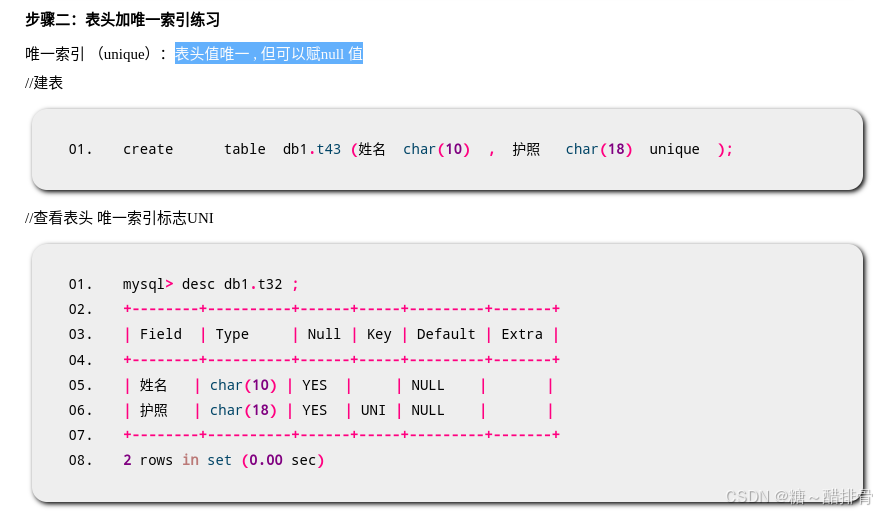
DBA 数据库管理 表管理 数据批量处理。表头约束
表管理 建库 库名命名规则:仅可以使用数字、字母、下划线、不能纯数字 不可使用MySQL命令或特殊字符 库名区分字母大小写 加if not exists 命令避免重名报错 create database if not exists gamedb; 建表 drop database if exists gamedb ; 删表…...
C# 上位机开发之旅-委托事件的那些事[2]
上位机项目开发过程,应该不少遇见界面同步实时刷新的情况,设备的运行情况以及设备数据的实时更新,应用场景非常之多。 那么这个时候,我们就可以用到C#语言中的一些关键功能来实现,比如事件,委托,…...
浏览器出现 502 Bad Gateway的原理分析以及解决方法
目录 前言1. 问题所示2. 原理分析3. 解决方法 前言 此类问题主要作为疑难杂症 1. 问题所示 2. 原理分析 502 Bad Gateway 错误表示服务器作为网关或代理时,从上游服务器收到了无效的响应 通常出现在充当代理或网关的网络服务器上,例如 Nginx、Apache…...
Java的高级特性
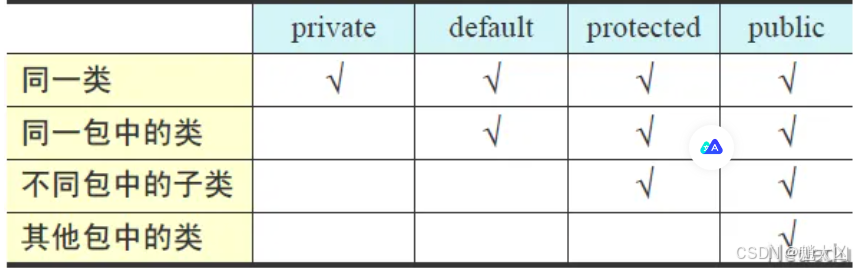
类的继承 继承是从已有的类中派生出新的类,新的类能拥有已有类的属性和行为,并且可以拓展新的属性和行为 public class 子类 extends 父类{子类类体 } 优点 代码的复用 提高编码效率 易于维护 使类与类产生关联,是多态的前提 缺点 类缺乏独…...

pip install selenium异常
error: externally-managed-environment This environment is externally managed ╰─> To install Python packages system-wide, try brew install xyz, where xyz is the package you are trying to install. If you wish to install a Python library that isnt in Ho…...

应急响应总结
应急响应 日志 windows IIS 6.0 及更早版本: C:\WINDOWS\system32\LogFiles\W3SVC[SiteID]\ IIS 7.0 及更高版本: C:\inetpub\logs\LogFiles\W3SVC[SiteID]\ Apache HTTP Server C:\Program Files (x86)\Apache Group\Apache2\logs\ 或者 C:\Prog…...
)
一些资源(●ˇ∀ˇ●)
GPT Kimi.ai - 帮你看更大的世界 (moonshot.cn) 文心一言 (baidu.com) 搜索AI伙伴 (baidu.com) 讯飞星火大模型-AI大语言模型-星火大模型-科大讯飞 (xfyun.cn) 秘塔AI搜索 (metaso.cn) GitHub打不开 下载Watt Toolkit...
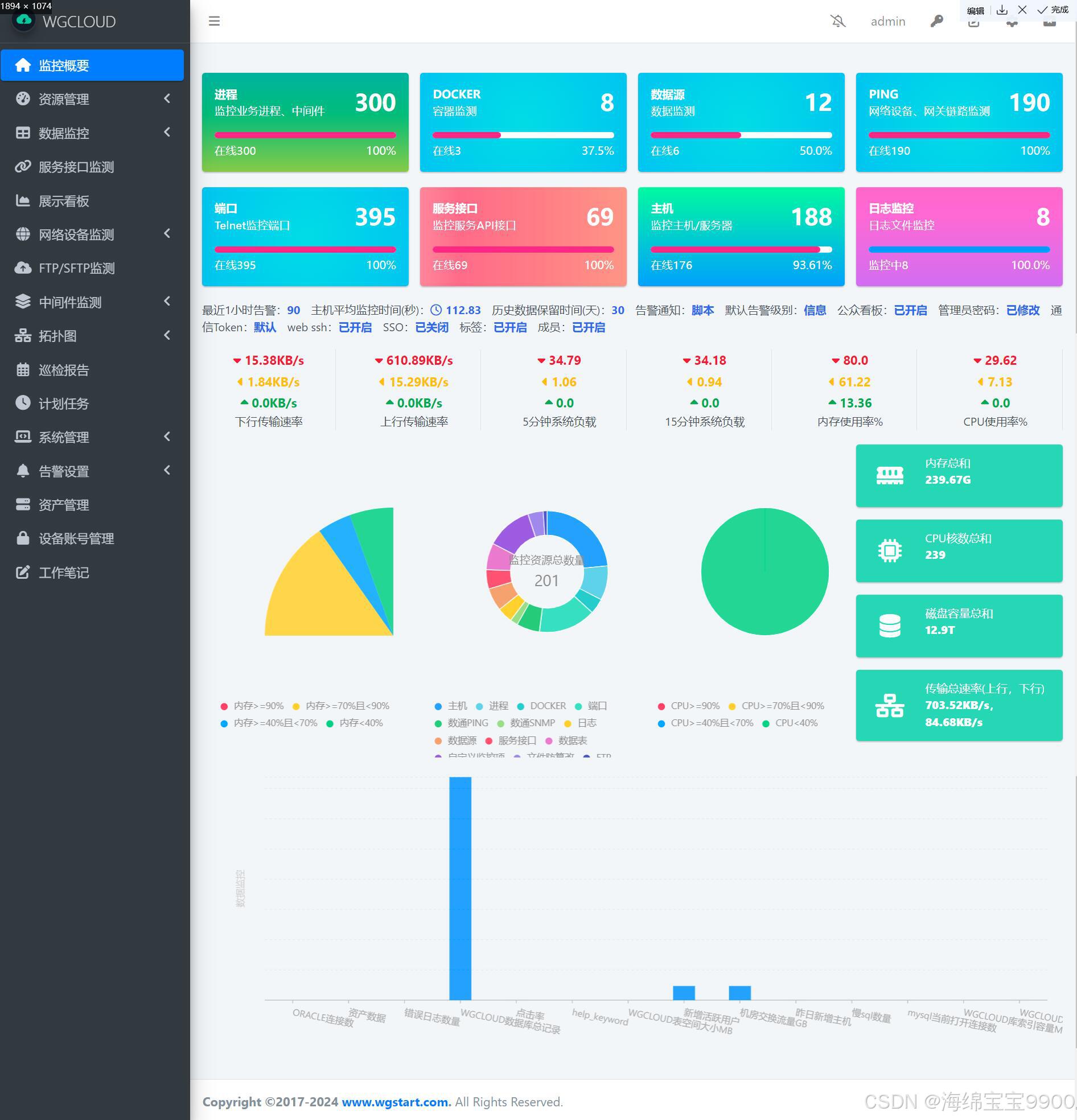
WGCLOUD的ping设备监测可以导入excel数据吗
可以的 WGCLOUD的v3.5.3版本,已经支持导入excel数据,如下说明 数通设备PING监测使用说明 - WGCLOUD...

vue 画二维码及长按保存
需求 想要做如下图的二维码带文字,且能够长按保存 前期准备 一个canvas安装qrcode(命令:npm i qrcode) 画二维码及文字 初始化画布 <template><div><canvas ref"canvas" width"300" he…...
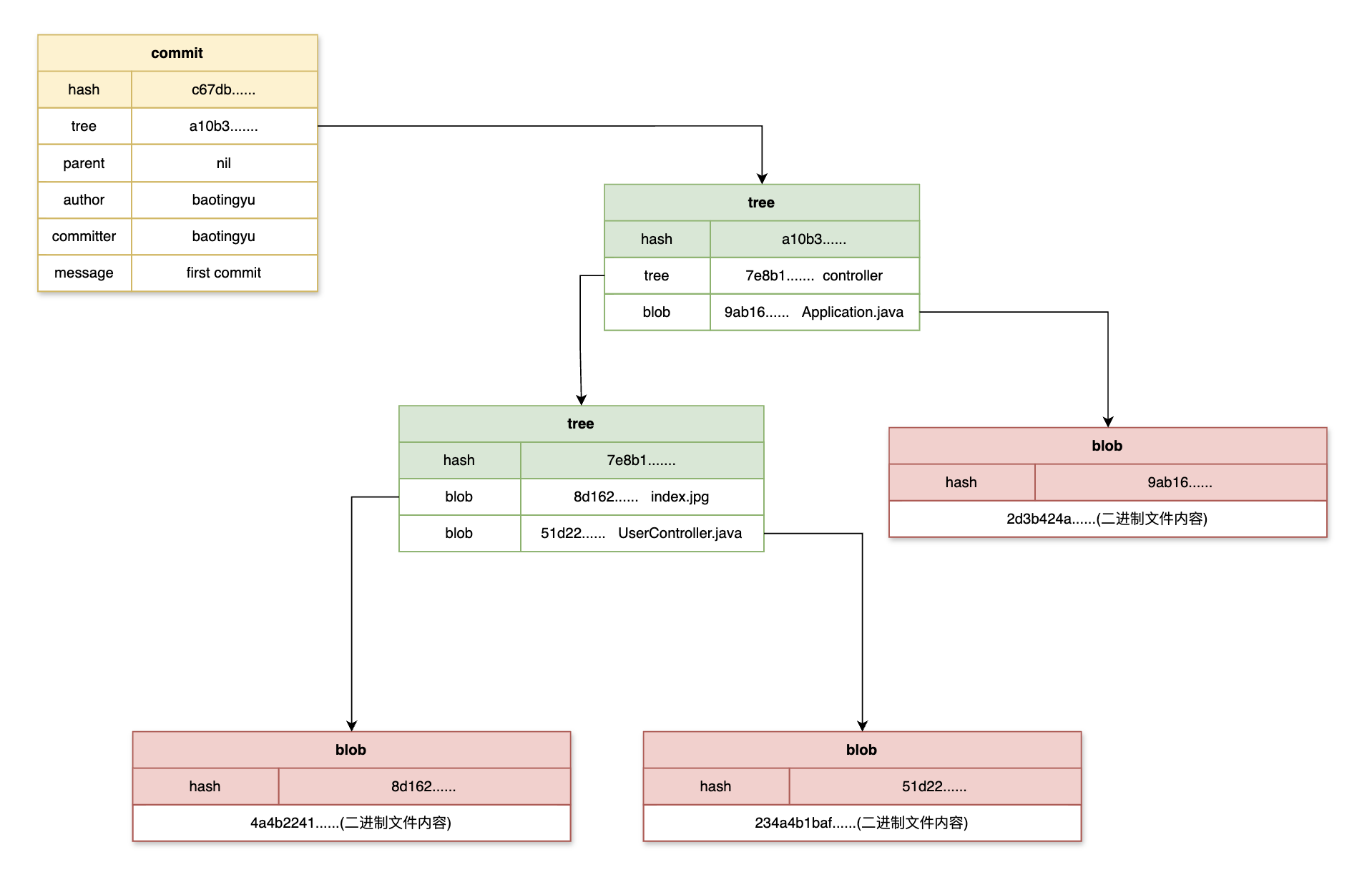
IDEA中Git常用操作及Git存储原理
Git简介与使用 Intro Git is a free and open source distributed version control system designed to handle everything from small to very large projects with speed and efficiency. Git是一款分布式版本控制系统(VSC),是团队合作开发…...
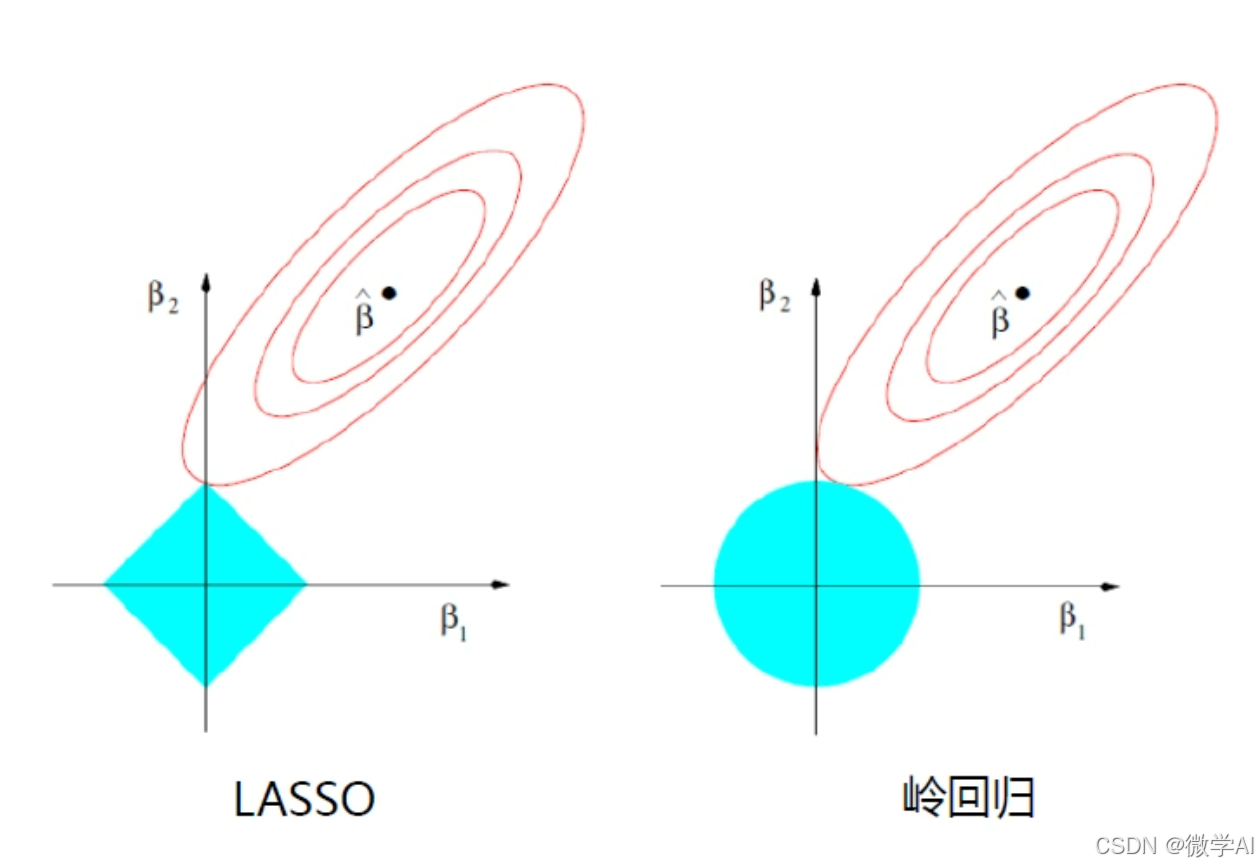
人工智能算法工程师(中级)课程4-sklearn机器学习之回归问题与代码详解
大家好,我是微学AI,今天给大家介绍一下人工智能算法工程师(中级)课程4-sklearn机器学习之回归问题与代码详解。回归分析是统计学和机器学习中的一种重要方法,用于研究因变量和自变量之间的关系。在机器学习中,回归算法被广泛应用于…...

智能制造热点词汇科普篇——工业微服务
随着互联网技术的不断发展,近十年来,微服务也逐渐走进人们的视线中来。何为微服务?让我们先来看看百度百科上的定义:微服务(或称微服务架构)是一种云原生架构方法,在单个应用中包含众多松散耦合…...
FastGPT+OneAI接入网络模型
文章目录 FastGPT连接OneAI接入网络模型1.准备工作2.开始部署2.1下载 docker-compose.yml2.2修改docker-compose.yml里的参数 3.打开FastGPT添加模型3.1打开OneAPI3.2接入网络模型3.3重启服务 FastGPT连接OneAI接入网络模型 1.准备工作 本文档参考FastGPT的官方文档 主机ip接…...
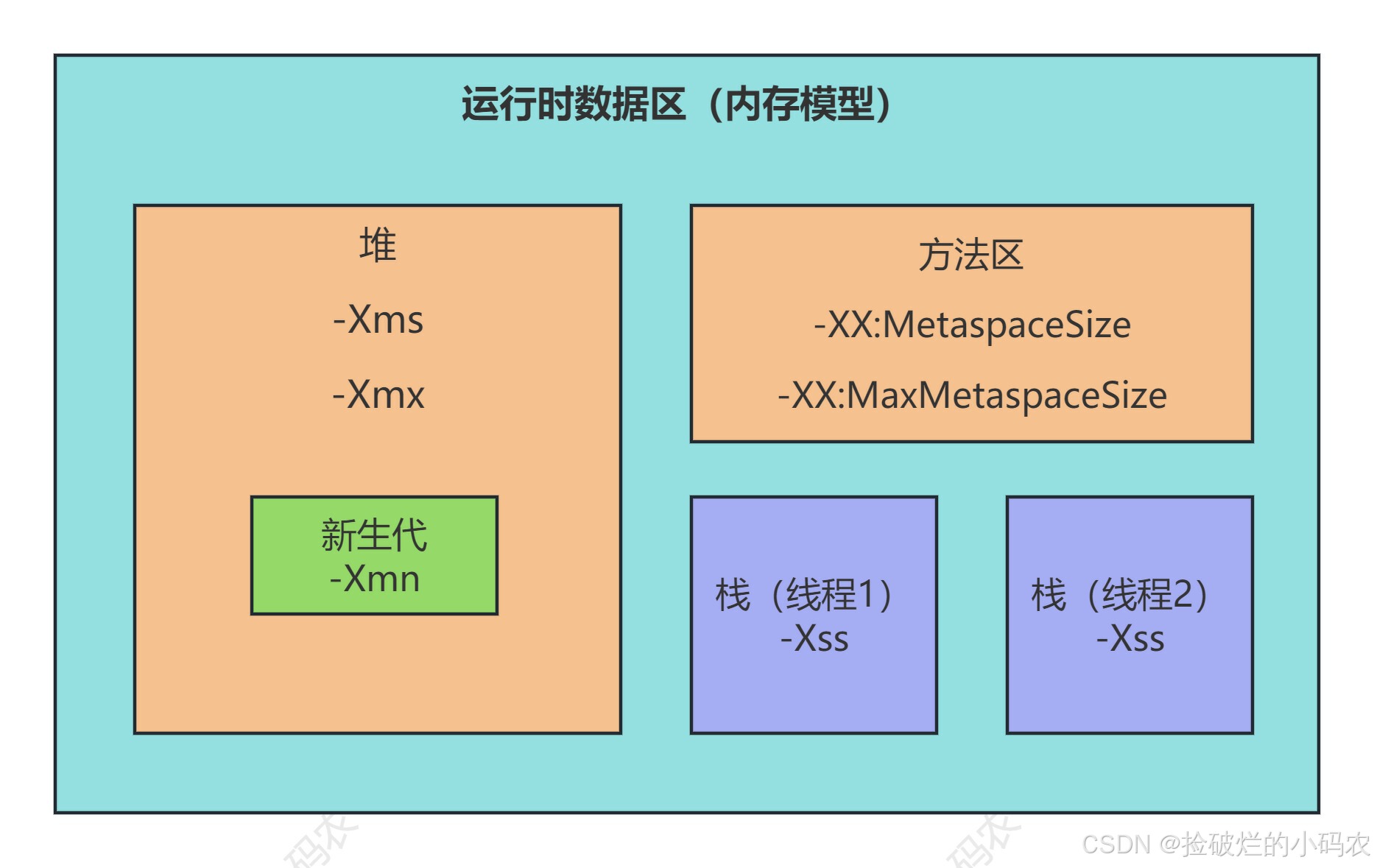
Java核心篇之JVM探秘:内存模型与管理初探
系列文章目录 第一章 Java核心篇之JVM探秘:内存模型与管理初探 第二章 Java核心篇之JVM探秘:对象创建与内存分配机制 第三章 Java核心篇之JVM探秘:垃圾回收算法与垃圾收集器 第四章 Java核心篇之JVM调优实战:Arthas工具使用及…...

未来互联网的新篇章:深度解析Facebook的技术与战略
随着科技的飞速发展和社会的不断变迁,互联网作为全球信息交流的重要平台,正经历着前所未有的变革和演进。作为全球最大的社交媒体平台之一,Facebook不仅是人们沟通、分享和互动的重要场所,更是科技创新和数字化进程的推动者。本文…...
MySQL卸载 - Windows版
MySQL卸载 - Windows版 1. 停止MySQL服务 winR 打开运行,输入 services.msc 点击 “确定” 调出系统服务。 2. 卸载MySQL相关组件 打开控制面板 —> 卸载程序 —> 卸载MySQL相关所有组件 3. 删除MySQL安装目录 4. 删除MySQL数据目录 数据存放目录是在 …...
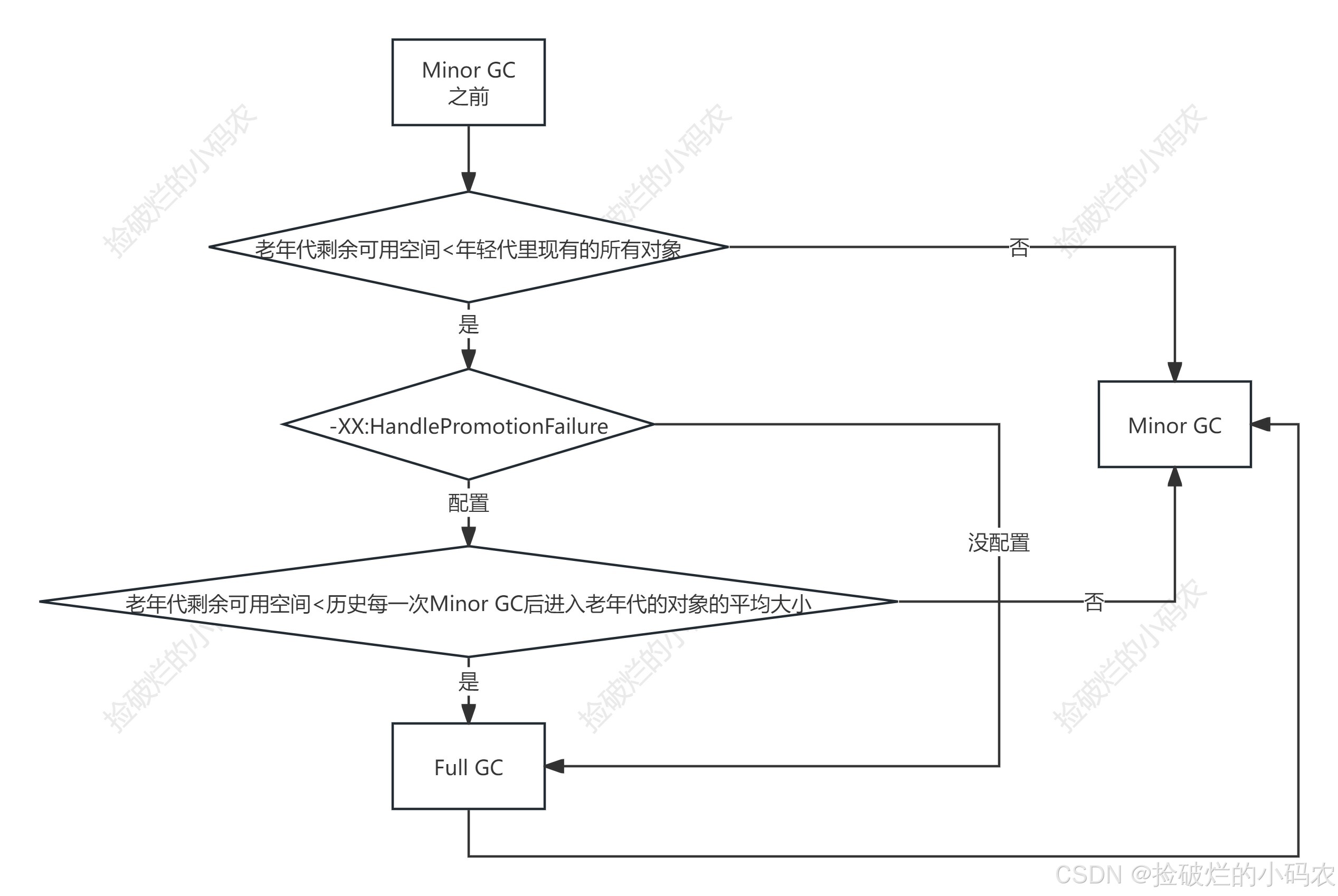
Java核心篇之JVM探秘:对象创建与内存分配机制
系列文章目录 第一章 Java核心篇之JVM探秘:内存模型与管理初探 第二章 Java核心篇之JVM探秘:对象创建与内存分配机制 第三章 Java核心篇之JVM探秘:垃圾回收算法与垃圾收集器 第四章 Java核心篇之JVM调优实战:Arthas工具使用及…...

Nuxt框架中内置组件详解及使用指南(五)
title: Nuxt框架中内置组件详解及使用指南(五) date: 2024/7/10 updated: 2024/7/10 author: cmdragon excerpt: 摘要:本文详细介绍了Nuxt框架中和组件的使用方法与配置,包括安装、基本用法、属性详解、示例代码以及高级功能如…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...

算法打卡第18天
从中序与后序遍历序列构造二叉树 (力扣106题) 给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。 示例 1: 输入:inorder [9,3,15,20,7…...

Visual Studio Code 扩展
Visual Studio Code 扩展 change-case 大小写转换EmmyLua for VSCode 调试插件Bookmarks 书签 change-case 大小写转换 https://marketplace.visualstudio.com/items?itemNamewmaurer.change-case 选中单词后,命令 changeCase.commands 可预览转换效果 EmmyLua…...

webpack面试题
面试题:webpack介绍和简单使用 一、webpack(模块化打包工具)1. webpack是把项目当作一个整体,通过给定的一个主文件,webpack将从这个主文件开始找到你项目当中的所有依赖文件,使用loaders来处理它们&#x…...

SOC-ESP32S3部分:30-I2S音频-麦克风扬声器驱动
飞书文档https://x509p6c8to.feishu.cn/wiki/SKZzwIRH3i7lsckUOlzcuJsdnVf I2S简介 I2S(Inter-Integrated Circuit Sound)是一种用于传输数字音频数据的通信协议,广泛应用于音频设备中。 ESP32-S3 包含 2 个 I2S 外设,通过配置…...

软件工程教学评价
王海林老师您好。 您的《软件工程》课程成功地将宏观的理论与具体的实践相结合。上半学期的理论教学中,您通过丰富的实例,将“高内聚低耦合”、SOLID原则等抽象概念解释得十分透彻,让这些理论不再是停留在纸面的名词,而是可以指导…...
