冒泡,选择,插入,希尔排序
目录
一. 冒泡排序
1. 算法思想
2. 时间复杂度与空间复杂度
3. 代码实现
二. 选择排序
1. 算法思想
2. 时间复杂度与空间复杂度
3. 代码实现
三.插入排序
1. 直接插入排序
(1). 算法思想
(2). 时间复杂度与空间复杂度
(3). 代码实现
2. 希尔排序
(1). 算法思想
(2). 代码实现
(3). 时间复杂度与空间复杂度
一. 冒泡排序
1. 算法思想
假设排升序,从头开始两两比较选出最大的的值移到最后面(假设下标为10),再从头开始两两比较选出次大的移到下标为9的地方以此类推

2. 时间复杂度与空间复杂度
(1). 最优情况
当数据全都有序时,最快。因为此时每个元素只需比较一次就可以完成整个排序过程此时时间复杂度为 O(N)
(2). 最坏情况
当数据逆序时最慢,此时每一次比较都需要交换。时间复杂度为 O(N²)
(3). 平均情况
综上所述,平均复杂度为 O(N²)
(4). 空间复杂度
冒泡排序只需要一个额外变量来交换元素,不需要额外的数据结构来存储数据,所以空间复杂度为 O(1)
3. 代码实现
void BubbleSort(int* a, int n)//冒泡排序
{int count = 0;for(int j=0;j<n-1;j++){for (int i = 0; i < n - j-1; i++){if (a[i] <a[i+1] ){Swap(&a[i], &a[i + 1]);count = 1;}}if (count == 0)break;}
}二. 选择排序
1. 算法思想
假设排升序,遍历数组,选出最大值与排序数列的最后一个元素(假设下标为10)交换,再从除最后一个元素(即下标0~9)的序列中找出次大值与下标为9的序列交换以此往复知道排序完毕
2. 时间复杂度与空间复杂度
(1). 时间复杂度
选择排序需要遍历n-1次来找到最小(或最大)元素,并且在每次遍历中都需要对剩余未排序元素进行遍历以找到最小(或最大)元素,因此选择排序的时间复杂度总是 O(N²)
(2) 空间复杂度
只需一个额外变量来存储找到的最大(或最小)元素的索引,所以空间复杂度为 O(1)
3. 代码实现
我们实现一个优化版本,同时找到最大的值与最小的值,分别与头和尾交换
void SelectSort(int* a, int n)
{int begin = 0, end = n -1;while(begin<end){int max = begin, min = begin;for (int i = begin+1; i <= end; i++){if (a[i] > a[max])max = i;if (a[i] < a[min])min = i;}Swap(&a[begin], &a[max]);Swap(&a[end], &a[min]);begin++;end--;}
}以上代码还有一个小问题,当出现下图情况时

begin所指向的值与max所指向的值交换,那min指向的值就变为了原来max所指向的值,此时再与end交换会发生将最大的值交换过去的情况
修改代码为
void SelectSort(int* a, int n)
{int begin = 0, end = n -1;while(begin<end){int max = begin, min = begin;for (int i = begin+1; i <= end; i++){if (a[i] > a[max])max = i;if (a[i] < a[min])min = i;}if (begin == min){Swap(&a[begin], &a[max]);Swap(&a[max], &a[end]);}else{Swap(&a[begin], &a[max]);Swap(&a[end], &a[min]);}begin++;end--;}
}三.插入排序
1. 直接插入排序
(1). 算法思想
从第一个元素开始排序,先排前一个数,再排前两个数以此类推
假设排升序,第一个数自然是有序的,第二个数与第一个数比较,如果比第一个数小就与其交换,然后看第三个数,此时前两个数是有序的,第三个数先于第二个数比较,比第二个数小就与其交换,再与第一个数比较,比第一个数小就与其交换,如果不比第二个数小就看第四个数,此时前三个数都是有序的以此类推

(2). 时间复杂度与空间复杂度
① 最好情况
在有序情况下只需遍历一遍即可时间复杂度为 O(N)
②最坏情况
在逆序情况下,每一次比较都要交换,时间复杂度为 O(N²)
③平均情况
综上所述平均时间复杂度为O(N²)
④空间复杂度
只需要一个额外的空间来存储当前要插入的元素,空间复杂度为O(1)
(3). 代码实现
void InsertSort(int* a,int n)//直接插入排序
{for(int i=0;i<n-1;i++){int end = i;int t = a[i+1];while (end >= 0){if (t < a[end]){a[end+1] = a[end];end--;}else break;}a[end+1] = t;}}2. 希尔排序
(1). 算法思想
是直接插入算法的改进版本,总体操作可大致分为两步
先进行预排序
直接插入排序
直接插入排序是和距离为1的元素比较,而希尔排序是和距离为gap的元素比较,gap不断变小,直到变为1,此时即是直接插入排序
初始序列为 9 1 2 5 7 4 8 6 3 5 ,gap值为5进行一次预排序过程如下

预排序后序列为

当gap为2时
预排序后序列为

我们发现预排序后一定比之前更加接近有序
从时间上讲,gap越大,大的数可以越快的到后面去,小的数可以越快的到前面去
gap越小呢,预排序完就越接近有序,gap==1就是直接插入排序
我们就可以将gap慢慢减少直到变为1从而进行直接插入排序是尽量是最好的情况
(2). 代码实现
希尔排序的代码与直接插入排序的代码十分相似,不同的地方就是gap,可以通过三层循环或四层循环实现,两者执行的次数实际是一样的
void ShellSort(int* a, int n)//希尔排序
{int gap = n;while(gap>1){gap =gap/ 3+1;// 除3不一定会=1,但3是最合理的,所以+1保证最后一次gap一定是1 //for(int j=0;j<gap;j++)//{for (int i = 0; i < n - gap; i++)//一组一组的排序所以i也可以+=gap,效率没有区别,都是要走这些步数{int end = i;int t = a[end + gap];while (end >= 0){if (t < a[end]){a[end + gap] = a[end];end -= gap;}elsebreak;}a[end + gap] = t;}//}}
}(3). 时间复杂度与空间复杂度
希尔时间复杂度的计算,需要很高的数学水平,此处只做粗略解释(我不会,嘿嘿)
①时间复杂度
我们假设每一次gap=n/3,此时每组三个数据,
最坏情况下 第一次排序消耗:(1+2)*n/3==n
下一次
gap=n/3/3=n/9,每组9个数据
但此时由于上面的预排序,不可能是最坏情况,即
(1+2+3+4+5+6+7+8)*n\9
具体计算我也不会
但是最后一次,gap==1时(此时很接近有序)
直接插入排序消耗n
时间复杂度大致为 O(N^1.3)即N的1.3次方
②空间复杂度
由于不需要额外的空间,所以空间复杂度为O(1)
这篇文章就到这里啦
(๑′ᴗ‵๑)I Lᵒᵛᵉᵧₒᵤ❤
相关文章:

冒泡,选择,插入,希尔排序
目录 一. 冒泡排序 1. 算法思想 2. 时间复杂度与空间复杂度 3. 代码实现 二. 选择排序 1. 算法思想 2. 时间复杂度与空间复杂度 3. 代码实现 三.插入排序 1. 直接插入排序 (1). 算法思想 (2). 时间复杂度与空间复杂度 (3). 代码实现 2. 希尔排序 (1). 算法思想 …...

【HarmonyOS学习】Calendar Kit日历管理
简介 Calendar Kit提供日历与日程管理能力,包括日历的获取和日程的创建能力。 Calendar Kit为用户提供了一系列接口来获取日历账户,并使用特定的接口向日历账户中写入日程。 如果写入的日程带有提醒时间则系统会在时间到达时向用户发送提醒。 约束点…...

RDMA 高性能架构基本原理与设计方案
RDMA的主要优点包括低延迟、高吞吐量、减少CPU负担和支持零拷贝网络。它允许数据直接在网络接口卡(NIC)和内存之间传输,减少了数据传输过程中的中间环节,从而显著降低了延迟。RDMA技术能够实现高速的数据传输,适用于需…...

【Springboot】事件机制发布与订阅的使用实践
文章目录 为什么要使用事件监听机制概念和原理使用场景用户注册系统实践案例1. 创建事件类2. 发布事件3. 监听事件3.1 通过注解EventListener实现监听3.2 通过实现ApplicationListener接口实现监听 4. 测试事件机制 总结 为什么要使用事件监听机制 在Springboot中,…...
新版网页无插件H.265播放器EasyPlayer.js如何测试demo视频?
H5无插件流媒体播放器EasyPlayer属于一款高效、精炼、稳定且免费的流媒体播放器,可支持多种流媒体协议播放,支持H.264与H.265编码格式,性能稳定、播放流畅;支持WebSocket-FLV、HTTP-FLV,HLS(m3u8࿰…...

PXE、Kickstart和cobbler
一.系统装机 1.1 三种引导方式 启动操作系统 1.硬盘 2.光驱(u盘) 3.网络启动 pxe 1.2 系统安装过程 1.加载boot loader: Boot Loader 是在操作系统内核运行之前运行的一段小程序。通过这段小程序,我们可以初始化硬件设 备、建立内存空间的映射图,从而将系统的软硬…...

【GameFramework扩展应用】6-3、GameFramework框架增加日志保存功能
推荐阅读 CSDN主页GitHub开源地址Unity3D插件分享简书地址QQ群:398291828大家好,我是佛系工程师☆恬静的小魔龙☆,不定时更新Unity开发技巧,觉得有用记得一键三连哦。 一、前言 【GameFramework框架】系列教程目录: https://blog.csdn.net/q764424567/article/details/1…...

将独热码应用到神经网络中
引言 接上回,本文继续说如何用TensorFlow将独热编码应用到一个简单的神经网络中,以实现从一段随机文本到另一段随机文本的转换。 步骤一:导入库 import tensorflow as tf import numpy as np import random import string步骤二࿱…...

在CSS中,使用Flexbox布局时,可以通过几个属性来控制容器内的项目之间的间距
display弹性布局,flex:1是占据剩下的空间 关于displa:flex /* 水平和垂直居中,水平和垂直方向上的间距均匀分布 / .container { display: flex; justify-content: space-between; / 左右对齐 / align-items: center; / 上下间距 */ flex-direction: ro…...

关于HDFS 和HBase
Apache HBase 被设计为在 Hadoop 分布式文件系统 (HDFS) 上运行的一个特殊类型的数据库。大白话: 想象一下,你有一个巨大的图书馆,这个图书馆就像 HDFS,它的架子上堆满了各种各样的书籍,每本书都非常厚,而…...

【HarmonyOS】HarmonyOS NEXT学习日记:二、ArkTs语法
【HarmonyOS】HarmonyOS NEXT学习日记:二、ArkTs语法 众所周知TS是JS的超集,而ArkTs则可以理解为是Ts的超集。他们的基础都基于JS,所以学习之前最好就JS基础。我的学习重点也是放在ArkTs和JS的不同点上。 文章主要跟着官方文档学习,跳过了一…...

Web前端-Web开发CSS基础2-选择器
一. 基础 1. 选中所有的<p>标签; 2. 选中所有的<ol>标签; 3. 选中所有的<ul>标签; 4. 选中所有id为happy的标签; 5. 选中所有id为sad的标签; 6. 选中所有id为angry的标签; 7. 选中所有类…...
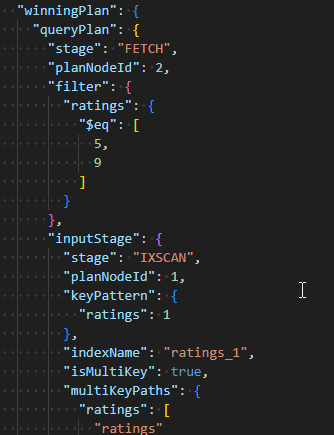
Mongodb数组字段索引之多键索引
学习mongodb,体会mongodb的每一个使用细节,欢迎阅读威赞的文章。这是威赞发布的第92篇mongodb技术文章,欢迎浏览本专栏威赞发布的其他文章。如果您认为我的文章对您有帮助或者解决您的问题,欢迎在文章下面点个赞,或者关…...

[Spring] Spring Web MVC案例实战
🌸个人主页:https://blog.csdn.net/2301_80050796?spm1000.2115.3001.5343 🏵️热门专栏: 🧊 Java基本语法(97平均质量分)https://blog.csdn.net/2301_80050796/category_12615970.html?spm1001.2014.3001.5482 🍕 Collection与…...

大模型“重构”教育:解构学习奥秘,推动教育普惠
大模型“重构”千行百业系列选题 生成式人工智能的热潮,为AI领域的发展注入新的活力,而“赋能千行百业”已经成为人们普遍对于人工智能和大模型的全新理解。 人工智能和大模型技术的迅猛发展正在以前所未有的速度深刻改变着各个行业。正如专家所预测&a…...

HCNA VRP基础
交换机可以隔离冲突域,路由器可以隔离广播域,这两种设备在企业网络中应用越来越广泛。随着越来越多的终端接入到网络中,网络设备的负担也越来越重,这时网络设备可以通过专有的VRP系统来提升运行效率。通过路由平台VRP是华为公司数…...

单片机外围设备-EEPROM
eeprom用iic通信。eeprom有几个特点需要关注: 1、可以单字节读写 2、eeprom按页划分存储,不同型号的eeprom的页大小不一致,往eeprom写数据时,如果写到了该页的末尾,会自动从该页的开头继续写,把之前的数据…...
YOLO--置信度(超详细解读)
YOLO(You Only Look Once)算法中的置信度(Confidence)是一个关键概念,用于评估模型对预测框内存在目标对象的信心程度以及预测框对目标对象位置的准确性。 一、置信度的定义 数值范围:置信度是一个介于0和…...

“解锁物流新纪元:深入探索‘沂路畅通‘分布式协作平台“
"解锁物流新纪元:深入探索沂路畅通分布式协作平台" 在21世纪的数字浪潮中,物流行业作为连接生产与消费的关键纽带,其重要性不言而喻。然而,随着市场规模的持续扩大和消费者需求的日益多样化,传统物流模式已…...

昇思25天学习打卡营第六天|应用实践/计算机视觉/Vision Transformer图像分类
心得 运行模型似乎有点靠天意?每次跑模型之前先来个焚香沐浴?总之今天是机器视觉的最后一课了,尽管课程里强调模型跑得慢,可是我的这次运行,居然很快的就看到结果了。 如果一直看我这个系列文章的小伙伴,…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

USB Over IP专用硬件的5个特点
USB over IP技术通过将USB协议数据封装在标准TCP/IP网络数据包中,从根本上改变了USB连接。这允许客户端通过局域网或广域网远程访问和控制物理连接到服务器的USB设备(如专用硬件设备),从而消除了直接物理连接的需要。USB over IP的…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...

LangChain知识库管理后端接口:数据库操作详解—— 构建本地知识库系统的基础《二》
这段 Python 代码是一个完整的 知识库数据库操作模块,用于对本地知识库系统中的知识库进行增删改查(CRUD)操作。它基于 SQLAlchemy ORM 框架 和一个自定义的装饰器 with_session 实现数据库会话管理。 📘 一、整体功能概述 该模块…...

iview框架主题色的应用
1.下载 less要使用3.0.0以下的版本 npm install less2.7.3 npm install less-loader4.0.52./src/config/theme.js文件 module.exports {yellow: {theme-color: #FDCE04},blue: {theme-color: #547CE7} }在sass中使用theme配置的颜色主题,无需引入,直接可…...

WebRTC从入门到实践 - 零基础教程
WebRTC从入门到实践 - 零基础教程 目录 WebRTC简介 基础概念 工作原理 开发环境搭建 基础实践 三个实战案例 常见问题解答 1. WebRTC简介 1.1 什么是WebRTC? WebRTC(Web Real-Time Communication)是一个支持网页浏览器进行实时语音…...

windows系统MySQL安装文档
概览:本文讨论了MySQL的安装、使用过程中涉及的解压、配置、初始化、注册服务、启动、修改密码、登录、退出以及卸载等相关内容,为学习者提供全面的操作指导。关键要点包括: 解压 :下载完成后解压压缩包,得到MySQL 8.…...
