算法2--贪心算法
1.老鼠和猫的交易
小老鼠准备了M磅的猫粮,准备去和看守仓库的猫做交易,因为仓库里有小老鼠喜欢吃的五香豆。
仓库有N个房间;
第i个房间有 J[i] 磅的五香豆,并且需要用 F[i] 磅的猫粮去交换;
老鼠不必交换该房间所有的五香豆,换句话说,它可以用 F[i] * a% 磅的猫粮去换取 J[i] * a% 磅的五香豆,其中a是一个实数。现在,请帮忙计算一下,小老鼠最多能够得到多少磅的五香豆?
输入描述
输入包含多组测试用例。
每组测试数据首先一行是2个非负整数 M 和 N ,接着的 N 行,每行分别包含2个非负整数 J[i] 和 F[i] 。
输入数据以两个-1结束。
题目保证所有的数据不超过1000。输出描述
请计算并输出小老鼠最多能够得到的五香豆数量。
每组数据输出一行,保留3位小数。用例输入 1
5 3 7 2 4 3 5 2 20 3 25 18 24 15 15 10 -1 -1用例输出 1
13.333 31.500
学习:http://t.csdnimg.cn/gcmty
#include<bits/stdc++.h>
using namespace std;
int i;
int m,n;//猫粮数,房间数
double tot=0;//换后的奶酪数
struct room{double food;double cheese;
}a[100000];//数组开大一点 //sort函数的函数部分,从大到小排序
bool cmp(room x,room y)
{return (x.cheese)/x.food>(y.cheese)/y.food;
}int main()
{while(scanf("%d %d",&m,&n)!=EOF){if(m==-1&&n==-1) break;//结束条件 for(i=1;i<=n;i++)cin>>a[i].cheese>>a[i].food;//读入奶酪和猫粮 sort(a+1,a+1+n,cmp);//注意首地址 for(i=1;i<=n;i++){if(m-a[i].food>=0)//猫粮多于一只猫需要的猫粮 {tot=tot+1.0*a[i].cheese;//老鼠得到奶酪增加 m=m-a[i].food;//老鼠手中猫粮减少 }else//按比例购买最后一份猫粮 {tot=tot+1.0*a[i].cheese/a[i].food*m;break;} }printf("%.3lf\n",tot);tot=0;//注意结束后清零 }return 0;
}2.田忌赛马
“田忌赛马”是中国历史上一个著名的故事。
大约2300年前,齐国大将田忌喜欢和国王赛马,并且约定:每赢一场,对方就要付200元。
假设已知田忌和国王的各自马匹的速度都不相同,请计算田忌最好的结果是什么。
输入描述
输入包含多组测试样例。
每组样例的第一行是一个整数n(n <= 1000),表示田忌和国王各自参赛的马匹数量。
接下来一行的n个整数表示田忌的马的速度,再接下来一行的n个整数表示国王的马的速度。
n为0时,表示输入数据的结束。输出描述
每组数据输出一行,表示田忌最多能够赢得的金额。
用例输入 1
3 92 83 71 95 87 74 2 20 19 22 18 0用例输出 1
200 0
一篇非常详细的文章:http://t.csdnimg.cn/qQPsV
题目分析:田忌赛马是一种权衡取舍,找适合策略,来收获最大利益的问题。在本题中我们先将田忌与齐王的马进行排序(在此,我以降序排序),然后选择最优解(比较快马):
1、田忌>齐王:正常比赛。
2、田忌<齐王:田忌慢马与齐王快马比赛。以慢换快
3、田忌=齐王(这一点十分容易忽略):这时我们可以观察慢马,若此时田忌>齐王,可以直接让慢马比赛(无疑时必赢的)。若此时田忌<=齐王,将田忌慢马与齐王快马比赛(与慢马或快马进行比赛,都是不可能赢的,何不换取更大的利益)。
#include<bits/stdc++.h>
using namespace std;//sort函数的函数部分,从大到小排序
bool cmp(int x,int y)
{return x>y;
}int main()
{int n,a[10000],b[10000];while(scanf("%d",&n)!=EOF){if(n==0) break; int i,j;for(i=0;i<n;i++) cin>>a[i];for(i=0;i<n;i++) cin>>b[i];//从快到慢排序 sort(a,a+n,cmp);sort(b,b+n,cmp);int l1=0,l2=0,sum=0;//排序后的左侧快马 int r1=n-1,r2=n-1;//排序后的右侧慢马 for(i=0;i<n;i++){if(a[l1]>b[l2])//快马:田忌 >齐王 ,正常比赛就可以赢 {l1++;l2++;sum++;}else if(a[l1]<b[l2])//快马:田忌<齐王 ,田忌慢马和齐王快马比赛,包输的 {r1--;l2++;sum--;}else if(a[r1]>b[r2])//快马相等,慢马田忌>齐王 ,正常比赛就赢了 {r1--;r2--;sum++;}else if(a[r1]<b[l2])//快马相等,慢马田忌<=齐王 ,田忌慢和齐王快比赛,包输的 {r1--;l2++;sum--;}}cout<<sum*200<<endl;}return 0;
}3.搬桌子
丁爸信奥培训中心最近在富丽科技大厦租了一层楼,这层楼的形状如下:
由图可见,这层楼中间是走廊,两侧各有200个房间,编号如上图。最近,丁爸信奥培训中心做了内部机构的调整,需要把一些桌子从一个房间搬到另外的房间。因为走廊很窄,但是桌子很大,所以同一段走廊每次只能通过一个桌子。
假设不论远近,每趟搬桌子都需要10分钟。同时,当你从房间i搬桌子到房间j的过程中,房间i到房间j之间的走廊都被占用,也就是说,在每个10分钟内,不能有多个任务共享同一段走廊。
现在,丁爸想知道:要完成所有的搬运任务,最少需要多少时间?
输入描述
输入包含T组测试用例。
每组测试用例首先是一个正整数N(1<=N<=200),表示需要搬运的桌子数量。
接下来N行,每行包含2个正整数s和t,表示需要将一个桌子从房间s搬到房间t。输出描述
计算并输出完成所有的搬运任务需要的最少的时间,每组数据占一行。
用例输入 1
3 4 10 20 30 40 50 60 70 80 2 1 3 2 200 3 10 100 20 80 30 50用例输出 1
10 20 30
1. 我们可以把走廊模拟成一条线段,搬运桌子的起始位置模拟成这条线段上的区间;
2. 要想用时尽可能的少,我们应当让在同一时间段搬运的桌子尽可能多,也就是同一时间段线段上互不相交的区间尽可能多;
3. 对于那些存在重叠的区间,我们别无他法,只能分在不同时间段搬运;
4. 因此,我们需要找到区间之间的最大重叠次数,就是我们至少需要的时间;
注意点:由于房间分为两排,1和2, 3和4对应着同一段走廊,所以我们需要通过映射,把房间号对应成相应的走廊号。
#include<bits/stdc++.h>
using namespace std;
int main()
{int i,j,n,t,p[201];int s,d,temp,k,max;cin>>t;while(t--){for(i=0;i<=200;i++) p[i]=0;//初识化 cin>>n;for(i=0;i<n;i++){cin>>s>>d;//使房间1和2对应的是一个位置 s=(s-1)/2;d=(d-1)/2;//从号码大的房间往回搬的情况if(s>d) {temp=s;s=d;d=temp;}for(k=s;k<=d;k++) p[k]++;}max=-1;for(i=0;i<=200;i++){if(p[i]>max) max=p[i];//通过某个地方最大次数为最小时间 }cout<<max*10<<endl;} return 0;
}4.今年暑假不AC
作为球迷,一定想看尽量多的完整的比赛,当然,作为新时代的好青年,你一定还会看一些其它的节目,比如新闻联播(永远不要忘记关心国家大事)、非常6+7、超级女生,以及王小丫的《开心辞典》等等,假设你已经知道了所有你喜欢看的电视节目的转播时间表,你会合理安排吗?(目标是能看尽量多的完整节目)
输入描述
输入数据包含多个测试实例,每个测试实例的第一行只有一个整数n(n<=100),表示你喜欢看的节目的总数,然后是n行数据,每行包括两个数据Tis,Tie (1<=i<=n),分别表示第i个节目的开始和结束时间,为了简化问题,每个时间都用一个正整数表示。n=0表示输入结束,不做处理。
输出描述
对于每个测试实例,输出能完整看到的电视节目的个数,每个测试实例的输出占一行。
用例输入 1
12 1 3 3 4 0 7 3 8 15 19 15 20 10 15 8 18 6 12 5 10 4 14 2 9 0用例输出 1
5
若干个电视节目,自样例:按结束时选择合适然要按时间顺序来看。为了看更多的节目,需要尽
快看完一个节目再看另外一个节目,多看短节目才能看更多的节目。
此题贪心的原则是,选择结束时间早的节目,留出时间看更多的节目。因此需要根据节目结束时间排序。
一开始,lastend=count=0,,循环i=0不对,然后改了一下,过了
#include<bits/stdc++.h>
using namespace std;
typedef struct node
{int start;int end;
}schedule;bool cmp(schedule x,schedule y)
{return x.end<y.end;
}int main()
{int i,n;schedule s[100000];while(scanf("%d",&n)!=EOF){if(n==0) break;for(i=0;i<n;i++)cin>>s[i].start>>s[i].end;sort(s,s+n,cmp);int lastend=s[0].end;int count=1;for(i=1;i<n;i++){if(s[i].start>=lastend){count++;lastend=s[i].end;}}cout<<count<<endl;}return 0;
}5.奋勇争先续
还记得上次那个奋勇争先的题目吗,聪明的你帮助老师找出了第一名的同学。
现在,有个类似的问题:
已知每一位同学的解题数量和罚时,这次希望你能输出排名靠前的若干同学的名单。注:排名首先依据做题数量,若做题数量相同,则比较罚时,罚时少的排名靠前。
输入描述
第一行是数据组数C,代表有C组测试实例。
每一组数据第一行两个整数N和M,N代表有N个人的成绩,M表示老师需要你输出前M名的名单。
接下来N行,每一行依次给出名字Name,做出的题目数量num和罚时time
( 1<=C<=10, 2<M<=N<=1000, Name的长度最大为10,1<=num<=10, 10<=time<=100000 )输出描述
每组测试数据输出M行,第i行为第i名的名字、解题数量和罚时,中间用空格隔开。
每组数据后空一行。
用例输入 1
1 3 3 Bob 5 50 Alice 4 46 John 5 48用例输出 1
John 5 48 Bob 5 50 Alice 4 46
#include<bits/stdc++.h>
using namespace std;
struct stu
{char name[100];int num;int time;
}s[1001];bool com(stu a,stu b)
{if(a.num<b.num) return a.num>b.num;//从大到小else if(a.num==b.num) return a.time<b.time;//从小到大
}int main()
{int t;cin>>t;while(t--){int n,m,i;cin>>n>>m;for(i=0;i<n;i++)scanf("%s%d %d",s[i].name,&s[i].num,&s[i].time);sort(s,s+n,com);for(i=0;i<m;i++)printf("%s %d %d\n",s[i].name,s[i].num,s[i].time);printf("\n"); }return 0;
} 6.Degree Sequence of Graph G
Wang Haiyang is a strong and optimistic Chinese youngster. Although born and brought up in the northern inland city Harbin, he has deep love and yearns for the boundless oceans. After graduation, he came to a coastal city and got a job in a marine transportation company. There, he held a position as a navigator in a freighter and began his new life.
The cargo vessel, Wang Haiyang worked on, sails among 6 ports between which exist 9 routes. At the first sight of his navigation chart, the 6 ports and 9 routes on it reminded him of Graph Theory that he studied in class at university. In the way that Leonhard Euler solved The Seven Bridges of Knoigsberg, Wang Haiyang regarded the navigation chart as a graph of Graph Theory. He considered the 6 ports as 6 nodes and 9 routes as 9 edges of the graph. The graph is illustrated as below.
According to Graph Theory, the number of edges related to a node is defined as Degree number of this node.
Wang Haiyang looked at the graph and thought, If arranged, the Degree numbers of all nodes of graph G can form such a sequence: 4, 4, 3,3,2,2, which is called the degree sequence of the graph. Of course, the degree sequence of any simple graph (according to Graph Theory, a graph without any parallel edge or ring is a simple graph) is a non-negative integer sequence?
Wang Haiyang is a thoughtful person and tends to think deeply over any scientific problem that grabs his interest. So as usual, he also gave this problem further thought, As we know, any a simple graph always corresponds with a non-negative integer sequence. But whether a non-negative integer sequence always corresponds with the degree sequence of a simple graph? That is, if given a non-negative integer sequence, are we sure that we can draw a simple graph according to it.?
Let’s put forward such a definition: provided that a non-negative integer sequence is the degree sequence of a graph without any parallel edge or ring, that is, a simple graph, the sequence is draw-possible, otherwise, non-draw-possible. Now the problem faced with Wang Haiyang is how to test whether a non-negative integer sequence is draw-possible or not. Since Wang Haiyang hasn’t studied Algorithm Design course, it is difficult for him to solve such a problem. Can you help him?
输入描述
The first line of input contains an integer T, indicates the number of test cases. In each case, there are n+1 numbers; first is an integer n (n<1000), which indicates there are n integers in the sequence; then follow n integers, which indicate the numbers of the degree sequence.
输出描述
For each case, the answer should be "yes"or “no” indicating this case is “draw-possible” or “non-draw-possible”.
用例输入 1
2 6 4 4 3 3 2 2 4 2 1 1 1用例输出 1
yes no
可图性的问题
sort()函数中的greater<int>()参数表示将容器内的元素降序排列。不填此参数,默认表示升序排列。
vector<int> a = {1,2,3};
sort(a.begin(), a.end(), greater<int>()); //将a降序排列
sort(a.begin(), a.end()); //将a升序排列
学习:http://t.csdnimg.cn/ENfbk
#include<bits/stdc++.h>
using namespace std;
int a[1006];int havel(int n);int main()
{int t;cin>>t;while(t--){int i,n,flag=0;cin>>n;for(i=0;i<n;i++) cin>>a[i];if(havel(n)==1) cout<<"yes"<<endl;else cout<<"no"<<endl;}return 0;
} int havel(int n)
{int i,j;for(i=0;i<n;i++){sort(a,a+n,greater<int>());//降序排序 if(a[0]==0) return 1;//数组全0退出 for(j=1;j<=a[0];j++){if(a[j]==0) return 0;//若为0,-1为负数无法构成简单图 else a[j]--;}a[0]=0;//当前点的度清零,会排在最后,不影响有度的点 }
}贪心算法:
在对问题求解时,总是作出在当前看来是最好的选择,也就是说,不从整体上加以考虑,所作出的仅仅是在某种意义上的局部最优解。
前提:排序。
最长的事件序列问题
可图性判定
1.度序列:若把图G所有顶点的度数排成一个序列S,则称S为图G的度序列。
2.序列是可图的:一个非负整数组成的有限序列如果是某个无向图的度序列,则称该序列是可图的。
Havel-Hakimi定理:,每趟都要排序。
sort函数
sort(首地址,尾地址+1,[cmp函数])
1.这个函数可以传两个或三个参数
2.第一个参数是要排序的区间首地址
3.第二个参数是区间尾地址的下一地址
4.第三个参数不写,则缺省为递增排序
若为从大到小排序
int类型
int num[100];
bool cmp(int a,int b)
{return a>b;
}
sort(num,num+100,cmp);结构体类型
struct node
{int a;double b;
}arr[100];
//先按照a值升序排列,若a值相同,再按b值降序排列。
bool cmp(node x,node y)
{if(x.a!=y.a)return x.a<y.a;return x.b>y.b;
}
sort(arr,arr+100,cmp);浮点数比较大小不要直接==
double score;
if(fabs(x.score-y.score)>0.00001return x.score>y.score;sort函数可以对数组的某一段进行排序。
若数组中元素是从下标1的位置开始存储,导致忘记修改sort的第一个参数。
相关文章:
算法2--贪心算法
1.老鼠和猫的交易 小老鼠准备了M磅的猫粮,准备去和看守仓库的猫做交易,因为仓库里有小老鼠喜欢吃的五香豆。 仓库有N个房间; 第i个房间有 J[i] 磅的五香豆,并且需要用 F[i] 磅的猫粮去交换; 老鼠不必交换该房间所有的五…...

本地部署 EVE: Unveiling Encoder-Free Vision-Language Models
本地部署 EVE: Unveiling Encoder-Free Vision-Language Models 0. 引言1. 快速开始2. 运行 Demo 0. 引言 EVE (Encoder-free Vision-language model) 是一种创新的多模态 AI 模型,主要特点是去除了传统视觉语言模型中的视觉编码器。 核心创新 架构创新ÿ…...

阿里云CDN- https(设计支付宝春节开奖业务)
HTTP相关概念 1. HTTP概述 http是最广泛的网络协议,是客户端与服务器之间的请求与应答的标准(TCP),用于www服务器传输超文本到本地浏览器的传输协议,使浏览器更加高效,网络传输减少。 2.HTTPS概述 http…...

为何众多卖家选择加入亚马逊VC平台?他们的决策依据是什么?
众多卖家选择加入亚马逊VC平台,其背后蕴含着深思熟虑的决策逻辑。亚马逊VC平台作为一个专门为品牌供应商打造的销售平台,具有一系列独特且引人注目的优势。 首先,VC平台为卖家提供了品牌控制力的增强。在这个平台上,卖家能够更直接…...

Windows与Linux双机热备软件推荐
网络数据安全在如今信息化的时代越来越变得举足轻重,因此服务器维护和管理也成为企业健康稳定运营的一项重要工作。但实际情况是很多公司并没有配备专业的运维人员,一般都会通过一些管理软件维护或者主机托管给服务商。整理6款服务器的Windows与Linux双机…...

Mysql基础与安装
一、数据库的概念和相关的语法和规范 1、数据库的概念 数据库:组织,存储,管理数据的仓库。 数据库的管理系统(DBMS):实现对数据有效组织,管理和存取的系统软件。 数据库的种类: m…...

线程的死锁和并发安全
在多线程编程中,线程的死锁和并发安全是两个重要的概念。理解这两个概念并正确地管理它们,对于编写高效且可靠的并发程序至关重要。 线程的死锁 死锁(Deadlock) 是指两个或多个线程相互等待对方释放已经持有的资源,导…...

docker 启动提示can not create sys fs cgroup cpuset....问题处理
docker 启动失败 报错 大概报错内容为 cgroup :no such file can not create /sys/fs/cgroup/cpuset … 问题是因为 /sys/fs/cgroup/ 没有被正确挂载 cgroup 是实现资源限制的工具 docker 能够进行限制cpu 内存 大小 依赖cgroup ll /sys/fs/cgroup/ 发现一个都系也没有 m…...

[C/C++入门][ifelse]19、制作一个简单计算器
简单的方法 我们将假设用户输入两个数字和一个运算符(、-、*、/),然后根据所选的运算符执行相应的操作。 #include <iostream> using namespace std;int main() {double num1, num2;char op;cout << "输入 (,-,*,/): &quo…...

API取数实战:企业微信API取数教程
在数字化时代,企业微信不仅是一个通讯工具,更是企业数字化转型的重要平台。通过企业微信,企业能够高效连接员工、客户与合作伙伴,实现内部流程的自动化和智能化。本文将介绍企业微信API的应用场景和应用难点,并提供企业…...
AI算法18-最小角回归算法Least Angle Regression | LARS
最小角回归算法简介 最小角回归(Least Angle Regression, LAR)是一种用于回归分析的统计方法,它在某些方面类似于最小二乘回归,但提供了一些额外的优点。最小角回归由Bradley Efron等人提出,主要用于处理具有…...

wordpress 调用另外一个网站的内容 按指定关键词调用
要在WordPress中调用另一个网站的内容并根据指定关键词进行筛选,你可以使用以下代码。这段代码使用了WordPress内置的wp_remote_get函数来获取远程网站的内容,然后使用PHP的DOMDocument和DOMXPath类来解析HTML并筛选出包含指定关键词的内容。 首先&…...

kotlin数据类型
人不走空 🌈个人主页:人不走空 💖系列专栏:算法专题 ⏰诗词歌赋:斯是陋室,惟吾德馨 Kotlin基本数值类型 基本数据类型包括 Byte、Short、Int、Long、Float、Double 整数类型 类型位宽最小值最大…...

[GWCTF 2019]babyvm
第一次接触VM逆向 先粘一下对我很有帮助的两篇佬的博客 系统学习vm虚拟机逆向_vmp 虚拟机代码逆向-CSDN博客 这篇去学习vm逆向到底是什么 我的浅显理解啊,就是和汇编的定义差不多,规定一个函数,用什么其他的名字 然后这道题 [GWCTF 2019]babyvm 详解 (vm逆向 …...

PyTorch论文
2019-12 PyTorch: An Imperative Style, High-Performance Deep Learning Library 设计迎合4大趋势: 1. array-based (Tensor) 2. GPU加速 3. 自动求导 (Auto Differentiation) 4. 拥抱Python生态 4大设计原则: 1. 使用算法和数据开发者熟悉的Python做编…...
【Python实战因果推断】37_双重差分8
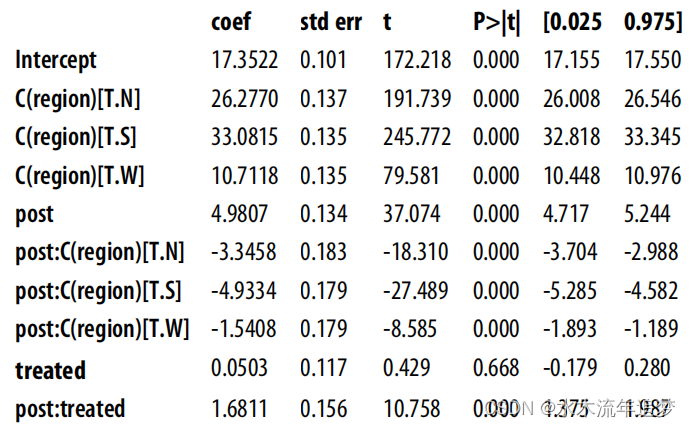
目录 Diff-in-Diff with Covariates Diff-in-Diff with Covariates 您需要学习的 DID 的另一个变量是如何在模型中包含干预前协变量。这在您怀疑平行趋势不成立,但条件平行趋势成立的情况下非常有用: 考虑这种情况:您拥有与之前相同的营销数…...

【python学习】第三方库之matplotlib的定义、功能、使用场景和代码示例(线图、直方图、散点图)
引言 Matplotlib 是一个 Python 的 2D 绘图库,它可以在各种平台上以各种硬拷贝格式和交互环境生成具有出版品质的图形。通过 Matplotlib,开发者可以仅需要几行代码,便可以生成绘图、直方图、功率谱、条形图、错误图、散点图等 Matplotlib 是 …...

MySQL(3)表的操作
目录 1. 表的操作; 2. 数据类型; 1. 表的操作: 1.1 创建表: 语法: create table 表名( 属性 类型 [comment ], 属性 类型 [comment ], 属性 类型 ) character set 字符集 collate 校验集 engine 存储引擎; 前面博客提到: MyISAM和InoDB这两个比较重要. 1.2 查看表…...

SQL GROUPING运算符详解
在大数据开发中,我们经常需要对数据进行分组和汇总分析。 目录 1. GROUPING运算符概念2. 语法和用法3. 实际应用示例4. GROUPING运算符的优势5. 高级应用场景5.1 与CASE语句结合使用5.2 多维数据分析 6. 性能考虑和优化技巧7. GROUPING运算符的局限性8. 最佳实践9. GROUPING与其…...

在VS2017下FFmpeg+SDL编写最简单的视频播放器
1.下载ShiftMediaProject/FFmpeg 2.下载SDL2 3.新建VC控制台应用 3.配置include和lib 4.把FFmpeg和SDL的dll 复制到工程Debug目录下,并设置调试命令 5.复制一下mp4视频到工程Debug目录下(复制一份到*.vcxproj同一目录,用于调试) 6…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

从“安全密码”到测试体系:Gitee Test 赋能关键领域软件质量保障
关键领域软件测试的"安全密码":Gitee Test如何破解行业痛点 在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的"神经中枢"。从国防军工到能源电力,从金融交易到交通管控,这些关乎国计民生的关键领域…...

