LabVIEW 与 PLC 通讯方式
在工业自动化中,LabVIEW 与 PLC(可编程逻辑控制器)的通信至关重要,常见的通信方式包括 OPC、Modbus、EtherNet/IP、Profibus/Profinet 和 Serial(RS232/RS485)。这些通信协议各有特点和应用场景,选择合适的协议能显著提升系统的效率和可靠性。例如,OPC 适用于复杂的自动化系统,提供实时数据访问和控制,而 Modbus 则因其简单易用和开放标准广泛用于设备监控。
-
OPC(OLE for Process Control)
-
特点:通用性强,支持多种品牌的 PLC;易于集成和扩展;实时数据访问。
-
应用:适用于复杂的工业自动化系统。
-
-
Modbus
-
特点:简单易用,开放标准,支持多种设备;适用于串行和以太网通信。
-
应用:常用于较小的自动化系统和设备监控。
-
-
EtherNet/IP
-
特点:基于以太网的工业协议,高速可靠,支持大规模数据传输。
-
应用:大型自动化系统和实时控制。
-
-
Profibus/Profinet
-
特点:西门子开发的工业总线协议,支持高速通信和大规模设备集成。
-
应用:主要用于西门子 PLC 和大型自动化项目。
-
-
Serial(RS232/RS485)
-
特点:成本低,简单易用;适用于短距离通信和点对点连接。
-
应用:小型系统和设备通信。
-
比较表
| 通讯方式 | 特点 | 应用场景 |
|---|---|---|
| OPC | 通用性强,易集成,实时数据 | 复杂工业自动化系统 |
| Modbus | 开放标准,简单易用,支持多设备 | 小型自动化系统和设备监控 |
| EtherNet/IP | 高速可靠,大规模数据传输 | 大型自动化系统和实时控制 |
| Profibus/Profinet | 高速通信,大规模设备集成 | 西门子 PLC,大型项目 |
| Serial | 成本低,简单易用,短距离通信 | 小型系统和点对点连接 |
使用方法
-
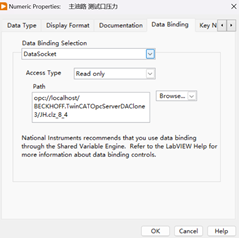
配置 OPC 服务器:在 LabVIEW 中设置 OPC 服务器地址和路径。
-
DataSocket 绑定:在 LabVIEW 中使用 DataSocket 进行数据绑定,指定 OPC 路径。
-
读取/写入数据:使用 LabVIEW 的读写函数进行实时数据访问和控制。
通过以上方式,LabVIEW 能够与多种 PLC 设备进行高效通信,适用于各种工业自动化应用。
相关文章:

LabVIEW 与 PLC 通讯方式
在工业自动化中,LabVIEW 与 PLC(可编程逻辑控制器)的通信至关重要,常见的通信方式包括 OPC、Modbus、EtherNet/IP、Profibus/Profinet 和 Serial(RS232/RS485)。这些通信协议各有特点和应用场景,…...

数据结构初阶·排序算法(内排序)
目录 前言: 1 冒泡排序 2 选择排序 3 插入排序 4 希尔排序 5 快速排序 5.1 Hoare版本 5.2 挖坑法 5.3 前后指针法 5.4 非递归快排 6 归并排序 6.1递归版本归并 6.2 非递归版本归并 7 计数排序 8 排序总结 前言: 目前常见的排序算法有9种…...

PL/SQL oracle上多表关联的一些记录
1.记录自己在PL/SQL上写的几张表的关联条件没有跑出来的一些优化 1. join后面跟上筛选条件 left join on t1.id t2.id and --- 带上分区字段,如 t1.month 202405, 操作跑不出来的一些问题,可能是数据量过大,未做分区过滤 2. 创建…...

Java.Net.UnknownHostException:揭开网络迷雾,解锁异常处理秘籍
在Java编程的浩瀚宇宙中,java.net.UnknownHostException犹如一朵不时飘过的乌云,让开发者在追求网络畅通无阻的道路上遭遇小挫。但别担心,今天我们就来一场说走就走的探险,揭秘这个异常的真面目,并手把手教你几招应对之…...

第十课:telnet(远程登入)
如何远程管理网络设备? 只要保证PC和路由器的ip是互通的,那么PC就可以远程管理路由器(用telnet技术管理)。 我们搭建一个下面这样的简单的拓扑图进行介绍 首先我们点击云,把云打开,点击增加 我们绑定vmn…...

【概率论三】参数估计:点估计(矩估计、极大似然法)、区间估计
文章目录 一. 点估计1. 矩估计法2. 极大似然法2.1. 似然函数2.2. 极大似然估计法 3. 评价估计量的标准3.1. 无偏性3.2. 有效性3.3. 一致性 二. 区间估计1. 区间估计的概念2. 正态总体参数的区间估计 参数估计讲什么 由样本来确定未知参数参数估计分为点估计与区间估计 一. 点估…...

自动化产线 搭配数据采集监控平台 创新与突破
自动化产线在现在的各行各业中应用广泛,已经是现在的生产趋势,不同的自动化生产设备充斥在各行各业中,自动化的设备会产生很多的数据,这些数据如何更科学化的管理,更优质的利用,就需要数据采集监控平台来完…...

【Karapathy大神build-nanogpt】Take Away Notes
B站翻译LINK Personal Note Andrej rebuild gpt2 in pytorch. Take Away Points Before entereing serious training, he use Shakespear’s work as a small debugging datset to see if a model can overfit. Overfitging is a should thing.If we use TF32 or BF32, (by…...

MySQL学习记录 —— 이십이 MySQL服务器日志
文章目录 1、日志介绍2、一般、慢查询日志1、一般查询日志2、慢查询日志FILE格式TABLE格式 3、错误日志4、二进制日志5、日志维护 1、日志介绍 中继服务器的数据来源于集群中的主服务。每次做一些操作时,把操作保存到重做日志,这样崩溃时就可以从重做日志…...
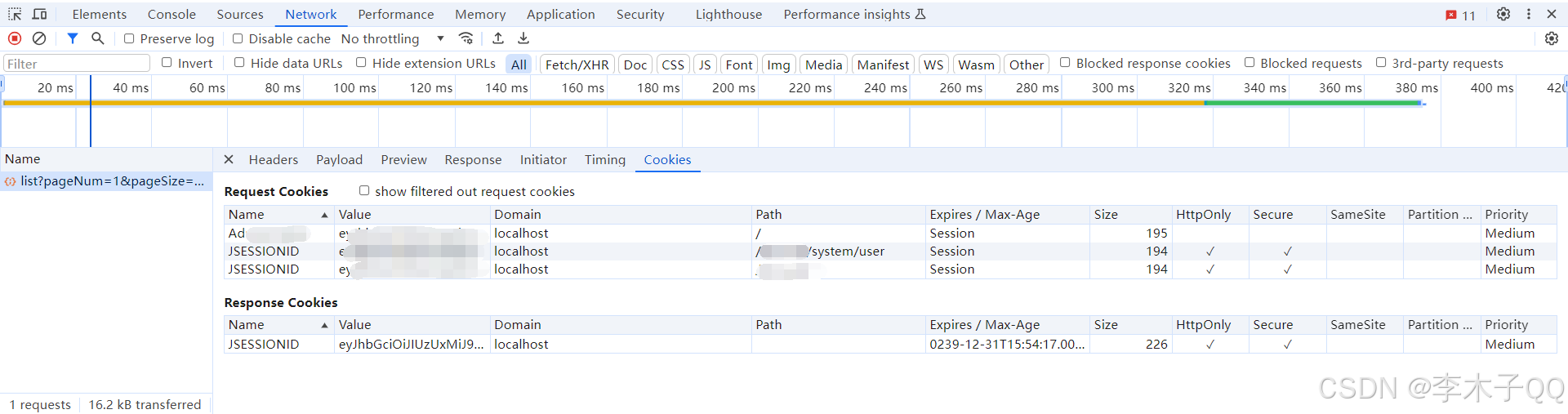
HTTPS请求头缺少HttpOnly和Secure属性解决方案
问题描述: 建立Filter拦截器类 package com.ruoyi.framework.security.filter;import com.ruoyi.common.core.domain.model.LoginUser; import com.ruoyi.common.utils.SecurityUtils; import com.ruoyi.common.utils.StringUtils; import com.ruoyi.framework.…...

react基础样式控制
行内样式 <div style{{width:500px, height:300px,background:#ccc,margin:200px auto}}>文本</div> class类名 注意:在react中使用class类名必须使用className 在外部src下新建index.css文件写入你的样式 .fontcolor{color:red } 在用到的页面引入…...
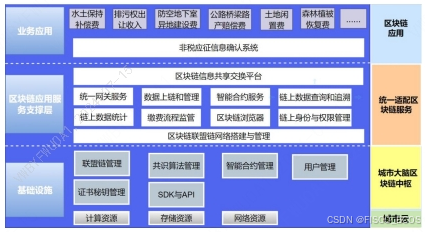
【区块链 + 智慧政务】涉税行政事业性收费“e 链通”项目 | FISCO BCOS应用案例
国内很多城市目前划转至税务部门征收的非税收入项目已达 17 项,其征管方式为行政主管部门核定后交由税务 部门征收。涉税行政事业性收费受限于传统的管理模式,缴费人、业务主管部门、税务部门、财政部门四方处于 相对孤立的状态,信息的传递靠…...

Socket、WebSocket 和 MQTT 的区别
Socket 协议 定义:操作系统提供的网络通信接口,抽象了TCP/IP协议,支持TCP和UDP。特点: 通用性:不限于Web应用,适用于各种网络通信。协议级别:直接使用TCP/UDP,需要手动管理连接和数…...
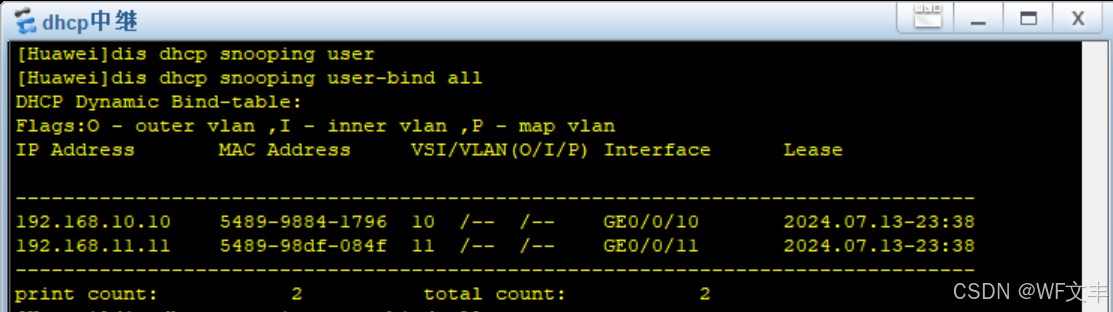
企业网络实验(vmware虚拟机充当DHCP服务器)所有IP全部保留,只为已知mac分配固定IP
文章目录 需求实验修改dhcp虚拟机配置文件测试PC获取IP查看user-bind 需求 (vmware虚拟机充当DHCP服务器)所有IP全部保留,只为已知mac分配固定IP 实验 前期配置: https://blog.csdn.net/xzzteach/article/details/140406092 后续配置均在以上配置的前…...
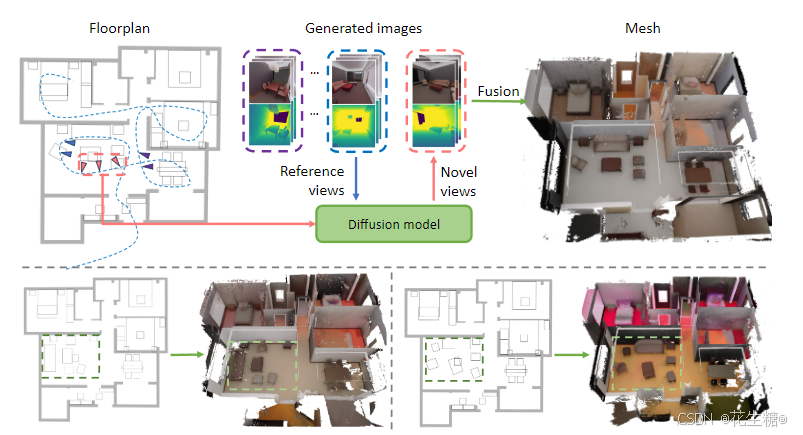
HouseCrafter:平面草稿至3D室内场景的革新之旅
在室内设计、房地产展示和影视布景设计等领域,将平面草稿图快速转换为立体的3D场景一直是一个迫切的需求。HouseCrafter,一个创新的AI室内设计方案,正致力于解决这一挑战。本文将探索HouseCrafter如何将这一过程自动化并提升至新的高度。 一、定位:AI室内设计的革新者 Ho…...
C#统一委托Func与Action
C#在System命名空间下提供两个委托Action和Func,这两个委托最多提供16个参数,基本上可以满足所有自定义事件所需的委托类型。几乎所有的 事件 都可以使用这两个内置的委托Action和Func进行处理。 Action委托: Action定义提供0~16个参数&…...

MongoDB 基本查询语句
基本查询 查询所有文档: db.collection.find()示例: db.users.find()按条件查询文档: db.collection.find({ key: value })示例: db.users.find({ age: 25 })查询并格式化输出: db.collection.find().pretty()示例&…...
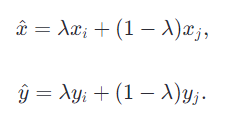
28_EfficientNetV2网络详解
V1:https://blog.csdn.net/qq_51605551/article/details/140487051?spm1001.2014.3001.5502 1.1 简介 EfficientNetV2是Google研究人员Mingxing Tan和Quoc V. Le等人在2021年提出的一种深度学习模型,它是EfficientNet系列的最新迭代,旨在提…...

PyCharm查看文件或代码变更记录
背景: Mac笔记本上有一个截图的定时任务在运行,本地Python使用的是PyCharm IDE,负责的同事休假,然后定时任务运行的结果不符合预期,一下子不知道问题出现在哪里。 定位思路: 1、先确认网络、账号等基本的…...

Java开发手册中-避免Random实例被多线程使用、多线程下Random与ThreadLoacalRandom性能对比
场景 Java中使用JMH(Java Microbenchmark Harness 微基准测试框架)进行性能测试和优化: Java中使用JMH(Java Microbenchmark Harness 微基准测试框架)进行性能测试和优化_java热点函数-CSDN博客 参考以上性能测试工具的使用。 Java开发手册中有这样一条…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...
