十六、【机器学习】【监督学习】- 支持向量回归 (SVR)
系列文章目录
第一章 【机器学习】初识机器学习
第二章 【机器学习】【监督学习】- 逻辑回归算法 (Logistic Regression)
第三章 【机器学习】【监督学习】- 支持向量机 (SVM)
第四章【机器学习】【监督学习】- K-近邻算法 (K-NN)
第五章【机器学习】【监督学习】- 决策树 (Decision Trees)
第六章【机器学习】【监督学习】- 梯度提升机 (Gradient Boosting Machine, GBM)
第七章 【机器学习】【监督学习】-神经网络 (Neural Networks)
第八章【机器学习】【监督学习】-卷积神经网络 (CNN)
第九章【机器学习】【监督学习】-循环神经网络 (RNN)
第十章【机器学习】【监督学习】-线性回归
第十一章【机器学习】【监督学习】-局部加权线性回归 (Locally Weighted Linear Regression, LWLR)
第十二章【机器学习】【监督学习】- 岭回归 (Ridge Regression)
十三、【机器学习】【监督学习】- Lasso回归 (Least Absolute Shrinkage and Selection Operator)
十四、【机器学习】【监督学习】- 弹性网回归 (Elastic Net Regression)
十五、【机器学习】【监督学习】- 神经网络回归
目录
系列文章目录
前言
一、基本定义
(一)、监督学习
(二)、监督学习的基本流程
(三)、监督学习分类算法(Classification)
二、 神经网络回归
(一)、定义
(二)、基本概念
(三)、训练过程
(四)、特点
(五)、适用场景
(六)、扩展
三、总结
前言
在先前的文章系列中,我们深入探讨了机器学习的基础框架和算法分类,为读者构建了关于这一领域的坚实理论基础。本章节我们将焦点转向监督学习领域中的一个核心算法—— 神经网络回归,旨在详尽解析其内在逻辑、应用实践及重要参数调整策略。
一、基本定义
(一)、监督学习
监督学习(Supervised Learning)是机器学习中的一种主要方法,其核心思想是通过已知的输入-输出对(即带有标签的数据集)来训练模型,从而使模型能够泛化到未见的新数据上,做出正确的预测或分类。在监督学习过程中,算法“学习”的依据是这些已标记的例子,目标是找到输入特征与预期输出之间的映射关系。
(二)、监督学习的基本流程
数据收集:获取包含输入特征和对应正确输出标签的训练数据集。
数据预处理:清洗数据,处理缺失值,特征选择与转换,标准化或归一化数据等,以便于模型学习。
模型选择:选择合适的算法,如决策树、支持向量机、神经网络等。
训练:使用训练数据集调整模型参数,最小化预测输出与实际标签之间的差距(损失函数)。
验证与调优:使用验证集评估模型性能,调整超参数以优化模型。
测试:最后使用独立的测试集评估模型的泛化能力,确保模型不仅在训练数据上表现良好,也能在未见过的新数据上做出准确预测。
(三)、监督学习分类算法(Classification)
定义:分类任务的目标是学习一个模型,该模型能够将输入数据分配到预定义的几个类别中的一个。这是一个监督学习问题,需要有一组已经标记好类别的训练数据,模型会根据这些数据学习如何区分不同类别。
例子:垃圾邮件检测(垃圾邮件 vs. 非垃圾邮件)、图像识别(猫 vs. 狗)。
二、 神经网络回归
(一)、定义
支持向量回归(Support Vector Regression, SVR)是支持向量机(Support Vector Machine, SVM)在回归分析中的应用。SVR是一种监督学习算法,用于预测连续值输出。它基于结构风险最小化原则,旨在找到一个函数,使得该函数与训练数据的偏差在一个预设的界限内尽可能小,同时保持模型的复杂度尽可能低。
(二)、基本概念
- 间隔 (Margin) 和容忍偏差 (Epsilon, ε):SVR试图找到一个间隔,即一个界限区域,在这个区域内的任何数据点都被认为是预测正确的,即使它们与真实值有轻微偏差。这个界限通常由一个参数ε来控制,ε定义了模型预测值与实际值之间的最大允许偏差。
- 支持向量 (Support Vectors):训练数据中那些落在间隔边界上的点被称为支持向量。它们是唯一决定SVR模型形状的点,而远离间隔边界的数据点对模型的影响较小。
- 核函数 (Kernel Function):SVR可以使用不同的核函数,如线性、多项式、径向基函数(RBF)等,来将数据映射到更高维空间,以便在非线性数据上进行回归分析。
(三)、训练过程
SVR的训练过程涉及解决一个优化问题,目的是找到一个最佳的超平面(对于线性SVR)或决策边界(对于非线性SVR),该边界能够以最小的误差预测目标值。以下是一个详细的训练过程概述:
-
数据准备:
- 数据预处理:清洗数据,处理缺失值,进行特征缩放(如标准化或归一化),编码分类特征。
- 数据划分:将数据集分为训练集和测试集(有时还包括验证集)。
-
模型初始化:
- 设定参数:选择损失函数(如ε-insensitive loss),设定惩罚参数C,选择核函数(如线性、多项式、RBF等),并设定核函数的参数(如γ)。
- 初始化权重向量w和偏置b(对于线性SVR),虽然它们在求解过程中会被更新。
-
构建优化问题:
- SVR的目标是找到一个函数f(x),使得对于所有训练样本(x_i, y_i),|f(x_i) - y_i| <= ε 或者 |f(x_i) - y_i| <= ε + ξ_i,其中ξ_i是松弛变量,用于允许一定的偏差,而ε是预先设定的误差容忍度。
- 目标是最小化损失函数(通常是对松弛变量的惩罚)和模型复杂度的加权和,以防止过拟合。
-
求解优化问题:
- 使用拉格朗日乘数法将原始问题转化为对偶问题,这通常涉及到二次规划问题的求解。
- 应用二次规划求解器来找到最优的拉格朗日乘数α_i,这一步可能涉及到内点法、梯度下降或其他优化算法。
-
确定支持向量:
- 只有那些与间隔边界相接触的点(即非零拉格朗日乘数α_i对应的点)被认为是支持向量。
- 支持向量决定了超平面的位置和方向。
-
构建回归函数:
- 根据求解的拉格朗日乘数α_i和相应的支持向量,构建回归函数f(x) = ∑[α_i * y_i * K(x, x_i)] + b,其中K(x, x_i)是核函数。
-
模型评估与调整:
- 在测试集上评估模型的性能,使用如均方误差(MSE)、平均绝对误差(MAE)等指标。
- 根据测试结果调整参数,如C、ε、核函数参数,可能通过网格搜索或随机搜索等超参数优化方法。
-
模型部署:
- 最终确定模型后,可以将其部署到生产环境,用于预测未知数据。
(四)、特点
- 鲁棒性:SVR对异常值不敏感,因为只有落在间隔边界外的数据点才会影响优化目标。
- 非线性处理能力:通过使用非线性核函数,SVR能够处理非常复杂的非线性关系。
- 参数调整:SVR具有多个参数,如C、ε和核函数参数,这为模型的调整提供了灵活性。
- 稀疏解决方案:SVR通常只需要支持向量来构建模型,这使得模型更加简洁高效。
- 避免过拟合:通过控制模型复杂度和惩罚参数C,SVR能够在训练数据拟合和泛化能力之间找到平衡。
- 计算复杂度:尽管SVR在处理小到中等规模数据集时表现良好,但在大规模数据集上,训练过程可能会变得非常计算密集。
SVR在处理具有复杂非线性模式的数据集时尤其有用,尤其是在数据量适中、特征维度较高的情况下。它广泛应用于金融、生物信息学、工程和其他领域,用于预测和建模。
(五)、适用场景
SVR适用于多种场景,特别是当数据具有非线性特性时,包括但不限于:
- 经济预测:如预测股市指数、汇率变动。
- 能源预测:预测电力需求、石油价格。
- 生物医学应用:如预测药物反应、蛋白质结构。
- 环境科学:预测天气变化、污染物浓度。
- 工程技术:如预测设备故障时间、材料强度。
(六)、扩展
除了基本的SVR,还有几种变种和扩展,包括:
- ε-SVR:最常见的SVR形式,使用ε-insensitive loss函数。
- ν-SVR:通过参数ν直接控制支持向量的数量和容许的误差率。
- 线性SVR:使用线性核函数,适用于大规模数据集。
- 多输出SVR:可以同时预测多个连续输出变量。
三、总结
SVR 作为一种成熟的机器学习技术,不仅在现有领域发挥重要作用,而且随着技术进步和需求变化,其应用前景将更加广阔。未来,SVR 将在算法优化、数据处理能力和跨领域应用方面取得显著进展,成为解决复杂预测问题的关键工具。

相关文章:

十六、【机器学习】【监督学习】- 支持向量回归 (SVR)
系列文章目录 第一章 【机器学习】初识机器学习 第二章 【机器学习】【监督学习】- 逻辑回归算法 (Logistic Regression) 第三章 【机器学习】【监督学习】- 支持向量机 (SVM) 第四章【机器学习】【监督学习】- K-近邻算法 (K-NN) 第五章【机器学习】【监督学习】- 决策树…...

基于FPGA的多路选择器
目录 一、组合逻辑 二、多路选择器简介: 三、实战演练 摘要:本实验设计并实现了一个简单的多路选择器,文章后附工程代码 一、组合逻辑 组合逻辑是VerilogHDL设计中的一个重要组成部分。从电路本质上讲,组合逻辑电路的特点是输…...
)
面经学习(杭州实在智能实习)
个人评价 秃狼觉得本次的面试是有史以来难度最大的,问了很多陌生的八股文,项目问的比较少,估计是项目本来就没有什么亮点,也是第一次被面试官说菜的面试。不过在后续的学习上还是收获颇丰的。 1.说说你在实习中遇到的难点吧&…...

mysql、oracle、db2数据库连接参数
mysql、oracle、db2数据库连接参数 参数/数据库driverurlMysqlcom.mysql.jdbc.Driver 或 com.mysql.cj.jdbc.Driverjdbc:mysql://localhost:3306/数据库名Oracleoracle.jdbc.driver.OracleDriverjdbc:oracle:thin:localhost:1521:orcl 注:orcl为数据库SIDDB2com.ib…...

redis缓存击穿和缓存穿透的封装、缓存更新的CacheAside方案、数据预热
redis缓存击穿和缓存穿透的封装 一、首先是互斥锁二、封装为工具类三、调用四、数据预热五、缓存更新的CacheAside方案 (来源黑马redis) 一、首先是互斥锁 //拿到锁private boolean tryLock(String key) {Boolean flag stringRedisTemplate.opsForValue…...
几何 5 多边形)
ArcGIS Pro SDK (九)几何 5 多边形
ArcGIS Pro SDK (九)几何 5 多边形 文章目录 ArcGIS Pro SDK (九)几何 5 多边形1 构造多边形 - 从映射点的枚举2 构造多边形 - 从包络3 获取多边形的点4 获取多边形的各个部分5 枚举多边形的各个部分6 获取多边形的线段7 构建圆环…...

Docker 镜像使用和安装
1、简介 Docker是一个开源的应用容器引擎;是一个轻量级容器技术; Docker支持将软件编译成一个镜像;然后在镜像中各种软件做好配置,将镜像发布出去,其他使用者可以直接使用这个镜像; 运行中的这个镜像…...

JAVA:Filer过滤器+案例:请求IP访问限制和请求返回值修改
JAVA:Filer过滤器 介绍 Java中的Filter也被称为过滤器,它是Servlet技术的一部分,用于在web服务器上拦截请求和响应,以检查或转换其内容。 Filter的urlPatterns可以过滤特定地址http的请求,也可以利用Filter对访问请求…...

FastAPI -- 第三弹(自定义响应、中间件、代理、WebSockets)
路径操作的高级配置 OpenAPI 的 operationId from fastapi import FastAPIapp FastAPI()# 通过 operation_id 参数设置 app.get("/items/", operation_id"some_specific_id_you_define") async def read_items():return [{"item_id": "F…...

网安小贴士(16)网络安全体系
前言 网络安全体系是一个综合性的系统,旨在保护网络系统中的硬件、软件和数据免受未经授权的访问、泄露、破坏或篡改。这个体系涉及多个方面,包括网络安全策略、安全技术和安全管理等。 一、网络安全体系概述 网络安全体系通常包括以下几个关键组成部分…...

UCOSIII 中断管理接口剖析
引言 在实时操作系统中,中断处理是一个非常重要的环节。理解和掌握中断处理流程对提高系统实时性和稳定性至关重要。本文将详细解析uCOS-III内核中的中断管理接口,包括 OSIntEnter() 和 OSIntExit() 函数的流程,并结合流程图对各个步骤进行说…...

windows 11 PC查询连接过的wlan密码
1:管理员打开cmd 2:输入netsh wlan show profiles 3:netsh wlan show profiles Shw2024-5G keyclear 密码关键内容:12345678...

npm install 出现canvas错误
npm install canvas2.8.0 --ignore-scripts只要是:npm ERR! Failed at the XXXX.X.X install script 这种错误 都可以:npm install XXXX.X.X --ignore-scripts进行更改 https://blog.csdn.net/YXWik/article/details/119039561...

Python爬虫入门篇学习记录
免责声明 本文的爬虫知识仅用于合法和合理的数据收集,使用者需遵守相关法律法规及目标网站的爬取规则,尊重数据隐私,合理设置访问频率,不得用于非法目的或侵犯他人权益。因使用网络爬虫产生的任何法律纠纷或损失,由使用…...

怎样对 PostgreSQL 中的慢查询进行分析和优化?
🍅关注博主🎗️ 带你畅游技术世界,不错过每一次成长机会!📚领书:PostgreSQL 入门到精通.pdf 文章目录 怎样对 PostgreSQL 中的慢查询进行分析和优化?一、理解慢查询的危害二、找出慢查询&#x…...
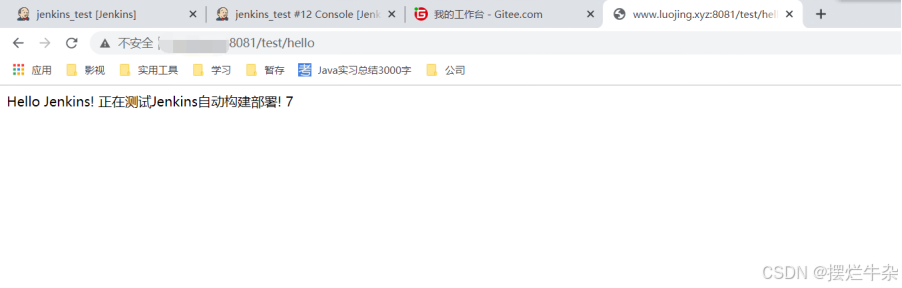
Springboot项目远程部署gitee仓库(docker+Jenkins+maven+git)
创建一个Springboot项目,勾选web将该项目创建git本地仓库,再创建远程仓库推送上去 创建TestController RestController RequestMapping("/test") public class TestController { GetMapping("/hello") public String sayHelloJe…...
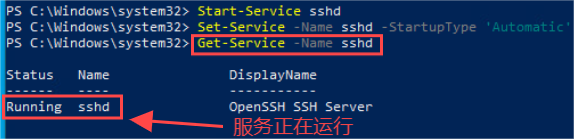
Chromium CI/CD 之Jenkins实用指南2024- Windows节点开启SSH服务(七)
1.引言 在现代软件开发和持续集成的过程中,自动化部署和远程管理是不可或缺的关键环节。SSH(Secure Shell)协议以其强大的安全性和灵活性,成为连接和管理远程服务器的首选工具。对于使用Windows虚拟机作为Jenkins从节点的开发者而…...
)
阿里大数据面试题集锦及参考答案(3万字长文:持续更新)
目录 MapReduce Shuffle为什么要将数据写入环形缓冲区 MapReduce Shuffle为什么容易发生数据倾斜 Hadoop HA当一个Namenode挂掉,会有数据丢失吗 数据倾斜发生的位置 Combiner了解吗? 什么情况下不能用Combiner? Sum、Count、Count(distinct)哪些能用、哪些不能用Comb…...
springboot 配置 spring data redis
1、在pom.xml引入父依赖spring-boot-starter-parent,其中2.7.18是最后一版支持java8的spring <parent><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-parent</artifactId><version>2.7.18</…...

Numpy基础用法
Numpy基础用法 numpy.all()num.sun() numpy.all() numpy 中的 all() 函数用于测试 NumPy 数组中所有元素是否都满足指定条件。它接受一个 NumPy 数组作为输入,并返回一个布尔值,指示数组中所有元素是否都满足条件。让我们通过具体的代码示例来深入探讨 n…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

并发编程 - go版
1.并发编程基础概念 进程和线程 A. 进程是程序在操作系统中的一次执行过程,系统进行资源分配和调度的一个独立单位。B. 线程是进程的一个执行实体,是CPU调度和分派的基本单位,它是比进程更小的能独立运行的基本单位。C.一个进程可以创建和撤销多个线程;同一个进程中…...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...

【从零开始学习JVM | 第四篇】类加载器和双亲委派机制(高频面试题)
前言: 双亲委派机制对于面试这块来说非常重要,在实际开发中也是经常遇见需要打破双亲委派的需求,今天我们一起来探索一下什么是双亲委派机制,在此之前我们先介绍一下类的加载器。 目录 编辑 前言: 类加载器 1. …...

WPF八大法则:告别模态窗口卡顿
⚙️ 核心问题:阻塞式模态窗口的缺陷 原始代码中ShowDialog()会阻塞UI线程,导致后续逻辑无法执行: var result modalWindow.ShowDialog(); // 线程阻塞 ProcessResult(result); // 必须等待窗口关闭根本问题:…...
)
华为OD最新机试真题-数组组成的最小数字-OD统一考试(B卷)
题目描述 给定一个整型数组,请从该数组中选择3个元素 组成最小数字并输出 (如果数组长度小于3,则选择数组中所有元素来组成最小数字)。 输入描述 行用半角逗号分割的字符串记录的整型数组,0<数组长度<= 100,0<整数的取值范围<= 10000。 输出描述 由3个元素组成…...
