Qt QProcess管道命令带“|”多命令执行获取stdout输出问题总结
问题描述:
在Qt中,使用system和QProcess执行命令,system执行的命令,我们通常不需要获取stdout的输出结果,所以只需要得到返回结果,知道成功失败即可。
而用到QProcess,多半是要获取输出的返回信息。
这里的返回信息只要是标准输出的即可,当然了,也可以是别的channel,只不过俺未曾见过。
一般情况下,执行命令可以很简单的如下方式:
QProcess process1;QString cmd = "free -h | grep 'Mem' ";process1.start(cmd);process1.waitForFinished();QString result = process1.readAll();qDebug()<<"result===="<<result;// if ( process1.exitCode() ) 省略,如果你有用的话,可以加上。执行单个命令,管道命令,都是可以的,但是,得区分命令的类型。如果你碰上了这样子无法执行,得到的结果是空,那么怎么办?
解决办法:
上面的例子或许不够生动,再举个栗子,功能都是获取系统内存大小:
相关文章:

Qt QProcess管道命令带“|”多命令执行获取stdout输出问题总结
问题描述: 在Qt中,使用system和QProcess执行命令,system执行的命令,我们通常不需要获取stdout的输出结果,所以只需要得到返回结果,知道成功失败即可。 而用到QProcess,多半是要获取输出的返回信息。 这里的返回信息只要是标准输出的即可,当然了,也可以是别的channe…...
【JavaEE进阶篇2】spring基于注解开发1
在上一篇文章当中,我们提到了怎样使用spring来创建一个bean对象。下面,我们继续来研究一下,更加优胜的开发方式:基于注解开发【JavaEE进阶篇1】认识Spring、认识IoC、使用spring创建对象_革凡成圣211的博客-CSDN博客springIoc、使…...

统一登录验证统一返回格式统一异常处理的实现
统一登录验证&统一返回格式&统一异常处理的实现 一、用户登录权限效验1.1 最初的用户登录验证1.2 Spring AOP 用户统一登录验证的问题1.3 Spring 拦截器1.3.1 准备工作1.3.2 自定义拦截器1.3.3 将自定义拦截器加入到系统配置1.4 拦截器实现原理1.4.1 实现原理源码分析1…...

【建议收藏】华为OD面试,什么场景下会使用到kafka,消息消费中需要注意哪些问题,kafka的幂等性,联合索引等问题
文章目录 华为 OD 面试流程一、什么场景下会使用到 kafka二、消息消费中需要注意哪些问题三、怎么处理重复消费四、kafka 的幂等性怎么处理的五、kafka 会怎么处理消费者消费失败的问题六、数据库设计中,你会如何去设计一张表七、联合索引有什么原则华为 OD 面试流程 机试:三…...
【MySQL】MySQL的优化(二)
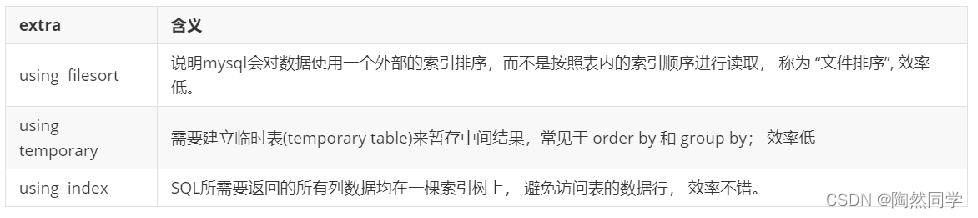
目录 explain分析执行计划 Explain分析执行计划-Explain 之 id Explain分析执行计划-Explain 之 select_type Explain分析执行计划-Explain 之 type Explain分析执行计划-其他指标字段 explain分析执行计划 通过以上步骤查询到效率低的 SQL 语句后,可以通过 …...
QT VTK开发 (一、下载编译)
Vtk,(visualization toolkit)是一个开源的免费软件系统,主要用于三维计算机图形学、图像处理和可视化。Vtk是在面向对象原理的基础上设计和实现的,它的内核是用C构建的,包含有大约250,000行代码,…...

C/C++每日一练(20230314)
目录 1. 移动数组中的元素 2. 搜索二维矩阵 3. 三角形最小路径和 🌟 每日一练刷题专栏 🌟 Golang 每日一练 专栏 C/C 每日一练 专栏 Python 每日一练 专栏 Java 每日一练 专栏 1. 移动数组中的元素 将一维数组中的元素循环左移 k 个位置 输入…...

裸辞3个月,面试了25家公司,终于找到心仪的工作了
上半年裁员,下半年裸辞,有不少人高呼裸辞后躺平真的好快乐!但也有很多人,裸辞后的生活五味杂陈。 面试25次终于找到心仪工作 因为工作压力大、领导PUA等各种原因,今年2月下旬我从一家互联网小厂裸辞,没…...
【Linux学习】进程间通信——system V(共享内存 | 消息队列 | 信号量)
🐱作者:一只大喵咪1201 🐱专栏:《Linux学习》 🔥格言:你只管努力,剩下的交给时间! 进程间通信——共享内存 | 消息队列 | 信号量🏀共享内存⚽系统调用shmgetkey值⚽系统…...
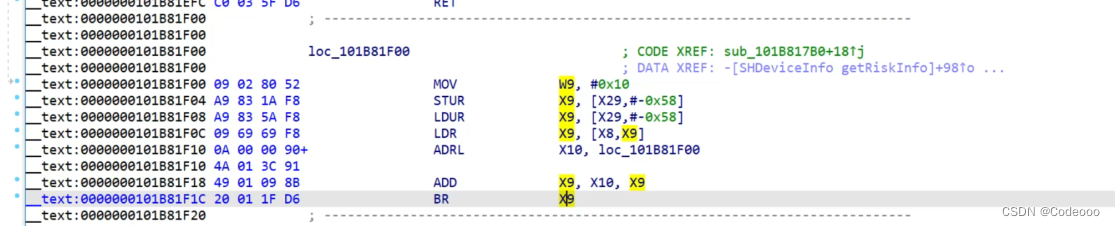
解决 IDA 防F5转伪C笔记
某app砸壳后放到IDA,根据堆栈查到该位置如下; G调到,0x1b81bcc 看下: BR 调到后面 x8 x9地址,汇编指令; 找到x9的地址,然后减去基地址也就是首地址,得到便宜地址; hook x9: var moduleAddr = Module.findBaseAddress("XX"); var line = moduleAddr.add...

【面试题】你需要知道的webpack高频面试题
大厂面试题分享 面试题库前后端面试题库 (面试必备) 推荐:★★★★★地址:前端面试题库谈谈你对webpack的看法webpack是一个模块打包工具,可以使用它管理项目中的模块依赖,并编译输出模块所需的静态文件。它…...

【YOLOv8/YOLOv7/YOLOv5/YOLOv4/Faster-rcnn系列算法改进NO.60】损失函数改进为wiou
前言作为当前先进的深度学习目标检测算法YOLOv8,已经集合了大量的trick,但是还是有提高和改进的空间,针对具体应用场景下的检测难点,可以不同的改进方法。此后的系列文章,将重点对YOLOv8的如何改进进行详细的介绍&…...
attack解析(详细))
2023年中职网络安全竞赛——数字取证调查(新版)attack解析(详细)
数字取证调查 任务环境说明: 服务器场景:FTPServer20221010(关闭链接)服务器场景操作系统:未知FTP用户名:attack817密码:attack817分析attack.pcapng数据包文件,通过分析数据包attack.pcapng找出恶意用户第一次访问HTTP服务的数据包是第几号,将该号数作为Flag值提交;…...

Cadence Allegro 导出Net Single Pin and No Pin报告详解
⏪《上一篇》 🏡《上级目录》 ⏩《下一篇》 目录 1,概述2,Net Single Pin and No Pin作用3,Net Single Pin and No Pin示例4,Net Single Pin and No Pin导出方法4.1,方法14.2,方法2B站关注“硬小二”浏览更多演示视频...
蓝桥冲刺31天之317
在这个时代,我们总是在比较,觉得自己不够好 其实不必羡慕别人的闪光点 每个人都是属于自己的限量版 做你喜欢并且擅长的事,做到极致 自然会找到自己独一无二的价值 鸟不跟鱼比游泳,鱼不跟鸟比飞翔 你我各有所长 A:组队…...
站上风口,文心一言任重道远
目录正式发布时机选择逻辑推理AI绘画用户选择总结自从OpenAI公司的chatGPT发布以来,吸引了全球目光,同时也引起了我们的羡慕,希望有国产的聊天机器人,盼星星盼月亮,终于等来了百度文心一言的发布。 正式发布 3月16日…...

Qt音视频开发24-视频显示QOpenGLWidget方式(占用GPU)
一、前言 采用painter的方式绘制解码后的图片,方式简单易懂,巨大缺点就是占CPU,一个两个通道还好,基本上CPU很低,但是到了16个64个通道的时候,会发现CPU也是很吃紧(当然强劲的电脑配置另当别论…...

百度发布文心一言,我想说几句
大家好,我是记得诚。 今天下午百度公司正式发布了文心一言,算是国内第一个交卷的互联网公司。 在ChatGPT和GPT-4的双重夹击下,可想而知百度的压力。 ChatGPT发布的时候,热度非常的高,大家对其都非常的感兴趣。 我是…...

简单了解JSP
JSP概念与原理概念: Java Server Pages,Java服务端页面一种动态的网页技术,其中既可以定义 HTML、JS、CSS等静态内容,还可以定义Java代码的动态内容JSP HTML Java, 用于简化开发JSP的本质上就是一个ServletJSP 在被访问时,由JSP容…...
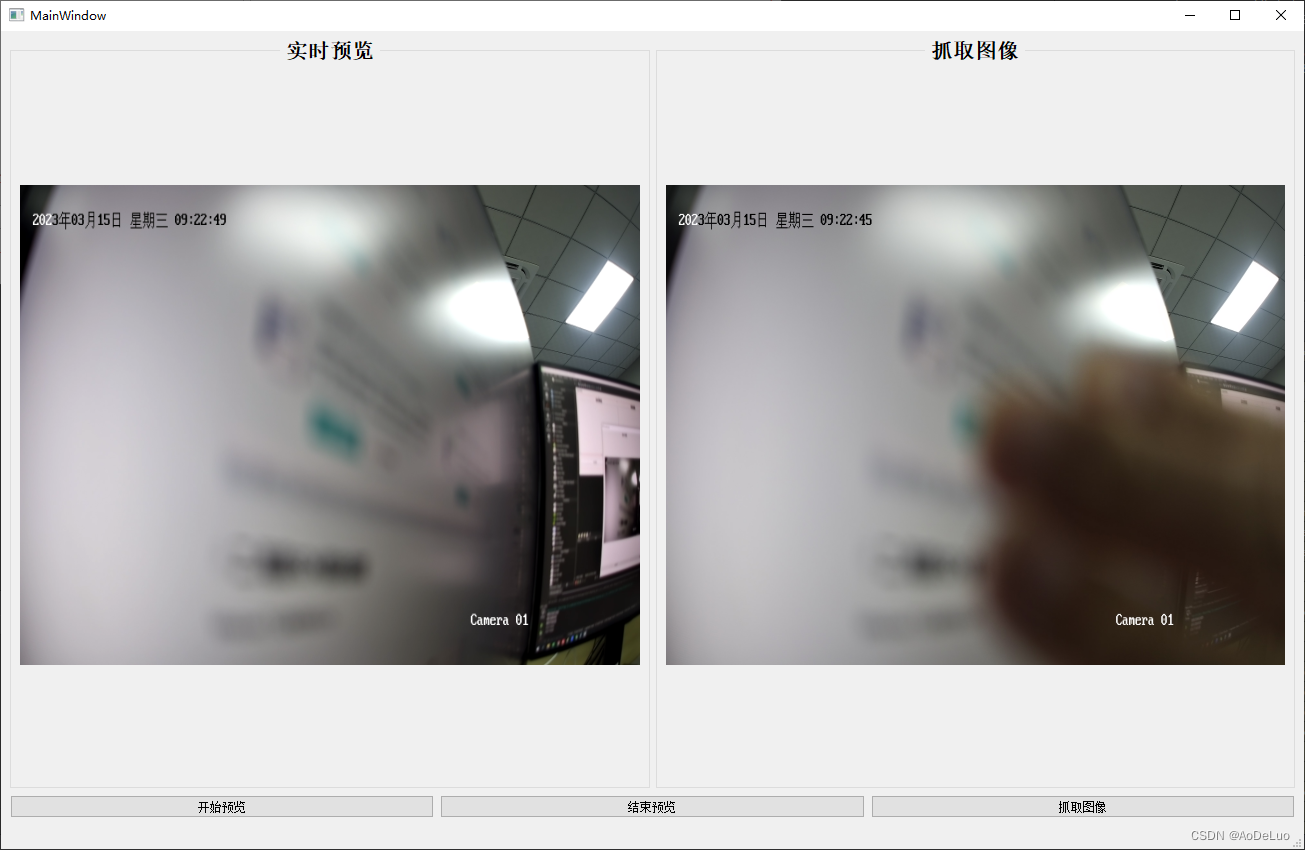
Qt(c++)调用海康威视监控摄像头
文章目录一.海康威视监控摄像头开发SDK介绍二.海康SDK模块说明三.Qt项目中海康威视SDK配置四.实时预览摄像头图像程序一.海康威视监控摄像头开发SDK介绍 设备网络SDK是基于设备私有网络通信协议开发的,为嵌入式网络硬盘录像机、NVR、网络摄像机、网络球机、视频服务…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...
基础)
6个月Python学习计划 Day 16 - 面向对象编程(OOP)基础
第三周 Day 3 🎯 今日目标 理解类(class)和对象(object)的关系学会定义类的属性、方法和构造函数(init)掌握对象的创建与使用初识封装、继承和多态的基本概念(预告) &a…...

6️⃣Go 语言中的哈希、加密与序列化:通往区块链世界的钥匙
Go 语言中的哈希、加密与序列化:通往区块链世界的钥匙 一、前言:离区块链还有多远? 区块链听起来可能遥不可及,似乎是只有密码学专家和资深工程师才能涉足的领域。但事实上,构建一个区块链的核心并不复杂,尤其当你已经掌握了一门系统编程语言,比如 Go。 要真正理解区…...

【免费数据】2005-2019年我国272个地级市的旅游竞争力多指标数据(33个指标)
旅游业是一个城市的重要产业构成。旅游竞争力是一个城市竞争力的重要构成部分。一个城市的旅游竞争力反映了其在旅游市场竞争中的比较优势。 今日我们分享的是2005-2019年我国272个地级市的旅游竞争力多指标数据!该数据集源自2025年4月发表于《地理学报》的论文成果…...

内窥镜检查中基于提示的息肉分割|文献速递-深度学习医疗AI最新文献
Title 题目 Prompt-based polyp segmentation during endoscopy 内窥镜检查中基于提示的息肉分割 01 文献速递介绍 以下是对这段英文内容的中文翻译: ### 胃肠道癌症的发病率呈上升趋势,且有年轻化倾向(Bray等人,2018&#x…...

用鸿蒙HarmonyOS5实现国际象棋小游戏的过程
下面是一个基于鸿蒙OS (HarmonyOS) 的国际象棋小游戏的完整实现代码,使用Java语言和鸿蒙的Ability框架。 1. 项目结构 /src/main/java/com/example/chess/├── MainAbilitySlice.java // 主界面逻辑├── ChessView.java // 游戏视图和逻辑├── …...
