数据结构-C语言-排序(3)
代码位置:test-c-2024: 对C语言习题代码的练习 (gitee.com)
一、前言:
1.1-排序定义:
排序就是将一组杂乱无章的数据按照一定的规律(升序或降序)组织起来。(注:我们这里的排序采用的都为升序)
1.2-排序分类:
常见的排序算法:
-
插入排序
a. 直接插入排序
b. 希尔排序 - 选择排序
a. 选择排序
b. 堆排序 - 交换排序
a. 冒泡排序
b. 快速排序 - 归并排序
a. 归并排序 - 非比较排序
a.计数排序
b.基数排序
1.3-算法比较:

1.4-目的:
今天,我们这里要实现的是快速排序。
1.5-快速排序定义:
通过一趟排序将待排记录分割成独立的两部分,其中一部分记录的关键字均比另一部分的关键字小,然后分别对这两部分记录继续进行排序,以达到整个序列有序。
二、快速排序-key的选择:
2.1-直接在left和right中选择:
这种选择方法具有局限性如果排序的序列已经为升序的情况下,根据快速排序的定义,我们可知,快速排序的话,会确定一个值的位置也就是key,这个值的作用就是把数据分割成独立的两部分,一部分是比他大,一部分是比他小,而如果是升序的情况下直接选择left,选出的left的值是最小的,也就是说右面的部分是N-1个数据,而如果是用递归的方式实现的快排,那么就需要递归N次,也就是建立N个栈才能实现最终排序的操作,如果数据量大就很有可能出现栈溢出的情况。
该情况下递归的图片如图所示:

2.2-随机选择key:
随机选择key,也就是说,在数组下标范围内,随机生成一个下标,采用这个下标位置的数据值作为key这样的情况下,我们就大大降低了选出的key是最小值的情况。能有效地减少栈溢出的情况。
2.3-三数取中:
三数取中就是在left 、midi((right+left)/2) 、right三个下标位置上的数据之间选择出这三个数据中的中间数。这样就避免了key为最小值的情况。
2.4-代码:
void Swap(int* p, int* q) //交换函数
{int tem = *p;*p = *q;*q = tem;
}//直接选取法
int keyi = left;//随机选keyi
int randi = left + (rand() % (right - left));
Swap(&a[randi], &a[left]);
int keyi = left;//三数取中
int midi = GetMidNumi(a, left, right);
if (midi != left)Swap(&a[midi], &a[left]);
int keyi = left;int GetMidNumi(int* a, int left, int right) //三数取中法
{int mid = (left + right) / 2;if (a[left] > a[mid]){if (a[mid] > a[right]){return mid;}if (a[left] < a[right]){return left;}else{return right;}}if (a[left] < a[mid]){if (a[left] > a[right]){return left;}if (a[right] > a[mid]){return mid;}else{return right;}}
}三、快速排序-Hoare:
3.1-思路:
Hoare快速排序的思路就是:
如果key定义的是left,那么就首先从右边找小,找到以后再从左边出发找大,找完以后后将他们俩的数据调换,然后接着进行下一次先右后左找小再找大,直到left小于right为止。同理若定义key在right处那么就先左后右,处理方式与left类似。
这样排完一趟后,我们能将大于key的数分布在右边,小于key的数分布在左边,最后,我们只需要按照这个思路递归下去,就实现快速排序啦。
注意:在递归时,如果出现left>=right的情况下,我们就需要返回,否则就会死循环。
左边做key为什么相遇位置一定比key小?

3.2-过程图:

3.3-代码:
//Hoare
void QuickSort1(int* a, int left,int right) //快速排序---时间复杂度(O(N*logN))
{if (left >= right)return;int begin = left;int end = right;//直接选取法//int keyi = left;//随机选keyi//int randi = left + (rand() % (right - left));//Swap(&a[randi], &a[left]);//int keyi = left;//三数取中int midi = GetMidNumi(a, left, right);if(midi!=left)Swap(&a[midi], &a[left]);int keyi = left;while (left < right){//右边找小while (left<right&&a[right] >=a[keyi]){--right;}//左边找大while (left<right&&a[left] <= a[keyi]){++left;}Swap(&a[left], &a[right]);}Swap(&a[keyi], &a[left]);keyi = left;//递归---小区间优化--小区间直接使用插入排序if (end - begin+1 > 10){QuickSort1(a, begin, keyi - 1);QuickSort1(a, keyi + 1, end);}else{InsertSort(a + begin, end - begin + 1);}
}四、快速排序-挖坑法:
4.1-思路:
快速排序,挖坑法的思路就是:
先将第一个数据存放在临时变量k中,形成一个坑位,然后再数组的右边出发,向左寻找小于key的数,然后将这个数填在以前的坑位上,然后在该处重新生成坑位,接着在从左边向右寻找,找大于ker的数,然后将这个数填在生成的坑位上,然后在该处重新生成坑位,就这样一直循环实现上述操作,直到left与right相遇为止,此时,该坑位就应该填key。。
这样排完一趟后,我们能将大于key的数分布在右边,小于key的数分布在左边,最后,我们只需要按照这个思路递归下去,就实现快速排序啦。
注意:在递归时,如果出现left>=right的情况下,我们就需要返回,否则就会死循环。
4.2-过程图:

4.3-代码:
//挖坑法
void QuickSort2(int* a, int left, int right) //快速排序---时间复杂度(O(N*logN))
{if (left >= right)return;int begin = left;int end = right;//直接选取法//int keyi = left;//随机选keyi//int randi = left + (rand() % (right - left));//Swap(&a[randi], &a[left]);//int keyi = left;//三数取中int midi = GetMidNumi(a, left, right);if(midi!=left)Swap(&a[midi], &a[left]);int key = a[left];int hole = left;while (left < right){while (left < right &&a[right] >= key){--right;}a[hole] = a[right];hole = right;while (left < right&&a[left] <= key){++left;}a[hole] = a[left];hole = left;}a[hole] = key;//递归---小区间优化--小区间直接使用插入排序if (end - begin + 1 > 10){QuickSort2(a, begin, hole - 1);QuickSort2(a, hole + 1, end);}else{InsertSort(a + begin, end - begin + 1);}
}五、快速排序-前后指针法:
5.1-思路:
快速排序,前后指针法的思路就是:
首先,定义一个prev=left ; cur=left+1。这里我们实现的操作:
1.cur找到比key小的值,++prove, cur和prev位置的数调换,然后++cur。
2.cur找到比key大的值,++cur。
说明:
1.prev要么紧跟着cur(prev下一个位置就是cur)。
2.prev跟cur中间隔着一段比key大的值。
就这样,按上述思想进入循环知道,直到cur走到数组末端的下一个位置为止,接下来我们要实行的操作就是将keyi位置的值(key)与prev位置的值交换。这样排完一趟后,我们能将大于key的数分布在右边,小于key的数分布在左边,最后,我们只需要按照这个思路递归下去,就实现快速排序啦。
注意:在递归时,如果出现left>=right的情况下,我们就需要返回,否则就会死循环。
5.2-过程图:

5.3-代码:
//前后指针法
void QuickSort3(int* a, int left, int right) //快速排序---时间复杂度(O(N*logN))
{if (left>=right)return;int begin = left;int end = right;//直接选取法//int keyi = left;//随机选keyi//int randi = left + (rand() % (right - left));//Swap(&a[randi], &a[left]);//int keyi = left;//三数取中int midi = GetMidNumi(a, left, right);if (midi != left)Swap(&a[midi], &a[left]);int keyi = left;int prev= left;int cur = left + 1;while (cur<=right){if(a[cur]<a[keyi]&&++prev!=cur)Swap(&a[cur], &a[prev]);cur++;}Swap(&a[keyi], &a[prev]);keyi = prev;//递归---小区间优化--小区间直接使用插入排序if (end - begin + 1 > 10){QuickSort3(a, begin, keyi - 1);QuickSort3(a, keyi + 1, end);}else{InsertSort(a + begin, end - begin + 1);}}六、递归的问题与优化:
6.1-递归的问题:
1.效率问题(略有影响)。
2.深度太深时会栈溢出。
递归过程图:

6.2-小区间优化:
小区间优化的思想就是:
将递归的最后几层,也就是基本有序的小区间,采用直接插入排序的方法,不再采用递归的方式,这样能够减少递归时所开辟栈。
因为,递归栈的开辟相当于二叉树,而二叉树的最后一层相当于总数的一半,如果把最后一层省掉,也就是省去了递归所需开辟栈的大概50%的空间。
所以,我们可以通过小区间优化来减少栈的开辟,在不影响时间复杂度的情况下,也减小了深度太深时会栈溢出的问题。
6.3-小区间优化代码:
//递归---小区间优化--小区间直接使用插入排序
if (end - begin + 1 > 10)
{QuickSort3(a, begin, keyi - 1);QuickSort3(a, keyi + 1, end);
}
else
{InsertSort(a + begin, end - begin + 1);
}七、递归改非递归:
由上述可知,通过递归实现快排,具有一定的弊端,也就是栈溢出,所以这里我们可以采取将递归改成非递归的方式来实现快速排序
7.1-方式:
1.直接改成循环。
2.使用栈辅助改成循环。
通过上述代码可观察发现,递归改非递归的第一种方式,我们是实现不了的,所以我们这里需要借助栈来辅助将递归改成循环。
7.2-思路:
这里的思路就是将递归时的左右区间,存入栈中。然后在循环的过程中,我们只需将区间值出站即可。
注意:栈的原理是后进先出。
7.3-代码:
#include "Stack.h"
//递归改非递归
void QuickSortNonR(int* a, int left, int right) //快速排序---时间复杂度(O(N*logN))
{ST ps;STInit(&ps);STpush(&ps, right); //入栈STpush(&ps, left); //入栈while (!STEmpty(&ps)){int begin= STTop(&ps); //取栈顶元素STPop(&ps); //出栈int end = STTop(&ps); //取栈顶元素STPop(&ps); //出栈int midi = GetMidNumi(a, begin, end);if (midi != begin)Swap(&a[midi], &a[begin]);int keyi = begin;int prev = begin;int cur = begin + 1;while (cur <= end){if (a[cur] < a[keyi] && ++prev != cur)Swap(&a[cur], &a[prev]);cur++;}Swap(&a[keyi], &a[prev]);keyi = prev;if (keyi + 1 < end){STpush(&ps, end); //入栈STpush(&ps, keyi + 1); //入栈}if (keyi - 1 > begin){STpush(&ps, keyi - 1); //入栈STpush(&ps, begin); //入栈}}for (int i = 0; i <=right; i++){printf("%d ", a[i]);}printf("\n");STDestory(&ps);
}
7.4-栈的代码:
#pragma once#include <stdio.h>
#include <assert.h>
#include <stdlib.h>
#include <stdbool.h>typedef int STDataType;
typedef struct Stack
{STDataType* a;int top;int capacity;
}ST;void STInit(ST* ps); //初始化
void STDestory(ST* ps); //释放销毁void STpush(ST* ps, STDataType x); //入栈
void STPop(ST* ps); //出栈
int STSize(ST* ps); //栈中元素个数
bool STEmpty(ST* ps); //判断栈空
STDataType STTop(ST* ps); //栈顶元素#define _CRT_SECURE_NO_WARNINGS 1
#include "Stack.h"void STInit(ST* ps) //初始化
{assert(ps);ps->a = (STDataType*)malloc(sizeof(STDataType) * 4);if (ps->a == NULL){perror("malloc");return;}ps->capacity = 4;ps->top = 0; //top是栈顶元素的下一个位置//ps->top=-1 //top是栈顶元素位置
}void STDestory(ST* ps) //释放销毁
{assert(ps);ps->top = 0;ps->capacity = 0;free(ps->a);ps->a = NULL;
}void STpush(ST* ps, STDataType x) //入栈
{assert(ps);if (ps->top == ps->capacity){STDataType* tem = (STDataType*)realloc(ps->a, sizeof(STDataType) * ps->capacity * 2);if (tem == NULL){perror("realloc");return;}ps->a = tem;ps->capacity *= 2;}ps->a[ps->top] = x;ps->top++;
}void STPop(ST* ps) //出栈
{assert(ps);assert(!STEmpty(ps));ps->top--;
}int STSize(ST* ps) //栈中元素个数
{assert(ps);return ps->top;
}bool STEmpty(ST* ps) //判断栈空
{assert(ps);return ps->top == 0;
}STDataType STTop(ST* ps) //返回栈顶元素
{assert(ps);assert(!STEmpty(ps));return ps->a[ps->top - 1];
}
八、结语:
上述内容,即是我个人对数据结构排序中快速排序的个人见解以及自我实现。若有大佬发现哪里有问题可以私信或评论指教一下我这个小萌新。非常感谢各位友友们的点赞,关注,收藏与支持,我会更加努力的学习编程语言,还望各位多多关照,让我们一起进步吧!

相关文章:

数据结构-C语言-排序(3)
代码位置:test-c-2024: 对C语言习题代码的练习 (gitee.com) 一、前言: 1.1-排序定义: 排序就是将一组杂乱无章的数据按照一定的规律(升序或降序)组织起来。(注:我们这里的排序采用的都为升序) 1.2-排序分…...

【分布式事务】怎么解决分布式场景下数据一致性问题
分布式事务的由来 拿充值订单举个栗子吧,假设:原本订单模块和账户模块是放在一起的,现在需要做服务拆分,拆分成订单服务,账户余额服务。原本收到充值回调后,可以将修改订单状态和扣减余额放在一个mysql事务…...

C# 中的委托
委托的概念 在C#中,委托是一种引用类型,它表示对方法的引用,即委托就是一种用来指向一个方法的引用类型变量。委托的声明类似于方法签名,但是关键字是delegate。下面是一个委托的声明和使用的例子: // 声明一个委托 p…...

通过docker构建基于LNMP的WordPress项目
目录 1.准备nginx 2.准备mysql 3.准备php 4.构建各镜像 5.运行wordpress 1、项目环境: 1.1 (1)公司在实际的生产环境中,需要使用Docker 技术在一台主机上创建LNMP服务并运行Wordpress网站平台。然后对此服务进行相关的性能…...

2024新版IntelliJ IDEA修改包名 全网最简单最粗暴的方法
问题再现 我们在网上淘一些后端框架 又或者是开源的项目 如果要变成自己的 难免会去改包名 即把com.后面的内容改成自己自定义的 第一次我们直接用网络上的方法 shift F6 快捷键 可以修改包名 出现以下情况 进行修改 我们发现失败了 并没有像预计的一样直接把包名修…...

C#中处理Socket粘包
在C#中使用Socket进行网络通信时,粘包问题是常见的。粘包问题通常发生在TCP协议中,因为TCP是流式协议,数据可能会被分割成多个包发送,也可能多个小包会被合并成一个大包接收。 处理粘包问题的常见方法是使用消息分隔符或消息长度…...

7.19IO
思维导图 第一题:测试错误检查锁和递归锁是否会造成死锁状态 #include <stdio.h> #include <string.h> #include <stdlib.h> #include <unistd.h> #include <sys/types.h> #include <sys/stat.h> #include <fcntl.h> #i…...

【Vue】深入了解 Axios 在 Vue 中的使用:从基本操作到高级用法的全面指南
文章目录 一、Axios 简介与安装1. 什么是 Axios?2. 安装 Axios 二、在 Vue 组件中使用 Axios1. 发送 GET 请求2. 发送 POST 请求 三、Axios 拦截器1. 请求拦截器2. 响应拦截器 四、错误处理五、与 Vuex 结合使用1. 在 Vuex 中定义 actions2. 在组件中调用 Vuex acti…...
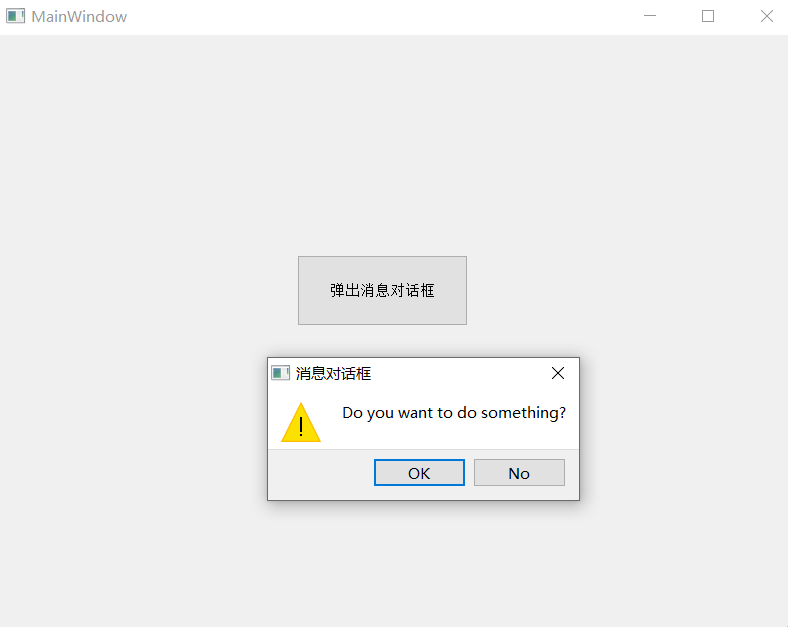
【Qt】窗口
文章目录 QMainWindow菜单栏工具栏状态栏浮动窗口对话框自定义对话框Qt内置对话框QMessageBox QMainWindow Qt中的主窗口以QMainWindow表示,其总体结构如下: 菜单栏 菜单栏MenuBar,可包含多个菜单Menu,每个菜单也可以包含多个菜…...

代码随想录训练营【贪心算法篇】
贪心 注:本文代码来自于代码随想录 贪心算法一般分为如下四步: 将问题分解为若干个子问题找出适合的贪心策略求解每一个子问题的最优解将局部最优解堆叠成全局最优解 这个四步其实过于理论化了,我们平时在做贪心类的题目 很难去按照这四步…...

Spark中的JOIN机制
Spark中的JOIN机制 1、Hash Join概述2、影响JOIN的因素3、Spark中的JOIN机制3.1、Shuffle Hash Join3.2、Broadcast Hash Join3.3、Sort Merge Join3.4、Cartesian Product Join3.5、Broadcast Nested Loop Join4、Spark中的JOIN策略5、Spark JOIN机制与策略总结5.1、Spark中的…...

WebRTC QOS方法十三.1(TimestampExtrapolator接收时间预估)
一、背景介绍 虽然我们可通过时间戳的差值和采样率计算出发送端视频帧的发送节奏,但是由于网络延迟、抖动、丢包,仅知道视频发送端的发送节奏是明显不够的。我们还需要评估出视频接收端的视频帧的接收节奏,然后进行适当平滑,保证…...

深入了解 GCC
GCC,全称 GNU Compiler Collection,是 GNU 项目的一部分,是一个功能强大且广泛使用的编译器套件。它支持多种编程语言,包括 C、C、Fortran、Java、Ada 和 Go。GCC 具有高度的可移植性,几乎可以在所有现代计算机体系结构…...

vscode 打开远程bug vscode Failed to parse remote port from server output
vscode 打开远程bug vscode Failed to parse remote port from server output 原因如图: 解决:...
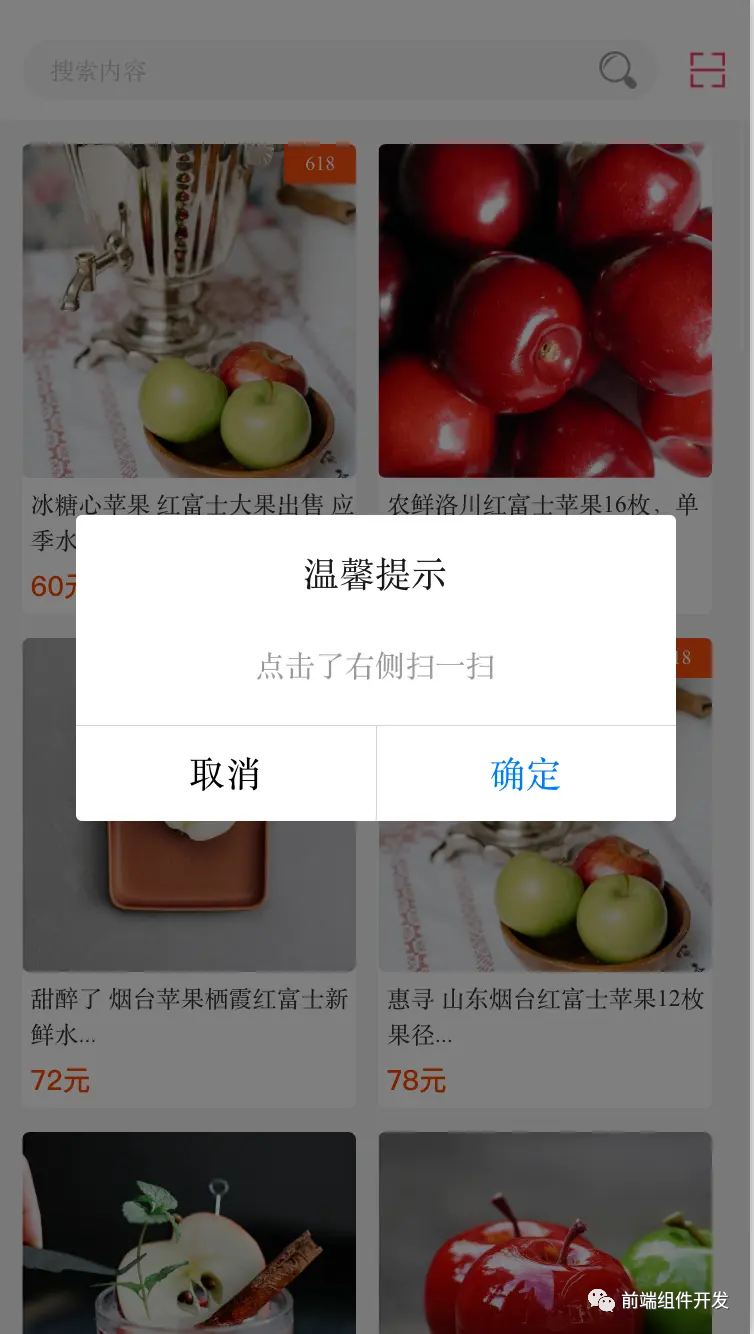
前端组件化技术实践:Vue自定义顶部导航栏组件的探索
摘要 随着前端技术的飞速发展,组件化开发已成为提高开发效率、降低维护成本的关键手段。本文将以Vue自定义顶部导航栏组件为例,深入探讨前端组件化开发的实践过程、优势以及面临的挑战,旨在为广大前端开发者提供有价值的参考和启示。 一、引…...

PyTorch Autograd内部实现
原文: 克補 爆炸篇 25s (youtube.com) 必应视频 (bing.com)https://www.bing.com/videos/riverview/relatedvideo?&qPyTorchautograd&qpvtPyTorchautograd&mid1B8AD76943EFADD541E01B8AD76943EFADD541E0&&FORMVRDGAR 前面只要有一个node的re…...

微信小程序 vant-weapp的 SwipeCell 滑动单元格 van-swipe-cell 滑动单元格不显示 和 样式问题 滑动后删除样式不显示
在微信小程序开发过程中 遇到个坑 此处引用 swipeCell 组件 刚开始是组件不显示 然后又遇到样式不生效 首先排除问题 是否在.json文件中引入了组件 {"usingComponents": {"van-swipe-cell": "vant/weapp/swipe-cell/index","van-cell-gro…...

3.4、matlab实现SGM/BM/SAD立体匹配算法计算视差图
1、matlab实现SGM/BM/SAD立体匹配算法计算视差图简介 SGM(Semi-Global Matching)、BM(Block Matching)和SAD(Sum of Absolute Differences)都是用于计算立体匹配(Stereo Matching)的…...

【瑞吉外卖 | day07】移动端菜品展示、购物车、下单
文章目录 瑞吉外卖 — day71. 导入用户地址簿相关功能代码1.1 需求分析1.2 数据模型1.3 代码开发 2. 菜品展示2.1 需求分析2.2 代码开发 3. 购物车3.1 需求分析3.2 数据模型3.3 代码开发 4. 下单4.1 需求分析4.2 数据模型4.3 代码开发 瑞吉外卖 — day7 移动端相关业务功能 —…...
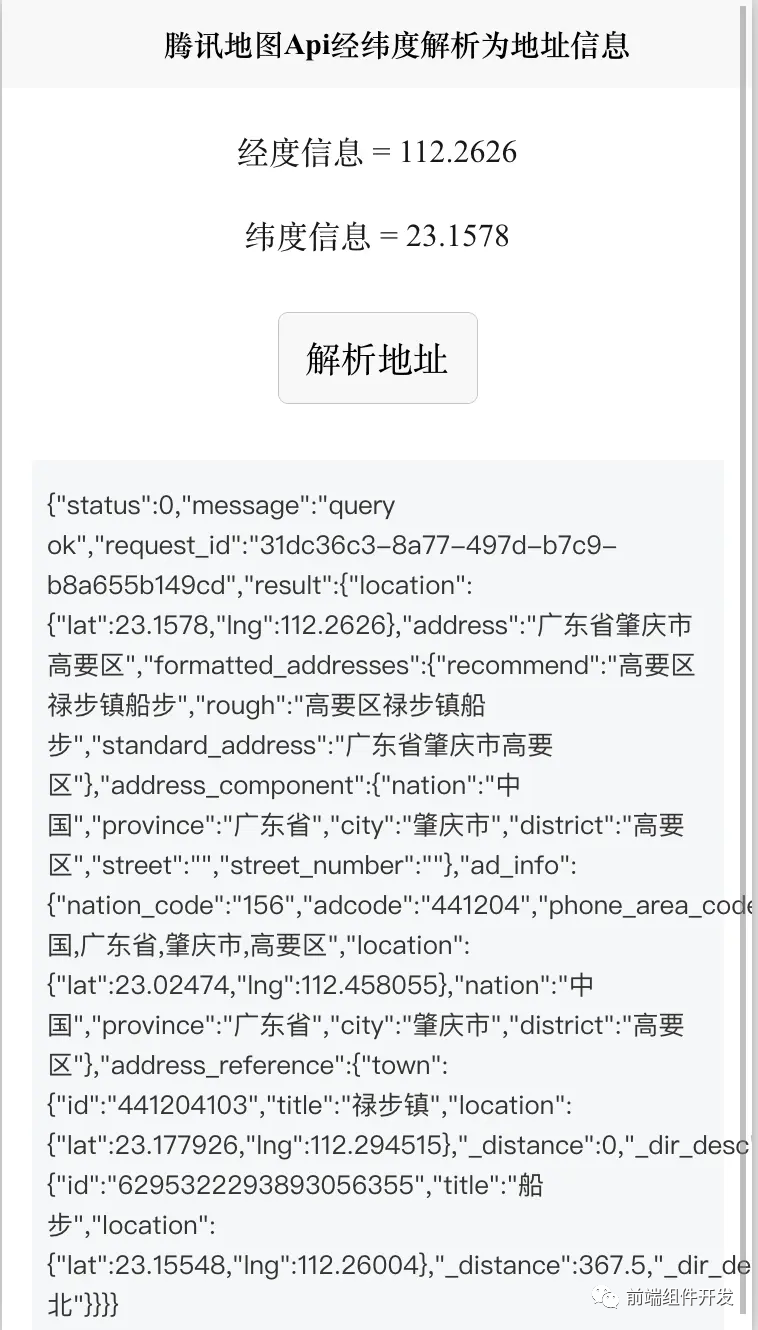
前端Vue项目中腾讯地图SDK集成:经纬度与地址信息解析的实践
在前端开发中,我们经常需要将经纬度信息转化为具体的地址信息,这对于定位、地图展示等功能至关重要。Vue作为现代前端框架的代表,其组件化开发的特性使得我们能够更高效地实现这一功能。本文将介绍如何在Vue项目中集成腾讯地图SDK,…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...
