JS设计模式（一）单例模式
注释很详细，直接上代码
本文建立在已有JS面向对象基础的前提下，若无，请移步以下博客先行了解
JS面向对象（一）类与对象写法
特点和用途：
- 全局访问点：通过单例模式可以在整个应用程序中访问同一个对象实例，而不要每次使用时都创建新的对象。
- 节省资源：特别是在需要频繁创建和销毁对象时，单例模式可以减少内存和资源占用。
- 数据共享：由于单例模式只有一个实例，可以确保数据在各个部分共享使用。
单例模式在开发中广泛应用，例如管理全局状态、配置信息、日志记录器等场景，确保整个应用程序中某个类只有一个实例是非常有用的
源码：
index.html
<!DOCTYPE html>
<html lang="en"><head><meta charset="UTF-8" /><meta name="viewport" content="width=device-width, initial-scale=1.0" /><title>Document</title></head><body></body><script>class LoginForm {constructor() {this.state = "hide";}show() {if (this.state === "show") {alert("已经显示");return;}this.state = "show";console.log("登录框显示成功");}hide() {if (this.state === "hide") {alert("已经隐藏");return;}this.state = "hide";console.log("登录框隐藏成功");}}LoginForm.getInstance = (function () {let instance; //因为是闭包，这个标识可以存储在函数内部，所以这里可以保证实例的唯一性return function () {if (!instance) {instance = new LoginForm();}return instance;};})();let obj1 = LoginForm.getInstance();obj1.show();let obj2 = LoginForm.getInstance();//两次获取的实例是同一个obj2.hide();console.log(obj1 === obj2);//这里演示一下闭包的应用//--------------------------------------------------/*function myTest() {let sum = 0;return function add(num) {sum += num;console.log(sum);};}let add = myTest();add(1);add(2);let add2 = myTest();add2(5);add2(6);*/</script>
</html>相关文章：
JS设计模式（一）单例模式
注释很详细，直接上代码 本文建立在已有JS面向对象基础的前提下，若无，请移步以下博客先行了解 JS面向对象（一）类与对象写法 特点和用途： 全局访问点：通过单例模式可以在整个应用程序中访问同一个…...
uniapp动态计算并设置元素高度
<template><view><scroll-view id"sv-box" :scroll-y"true" :style"{height:navHeightpx}"></scroll-view><view id"btn-box"><button>取消</button><button>确认</button><…...
直播架构如何设计核心节点和边缘节点
在直播架构中，核心节点和边缘节点的分工及主要服务是确保直播服务稳定、高效和可扩展的关键。以下是对这些节点的详细描述： 核心节点 核心节点通常位于数据中心，负责处理直播的主要逻辑和数据处理。其主要服务包括： 直播管理后…...
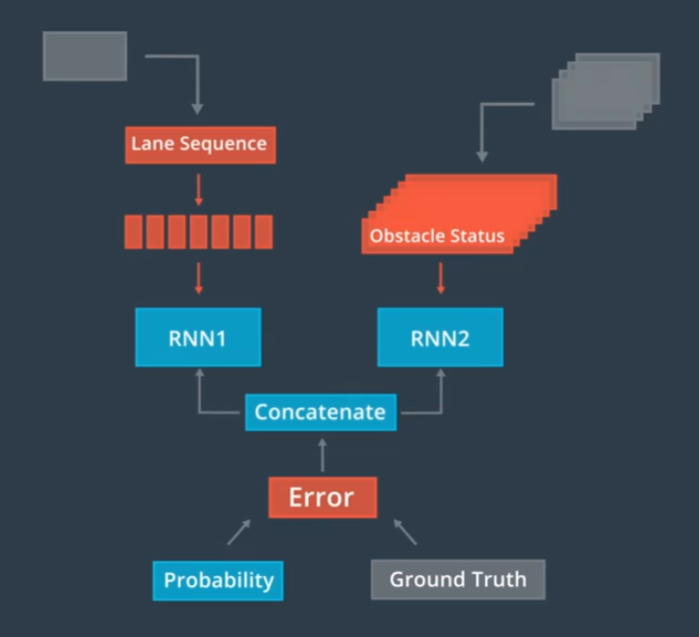
自动驾驶-预测概览
通过生成一条路径来预测一个物体的行为，在每一个时间段内，为每一辆汽车重新计算预测他们新生成的路径，这些预测路径为规划阶段做出决策提供了必要信息 预测路径有实时性的要求，预测模块能够学习新的行为。我们可以使用多源的数据…...
基于PSO算法优化PID参数的一些问题
目录 前言 Q1：惯性权重ω如何设置比较好？学习因子C1和C2如何设置？ Q2：迭代速度边界设定一定能够遍历（/覆盖）整个PID参数二维空间范围吗？还是说需要与迭代次数相关？迭代次数越高&a…...
什么是决策树？
1. 什么是决策树？ 决策树（Decision Tree）是一种常用的机器学习算法，用于解决分类和回归问题。它通过构建树结构来表示决策过程，分支节点表示特征选择，叶节点表示类别或回归值。 2. 决策树的组成部分 决策…...
ASP 快速参考
ASP 快速参考 概述 ASP（Active Server Pages）是一种由微软开发的服务器端脚本环境，用于动态网页设计和开发。它允许开发者创建和运行动态交互性网页，如访问数据库、发送电子邮件等。ASP页面通常以.asp为文件扩展名，并…...
(二)原生js案例之数码时钟计时
原生js实现的数字时间上下切换显示时间的效果，有参考相关设计，思路比较难，代码其实很简单 效果 代码实现 必要的样式 <style>* {padding: 0;margin: 0;}.content{/* text-align: center; */display: flex;align-items: center;justif…...
[CSS] 浮动布局的深入理解与应用
文章目录 浮动的简介元素浮动后的特点解决浮动产生的影响浮动后的影响解决浮动产生的影响 浮动相关属性实际应用示例示例1：图片与文字环绕示例2：多列布局示例3：响应式布局 总结 浮动布局是CSS中一种非常强大的布局方式，最初设计用…...
Linux云计算 |【第一阶段】ENGINEER-DAY2
主要内容： 磁盘空间管理fdisk、parted工具、开机自动挂载、文件系统、交换空间 KVM虚拟化 实操前骤： 1）添加一块硬盘（磁盘），需要关机才能进行操作，点击左下角【添加硬件】 2）选择2…...
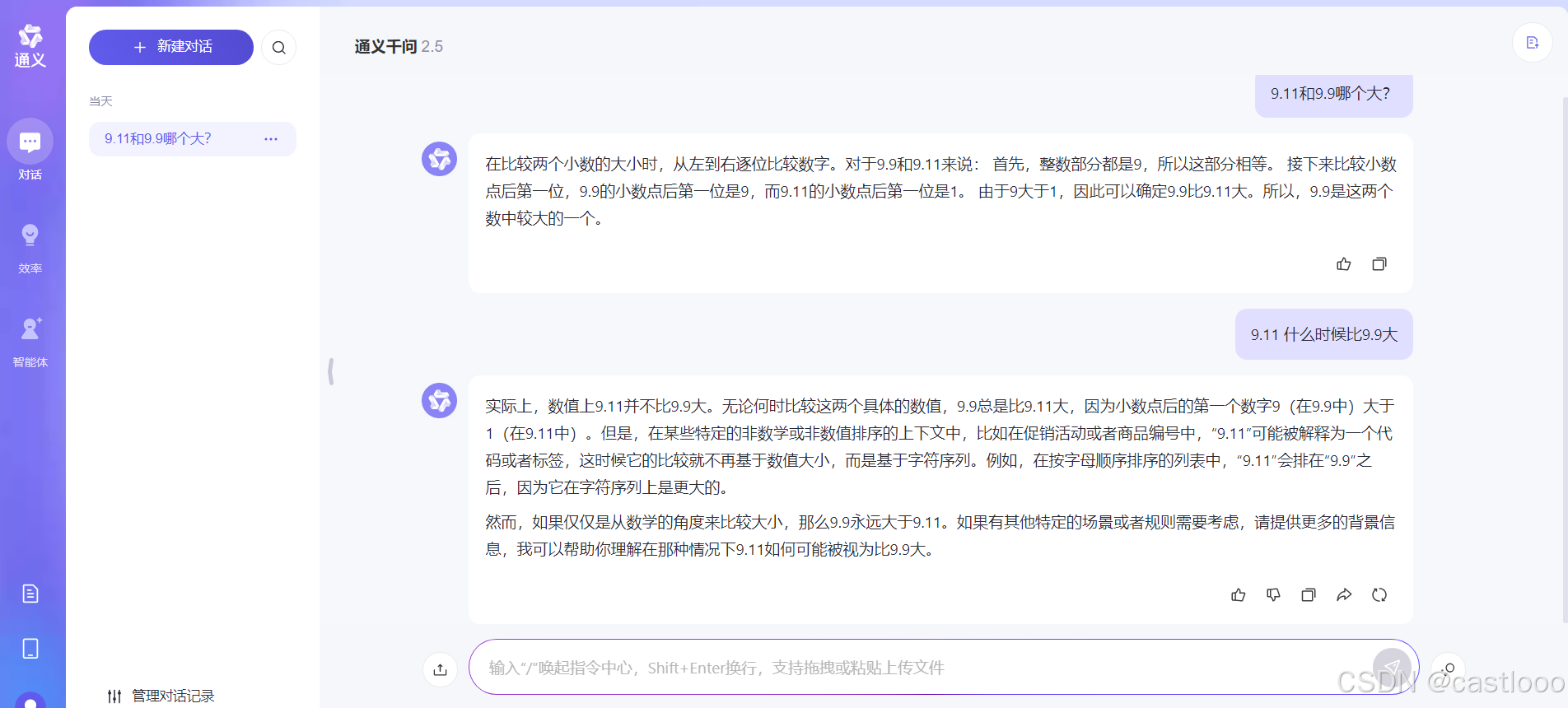
9.11和9.9哪个大？
没问题 文心一言 通义千问...
学懂C语言（十二）：C语言中的二进制原理及应用
目录 1. 二进制原理 1.1 什么是二进制？ 1.2 如何在C语言中表示二进制？ 2. 二进制的表示 2.1 二进制和其他进制的转换 2.2 C语言中的二进制表示 3. 二进制运算 3.1 位运算符 3.2 计算过程示例 4. 应用示例 4.1 使用位运算实现开关 5. 总结 C语…...
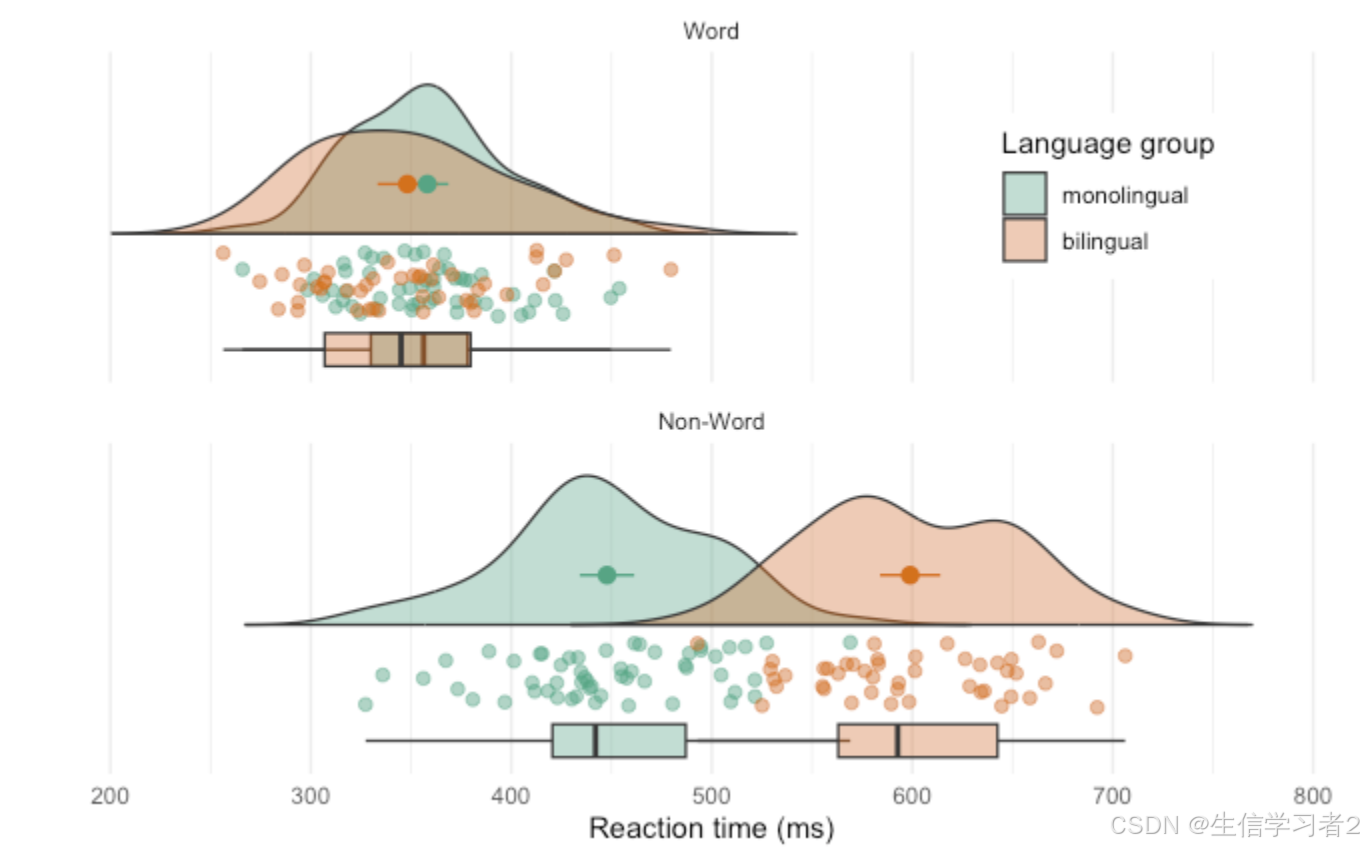
科研绘图系列：R语言雨云图（Raincloud plot）
介绍 雨云图（Raincloud plot）是一种数据可视化工具，它结合了多种数据展示方式，旨在提供对数据集的全面了解。雨云图通常包括以下几个部分： 密度图（Density plot）：表示数据的分布情况，密度图的曲线可以展示数据在不同数值区间的密度。箱线图（Box plot）：显示数据的中…...
优化教学流程和架构：构建高效学习环境的关键步骤
在教育领域，设计和优化教学流程和架构是提高学习效果和学生参与度的关键。本文将探讨如何通过合理的教学流程和有效的架构来构建一个高效的学习环境。 ### 1. 理解教学流程和架构的重要性 教学流程指的是教学活动的组织和顺序，而教学架构则是指支持教学…...
js | this 指向问题
https://juejin.cn/post/6844904083707396109 任何函数运行的时候，都会创建一个context对象，context对象有一个this对象，在运行的时候决定。任何函数都对应一个reference类结构体（具体叫啥有点忘了），简单就…...
《昇思 25 天学习打卡营第 15 天 | 基于MindNLP+MusicGen生成自己的个性化音乐 》
《昇思 25 天学习打卡营第 15 天 | 基于MindNLPMusicGen生成自己的个性化音乐 》 活动地址：https://xihe.mindspore.cn/events/mindspore-training-camp 签名：Sam9029 MusicGen概述 MusicGen是由Meta AI的Jade Copet等人提出的一种基于单个语言模型&…...
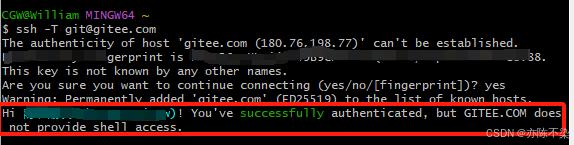
Gitee 使用教程1-SSH 公钥设置
一、生成 SSH 公钥 1、打开终端（Windows PowerShell 或 Git Bash），通过命令 ssh-keygen 生成 SSH Key： ssh-keygen -t ed25519 -C "Gitee SSH Key" 随后摁三次回车键（Enter） 2、查看生成的 SSH…...
理解Cookie、Session和Token
在现代Web开发中，用户身份认证和会话管理是至关重要的部分。理解Cookie、Session和Token的区别和应用场景，有助于我们设计出更加安全和高效的Web应用。本文将详细探讨这三者的工作原理、优缺点以及使用场景。 1. Cookie 1.1 什么是Cookie？ …...
概率论原理精解【1】
文章目录 测度概述集类笛卡尔积定义例子 多集合的笛卡尔积定义计算方法注意事项 有限笛卡尔积的性质1. 定义2. 性质2.1 基数性质2.2 空集性质2.3 不满足交换律2.4 不满足结合律2.5 对并和交运算满足分配律 3. 示例4. 结论 参考链接 测度 概述 所谓测度，通俗的讲就…...
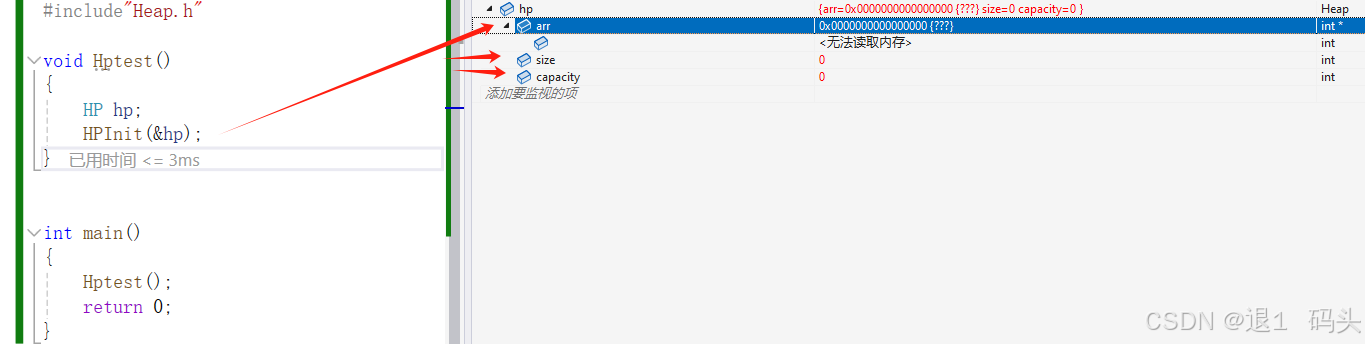
数据结构（二叉树-1）
文章目录 一、树 1.1 树的概念与结构 1.2 树的相关术语 1.3 树的表示 二、二叉树 2.1 二叉树的概念与结构 2.2特殊的二叉树 满二叉树 完全二叉树 2.3 二叉树的存储结构 三、实现顺序结构二叉树 3.1 堆的概念与结构 3.2 堆的实现 Heap.h Heap.c 默认初始化堆 堆的销毁 堆的插入 …...
MPNet：旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块（MBFM） 2.2 残差注意力金字塔模块（RAPM） 2.2.1 空间金字塔注意力（SPA） 2.2.2 金字塔残差块（PRBlock） 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...
基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能，多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统，涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能，适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...
LLM基础1_语言模型如何处理文本
基于GitHub项目：https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken：OpenAI开发的专业"分词器" torch：Facebook开发的强力计算引擎，相当于超级计算器 理解词嵌入：给词语画"…...
前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包（Closure）？闭包有什么应用场景和潜在问题？2.解释 JavaScript 的作用域链（Scope Chain） 二、原型与继承3.原型链是什么？如何实现继承&a…...
自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效，它能挖掘数据中的时序信息以及语义信息，但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN，但是…...
06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性：使神经网络可学习复杂模式控制输出范围：如Sigmoid将输出限制在(0,1)梯度传递：影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...
使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域，向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能，能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作，并通过具体…...
LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣（LeetCode） 思路 右视图是指从树的右侧看，对于每一层，只能看到该层最右边的节点。实现思路是： 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...
Python+ZeroMQ实战：智能车辆状态监控与模拟模式自动切换
目录 关键点 技术实现1 技术实现2 摘要： 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式（自动驾驶、人工驾驶、远程驾驶、主动安全），并通过实时消息推送更新车…...
作为测试我们应该关注redis哪些方面
1、功能测试 数据结构操作：验证字符串、列表、哈希、集合和有序的基本操作是否正确 持久化：测试aof和aof持久化机制，确保数据在开启后正确恢复。 事务：检查事务的原子性和回滚机制。 发布订阅：确保消息正确传递。 2、性…...