洛谷2月普及组(月赛)
🌼小宇(治愈版) - 刘大拿 - 单曲 - 网易云音乐
OI赛制且难度对标蓝桥杯省赛(😥真难,第三题做了几百年,第四题只敢骗骗分)
花了10块钱🙃 买官网的思路,结果还是习惯自己硬磕,别人的思路根本不想看,还不如自己百度
切记切记,OI赛制是部分分 + 无反馈
所以骗分很重要
骗分 = 样例 + 模拟 + 暴力
养成先测试再提交的好习惯,否则,你以为你天王盖地虎,原来是个二百五
👊总结
总结写在前头
1,骗分 = 样例 + 模拟 + 暴力
2,不论是codeforces还是洛谷,只做对样例,不给分,盲猜改革后的蓝桥杯也没分
3,不论是codeforces还是洛谷,凡是和数字有关的,都和奇偶数规律有着千丝万缕的关系
4,第三题,AC 100%需要(邻接表 + STL的priority_queue + Dijkstra),我还有邻接表没学,先留个坑,日后有时间回来做
目录
👊总结
👊一,P9063 [yLOI2023] 分解只因数
🌼解法1 AC 100%
🌼解法2 AC 90%
🌼解法3 AC 60%
👊二,P9064 [yLOI2023] 苦竹林
🌼AC 30%
🌼AC 100%
👊三,P9065 [yLOI2023] 云梦谣
🌼AC 5%
👊四,P9066 [yLOI2023] 腐草为萤
🌼AC 5%
👊一,P9063 [yLOI2023] 分解只因数
P9063 [yLOI2023] 分解只因数 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
通过率 10%
难度:入门


首先要理解n不一定需要相乘得到的,比如 11 == 11,3 == 3,也可以是等本身,所以3和11也是只因数,一开始钻牛角尖了
🌼解法1 AC 100%
因数中只要存在偶数,也就是不全为奇数,累乘的n就是偶数
所以,当n是偶数,说明质因数中存在偶数;当n是奇数,质因数全为奇数
所以n是奇数时输出"Yes",n是偶数时输出"No"
#include<iostream>
#include<cstdio> //scanf()
using namespace std;
typedef long long LL;
bool check(LL n)
{if(n % 2 == 1) return true;return false;
}
int main()
{int t;scanf("%d", &t);while(t) {LL n;scanf("%lld", &n);if(check(n)) cout<<"Yes"<<endl;else cout<<"No"<<endl;t--;}return 0;
}
5
2
No
3
Yes
4
No
6
No
9
Yes4
12
No
123
Yes
1234
No
12345
Yes
🌼解法2 AC 90%
常规解法,对质数,因数不熟练的新手,耗时比较久,比如我
质数:能被1和本身整除的数
1,遍历到m的平方差,即 i * i <= m
2,m % i == 0,则 m 不是质数
#include<iostream>
#include<cstdio> //scanf()
using namespace std;
typedef long long LL;
bool check(LL n)
{int flag = 1;if(n == 1 || n == 2) return false; //1不是质数, 2是偶数int m;for(m = 2; m * m <= n; ++m) {for(int i = 2; i * i <= m; ++i)if(m % i == 0) {flag = 0; //m不是质数break;}if(flag && n % m == 0) //m是质数且是n的因子if(m % 2 == 0) return false; //因子是偶数}return true;
}
int main()
{int t;scanf("%d", &t);while(t) {LL n;scanf("%lld", &n);if(check(n)) cout<<"Yes"<<endl;else cout<<"No"<<endl;t--;}return 0;
}
第10个样例,Time Limit Exceeded,TLE了
输入3,由于 m * m <= 3连 m = 2都不满足,所以没经过判断,直接return true;了
🌼解法3 AC 60%
投机取巧,骗分的方法,关键是快!只用了5分钟,分也不少
#include<iostream>
#include<cstdio> //scanf()
using namespace std;
typedef long long LL;
bool check(LL n)
{if(n == 2 || n == 4 || n == 6|| n == 8 || n == 10 || n == 12 || n == 14|| n == 16 || n == 18 || n == 20)return false;if(n == 3 || n == 5 || n == 9 || n == 15 || n == 21|| n == 7 || n == 11 || n == 13 || n == 17 || n == 19)return true;
}
int main()
{int t;scanf("%d", &t);while(t) {LL n;scanf("%lld", &n);if(check(n)) cout<<"Yes"<<endl;else cout<<"No"<<endl;t--;}return 0;
}
👊二,P9064 [yLOI2023] 苦竹林
P9064 [yLOI2023] 苦竹林 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
通过率 14%
难度:普及-

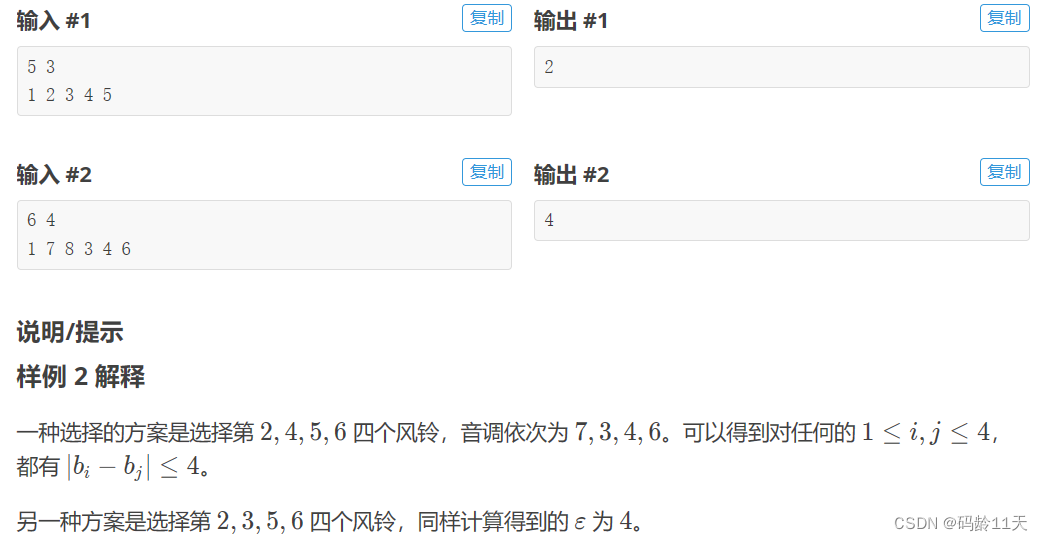

1,先对数组a从小到大排序
2,尺取法,对连续的m个数遍历,每次更新Min
将Min与 (尺取的最后一个元素 - 尺取的第一个元素) 作比较
复杂度O(logn + n - m) ;logn表示log2n,是快排的复杂度
不会尺取法的看这里
尺取法(图文解析、初学推荐)_小白小郑的博客-CSDN博客_尺取法
算法基础----尺取法(双指针)_jkaliang的博客-CSDN博客
1,尺取法是算法竞赛中,常用的优化技巧
2,它比暴力枚举区间的效率高很多(特别是数据量大时,比如10^6),是一种高效枚举区间的方法,用于求取有一定限制的区间个数或最短区间
3,本题中通过左边界右移,右边界右移的方法,找到满足区间,并用Min保留相减最小值(也就是题目中的ε)
注意!!!OI赛制没有反馈,所以首先要自己想多点全面,偏门的案例
来验证代码,不然很可能就是信心满满 = AC 30%
先别急着提交,下面我展示5组测试样例
10 6
1 8 26 33 41 17 102 27 11 5
226 2
1 4 9 12 13 15
15 3
1 2 3 4 5
26 4
1 7 8 3 4 6
410 4
120 240 550 1101 1199 2012 3312 5520 5523 5524
959然后,,,第一次30%
🌼AC 30%
#include<iostream>
#include<cstdio> //scanf()
#include<algorithm> //sort()
using namespace std;
int a[100010];
int main()
{int n, m;scanf("%d%d", &n, &m);for(int i = 0; i < n; ++i)scanf("%d", &a[i]); //读入数据sort(a, a + n);int Min = 1e8; //大坑for(int i = m - 1; i < n; ++i) {int j = i - (m - 1); //此时[j, i]刚好m个数if(a[i] - a[j] < Min)Min = a[i] - a[j];}cout<<Min;return 0;
}
思路很清晰啊,怎么会错呢?原来是第13行,初始最小值设置成1e8了
而题目原文却是:
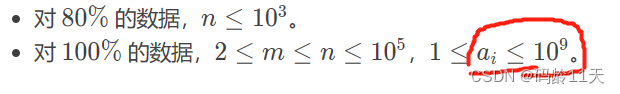
所以,设置最小值,直接将题目中的范围粘贴过来好了。。
最大值一般设为负数
毕竟70%的样例都是大于1e8的
🌼AC 100%
#include<iostream>
#include<cstdio> //scanf()
#include<algorithm> //sort()
using namespace std;
int a[100010];
int main()
{int n, m;scanf("%d%d", &n, &m);for(int i = 0; i < n; ++i)scanf("%d", &a[i]); //读入数据sort(a, a + n);int Min = 1e9; //大坑for(int i = m - 1; i < n; ++i) {int j = i - (m - 1); //此时[j, i]刚好m个数if(a[i] - a[j] < Min)Min = a[i] - a[j];}cout<<Min;return 0;
}
复杂度O(n * logn),也就是快排的复杂度,后面的O(n - m)相比O(nlogn)可忽略
👊三,P9065 [yLOI2023] 云梦谣
P9065 [yLOI2023] 云梦谣 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
题目有点长😅,通过率 6%
难度:普及+/提高


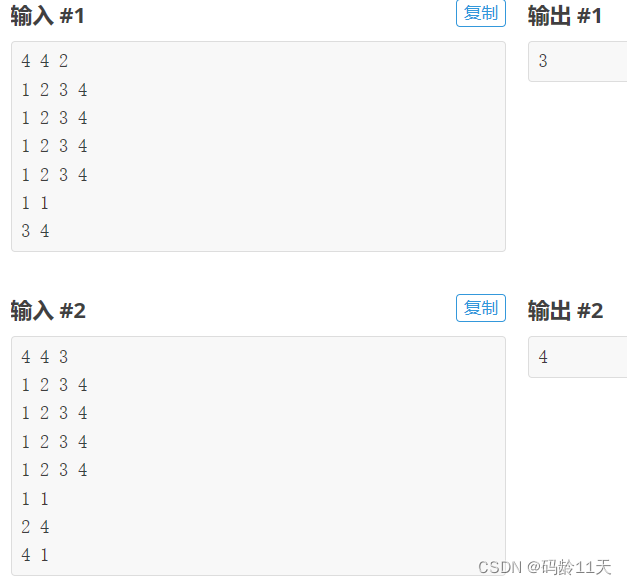
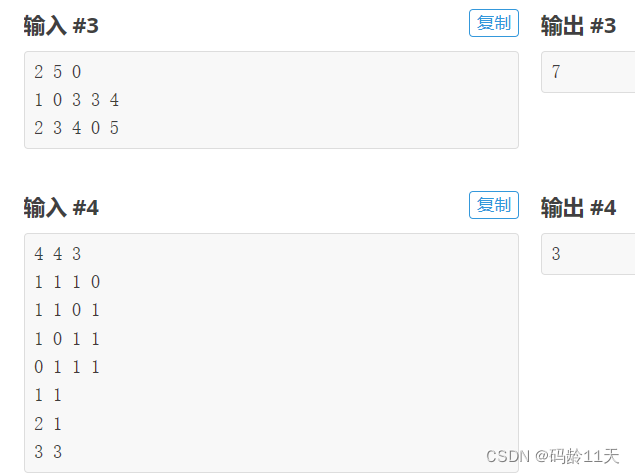


1,读入数据较多,我们用scanf不用cin
2,点与点之间路径一样,都为1,我觉得用dfs比Dijkstra好做
所以就是纯dfs(后面证明dfs❌)
然鹅。。第一次就AC 5% ,而且我四个测试样例都对了,,,,
🌼AC 5%
#include<iostream>
#include<cstdio> //scanf()
using namespace std;
int a[3010][3010], book[3010][3010], b[3010][3010];
int fly[3010][3010], ans = 3000;
int n, m, k;void dfs(int x, int y, int step)
{int next[4][2] = { //方向数组, 循环得到下一步坐标{-1, 0}, //上{1, 0}, //下{0, -1}, //左{0, 1}}; //右//dfs第一步: 遍历int tx, ty; //临时变量for(int i = 0; i < 4; ++i) {tx = x + next[i][0]; //0表示每行第1个元素ty = y + next[i][1]; //1表示每行第2个元素//越界if(tx < 1 || ty < 1 || tx > n || ty > m)continue; //跳出本次循环//非障碍物且未走过if(a[tx][ty] != 0 && book[tx][ty] != 1) {book[tx][ty] = 1; //标记dfs(tx, ty, step + 1); //递归book[tx][ty] = 0; //取消标记}}//找到目标if(x == n && y == m) {ans = min(ans, step); //更新return; //返回上一步}
}int main()
{scanf("%d%d%d", &n, &m, &k);for(int i = 1; i <= n; ++i)for(int j = 1; j <= m; ++j)scanf("%d", &a[i][j]); //读入数据int r, t;for(int i = 0; i < k; ++i) {scanf("%d%d", &r, &t);fly[r][t] = 1; //可飞行}book[1][1] = 1; //初始已走过//得到全程走的最小值dfs(1, 1, 0);//得到飞的最小值for(int i = 1; i <= n; ++i)for(int j = 1; j <= m; ++j)if(fly[i][j] == 1) { //可飞if(a[i][j] != a[1][1]) //高度不同dfs(i, j, 2);else //高度一样dfs(i, j, 1);}cout<<ans;return 0;
}
做了2小时才AC 5%,,,666
问题在哪呢?
1,dfs就不适合最短路(指数级复杂度),一般用Dijksta的堆优化求单源最短路
2,漏了,如果到达不了,要输出"-1"的情况(补上这个就AC 10%)
3,代码里默认(1, 1)能飞,这是错误的
因为只是样例中的(1, 1)能飞,存在(1, 1)不能飞,走几步才能飞的情况
最后的
cout<<ans;改成
if(ans == 3000) cout<<-1;
else cout<<ans;就AC 10%
好的,下一步考虑用stl的优先队列priority_queue优化Dijkstra
这已经是最简单的做法了,如果能成,估计只需要60行
不行了,堆优化的Dijkstra虽然可以用stl的最大最小值优先队列(大小根堆),但是还得学习什么“链式前向星”(也就是静态的邻接表),《啊哈算法》里有讲邻接表,但是我想先放放,先把简单的,更易拿分的掌握了,两个月以内再回来克服它
2023/02/12 👆👆👆
10:27留坑
👊四,P9066 [yLOI2023] 腐草为萤
P9066 [yLOI2023] 腐草为萤 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
难度:提高+/省选-
题目就不放了,感兴趣的,自己去模拟 + 样例骗分吧
🌼AC 5%
#include <iostream>
using namespace std;
int a[110], b[110];
int main()
{int n;cin>>n;for(int i = 0; i < n; ++i)cin>>a[i]; //初始位置for(int i = 0; i < n; ++i)cin>>b[i]; //亮度for(int i = 1; i < n; ++i) {if(b[i] > b[i - 1])cout<<a[i]<<" "<<0;else if(b[i] == b[i - 1])cout<<0<<" "<<0;elsecout<<0<<" "<<a[i - 1];}return 0;
}
相关文章:

洛谷2月普及组(月赛)
🌼小宇(治愈版) - 刘大拿 - 单曲 - 网易云音乐 OI赛制且难度对标蓝桥杯省赛(😥真难,第三题做了几百年,第四题只敢骗骗分) 花了10块钱🙃 买官网的思路,结果…...

【博学谷学习记录】超强总结,用心分享 | 架构师 Spring源码学习总结
文章目录Spring的循环依赖1.循环依赖的定义&&原因2.循环依赖的场景1.构造器注入引起循环依赖2.Field属性setter注入的循环依赖3.循环依赖解决思路4.三级缓存5.面试题[三级缓存]AOP源码深度剖析概述Spring AOP的前世今生实现机制**JDK 动态代理****CGLIB 代理**流程总结…...
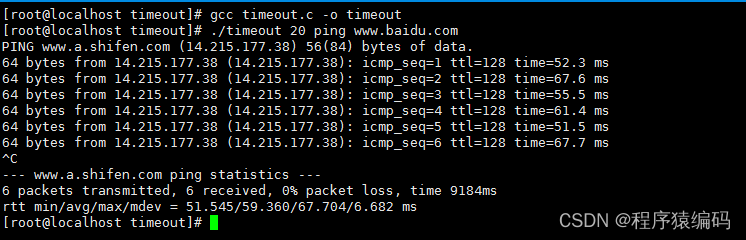
Linux C/C++ timeout命令实现(运行具有时间限制)
Linux附带了大量命令,每个命令都是唯一的,并在特定情况下使用。Linux timeout命令的一个属性是时间限制。可以为任何命令设置时间限制。如果时间到期,命令将停止执行。 如何使用timeout命令 我们将解释如何使用Linux timeout命令 timeout […...
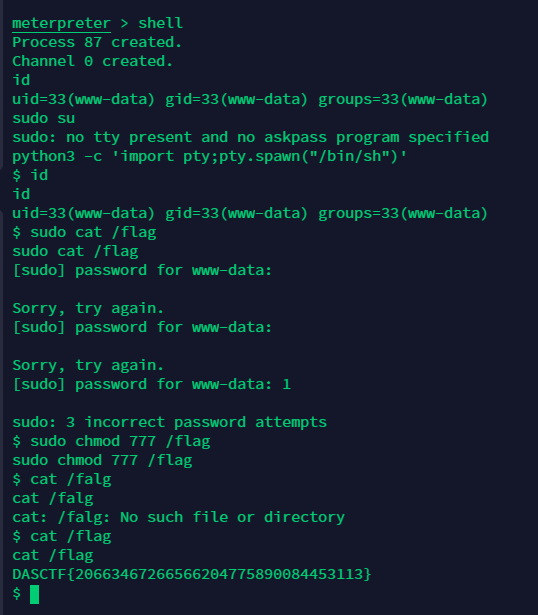
西湖论剑初赛web wp
Node Magical Login 简单的js代码审计。 Flag分成了两部分。 第一部分: 这里就简单的判断了一下user是否等于admin,直接绕过。 第二部分: checkcode ! “aGr5AtSp55dRacer”,让其为真,利用数组绕过。 Flag为&#x…...

【YOLOv8/YOLOv7/YOLOv5系列算法改进NO.55】融入美团最新QARepVGG
文章目录 前言一、解决问题二、基本原理三、添加方法四、总结前言 作为当前先进的深度学习目标检测算法YOLOv8,已经集合了大量的trick,但是还是有提高和改进的空间,针对具体应用场景下的检测难点,可以不同的改进方法。此后的系列文章,将重点对YOLOv8的如何改进进行详细…...

Flutter Windows端打包并生成可安装文件流程
Windows打包 1.首先安装visual Studio 下载地址:https://visualstudio.microsoft.com/zh-hans/ 下载成功后按照下图勾选桌面应用和移动应用下的使用C的桌面开发,勾选右侧安装详细信息中的windows 11/10 sdk 中的任意一个完成安装即可 2.打包Windows …...

凸优化学习:PART3凸优化问题(持续更新)
凸优化问题 凸优化问题的广义定义: 目标函数为凸函数约束集合为凸集 一、优化问题 基本用语 一般优化问题的描述: minimizef0(x)subject to fi(x)⩽0,i1,⋯,mhi(x)0,i1,⋯,p(1)\begin{array}{ll} \operatorname{minimize} & f_0(x) \\ \text { s…...
)
[ue4] 着色器绑定(Shader Binding)
当我们在ue4中制作了一个美术材质之后,引擎本身会为我们做很多事情,它会把结点翻译为hlsl,生成多个shader变体,并在多个mesh pass中去选择性的调用所需的shader,其中一个重要的过程就是获取shader绑定的数据。 本文将主…...

Rust语言之迭代器
文章目录Rust迭代器Rust迭代器的实现Iterator特型IntoIterator特型for循环与迭代器迭代器类型再看for循环实现自定义迭代器方式一方式二相关参考Rust迭代器 Rust语言内置了迭代器模式,用于实现对一个项的序列进行特定的处理,通常配合for循环使用。当我们…...
TreeSet 与 TreeMap And HashSet 与 HashMap
目录 Map TreeMap put()方法 : get()方法 : Set> entrySet() (重) : foreach遍历 : Set 哈希表 哈希冲突 : 冲突避免 : 冲突解决 ---- > 比散列(开放地址法) : 开散列 (链地址法 . 开链法) 简介 : 在Java中 , TreeSet 与 TreeMap 利用搜索树实现 Ma…...
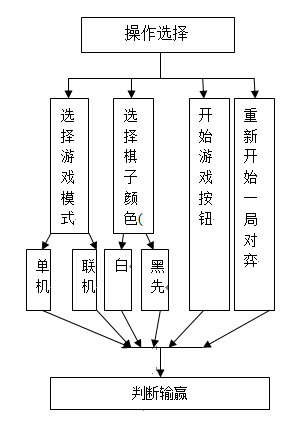
Java围棋游戏的设计与实现
技术:Java等摘要:围棋作为一个棋类竞技运动,在民间十分流行,为了熟悉五子棋规则及技巧,以及研究简单的人工智能,决定用Java开发五子棋游戏。主要完成了人机对战和玩家之间联网对战2个功能。网络连接部分为S…...

第七十三章 使用 irisstat 实用程序监控 IRIS - 使用选项运行 irisstat
文章目录第七十三章 使用 irisstat 实用程序监控 IRIS - 使用选项运行 irisstat使用选项运行 irisstatirisstat Options第七十三章 使用 irisstat 实用程序监控 IRIS - 使用选项运行 irisstat 使用选项运行 irisstat 不带选项运行 irisstat 会生成基本报告。通常,…...

【博客619】PromQL如何实现Left joins以及不同metrics之间的复杂联合查询
PromQL如何实现Left joins以及不同metrics之间的复杂联合查询 1、场景 我们需要在PromQL中实现类似SQL中的连接查询: SELECT a.value*b.value, * FROM a, b2、不同metrics之间的复杂联合查询 瞬时向量与瞬时向量之间进行数学运算: 例如:根…...
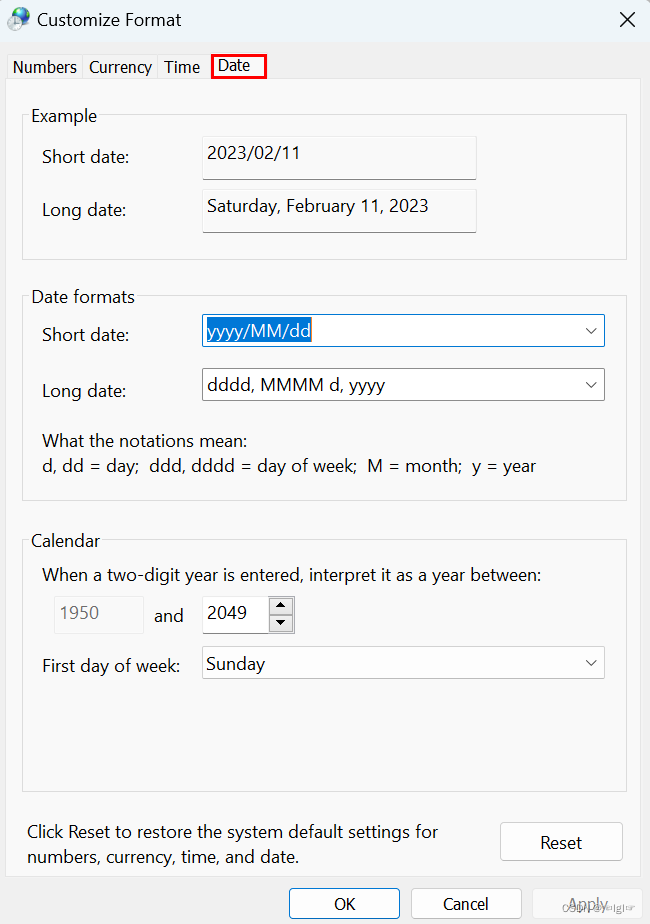
Win11自定义电脑右下角时间显示格式
Win11自定义电脑右下角时间显示格式 一、进入附加设置菜单 1、进入控制面板,选择日期和时间 2、选择修改日期和时间 3、选择修改日历设置 4、选择附加设置 二、自定义时间显示出秒 1、在选项卡中,选时间选项卡 2、在Short time的输入框中输入H:m…...
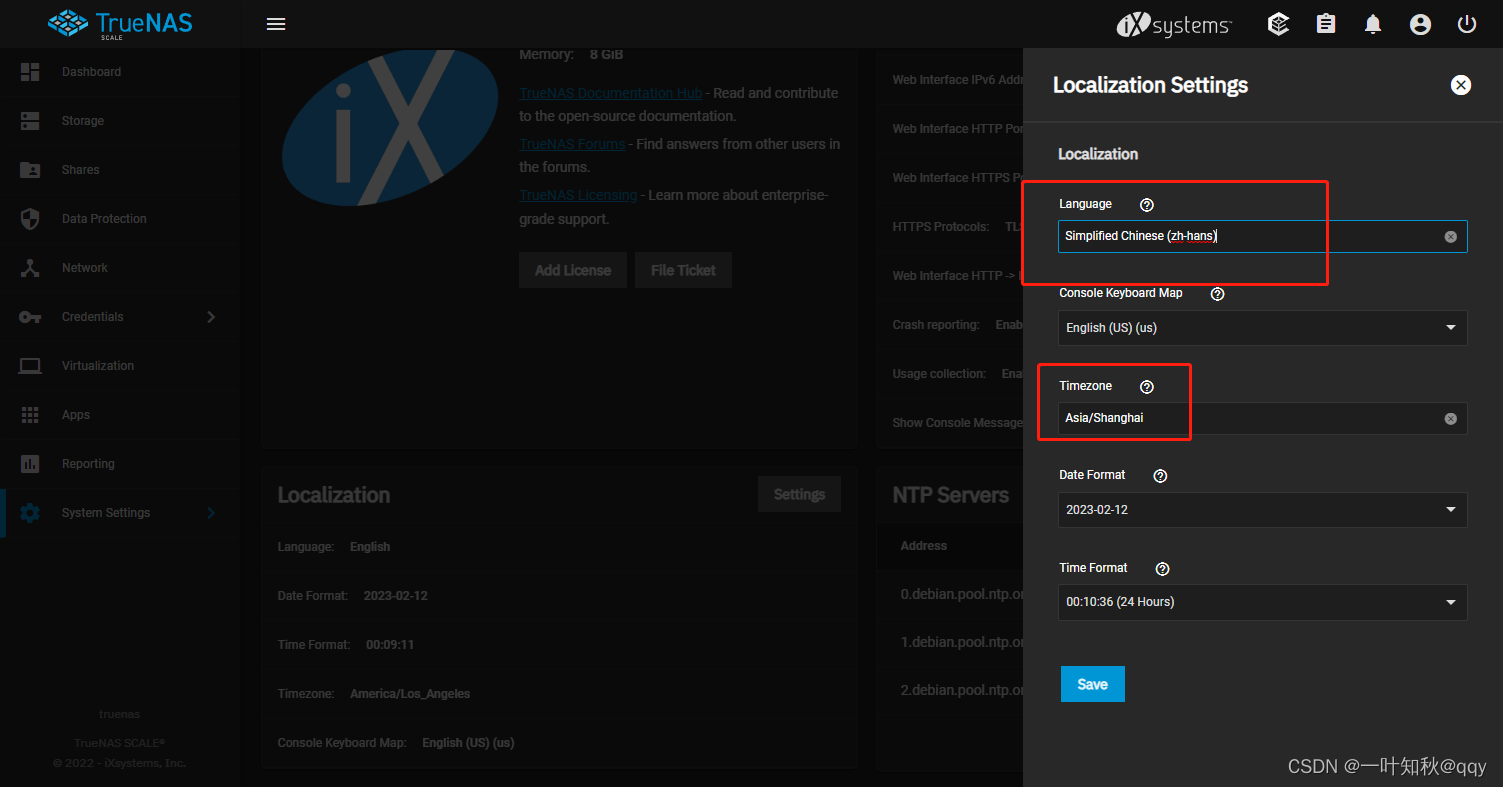
TrueNas篇-trueNas Scale安装
安装TrueNAS Scale 在尝试trueNas core时发下可以成功安装,但是一直无法成功启动,而且国内对我遇见的错误几乎没有案例,所以舍弃掉了,而且trueNas core是基于Linux的,对Linux的生态好了很多,还可以可以在t…...
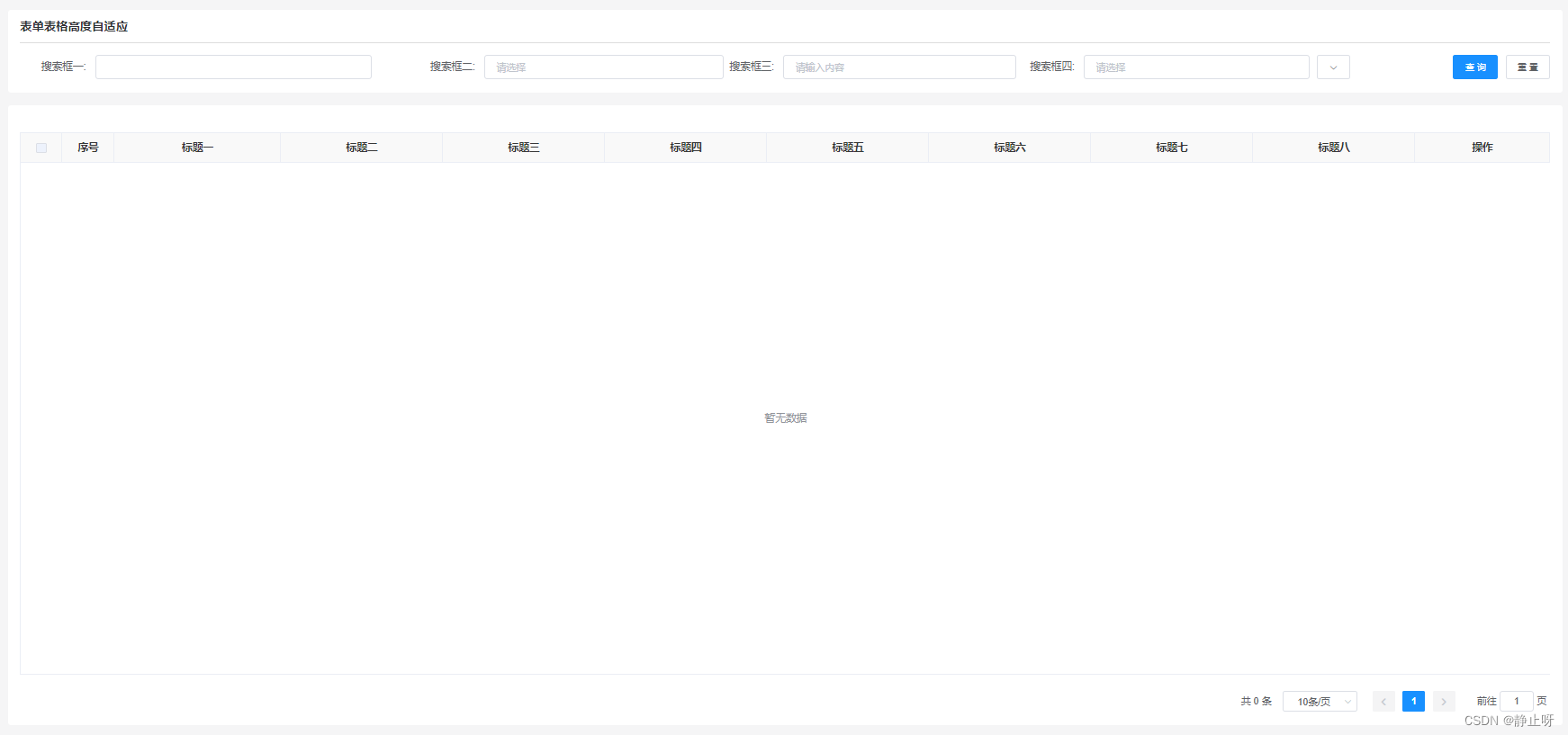
element表单搜索框与表格高度自适应
一般在后台管理系统中,表单搜索框和表格的搭配是非常常见的,如下所示: 在该图中,搜索框有五个,分为了两行排列。但根据大多数的UI标准,搜索框默认只显示一行,多余的需要进行隐藏。此时的页面被…...

MySQL使用技巧整理
title: MySQL使用技巧整理 date: 2021-04-11 00:00:00 tags: MySQL categories:数据库 重建索引 索引可能因为删除,或者页分裂等原因,导致数据页有空洞,重建索引的过程会创建一个新的索引,把数据按顺序插入,这样页面…...

七大设计原则之里氏替换原则应用
目录1 里氏替换原则2 里氏替换原则应用1 里氏替换原则 里氏替换原则(Liskov Substitution Principle,LSP)是指如果对每一个类型为 T1 的对象 o1,都有类型为 T2 的对象 o2,使得以 T1 定义的所有程序 P 在所有的对象 o1 都替换成 o2 时,程序 P…...

1行Python代码去除图片水印,网友:一干二净
大家好,这里是程序员晚枫。 最近小明在开淘宝店(店名:爱吃火锅的少女),需要给自己的原创图片加水印,于是我上次给她开发了增加水印的功能:图片加水印,保护原创图片,一行…...
)
Connext DDS属性配置参考大全(2)
DDSSecure安全com.rti.servcom.rti.serv.load_plugin...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...
