Notepad++换安装路径之后,右键打开方式报错:Windows无法访问指定设备、路径或文件。你可能没有适当的权限访问该项目。的处理方法
把Notepad++添加到右键打开方式,可以参考下面的3篇文章添加:
https://blog.csdn.net/xiaoerbuyu1233/article/details/88287747
https://blog.csdn.net/qq_44000337/article/details/120277317
https://www.cnblogs.com/zhrngM/p/12899026.html
这里主要是另一个问题,因为把Notepad++的目录换了,因而引发了一些问题,比如:快捷方式失败(右键快捷方式,设置位置为新的路径即可),文件右键图标丢失,右键打开报错。
错误信息如下:Windows无法访问指定设备、路径或文件。你可能没有适当的权限访问该项目。
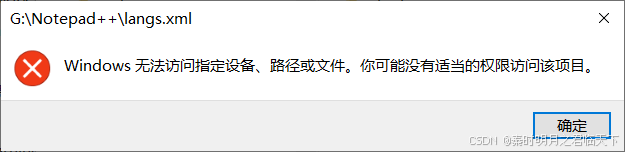
我想着按照上面添加的步骤,直接去更改成新的路径应该就可了。但是发现有点问题,改完之后右键的icon可以正常显示了,但是打开还是报一样的错。
反复检查还是没有问题,然后尝试新增一个,没想到还真就成功了,然后把这两个注册表导出来对比了一下(右边是新增的):
旧的:
Windows Registry Editor Version 5.00[HKEY_CLASSES_ROOT\*\shell\Open With Notepad++]
"Icon"="G:\\Notepad++\\notepad++.exe"[HKEY_CLASSES_ROOT\*\shell\Open With Notepad++\Command]
@="\"G:\\Notepad++\\notepad++.exe\" \"%1\""
新的:
Windows Registry Editor Version 5.00[HKEY_CLASSES_ROOT\*\shell\Edit with Notepad++]
@=""
"icon"="G:\\Notepad++\\notepad++.exe"[HKEY_CLASSES_ROOT\*\shell\Edit with Notepad++\command]
@="\"G:\\Notepad++\\notepad++.exe\" \"%1\""
对比图:

可以看到两者主要的区别就是:左边少了 @="",导致不能正常打开,但是我也搞不懂到底是怎么丢掉的……
所以就把旧的删掉,用新的。
相关文章:

Notepad++换安装路径之后,右键打开方式报错:Windows无法访问指定设备、路径或文件。你可能没有适当的权限访问该项目。的处理方法
把Notepad添加到右键打开方式,可以参考下面的3篇文章添加: https://blog.csdn.net/xiaoerbuyu1233/article/details/88287747 https://blog.csdn.net/qq_44000337/article/details/120277317 https://www.cnblogs.com/zhrngM/p/12899026.html 这里主要是…...

【Flutter 面试题】 使用成熟状态管理库的弊端有哪些?
【Flutter 面试题】 使用成熟状态管理库的弊端有哪些? 文章目录 写在前面口述回答补充说明写在前面 🙋 关于我 ,小雨青年 👉 CSDN博客专家,GitChat专栏作者,阿里云社区专家博主,51CTO专家博主。2023博客之星TOP153。 👏🏻 正在学 Flutter 的同学,你好! 😊 …...

Apache Commons技术详解
文章目录 简介官网链接原理基础使用Commons LangCommons Collections 高级使用Commons IOCommons Math 优缺点优点缺点 总结 简介 Apache Commons 是 Apache 软件基金会下的一个项目,旨在提供可重用的Java组件。这些组件覆盖了广泛的编程任务,从字符串处…...

怎样使用 Juicer tools 的 dump 命令将.hic文件转换为交互矩阵matrix计数文件 (Windows)
创作日志: 万恶的生信…一个scHiC数据集没有提供处理好的计数文件,需要从.hic转换。Github一个个好长的文档看了好久才定位到 juicer tools 的dump命令,使用起来比想象中简单。 一、下载Juicer tools 注意:使用Juicer tools的前提…...
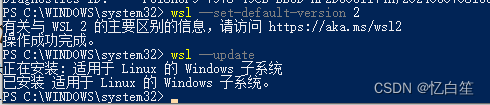
【Docker】Docker Desktop - WSL update failed
问题描述 Windows上安装完成docker desktop之后,第一次启动失败,提示:WSL update failed 解决方案 打开Windows PowerShell 手动执行: wsl --set-default-version 2 wsl --update...

基于rsync\unlink 等一套本机备份跨机备份历史备份清理shell 脚本
一 摘要 本文主要介绍一套本地备份、跨机器备份、历史备份清理脚本,使用场景如数据库备份等 二 环境 linux 系列系统 基本都支持,个别命令可能需要微调。 2.1 实验环境 [rootlocalhost rsync]# cat /etc/centos-release CentOS Linux release 7.9.2…...

使用nginx实现一个端口和ip访问多个vue前端
前言:由于安全组要求,前端页面只开放一个端口,但是项目有多个前端,此前一直使用的是一个前端使用单独一个端口进行访问,现在需要调整。 需要实现:这里以80端口为例,两个前端分别是:p…...

Linux云计算 |【第一阶段】SERVICES-DAY5
主要内容: 源码编译安装、rsync同步操作、inotify实时同步、数据库服务基础 实操前骤:(所需tools.tar.gz与users.sql) 1.两台主机设置SELinnx和关闭防火墙 setenforce 0 systemctl stop firewalld.service //停止防火墙 sy…...

IP第一次综合实验
一、实验拓扑 二、实验要求 1、R6为ISP,接口IP地址均为公有地址,该设备只能配置地址之后不能冉对其进行任何配置 2、R1-R5为局域网,私有Ip地址192.168.1.0/24,请合理分配 3、R1、82、R4,各有两个环回IP地址;R5,R6各…...

Could not load dynamic library ‘cudart64_100.dll‘
python代码报错 Could not load dynamic library cudart64_100.dll; dlerror: cudart64_100.dll not found 2024-07-22 14:19:21.931639: I tensorflow/stream_executor/cuda/cudart_stub.cc:29] Ignore above cudart dlerror if you do not have a GPU set up on your machine…...

四大引用——强软弱虚
目录 一、强引用 二、软引用 三、弱引用 四、虚引用 一、强引用 强引用是在程序代码之中普遍存在的,类似于“Object obj new Object()”,obj变量引用Object这个对象,就叫做强引用。当内存空间不足,Java虚拟机宁愿抛出OutOfMe…...

MySQL--索引(2)
InnoDB 1.索引类型 主键索引(Primary Key) 数据表的主键列使用的就是主键索引。 一张数据表有只能有一个主键,并且主键不能为 null,不能重复。 在 mysql 的 InnoDB 的表中,当没有显示的指定表的主键时,InnoDB 会自动先检查表中是…...

JVM类加载机制详解
Java在运行期才对类进行加载到内存、连接、初始化过程。这使得Java应用具有极高的灵活性和拓展性,可以依赖运行期进行动态加载和动态连接。 主要加载哪些?Java中的数据类型分为基本数据类型和引用数据类型,基本数据类型由虚拟机预先定义&…...

【MATLAB实战】基于UNet的肺结节的检测
数据: 训练过程图 算法简介: UNet网络是分割任务中的一个经典模型,因其整体形状与"U"相似而得名,"U"形结构有助于捕获多尺度信息,并促进了特征的精确重建,该网络整体由编码器,解码器以及跳跃连接三部分组成。 编码器由…...

Elasticsearch基础(五):使用Kibana Discover探索数据
文章目录 使用Kibana Discover探索数据 一、添加样例数据 二、数据筛选 三、保存搜索 使用Kibana Discover探索数据 一、添加样例数据 登录Kibana。在Kibana主页的通过添加集成开始使用区域,单击试用样例数据。 在更多添加数据的方式页面下方,单击…...

爬取百度图片,想爬谁就爬谁
前言 既然是做爬虫,那么肯定就会有一些小心思,比如去获取一些自己喜欢的资料等。 去百度图片去抓取图片吧 打开百度图片网站,点击搜索xxx,打开后,滚动滚动条,发现滚动条越来越小,说明图片加载…...

HTTP 缓存
缓存 web缓存是可以自动保存常见的文档副本的HTTP设备,当web请求抵达缓存时,如果本地有已经缓存的副本,就可以从本地存储设备而不是从原始服务器中提取这个文档。使用缓存有如下的优先。 缓存减少了冗余的数据传输缓存环节了网络瓶颈的问题…...

设计模式实战:图形编辑器的设计与实现
简介 本篇文章将介绍如何设计一个图形编辑器系统,系统包括图形对象的创建、组合、操作及撤销等功能。我们将通过这一项目,应用命令模式、组合模式和备忘录模式来解决具体的设计问题。 问题描述 设计一个图形编辑器系统,用户可以创建并操作图形对象,将多个图形对象组合成…...

.NET 情报 | 分析某云系统添加管理员漏洞
01阅读须知 此文所提供的信息只为网络安全人员对自己所负责的网站、服务器等(包括但不限于)进行检测或维护参考,未经授权请勿利用文章中的技术资料对任何计算机系统进行入侵操作。利用此文所提供的信息而造成的直接或间接后果和损失…...

vue检测页面手指滑动距离,执行回调函数,使用混入的语法,多个组件都可以使用
mixin.ts 定义滑动距离的变量和检测触摸开始的方法,滑动方法,并导出两个方法 sendTranslateX.value > 250 && sendTranslateY.value < -100是向上滑动,满足距离后执行回调函数func,并在一秒内不再触发,一…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

python爬虫——气象数据爬取
一、导入库与全局配置 python 运行 import json import datetime import time import requests from sqlalchemy import create_engine import csv import pandas as pd作用: 引入数据解析、网络请求、时间处理、数据库操作等所需库。requests:发送 …...

认识CMake并使用CMake构建自己的第一个项目
1.CMake的作用和优势 跨平台支持:CMake支持多种操作系统和编译器,使用同一份构建配置可以在不同的环境中使用 简化配置:通过CMakeLists.txt文件,用户可以定义项目结构、依赖项、编译选项等,无需手动编写复杂的构建脚本…...

【堆垛策略】设计方法
堆垛策略的设计是积木堆叠系统的核心,直接影响堆叠的稳定性、效率和容错能力。以下是分层次的堆垛策略设计方法,涵盖基础规则、优化算法和容错机制: 1. 基础堆垛规则 (1) 物理稳定性优先 重心原则: 大尺寸/重量积木在下…...

6️⃣Go 语言中的哈希、加密与序列化:通往区块链世界的钥匙
Go 语言中的哈希、加密与序列化:通往区块链世界的钥匙 一、前言:离区块链还有多远? 区块链听起来可能遥不可及,似乎是只有密码学专家和资深工程师才能涉足的领域。但事实上,构建一个区块链的核心并不复杂,尤其当你已经掌握了一门系统编程语言,比如 Go。 要真正理解区…...

机器学习的数学基础:线性模型
线性模型 线性模型的基本形式为: f ( x ) ω T x b f\left(\boldsymbol{x}\right)\boldsymbol{\omega}^\text{T}\boldsymbol{x}b f(x)ωTxb 回归问题 利用最小二乘法,得到 ω \boldsymbol{\omega} ω和 b b b的参数估计$ \boldsymbol{\hat{\omega}}…...

链式法则中 复合函数的推导路径 多变量“信息传递路径”
非常好,我们将之前关于偏导数链式法则中不能“约掉”偏导符号的问题,统一使用 二重复合函数: z f ( u ( x , y ) , v ( x , y ) ) \boxed{z f(u(x,y),\ v(x,y))} zf(u(x,y), v(x,y)) 来全面说明。我们会展示其全微分形式(偏导…...
