使用uniapp开发小程序(基础篇)
本文章只介绍微信小程序的开发流程,如果需要了解其他平台的开发的流程的话,后续根据情况更新相应的文章,也可以根据uniapp官网的链接了解不同平台的开发流程
HBuilderX使用:https://uniapp.dcloud.net.cn/quickstart-hx.html
开发工具
开始之前,开发者需先下载安装如下工具:
HBuilderX:官方IDE下载地址
微信开发者工具:官方下载地址
这里的前提是已安装nodejs,如果没有安装请安装。因为需要本地运行js文件
node安装:可以直接在官方下载地址安装 (不建议) 官方下载地址
使用nvm进行node版本管理安装 (个人建议) 官方下载Github地址
可以切换node版本,可能开发过程中会出现某一些库在一些node版本中不兼容,切换系统node版本方便
nvm version # 查看 nvm 版本,version 可简写成 小v
nvm v # 显示 node 是运行在 32 位还是 64 位
nvm on # 开启 node.js 版本管理
nvm off # 关闭 node.js 版本管理
nvm arch
nvm ls # 查看版本安装所有版本
nvm ls-remote # 查看远程所有的 Node.js 版本
nvm install 17.0.0 # 安装指定的 Node.js 版本
nvm use 17.0.0 # 使用指定的 Node.js 版本
nvm alias default 17.0.0 # 设置默认 Node.js 版本
nvm alias dev 17.0.0 # 设置指定版本的别名,如将 17.0.0 版本别名设置为 dev
nvm uninstall [version] # 卸载指定版本 node
nvm use [version] # 使用指定版本 node修改nvm的镜像源地址
问题:为什么要配置镜像?
答:配置完国内的镜像后,npm install xxx 的下载速度会很快!
在 nvm 的安装路径下,找到 settings.txt,在后面加上这两行,设置国内淘宝镜像源:

node_mirror: https://npmmirror.com/mirrors/node/
npm_mirror: https://npmmirror.com/mirrors/npm/
修改 npm 默认镜像源
npm是node管理下载模块的工具,如果在项目使用的过程中需要一些依赖,就可以使用npm命令进行安装
类似于python编译器中的pip包管理工具
npm install 模块名 --registry=http://registry.npmmirror.com
npm源永久替换为淘宝的镜像源
- 命令修改
npm config set registry http://registry.npmmirror.com
- 文件修改
打开.npmrc文件(~nodejs\node_modules\npm\npmrc,没有的话可以使用git命令行建一个( touch .npmrc),用cmd命令建会报错)增加 registry=http://registry.npmmirror.com 即可。(node安装目录)
如果需要恢复成原来的官方地址只需要执行如下命令:
npm config set registry https://registry.npmjs.org
也可以使用cnpm命令,不修改npm(这里不介绍)
由于npm的源在国外,所以国内用户使用起来各种不方便,可能会出现无法访问,发生异常,或者下载缓慢等问题。为此,淘宝搭建了 cnpm(中国 npm 镜像的客户端),它是一个完整的 npmjs.org 镜像,你可以用此代替官方版本
uniapp小程序
配置
-
uniapp小程序运行到小程序模拟器前应该在创建的uniapp项目的配置文件
manifest.json中配置小程序appid

-
小程序模拟器路径配置
工具->设置->运行设置 下找到小程序运行配置选择已安装的微信开发者工具位置

-
配置node路径
工具->设置->运行设置 下找到node运行配置

-
在微信开发者工具上面开启服务端口

运行
在微信开发者工具里运行:进入hello-uniapp项目,点击工具栏的运行 -> 运行到小程序模拟器 -> 微信开发者工具,即可在微信开发者工具里面体验uni-app。

uniapp会生成小程序的应用文件,文件目录在项目的 unpackage\dist\dev\文件夹下的mp-weixin
小程序配置

使用常用的UI组件库
1、uview https://www.uviewui.com/
尤其针对底部tabbar动态显示,给出了优化方案,采用还是原生得tabbar
uView2.0重磅发布,利剑出鞘,一统江湖,https://ext.dcloud.net.cn/plugin?id=1593
2、Thor UI组件库 https://thorui.cn/doc/
ThorUI组件库 - DCloud 插件市场,https://ext.dcloud.net.cn/plugin?id=556
3、 GraceUI http://grace.hcoder.net/manual/info/167-110.html
4、FirstUI 组件库 FirstUI(https://www.firstui.cn/)
FirstUI 组件库 - DCloud插件市场,https://ext.dcloud.net.cn/plugin?id=7646
5、vantUi 组件库 https://vant-ui.github.io/vant-weapp/#/home
uview安装和使用
uView依赖SCSS,您必须要安装此插件,否则无法正常运行。
- 如果您的项目是由H
Builder X创建的,相信已经安装scss插件,如果没有,请在HX菜单的 工具->插件安装中找到"scss/sass编译"插件进行安装, 如不生效,重启HX即可 - 如果您的项目是由
vue-cli创建的,请通过以下命令安装对sass(scss)的支持,如果已安装,请略过。
// 安装node-sass
npm i node-sass -D
// 安装sass-loader
npm i sass-loader -D
使用npm安装
初次使用npm安装的话,在项目页面下初始化一下
npm init -y
安装uview
npm install uview-ui@1.8.8
如果
npm下载 npm err network报错的话,就需要修改npm的下载源地址(npm下载默认源是国外地址)
也可使用国内的下载工具cnpm
配置使用
- 引入uView主JS库
在项目根目录中的main.js中,引入并使用uView的JS库,注意这两行要放在import Vue之后。
// main.js
import uView from "uview-ui";
Vue.use(uView);
- 在引入uView的全局SCSS主题文件
在项目根目录的uni.scss中引入此文件。
/* uni.scss */
@import 'uview-ui/theme.scss';
- 引入uView基础样式
注意!
在App.vue中首行的位置引入,注意给style标签加入lang="scss"属性
<style lang="scss">/* 注意要写在第一行,同时给style标签加入lang="scss"属性 */@import "uview-ui/index.scss";
</style>
- 配置easycom组件模式
此配置需要在项目根目录的pages.json中进行。
温馨提示
uni-app为了调试性能的原因,修改easycom规则不会实时生效,配置完后,您需要重启HX或者重新编译项目才能正常使用uView的功能。
请确保您的pages.json中只有一个easycom字段,否则请自行合并多个引入规则。
// pages.json
{"easycom": {"^u-(.*)": "uview-ui/components/u-$1/u-$1.vue"},// 此为本身已有的内容"pages": [// ......]
}
相关文章:

使用uniapp开发小程序(基础篇)
本文章只介绍微信小程序的开发流程,如果需要了解其他平台的开发的流程的话,后续根据情况更新相应的文章,也可以根据uniapp官网的链接了解不同平台的开发流程 HBuilderX使用:https://uniapp.dcloud.net.cn/quickstart-hx.html 开发工具 开始…...

vue3【详解】组合式函数
什么是组合式函数? 利用 Vue 的组合式 API 来封装和复用有状态逻辑的函数,用于实现逻辑复用,类似 react18 中的 hook 函数名称 – 以 use 开头,采用驼峰命名,如 useTitle参数 – 建议使用 toValue() 处理(…...

微服务实战系列之玩转Docker(六)
前言 刚进入大暑,“清凉不肯来,烈日不肯暮”,空调开到晚,还是满身汗。——碎碎念 我们知道,仓库可见于不同领域,比如粮食仓库、数据仓库。在容器领域,自然也有镜像仓库(registry&…...

Python题解Leetcode Hot100之动态规划
动态规划解题步骤-5部曲 确定dp数组(dp table)以及下标的含义确定递推公式dp数组如何初始化确定遍历顺序举例推导dp数组 70. 爬楼梯 题目描述 假设你正在爬楼梯。需要 n 阶你才能到达楼顶。每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到…...

你了解GD32 MCU上下电要求吗
你了解GD32 MCU的上下电要求吗?MCU的上下电对于系统的稳定运行非常重要。 以GD32F30X为例,上电/掉电复位波形如如下图所示。 上电过程中,VDD/VDDA电压上电爬坡,当电压高于VPOR(上电复位电压)MCU开始启动&a…...

二、【Python】入门 - 【PyCharm】安装教程
往期博主文章分享文章: 【机器学习】专栏http://t.csdnimg.cn/sQBvw 目录 第一步:PyCharm下载 第二步:安装(点击安装包打开下图页面) 第三步:科学使用,请前往下载最新工具及教程:…...

2、程序设计语言基础知识
这一章节的内容在我们的软件设计师考试当中,考的题型比较固定,基本都是选择题,分值大概在2~4分左右。 而且考的还多是程序设计语言的一些基本语法,特别是这两年比较火的Python。 所以对于有一定要编程基础的即使本章的内容不学习&…...
:TP-Link联洲)
ARM/Linux嵌入式面经(十八):TP-Link联洲
文章目录 虚拟内存,页表,copy on write面试题1:面试题2:面试题3:进程和线程的区别红黑树和b+树的应用红黑树的应用B+树的应用视频会议用了哪些协议1. H.323协议2. SIP协议(会话发起协议)3. WebRTC(网页实时通信)4. 其他协议io多路复用(select,poll,epoll)面试题li…...

解读vue3源码-响应式篇2
提示:看到我 请让我滚去学习 文章目录 vue3源码剖析reactivereactive使用proxy代理一个对象1.首先我们会走isObject(target)判断,我们reactive全家桶仅对对象类型有效(对象、数组和 Map、Set 这样的集合类型),而对 str…...

【测开能力提升-fastapi框架】fastapi能力提升 - 中间件与CORS
1. 中间件 1.1 介绍(ChatGPT抄的,大致可以理解) 一种机制,用于在处理请求和响应之前对其进行拦截、处理或修改。中间件可以在应用程序的请求处理管道中插入自定义逻辑,以实现一些通用的功能,如身份验证、…...

centos7安装es及简单使用
为了方便日后查看,简单记录下! 【启动es前,需要调整这个配置文件(/opt/elasticsearch-6.3.0/config/elasticsearch.yml)的两处ip地址,同时访问页面地址的ip:9200时,ip地址也对应修改】 【启动kibana前,需要调整这个配置文件(/opt/kibana-6.3.0/config/k…...
)
2024年自动驾驶SLAM面试题及答案(更新中)
自动驾驶中的SLAM(Simultaneous Localization and Mapping,即同步定位与地图构建)是关键技术,它能够让车辆在未知环境中进行自主定位和地图建构。秋招来临之际,相信大家都已经在忙碌的准备当中了,尤其是应届…...
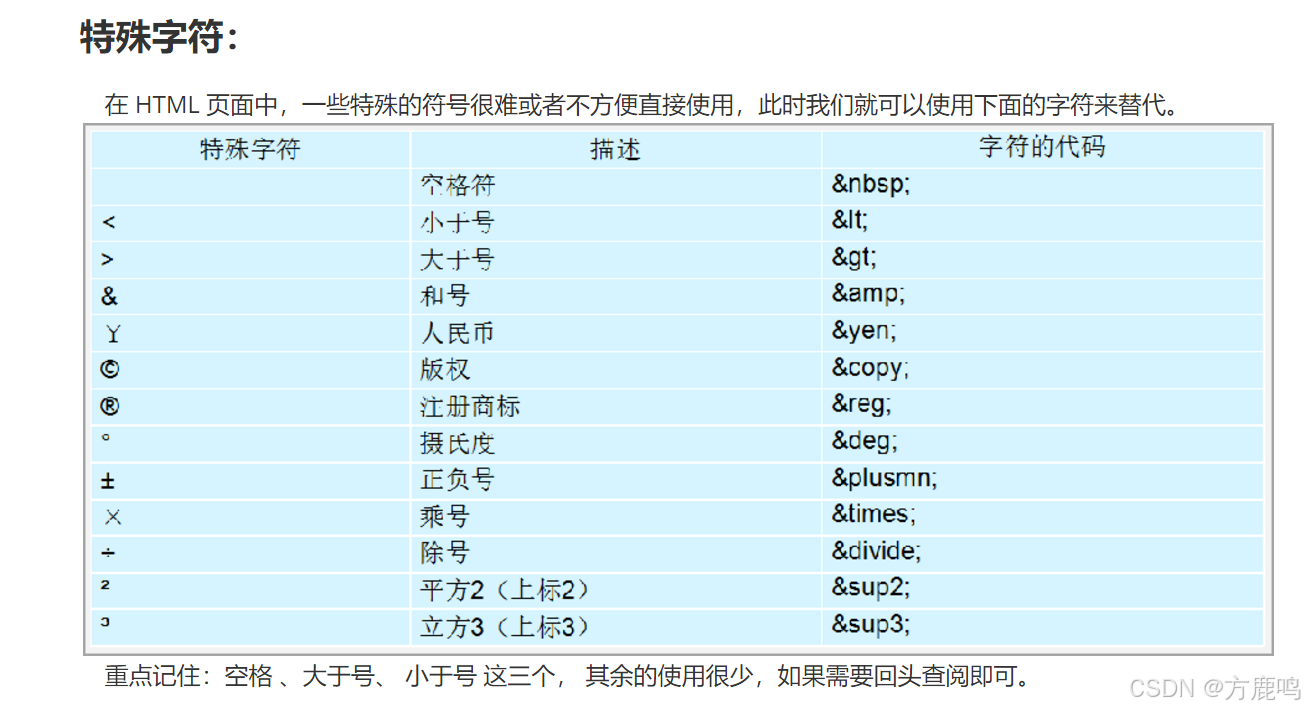
HTML零基础自学笔记(上)-7.18
HTML零基础自学笔记(上) 参考:pink老师一、HTML, Javascript, CSS的关系是什么?二、什么是HTML?1、网页,网站的概念2、THML的基本概念3、THML的骨架标签/基本结构标签 三、HTML标签1、THML标签介绍2、常用标签图像标签ÿ…...

数学建模--图论与最短路径
目录 图论与最短路径问题 最短路径问题定义 常用的最短路径算法 Dijkstra算法 Floyd算法 Bellman-Ford算法 SPFA算法 应用实例 结论 延伸 如何在实际应用中优化Dijkstra算法以提高效率? 数据结构优化: 边的优化: 并行计算&…...

FLINK-checkpoint失败原因及处理方式
在 Flink 或其他分布式数据处理系统中,Checkpoint 失败可能由多种原因引起。以下是一些常见的原因: 资源不足: 如果 TaskManager 的内存或磁盘空间不足,可能无法完成状态的快照,导致 Checkpoint 失败。 网络问题&am…...

Hbase映射为Hive外表
作者:振鹭 Hbase对应Hive外表 (背景:在做数据ETL中,可能原始数据在列式存储Hbase中,这个时候,如果我们想清洗数据,可以考虑把Hbase表映射为Hive的外表,然后使用Hive的HQL来清除处理数据) 1. …...
题解)
洛谷P1002(过河卒)题解
题目传送门 思路 直接爆搜会TLE,所以考虑进行DP。 由于卒只可以从左边和上面走,所以走到(i,j)的路程总数为从上面走的路程总数加上从左边走的路程总数。我们用dp[i][j]表示从起点走到(i,j)的路程总数,那么状态转移方程为: dp[…...

微信小程序 async-validator 表单验证 第三方包
async-validator 是一个基于 JavaScript 的表单验证库,支持异步验证规则和自定义验证规则 主流的 UI 组件库 Ant-design 和 Element 中的表单验证都是基于 async-validator 使用 async-validator 可以方便地 构建表单中逻辑,使得错误提示信息更加友好和灵…...

马克·扎克伯格解释为何开源AI对开发者有利
Meta 今天发布了 Llama 3.1 系列人工智能模型,在人工智能领域取得了重大进展,其性能可与领先的闭源模型相媲美。值得一提的是,在多项人工智能基准测试中,Llama 3.1 405B 模型的性能超过了 OpenAI 的 GPT-4o 和 Claude 3.5 Sonnet。…...

游戏外挂的技术实现与五年脚本开发经验分享
引言: 在数字娱乐的浪潮中,电子游戏成为许多人生活中不可或缺的一部分。然而,随着游戏的普及,一些玩家为了追求更高效的游戏体验或不正当竞争优势,开始使用游戏外挂程序。这些外挂往往通过修改游戏正常运行机制来提供非…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

elementUI点击浏览table所选行数据查看文档
项目场景: table按照要求特定的数据变成按钮可以点击 解决方案: <el-table-columnprop"mlname"label"名称"align"center"width"180"><template slot-scope"scope"><el-buttonv-if&qu…...

【iOS】 Block再学习
iOS Block再学习 文章目录 iOS Block再学习前言Block的三种类型__ NSGlobalBlock____ NSMallocBlock____ NSStackBlock__小结 Block底层分析Block的结构捕获自由变量捕获全局(静态)变量捕获静态变量__block修饰符forwarding指针 Block的copy时机block作为函数返回值将block赋给…...

比特币:固若金汤的数字堡垒与它的四道防线
第一道防线:机密信函——无法破解的哈希加密 将每一笔比特币交易比作一封在堡垒内部传递的机密信函。 解释“哈希”(Hashing)就是一种军事级的加密术(SHA-256),能将信函内容(交易细节…...
