Python题解Leetcode Hot100之动态规划
动态规划解题步骤-5部曲
- 确定dp数组(dp table)以及下标的含义
- 确定递推公式
- dp数组如何初始化
- 确定遍历顺序
- 举例推导dp数组
70. 爬楼梯
题目描述
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶?
解题思路
f(n) = f(n-2) + f(n-1)
Python代码
class Solution:def climbStairs(self, n: int) -> int:n_1 = n_2 = 1if n <=1:return 1for i in range(2, n+1):f_n = n_1 + n_2n_2 = n_1n_1 = f_nreturn f_n
118. 杨辉三角
题目描述
给定一个非负整数 numRows,生成杨辉三角的前 numRows 行。
解题思路
杨辉三角的每个元素是上一行左右两个元素之和,边界元素为 1。用一个二维列表来存储结果,每行第一个和最后一个元素固定为 1,其他元素是它左上和右上的和。
Python代码
class Solution:def generate(self, numRows: int) -> List[List[int]]:if numRows == 0:return []res = [[1]]if numRows == 1:return resres.append([1, 1])if numRows == 2:return resfor i in range(3, numRows+1):last_nums = res[-1] cur_nums = [1]numRows = len(last_nums)for j in range(numRows-1):cur_nums.append(last_nums[j]+last_nums[j+1])cur_nums.append(1)res.append(cur_nums)return res
198. 打家劫舍
题目描述
你是一个专业的窃贼,计划偷窃沿街的房屋。每间房内都藏有一定的现金,如果相邻的两间房屋在同一晚上被小偷闯入,系统会自动报警。给定一个代表每个房屋存放金额的非负整数数组,计算你不触动报警装置的情况下,今晚能够偷窃到的最高金额。
解题思路
使用动态规划来解决。假设 dp[i] 表示前 i 间房屋所能偷窃的最高金额,则状态转移方程为 dp[i] = max(dp[i-1], dp[i-2] + nums[i]),初始条件为 dp[0] = nums[0] 和 dp[1] = max(nums[0], nums[1])。
Python代码
class Solution:def rob(self, nums: List[int]) -> int:n = len(nums)dp = [0]*nif n ==1:return nums[0]dp[0] = nums[0]dp[1] = max(nums[0], nums[1])for i in range(2, n):dp[i] = max(dp[i-1], nums[i]+dp[i-2])return dp[n-1]
279. 完全平方数
题目描述
给你一个整数 n ,返回 和为 n 的完全平方数的最少数量 。
解题思路
使用动态规划来解决。假设 dp[i] 表示组成整数 i 所需要的最少的完全平方数的数量,则状态转移方程为 dp[i] = min(dp[i - 1* 1] + 1,dp[i - 2 * 2] + 1,... , dp[i - j * j] + 1),其中 j * j 是当前平方数,由此来更新每一个 dp 位置。
求和问题
Python代码
class Solution:def numSquares(self, n: int) -> int:dp = [0] * (n + 1)dp[1] = 1for i in range(2, n + 1):j = 1res = float('inf')while j * j <= i:res = min(res, dp[i - j * j] + 1)j += 1dp[i] = resreturn dp[n]
322. 零钱兑换
题目描述
给定不同面额的硬币和一个总金额。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额,返回 -1。
解题思路
完全背包问题:
背包容量:总金额
物品重量:硬币价值
物品价值:数量
假设 dp[i] 表示金额 i 所需的最小硬币数,则状态转移方程为 dp[i] = min(dp[i], dp[i - coin] + 1),其中 coin 是可选的硬币面值。
完全背包的物品可以被取无数次,因此完全背包的内循环为正序,当前物品可以被重复取用;
Python代码
class Solution:def coinChange(self, coins: List[int], amount: int) -> int:n = len(coins)dp = [float("inf")] * (amount + 1)dp[0] = 0for i in range(1, amount + 1):if i % coins[0] == 0:dp[i] = i // coins[0]for i in range(1, n):for j in range(coins[i], amount + 1):dp[j] = min(dp[j], dp[j-coins[i]] + 1)return -1 if dp[amount] == float("inf") else dp[amount]
139. 单词拆分
题目描述
给定一个非空字符串 s 和一个包含非空单词列表的字典 wordDict,判定 s 是否可以被空格拆分为一个或多个在字典中出现的单词。
输入: s = “applepenapple”, wordDict = [“apple”, “pen”]
输出: true
解题思路
可以转化成完全背包问题,而且是排列问题,字符串s是背包,字符串列表里的字符是物品; dp[i] 表示前 i 个字符是否能被拆分; 因为是排列问题,所以外循环遍历背包,内循环遍历物品;
Python代码
class Solution:def wordBreak(self, s: str, wordDict: List[str]) -> bool:n = len(s)word_n = len(wordDict)dp = [False] * (n + 1)dp[0] = Truefor j in range(1, n+1):for i in range(word_n):if j >= len(wordDict[i]):dp[j] = (dp[j] or (s[j - len(wordDict[i]):j] == wordDict[i] and dp[j-len(wordDict[i])]))# print(dp)return dp[n]
300. 最长递增子序列
题目描述
给定一个无序的整数数组,找到其中最长递增子序列的长度。
解题思路
使用动态规划来解决。假设 dp[i] 表示以 nums[i] 结尾的最长递增子序列的长度,则状态转移方程为:dp[i] = max(dp[j] + 1),其中 j 从 0 到 i-1 且 nums[j] < nums[i]。
Python代码
class Solution:def lengthOfLIS(self, nums: List[int]) -> int:n = len(nums)dp = [1] * nres = 1for i in range(1, n):for j in range(i):if nums[j] < nums[i]:dp[i] = max(dp[i], dp[j] + 1)res = max(res, dp[i])return res
152. 乘积最大子数组
题目描述
给你一个整数数组 nums ,请你找出数组中乘积最大的连续子数组(该子数组中至少包含一个数字),并返回该子数组所对应的乘积。
输入: nums = [2,3,-2,4]
输出: 6
解释: 子数组 [2,3] 有最大乘积 6。
解题思路
使用动态规划来解决。维护两个变量 max_val 和 min_val,表示以当前元素为结尾的子数组的最大乘积和最小乘积,然后遍历数组更新这两个值。
Python代码
class Solution:def maxProduct(self, nums: List[int]) -> int:if not nums:return 0max_val = min_val = res = nums[0]for i in range(1, len(nums)):if nums[i] < 0:max_val, min_val = min_val, max_valmax_val = max(nums[i], max_val * nums[i])min_val = min(nums[i], min_val * nums[i])res = max(res, max_val)return res
416. 分割等和子集
题目描述
给定一个只包含正整数的非空数组,判断是否可以将这些数字分成两个子集,使得两个子集的元素和相等。
解题思路
转换0,1背包问题,判断是否能找到一个子集,其和等于总和的一半。01背包问题,内循环反向遍历
Python代码
class Solution:def canPartition(self, nums: List[int]) -> bool:n = len(nums)s = sum(nums)if s % 2 != 0:return Falsetarget = s // 2dp = [False] * (target + 1)dp[0] = Truefor i in range(1, target + 1):if nums[0] == i:dp[i] = Truefor i in range(1, n):# 0,1背包,反向遍历for j in range(target, nums[i] - 1, -1):dp[j] = dp[j] or dp[j - nums[i]]return dp[target]
32. 最长有效括号
题目描述
给定一个只包含 ‘(’ 和 ‘)’ 的字符串,找出最长有效(格式正确且连续)括号子串的长度。
解题思路
使用动态规划来解决。假设 dp[i] 表示以 i 结尾的最长有效括号的长度。状态转移方程根据当前字符和前一个字符的情况来判断。如果s[i]=‘(’,那么dp[i]一定是0, s[i] ='('的情况见代码中的注释。
Python代码
class Solution:# ((()))# 012345def longestValidParentheses(self, s: str) -> int:n =len(s)dp = [0] * nres = 0for i in range(1, n):if s[i] == '(':continue# 当前是')', 前一个字符是'('if s[i - 1] == '(':if i == 1:dp[i] = 2else:dp[i] = dp[i-2] + 2# 当前是')', 前一个也是')',那就需要判断s[i - 1 - dp[i-1]]是不是'(',是的话就能和当前的')'匹配上elif i - 1 - dp[i-1] >= 0 and s[i - 1 - dp[i-1]] == '(':dp[i] = dp[i-1] + 2if i - 2 - dp[i-1] >= 0:dp[i] += dp[i - 2 - dp[i-1]]res = max(res, dp[i])return res
相关文章:

Python题解Leetcode Hot100之动态规划
动态规划解题步骤-5部曲 确定dp数组(dp table)以及下标的含义确定递推公式dp数组如何初始化确定遍历顺序举例推导dp数组 70. 爬楼梯 题目描述 假设你正在爬楼梯。需要 n 阶你才能到达楼顶。每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到…...

你了解GD32 MCU上下电要求吗
你了解GD32 MCU的上下电要求吗?MCU的上下电对于系统的稳定运行非常重要。 以GD32F30X为例,上电/掉电复位波形如如下图所示。 上电过程中,VDD/VDDA电压上电爬坡,当电压高于VPOR(上电复位电压)MCU开始启动&a…...

二、【Python】入门 - 【PyCharm】安装教程
往期博主文章分享文章: 【机器学习】专栏http://t.csdnimg.cn/sQBvw 目录 第一步:PyCharm下载 第二步:安装(点击安装包打开下图页面) 第三步:科学使用,请前往下载最新工具及教程:…...

2、程序设计语言基础知识
这一章节的内容在我们的软件设计师考试当中,考的题型比较固定,基本都是选择题,分值大概在2~4分左右。 而且考的还多是程序设计语言的一些基本语法,特别是这两年比较火的Python。 所以对于有一定要编程基础的即使本章的内容不学习&…...
:TP-Link联洲)
ARM/Linux嵌入式面经(十八):TP-Link联洲
文章目录 虚拟内存,页表,copy on write面试题1:面试题2:面试题3:进程和线程的区别红黑树和b+树的应用红黑树的应用B+树的应用视频会议用了哪些协议1. H.323协议2. SIP协议(会话发起协议)3. WebRTC(网页实时通信)4. 其他协议io多路复用(select,poll,epoll)面试题li…...

解读vue3源码-响应式篇2
提示:看到我 请让我滚去学习 文章目录 vue3源码剖析reactivereactive使用proxy代理一个对象1.首先我们会走isObject(target)判断,我们reactive全家桶仅对对象类型有效(对象、数组和 Map、Set 这样的集合类型),而对 str…...

【测开能力提升-fastapi框架】fastapi能力提升 - 中间件与CORS
1. 中间件 1.1 介绍(ChatGPT抄的,大致可以理解) 一种机制,用于在处理请求和响应之前对其进行拦截、处理或修改。中间件可以在应用程序的请求处理管道中插入自定义逻辑,以实现一些通用的功能,如身份验证、…...

centos7安装es及简单使用
为了方便日后查看,简单记录下! 【启动es前,需要调整这个配置文件(/opt/elasticsearch-6.3.0/config/elasticsearch.yml)的两处ip地址,同时访问页面地址的ip:9200时,ip地址也对应修改】 【启动kibana前,需要调整这个配置文件(/opt/kibana-6.3.0/config/k…...
)
2024年自动驾驶SLAM面试题及答案(更新中)
自动驾驶中的SLAM(Simultaneous Localization and Mapping,即同步定位与地图构建)是关键技术,它能够让车辆在未知环境中进行自主定位和地图建构。秋招来临之际,相信大家都已经在忙碌的准备当中了,尤其是应届…...
HTML零基础自学笔记(上)-7.18
HTML零基础自学笔记(上) 参考:pink老师一、HTML, Javascript, CSS的关系是什么?二、什么是HTML?1、网页,网站的概念2、THML的基本概念3、THML的骨架标签/基本结构标签 三、HTML标签1、THML标签介绍2、常用标签图像标签ÿ…...

数学建模--图论与最短路径
目录 图论与最短路径问题 最短路径问题定义 常用的最短路径算法 Dijkstra算法 Floyd算法 Bellman-Ford算法 SPFA算法 应用实例 结论 延伸 如何在实际应用中优化Dijkstra算法以提高效率? 数据结构优化: 边的优化: 并行计算&…...

FLINK-checkpoint失败原因及处理方式
在 Flink 或其他分布式数据处理系统中,Checkpoint 失败可能由多种原因引起。以下是一些常见的原因: 资源不足: 如果 TaskManager 的内存或磁盘空间不足,可能无法完成状态的快照,导致 Checkpoint 失败。 网络问题&am…...

Hbase映射为Hive外表
作者:振鹭 Hbase对应Hive外表 (背景:在做数据ETL中,可能原始数据在列式存储Hbase中,这个时候,如果我们想清洗数据,可以考虑把Hbase表映射为Hive的外表,然后使用Hive的HQL来清除处理数据) 1. …...
题解)
洛谷P1002(过河卒)题解
题目传送门 思路 直接爆搜会TLE,所以考虑进行DP。 由于卒只可以从左边和上面走,所以走到(i,j)的路程总数为从上面走的路程总数加上从左边走的路程总数。我们用dp[i][j]表示从起点走到(i,j)的路程总数,那么状态转移方程为: dp[…...

微信小程序 async-validator 表单验证 第三方包
async-validator 是一个基于 JavaScript 的表单验证库,支持异步验证规则和自定义验证规则 主流的 UI 组件库 Ant-design 和 Element 中的表单验证都是基于 async-validator 使用 async-validator 可以方便地 构建表单中逻辑,使得错误提示信息更加友好和灵…...

马克·扎克伯格解释为何开源AI对开发者有利
Meta 今天发布了 Llama 3.1 系列人工智能模型,在人工智能领域取得了重大进展,其性能可与领先的闭源模型相媲美。值得一提的是,在多项人工智能基准测试中,Llama 3.1 405B 模型的性能超过了 OpenAI 的 GPT-4o 和 Claude 3.5 Sonnet。…...

游戏外挂的技术实现与五年脚本开发经验分享
引言: 在数字娱乐的浪潮中,电子游戏成为许多人生活中不可或缺的一部分。然而,随着游戏的普及,一些玩家为了追求更高效的游戏体验或不正当竞争优势,开始使用游戏外挂程序。这些外挂往往通过修改游戏正常运行机制来提供非…...
认识神经网络【多层感知器数学原理】
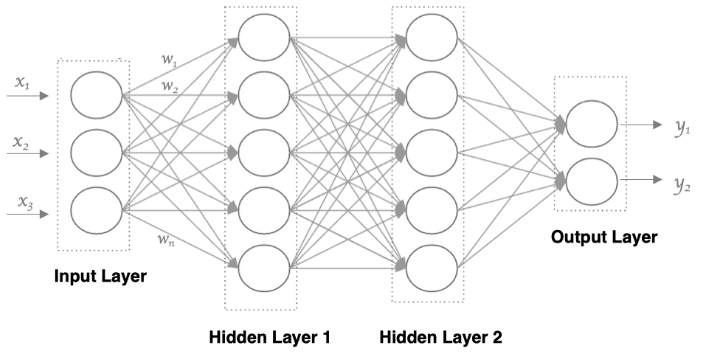
文章目录 1、什么是神经网络2、人工神经网络3、多层感知器3.1、输入层3.2、隐藏层3.2.1、隐藏层 13.2.2、隐藏层 2 3.3、输出层3.4、前向传播3.4.1、加权和⭐3.4.2、激活函数 3.5、反向传播3.5.1、计算梯度3.5.2、更新权重和偏置 4、小结 🍃作者介绍:双非…...

MySQL入门学习-SQL高级技巧.CTE和递归查询
在 MySQL 中,SQL 高级技巧包括了 Common Table Expressions(CTE)和递归查询等。 一、CTE(Common Table Expressions,公共表表达式)的概念: CTE 是一个临时的结果集,它可以在一个查询…...

键盘是如何使用中断机制的?当打印一串字符到显示屏上时发生了什么???
当在键盘上按下一个键时会进行一下操作: 1.当按下任意一个键时,键盘编码器监控会来判断按下的键是哪个 2.键盘控制器用将解码,将键盘的数据保存到键盘控制器里数据寄存器里面 3.此时发送一个中断请求给中断控制器,中断控制器获取到中断号发送…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...

python爬虫——气象数据爬取
一、导入库与全局配置 python 运行 import json import datetime import time import requests from sqlalchemy import create_engine import csv import pandas as pd作用: 引入数据解析、网络请求、时间处理、数据库操作等所需库。requests:发送 …...
