题解:T480718 eating
eating
题目背景
从前有个荣光的王国,小 A 是里面的国王,今天他要赐予他的子民以仓廪。
题目描述
在一条街上有 n n n 个饭店。小 A 站在这条街的最左端。
第 i i i 个饭店离这条街最左端的距离是 a i a_i ai,它所售卖的菜品的美味值是 b i b_i bi。
小 A 不想走太多路,但是又想吃到好吃的东西。因此他定义一个饭店的吸引力是 w i = b i a i w_i = \frac{b_i}{a_i} wi=aibi。
小 A 想知道吸引力最大的饭店的编号是多少。如果有多个吸引力最大的饭店,你要告诉他距离街道左端距离最近的那个饭店的编号。
输入格式
第一行是一个整数 n n n,表示商店的个数。
接下来 n n n 行,每行两个整数,表示一个商店离街道左端的距离 a i a_i ai 个菜品美味值 b i b_i bi。
输出格式
输出一行一个整数,表示答案。
样例 #1
样例输入 #1
3
1 2
2 4
3 9
样例输出 #1
3
样例 #2
样例输入 #2
3
1 2
2 3
3 4
样例输出 #2
1
样例 #3
样例输入 #3
3
1 1
2 3
4 6
样例输出 #3
2
提示
数据规模与约定
- 对 20 % 20\% 20% 的数据, n = 2 n = 2 n=2。
- 对 40 % 40\% 40% 的数据,保证 b i b_i bi 是 a i a_i ai 的倍数。
- 对 60 % 60\% 60% 的数据,保证给出的 a i a_i ai 单调递增。
- 对 80 % 80\% 80% 的数据,保证 n ≤ 1000 n \leq 1000 n≤1000。
- 对 100 % 100\% 100% 的数据,保证 2 ≤ n ≤ 1 0 5 2 \leq n \leq 10^5 2≤n≤105, 1 ≤ a i , b i ≤ 1 0 9 1 \leq a_i, b_i \leq 10^9 1≤ai,bi≤109, a i a_i ai 互不相同。
为了解决这个问题,我们可以遍历所有的饭店,计算每个饭店的吸引力 w i = b i a i w_i = \frac{b_i}{a_i} wi=aibi,并记录当前最大的吸引力和对应的饭店编号。如果有多个饭店的吸引力相同且都是最大的,我们还需要记录这些饭店中距离街道左端最近的饭店编号。
以下是具体的Python代码实现:
n = int(input().strip()) # 读取饭店数量
max_attraction = float('-inf') # 初始化最大吸引力为负无穷
closest_restaurant = 0 # 初始化距离街道左端最近的饭店编号为0(实际上这个初始值不会被使用)
answer = 0 # 初始化答案为0(实际答案会在这个基础上更新)for i in range(n):a_i, b_i = map(int, input().strip().split()) # 读取每个饭店的距离和美味值w_i = b_i / a_i # 计算吸引力# 如果当前饭店的吸引力大于已知的最大吸引力if w_i > max_attraction:max_attraction = w_i # 更新最大吸引力answer = i + 1 # 更新答案为当前饭店的编号# 如果当前饭店的吸引力等于已知的最大吸引力,但距离更近elif w_i == max_attraction and a_i < min(a_i for _, a_i in enumerate(range(answer-1, -1, -1))):# 注意这里我们假设answer-1之前的饭店的a_i都已经被读取过了,但实际上我们需要一个额外的数据结构来存储这些值# 但由于题目保证a_i互不相同,我们可以直接更新answer,因为更近的饭店一定在更前面被读取answer = i + 1 # 更新答案为当前饭店的编号print(answer) # 输出答案
然而,上面的代码在处理距离更近的饭店时存在逻辑上的不严谨,因为我们在遍历过程中并没有存储之前所有饭店的距离。但由于题目保证 a i a_i ai 互不相同,我们可以简化处理:当遇到吸引力相同的饭店时,我们直接更新答案,因为后读取的饭店(即距离更近的)会覆盖之前的答案。
下面是简化后的代码:
n = int(input().strip())
max_attraction = float('-inf')
answer = 0for i in range(n):a_i, b_i = map(int, input().strip().split())w_i = b_i / a_iif w_i > max_attraction or (w_i == max_attraction and i + 1 < answer):max_attraction = w_ianswer = i + 1print(answer)
这样,我们就可以正确地找到吸引力最大且距离街道左端最近的饭店编号了。
相关文章:

题解:T480718 eating
eating 题目背景 从前有个荣光的王国,小 A 是里面的国王,今天他要赐予他的子民以仓廪。 题目描述 在一条街上有 n n n 个饭店。小 A 站在这条街的最左端。 第 i i i 个饭店离这条街最左端的距离是 a i a_i ai,它所售卖的菜品的美味…...

MATLAB中matfile用法
目录 语法 说明 示例 创建 MAT 文件对象 启用对 MAT 文件的写访问权限 加载整个变量 将整个变量保存至现有 MAT 文件 加载和保存部分变量 确定变量大小 参数说明 局限性 提示 matfile的功能是访问和更改 MAT 文件中的变量,而不必将文件加载到内存中。 …...

Spring之Spring Bean的生命周期
Spring Bean的生命周期 通过BeanDefinition获取bean的定义信息调用构造函数实例化beanBean的依赖注入处理Aware接口(BeanNameAware、BeanFactoryAware、ApplicationContextAware)Bean的后置处理器BeanPostProcessor-前置初始化方法(Initiali…...

OSINT 开源情报中的地理定位方法
了解 OSINT 中的地理定位技术、如何获取地理位置数据以及如何将地理定位用于各种调查场景。 OSINT 中的地理定位基础知识 OSINT 代表开源情报,指的是从免费公共来源合法收集的有关个人或组织的信息。这包括在互联网上以及书籍、公共图书馆报告、报纸文章、新闻稿、…...

Java面试题系列 - 第17天
Java中的代理模式与动态代理 背景说明:代理模式是一种结构型设计模式,用于在客户端和目标对象之间提供一个代理或占位符。在Java中,动态代理技术允许在运行时创建代理对象,这在AOP(面向切面编程)和RPC&…...

开发环境搭建
1、Ubuntu 系统设置 root 用户密码 新安装的ubuntu没有设置 root 用户密码,打开终端,输入 sudo passwd root 执行命令后依次输入密码 2、虚拟机设置网络适配器 3、Ubuntu 系统下搭建 FTP 服务器 sudo apt-get update sudo apt-get install vsftpd sudo apt-get install vim…...

【NLP】关于参数do_sample的解释
在自然语言处理(NLP)领域,特别是在使用神经网络模型进行文本生成时,do_sample是一个常见的参数,用于控制模型生成文本的方式。具体来说,do_sample参数决定模型是否采用随机采样(sampling&#x…...

Vbox虚拟机+Ubuntu motest测试drm
1. 效果演示 大家做学习drm的时候,没有硬件测试平台不方便测试,这里给大家演示下如何基于Vbox虚拟机Ubuntu测试drm的一些功能,先看下演示视频。 没有光标测试: demo_vwmfgx_test_drm 带有光标测试: demo_vwmfgx_drm_with_cursor 可以看到,有…...
几何 15 转换)
ArcGIS Pro SDK (九)几何 15 转换
ArcGIS Pro SDK (九)几何 15 转换 文章目录 ArcGIS Pro SDK (九)几何 15 转换1 创建地理转换2 创建复合地理变换3 创建投影转换4 创建高压基准变换5 创建复合高压基准变换6 决定转换7 地图点 - 地理坐标字符串转换 环境࿱…...

Spring IOC DI --- 认识IOC DI
T04BF 👋专栏: 算法|JAVA|MySQL|C语言 🫵 今天你敲代码了吗 文章目录 认识Ioc & DIIoc是什么?DI是什么? 认识Ioc & DI 我们知道,Spring 是一个开源框架,让我们的开发更加简单.但是更加具体来说,实际上Spring 是包含了众多工具方法的Ioc容器 …...

常用的python程序汇总——入门级
只用于记录最近的一些日常程序。 目录 前言 一、文件和目录管理 1.读取文件结构 读取所有文件夹和文件 读取到N级子文件夹和文件 只读取到N级子文件夹 2.遍历文件并处理(复制、删除) 说明: 二、数据分析和处理 三、数据可视化 四、…...
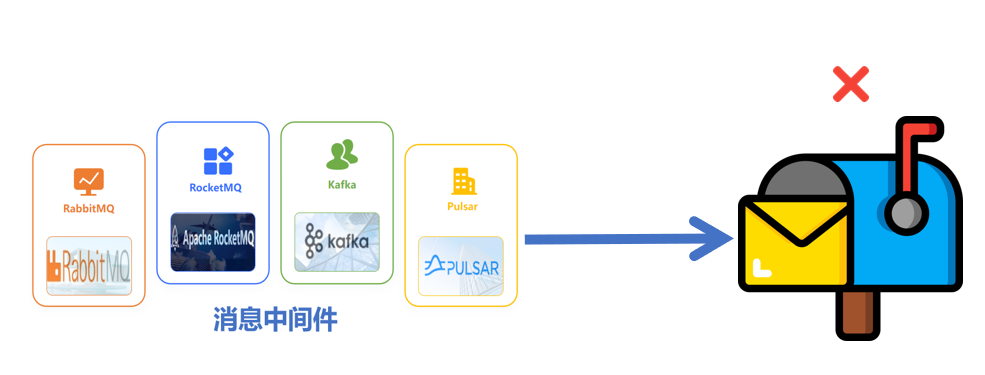
被问到MQ消息已丢失,该如何处理?
在分布式系统中,消息中间件(如 RabbitMQ、RocketMQ、Kafka、Pulsar 等)扮演着关键角色,用于解耦生产者和消费者,并确保数据传输的可靠性和顺序性。尽管我们通常会采取多种措施来防止消息丢失,如消息持久化、…...
)
open3d:ransac分割多个平面(源码)
1、背景介绍 随机采样一致性算法(RANSAC Random Sample Consensus)是一种迭代的参数估计算法,主要用于从包含大量噪声数据的样本中估计模型参数。其核心思想是通过随机采样和模型验证来找到数据中最符合模型假设的点。因此,只要事先给定要提取的参数模型,即可从点云中分割…...
Github 2024-07-17 开源项目日报 Top10
根据Github Trendings的统计,今日(2024-07-17统计)共有10个项目上榜。根据开发语言中项目的数量,汇总情况如下: 开发语言项目数量非开发语言项目3Python项目3Rust项目2TypeScript项目2MDX项目1项目化学习 创建周期:2538 天协议类型:MIT LicenseStar数量:161973 个Fork数量…...

vue3中Composition API写法 <script setup>标签中哪些可以不用导入即可使用?
在 Vue 3 中使用 <script setup> 时,确实有一些全局的 API 和宏可以直接使用,而不需要显式地从 vue 包中导入它们。这是因为 <script setup> 是专门为了提供更简洁的组件编写方式而设计的,它内部利用了编译时的语法糖。 以下是在…...

Facebook Dating:社交平台的约会新体验
随着社交媒体的普及和技术的发展,传统的社交方式正在经历革新,尤其是在约会这个领域。Facebook作为全球领先的社交平台,推出了Facebook Dating,旨在为用户提供一个全新的约会体验。本文将探讨Facebook Dating如何重新定义社交平台…...

【系统架构设计 每日一问】五 搜索型业务,采用MySQL+ES,如何保证数据一致性
将数据从MySQL同步到Elasticsearch(ES)中并保证一致性是一个常见的需求,特别是在需要快速全文搜索和分析功能的应用中。以下是一些常见的方法和实践来确保数据一致性: 1. 使用双写策略 描述:在应用程序层面ÿ…...
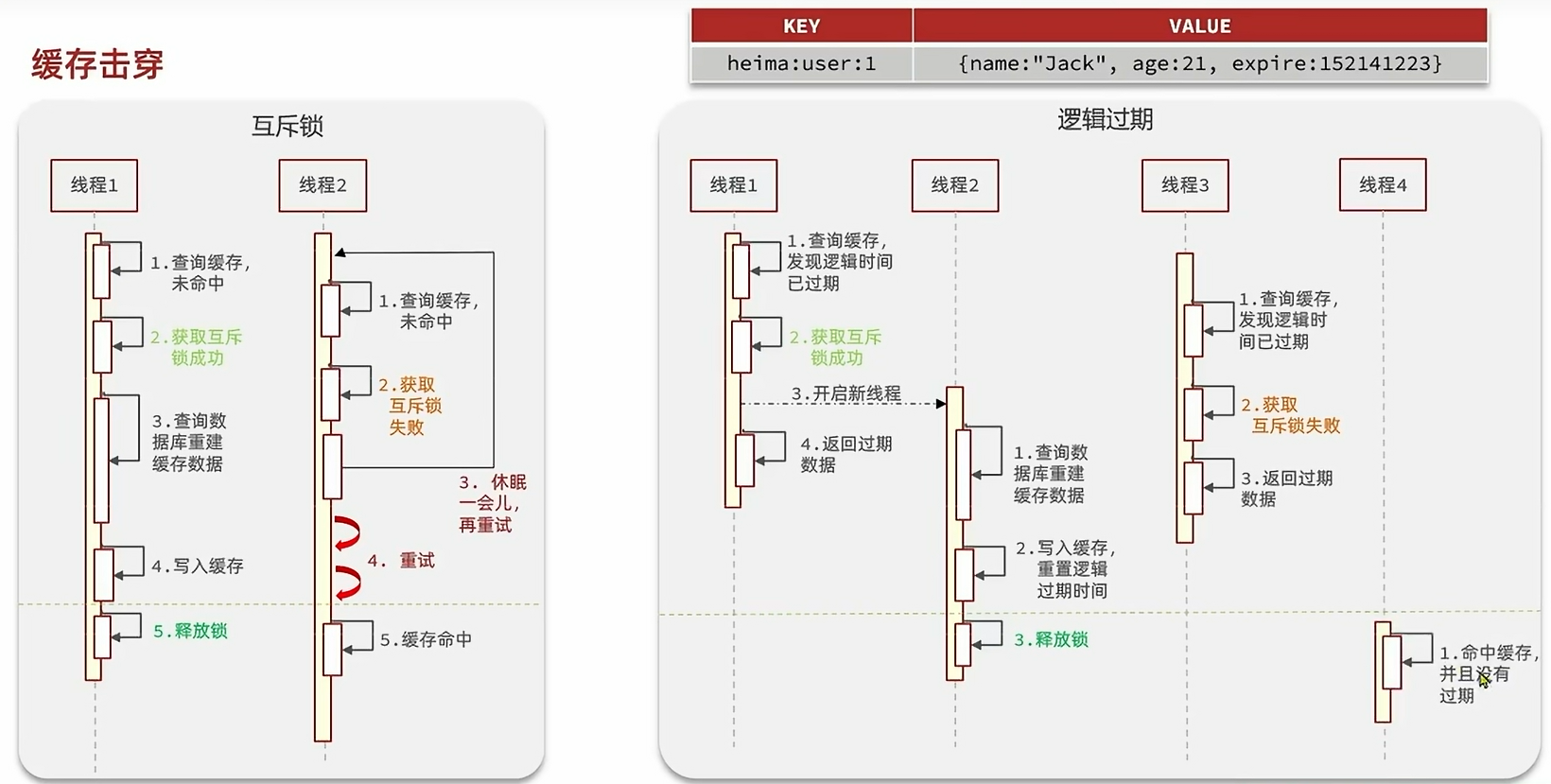
缓存穿透,缓存击穿,缓存雪崩
目录 介绍 缓存穿透 缓存击穿 缓存雪崩 原因 影响 解决方案 缓存穿透 防止缓存穿透->空值缓存案例 缓存击穿 使用互斥锁解决缓存击穿 介绍 缓存穿透 定义:缓存穿透是指用户查询数据,缓存和数据库中都不存在该数据(一般是发起恶意…...

运维 | 清理 Linux 磁盘空间方法汇总
清理 Linux 磁盘空间方法汇总 前言 系统磁盘不够用或占满了,导致部分应用或程序无法正常使用。 本章节将记录一些常用或常见的方法清理系统磁盘(持续更新中)。 常见操作 查看磁盘使用情况 cd / df -Th查找大文件和目录(根目…...

googleTest 源码主线框架性分析——TDD 01
TDD,测试驱动开发,英文全称Test-Driven Development,简称TDD,是一种不同于传统软件开发流程的新型的开发方法。它要求在编写某个功能的代码之前先编写测试代码,然后只编写使测试通过的功能代码,通过测试来推…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...
