react-native从入门到实战系列教程一环境安装篇
充分阅读官网的环境配置指南，严格按照他的指导作业，不然你一直只能在web或沙箱环境下玩玩
极快的网络和科学上网，必备其中的一个- 较好的心理忍受能力，因为上面一点就可以让你放弃
- 坚持不懈，努力尝试
成功效果
三大件
- 开发工具，as(andriod studio) 官网下载，免费使用
- avd手机模拟器，也可以真机看自己选择
- JDK，至少17版本
vdm就是配置模拟器的，按官网的选择版本
sdk的配置,最好不要放在c盘，很吃内存，可以瞬间就让你的c盘爆红，经验之一
系统全局环境配置，因为后面在cmd中会用到android的命令，所以要配置下
设置变量名
path里面进行配置，最下面那行
创建项目
npx react-native@latest init AwesomeProject
编译并运行 React Native 应用
- 确保你先运行了模拟器或者连接了真机，然后在你的项目目录中运行yarn android或者yarn react-native run-android：
cd AwesomeProject
yarn android
# 或者
yarn react-native run-android
可能会经过漫长的等待，会在命令行下载很多东西，切记要忍，还有会奇奇怪怪的错，要会排错！！
然后弹出这个界面，说明你的app已经真正的运行成功了！！！
这里有个https://services.gradle.org/distributions/资源包的下载链接，可以参考下
果不其然！！！cgs！！！下面就可以愉快的玩耍了
切记：多尝试几遍，我也是试了好几次，没有科学上网，全靠网速争气！！不要轻易放弃
相关文章：
react-native从入门到实战系列教程一环境安装篇
充分阅读官网的环境配置指南，严格按照他的指导作业，不然你一直只能在web或沙箱环境下玩玩 极快的网络和科学上网，必备其中的一个较好的心理忍受能力，因为上面一点就可以让你放弃坚持不懈，努力尝试 成功效果 三大件 …...
【Gin】精准应用：Gin框架中工厂模式的现代软件开发策略与实施技巧(下)
【Gin】精准应用：Gin框架中工厂模式的现代软件开发策略与实施技巧(下) 大家好 我是寸铁👊 【Gin】精准应用：Gin框架中工厂模式的现代软件开发策略与实施技巧(下)✨ 喜欢的小伙伴可以点点关注 💝 前言 本次文章分为上下两部分&…...
国科大作业考试资料-人工智能原理与算法-2024新编-第十二次作业整理
袋子里面有3个有偏差的硬币a、b和c，抛掷硬币正面朝上的概率分别是20%、60%和80%。从袋子里随机取出一个硬币（3个硬币被取出的概率是相等的），并把取出的硬币抛掷3次，得到抛掷结果依次是X1 , X2和 X3。 a. 画出对应的贝叶斯网络并定义必要的CPT表。 b. 如果抛掷结果是2次正…...
《0基础》学习Python——第二十一讲__网络爬虫/＜4＞爬取豆瓣电影电影信息
爬取网页数据（获取网页信息全过程） 1、爬取豆瓣电影的电影名称、导演、主演、年份、国家、评价 2、首先我们先爬取页面然后再获取信息 1、爬取网页源码 import requests from lxml import etree if __name__ __main__:#UA伪装head{User-Agent:Mozilla/…...
【C++初阶】string类
【C初阶】string类 🥕个人主页：开敲🍉 🔥所属专栏：C🥭 🌼文章目录🌼 1. 为什么学习string类？ 1.1 C语言中的字符串 1.2 实际中 2. 标准库中的string类 2.1 string类 2.…...
RAS--APEI 报错解析流程(2)
RAS--APEI 报错解析流程(1) 除了APEI 中除了GHES会记录错误，在Post过程中的错误通常是通过BERT Table汇报 1.BERT Boot Error Record Table is used to report unhandled errors that occurred in a previous boot，it is reported as a ‘one-time polle…...
微软蓝屏事件对企业数字化转型有什么影响？
引言：从北京时间2024年7月19日（周五）下午2点多开始，全球大量Windows用户出现电脑崩溃、蓝屏死机、无法重启等情况。事发后，网络安全公司CrowdStrike称，收到大量关于Windows电脑出现蓝屏报告，公司…...
【Gin】精准应用：Gin框架中工厂模式的现代软件开发策略与实施技巧(上)
【Gin】精准应用：Gin框架中工厂模式的现代软件开发策略与实施技巧(上) 大家好 我是寸铁👊 【Gin】精准应用：Gin框架中工厂模式的现代软件开发策略与实施技巧(上)✨ 喜欢的小伙伴可以点点关注 💝 前言 本次文章分为上下两部分&…...
浅谈Devops
1.什么是Devops DevopsDev（Development）Ops（Operation） DevOps（Development和Operations的混合词）是一种重视“软件开发人员（Dev）”和“IT运维技术人员（Ops）”…...
大文件分片上传（前端TS实现）
大文件分片上传 内容 一般情况下，前端上传文件就是new FormData,然后把文件 append 进去，然后post发送给后端就完事了，但是文件越大，上传的文件也就越长，如果在上传过程中，突然网络故障，又或者…...
unity2D游戏开发02添加组件移动玩家
添加组件 给PlayGame和EnemyObject添加组件BoxCollider 2D碰撞器，不用修改参数 给PlayGame添加组件Rigibody 2D 设置数据 添加EnemyObject，属性如下 Edit->project setting->Physics 2D 将 y的值改为0 给playerObject添加标签 新建层 将PlayerObj…...
设计模式 之 —— 单例模式
目录 什么是单例模式？ 定义 单例模式的主要特点 单例模式的几种设计模式 1.懒汉式：线程不安全 2.懒汉式：线程安全 3.饿汉式 4.双重校验锁 单例模式的优缺点 优点： 缺点： 适用场景： 什么是单例模…...
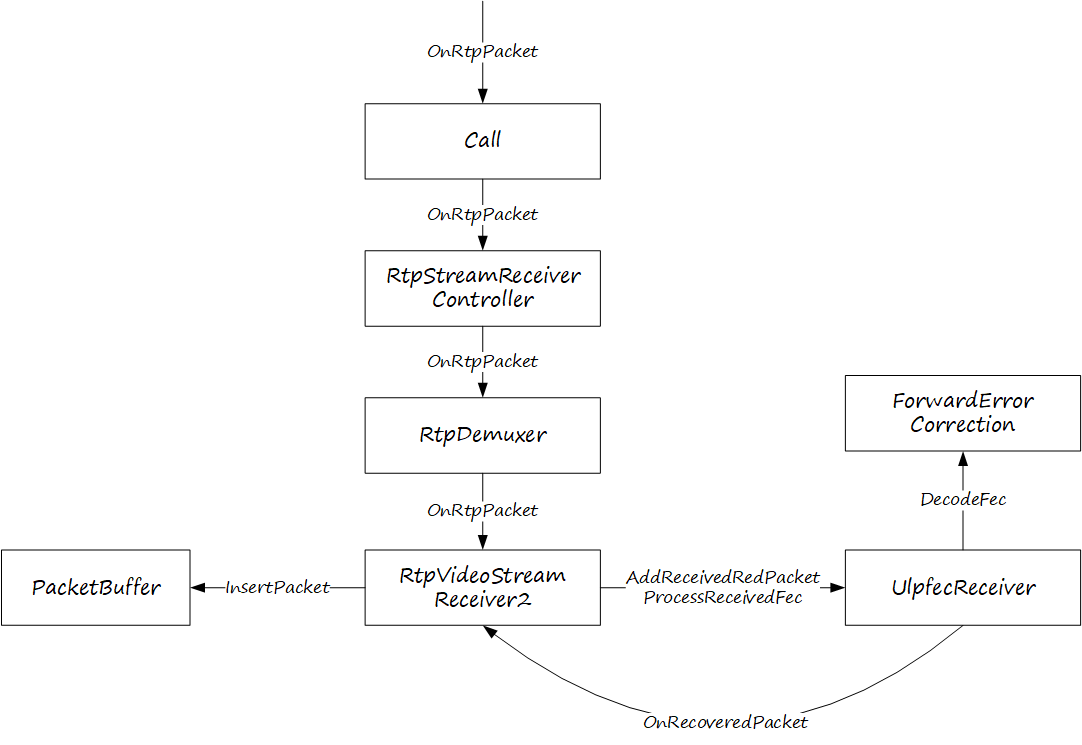
深入浅出WebRTC—ULPFEC
FEC 通过在发送端添加额外的冗余信息，使接收端即使在部分数据包丢失的情况下也能恢复原始数据，从而减轻网络丢包的影响。在 WebRTC 中，FEC 主要有两种实现方式：ULPFEC 和 FlexFEC，FlexFEC 是 ULPFEC 的扩展和升级&…...
Python从0到100（四十三）：数据库与Django ORM 精讲
前言： 零基础学Python：Python从0到100最新最全教程。 想做这件事情很久了，这次我更新了自己所写过的所有博客，汇集成了Python从0到100，共一百节课，帮助大家一个月时间里从零基础到学习Python基础语法、Pyth…...
Redis-主从模式
目录 前言 一.主从节点介绍 二.配置redis主从结构 二.主从复制 四.拓扑结构 五.数据同步 全量复制（Full Sync Replication） 局部复制（Partial Replication） Redis的学习专栏：http://t.csdnimg.cn/a8cvV 前言 …...
加速决策过程：企业级爬虫平台的实时数据分析
摘要 在当今数据驱动的商业环境中，企业如何才能在海量信息中迅速做出精准决策？本文将探讨企业级爬虫平台如何通过实时数据分析加速决策过程，实现数据到决策的无缝衔接。我们聚焦于技术如何赋能企业，提升数据处理效率，…...
字典树（前缀树）数组实现（只能查26个单词）
这段代码实现了一个基于 Trie 树的字典树（Trie）数据结构，用于存储和检索字符串。其中包含以下几个方法. insert(String word): 向 Trie 树中插入一个单词。首先将单词转换为字符数组，然后遍历字符数组，逐个字符在 Trie…...
CTF-pwn-虚拟化-vmmware 前置
文章目录 参考vmware逃逸简介虚拟机和主机通信机制(guest to host)共享内存（弃用）backdoor机制Message_Send和Message_RecvGuestRPC实例RpcOutSendOneRawWork实例 vmware-rpctool info-get guestinfo.ip各个步骤对应的backdoor操作Open RPC channelSend …...
thinkphp8结合layui2.9 图片上传验证
<?php declare (strict_types 1);namespace app\index\validate;use think\Validate;class Upload extends Validate {/*** 定义验证规则* 格式：字段名 > [规则1,规则2...]** var array*/protected $rule [image > fileExt:jpg,png|fileSize:204800|fi…...
农村污水处理难题：探索低成本高效解决方案
农村污水处理难题：探索低成本高效解决方案 农村污水处理作为国家生态文明建设的重要一环，面临着诸多挑战，尤其是技术落后、管理分散、资源匮乏等问题。物联网技术的引入，为解决这些痛点提供了创新途径，实现了对污水处…...
＜6＞-MySQL表的增删查改
目录 一，create（创建表） 二，retrieve（查询表） 1，select列 2，where条件 三，update（更新表） 四，delete（删除表…...
黑马Mybatis
Mybatis 表现层：页面展示 业务层：逻辑处理 持久层：持久数据化保存 在这里插入图片描述 Mybatis快速入门 
ESP32读取DHT11温湿度数据
芯片：ESP32 环境：Arduino 一、安装DHT11传感器库 红框的库，别安装错了 二、代码 注意，DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...
SpringTask-03.入门案例
一.入门案例 启动类： package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...
Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...
华硕a豆14 Air香氛版，美学与科技的馨香融合
在快节奏的现代生活中，我们渴望一个能激发创想、愉悦感官的工作与生活伙伴，它不仅是冰冷的科技工具，更能触动我们内心深处的细腻情感。正是在这样的期许下，华硕a豆14 Air香氛版翩然而至，它以一种前所未有的方式&#x…...
HashMap中的put方法执行流程（流程图）
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中，其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下： 初始判断与哈希计算： 首先，putVal 方法会检查当前的 table（也就…...
C++使用 new 来创建动态数组
问题： 不能使用变量定义数组大小 原因： 这是因为数组在内存中是连续存储的，编译器需要在编译阶段就确定数组的大小，以便正确地分配内存空间。如果允许使用变量来定义数组的大小，那么编译器就无法在编译时确定数组的大…...
GitFlow 工作模式（详解）
今天再学项目的过程中遇到使用gitflow模式管理代码，因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存，无论是github还是gittee，都是一种基于git去保存代码的形式，这样保存代码…...
【Linux】Linux 系统默认的目录及作用说明
博主介绍：✌全网粉丝23W，CSDN博客专家、Java领域优质创作者，掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围：SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...