《设计模式之美》读书笔记2
从Linux学习应对大型复杂项目的方法：
1、封装与抽象：封装了不同类型设备的访问细节，抽象为统一的文件访问方式，更高层的代码就能基于统一的访问方式，来访问底层不同类型的设备。这样做的好处是，隔离底层设备访问的复杂性。统一的访问方式能够简化上层代码的编写，并且使代码更容易复用。除此之外，抽象和封装还能有效控制代码复杂性的蔓延，将复杂性封装在局部代码中，隔离实现的易变性，提供简单、统一的访问接口，其他模块使用会更简单。其他模块基于抽象的接口而非具体实现编程，代码会更加稳定。
2、分层与模块化：不同模块之间使用接口进行通信，模块之间的耦合很小，每个团队聚焦于一个独立的高内聚模块来开发，最终像搭积木一样将各个模块组装起来构成一个复杂的系统。Unix系统本身也是基于分层开发的，他可以分为三层，分别是内核层、系统调用和应用层。每一层都对上层封装实现细节，暴露抽象的接口来调用。而且任意一层都可以重新被实现，不会影响到其他层的代码。
3、基于接口通信：在设计模块或者层要暴露的接口时，我们要学会隐藏实现，接口从命名到定义都要抽象一下，尽量减少涉及具体的实现细节。
4、高内聚低耦合
相关文章：
《设计模式之美》读书笔记2
从Linux学习应对大型复杂项目的方法： 1、封装与抽象：封装了不同类型设备的访问细节，抽象为统一的文件访问方式，更高层的代码就能基于统一的访问方式，来访问底层不同类型的设备。这样做的好处是，隔离底层设备…...
C++ STL set_difference 用法
一：功能 给定两个集合A，B；计算集合的差集，即计算出那些只包含在A中而不包含在B中的元素。 二：用法 #include <vector> #include <algorithm> #include <iostream>int main() {std::vector<int&…...
【基础算法总结】优先级队列
优先级队列 1.最后一块石头的重量2.数据流中的第 K 大元素4.前K个高频单词4.数据流的中位数 点赞👍👍收藏🌟🌟关注💖💖 你的支持是对我最大的鼓励，我们一起努力吧!😃😃 1…...
python-绝对值排序（赛氪OJ）
[题目描述] 输入 n 个整数，按照绝对值从大到小排序后输出。保证所有整数的绝对值不同。输入格式： 输入数据有多组，每组占一行，每行的第一个数字为 n ,接着是 n 个整数， n0 表示输入数据的结束，不做处理。输…...
成功者的几个好习惯，你具备了几个
每个人都想成为自己领域的佼佼者，然而，成功并非偶然，它往往与一系列良好的习惯紧密相连。这些习惯如同灯塔，指引着成功者在波涛汹涌的大海中稳健前行。 一、设定明确目标 没有明确的目标，就如同航海没有指南针&#…...
centos中zabbix安装、卸载及遇到的问题
目录 Zabbix简介Zabbix5.0和Zabbix7.0的区别监控能力方面模板和 API 方面性能、速度方面 centos7安装Zabbix(5.0)安装zabbix遇到的问题卸载Zabbix Zabbix简介 Zabbix 是一个基于 WEB 界面的提供分布式系统监视以及网络监视功能的企业级的开源解决方案。zabbix 能监视各种网络参…...
php编译安装
一、基础环境准备 # php使用www用户 useradd -s /sbin/nologin -M www二、下载php包 # 下载地址 https://www.php.net/downloads wget https://www.php.net/distributions/php-8.3.9.tar.gz三、配置编译安装 编译安装之前需要处理必要的依赖，在编译配置安装&…...
)
[K8S] K8S资源控制器Controller Manager(4)
文章目录 1. 常见的Pod控制器及含义2. Replication Controller控制器2.1 部署ReplicaSet 3. Deployment3.1部署Deployment3.2 运行Deployment3.3 镜像更新方式3.4 Deployment扩容3.5 滚动更新3.6 金丝雀发布(灰度发布)3.7 Deployment版本回退3.8 Deployment 更新策略 4. Daemon…...
C#，.NET常见算法
1.递归算法 1.1.C#递归算法计算阶乘的方法 using System;namespace C_Sharp_Example {public class Program{/// <summary>/// 阶乘：一个正整数的阶乘Factorial是所有小于以及等于该数的正整数的积，0的阶乘是1，n的阶乘是n࿰…...
KubeSphere介绍及一键安装k8s
KubeSphere介绍 官网地址：https://kubesphere.io/zh/ KubeSphere愿景是打造一个以 Kubernetes 为内核的云原生分布式操作系统，它的架构可以非常方便地使第三方应用与云原生生态组件进行即插即用（plug-and-play）的集成࿰…...
Spring 系列
SpringBoot 实体类（Entity）层 实体类（Entity）通常属于模型层（Model Layer）或领域层（Domain Layer）。它们代表应用程序中的核心业务数据结构，与数据库表结构紧密对应。在…...
基于opencv[python]的人脸检测
1 图片爬虫 这里的代码转载自：http://t.csdnimg.cn/T4R4F # 获取图片数据 import os.path import fake_useragent import requests from lxml import etree# UA伪装 head {"User-Agent": fake_useragent.UserAgent().random}pic_name 0 def request_pic…...
配置SSH公钥互信
目录 第一台主机：servera（172.25.250.101） 第一步：查看 . ssh目录下面是否为空 第二步：输入命令ssh-keygen 第三步： 再看查看一下. ssh目录 第四步： 输入命令 ssh-copy-id root172.25.250…...
WEB渗透Web突破篇-SQL注入（MSSQL）
注释符 -- 注释 /* 注释 */用户 SELECT CURRENT_USER SELECT user_name(); SELECT system_user; SELECT user;版本 SELECT version主机名 SELECT HOST_NAME() SELECT hostname;列数据库 SELECT name FROM master..sysdatabases; SELECT DB_NAME(N); — for N 0, 1, 2, ……...
DAY15
数组 冒泡排序 冒泡排序无疑是最为出名的排序算法之一，总共有八大排序 冒泡的代码还是相当简单的，两层循环，外层冒泡轮数，里层依次比较，江湖中人人尽皆知 我们看到嵌套循环，应该马上就可以得到这个算法的…...
pytest结合allure-pytest插件生成测试报告
目录 一、安装allure-pytest插件 二、下载allure 三、生成allure报告 四、效果展示 一、安装allure-pytest插件 二、下载allure 下载之后解压，解压之后还要配置环境变量（把allure目录下bin目录配置到系统变量的path路径），下…...
详细解析用户提交咨询
上一篇文章中写到了使用Server-Sent Events (SSE)，并获取message里面的内容。 本篇文章主要是写，具体该如何实现的具体代码，代码见下方，可直接拿 async submitConsult() {this.scrollToBottom();if (!this.$checkLogin()) return;…...
UDP/TCP协议解析
我最近开了几个专栏，诚信互三！ > |||《算法专栏》：：刷题教程来自网站《代码随想录》。||| > |||《C专栏》：：记录我学习C的经历，看完你一定会有收获。||| > |||《Linux专栏》࿱…...
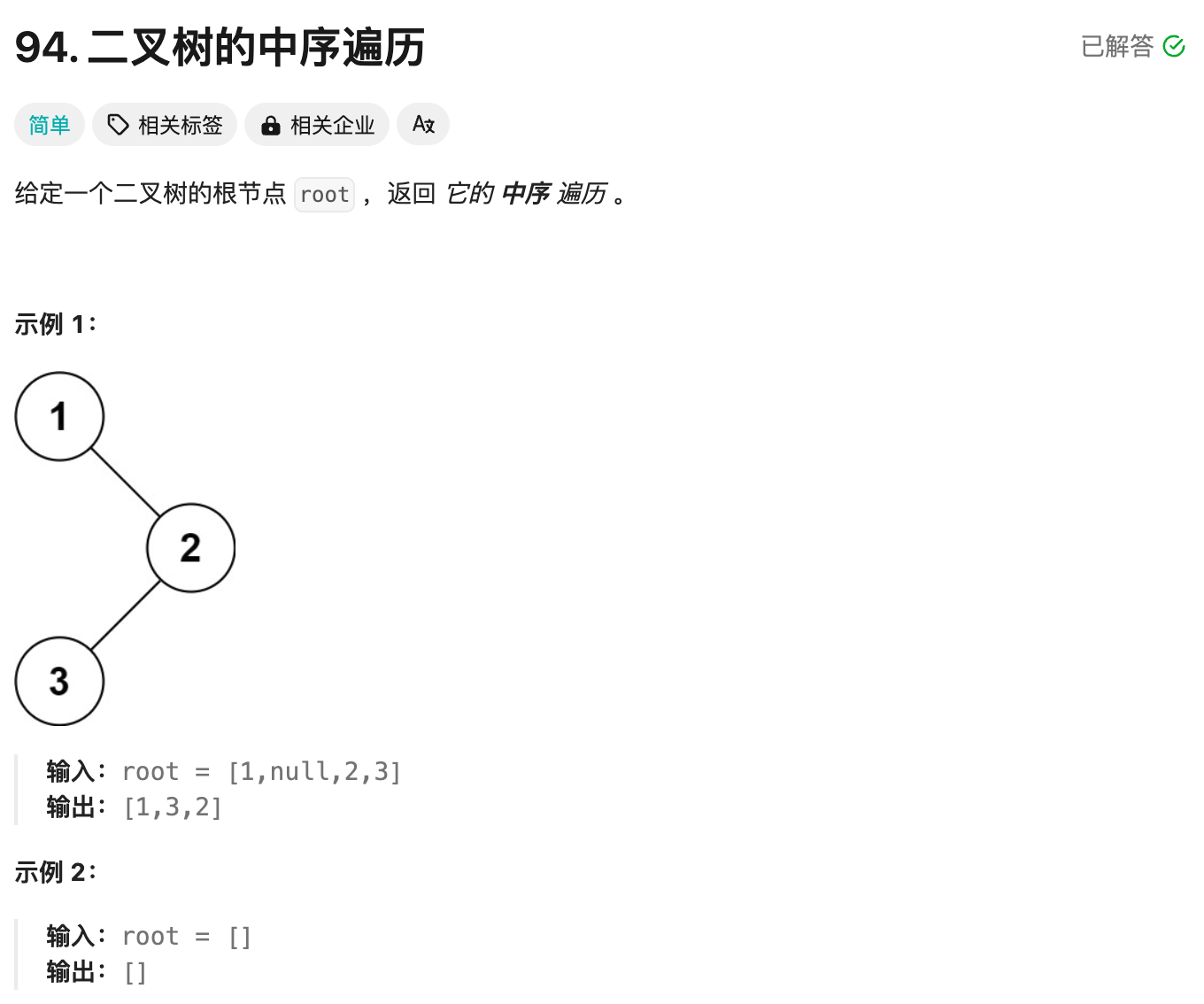
力扣94题（java语言）
题目 思路 使用一个栈来模拟递归的过程，以非递归的方式完成中序遍历(使用栈可以避免递归调用的空间消耗)。 遍历顺序步骤： 遍历左子树访问根节点遍历右子树 package algorithm_leetcode;import java.util.ArrayList; import java.util.List; import…...
JavaScript基础入门：构建动态Web世界的基石
简要介绍JavaScript作为互联网上最流行的编程语言之一，它在构建交互式网页、动态Web应用及服务器后端（通过Node.js）中的重要性。强调学习JS对于任何想要进入Web开发领域的人来说是不可或缺的。 1. JavaScript是什么？ 定义JavaSc…...
浏览器访问 AWS ECS 上部署的 Docker 容器（监听 80 端口）
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义（Task Definition&…...
业务系统对接大模型的基础方案：架构设计与关键步骤
业务系统对接大模型：架构设计与关键步骤 在当今数字化转型的浪潮中，大语言模型（LLM）已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中，不仅可以优化用户体验，还能为业务决策提供…...
《Qt C++ 与 OpenCV：解锁视频播放程序设计的奥秘》
引言：探索视频播放程序设计之旅 在当今数字化时代，多媒体应用已渗透到我们生活的方方面面，从日常的视频娱乐到专业的视频监控、视频会议系统，视频播放程序作为多媒体应用的核心组成部分，扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上，用户都期望…...
【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中，有几种方法可以执行Shell指令： 1. 使用system()函数 这是最简单的方法，包含在stdlib.h头文件中： #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...
Opencv中的addweighted函数
一.addweighted函数作用 addweighted（）是OpenCV库中用于图像处理的函数，主要功能是将两个输入图像（尺寸和类型相同）按照指定的权重进行加权叠加（图像融合），并添加一个标量值&#x…...
服务器硬防的应用场景都有哪些？
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式，避免服务器受到各种恶意攻击和网络威胁，那么，服务器硬防通常都会应用在哪些场景当中呢？ 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...
全志A40i android7.1 调试信息打印串口由uart0改为uart3
一，概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本：2014.07； Kernel版本：Linux-3.10； 二，Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01)，并让boo…...
Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明：这是一个机器学习实战项目（附带数据代码文档），如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下，风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...
鸿蒙（HarmonyOS5）实现跳一跳小游戏
下面我将介绍如何使用鸿蒙的ArkUI框架，实现一个简单的跳一跳小游戏。 1. 项目结构 src/main/ets/ ├── MainAbility │ ├── pages │ │ ├── Index.ets // 主页面 │ │ └── GamePage.ets // 游戏页面 │ └── model │ …...
多元隐函数 偏导公式
我们来推导隐函数 z z ( x , y ) z z(x, y) zz(x,y) 的偏导公式，给定一个隐函数关系： F ( x , y , z ( x , y ) ) 0 F(x, y, z(x, y)) 0 F(x,y,z(x,y))0 🧠 目标： 求 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z、 …...