*算法训练（leetcode）第三十一天 | 1049. 最后一块石头的重量 II、494. 目标和、474. 一和零

*1049. 最后一块石头的重量 II

leetcode题目地址

本题与分割等和子集类似，要达到碰撞最后的石头重量最小，则尽可能把石头等分为两堆。

时间复杂度： $O(m\ast n)$
空间复杂度： $O(n)$

// c++
class Solution {
public:int lastStoneWeightII(vector<int>& stones) {int sum = 0;for(int i=0; i<stones.size(); i++){sum += stones[i];}int target = sum/2;vector dp(target+1, 0);for(int i=0; i<stones.size(); i++){for(int j=target; j>=stones[i]; j--){dp[j] = max(dp[j], dp[j-stones[i]]+stones[i]);}}return sum - dp[target] - dp[target];}
};

*494. 目标和

leetcode题目地址

nums中元素初始均为正，先求其和sum。若|target|>sum，则无解。

需要推导出递推公式：设“+”数之和为X，则“-”数之和就是sum-X，其中，sum和target为已知。
可得递推公式：$$X-(sum-X)=target$$
解得：$$X=(target+sum)/2$$

因此， (target + sum) % 2 != 0时 无解。

一维dp数组记录背包容量为j时可以组成target的方案数量。

例如：target = 5

• 当前已有1，则有dp[4]种方案
• 当前已有2，则有dp[3]种方案
• 当前已有k，则有dp[target-k]种方案

时间复杂度： $O(n\ast m)$
空间复杂度： $O(n)$

// c++
class Solution {
public:int findTargetSumWays(vector<int>& nums, int target) {int sum = 0;for(int i=0; i<nums.size(); i++){sum += nums[i];}if(fabs(target)>sum) return 0;if((sum+target)%2!=0) return 0;vector<int> dp((target+sum)/2+1, 0);dp[0] = 1;for(int i=0; i<nums.size(); i++){for(int j=(target+sum)/2; j>=nums[i]; j--){dp[j] += dp[j-nums[i]]; }}return dp[(target+sum)/2];}
};

474. 一和零

leetcode题目地址

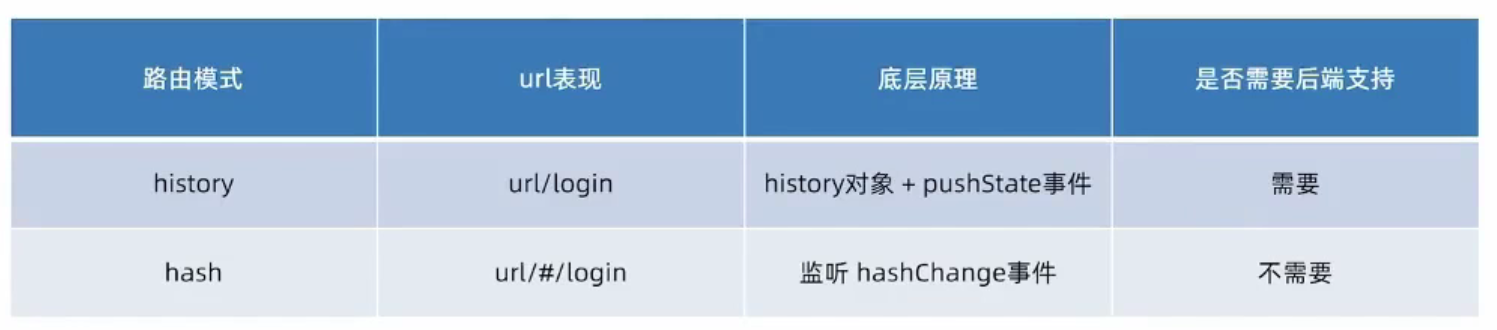
使用二维dp数组，横纵坐标分别代表0和1的背包容量，即dp[i][j]代表至多包含i个0和j个1的最多子串个数。

状态转移方程：$$dp[i][j]=max(dp[i][j],dp[i-zeroNum][j-oneNum]+1)$$

时间复杂度： $O(m\ast n\ast k)$
空间复杂度： $O(n\ast m)$

// c++
class Solution {
public:int findMaxForm(vector<string>& strs, int m, int n) {vector<int> zeros(strs.size(), 0);vector<int> ones(strs.size(), 0);for(int i=0; i<strs.size(); i++){for(int j=0; j<strs[i].size(); j++){if(strs[i][j] == '0') zeros[i]++;else ones[i]++;}}vector<vector<int>> dp(m+1, vector<int>(n+1, 0));for(int k=0; k<strs.size(); k++){for(int i=m; i>=zeros[k]; i--){for(int j=n; j>=ones[k]; j--){dp[i][j] = max(dp[i][j], dp[i-zeros[k]][j-ones[k]]+1);}}}return dp[m][n];}
};