机器学习 | 回归算法原理——最小二乘法
Hi,大家好,我是半亩花海。很早便想学习并总结一本很喜欢的机器学习图书——立石贤吾的《白话机器学习的数学》,可谓通俗易懂,清晰形象。那就在此分享并作为学习笔记来记录我的学习过程吧!本章的回归算法原理基于《基于广告费预测点击量》项目,欢迎大家交流学习!
目录
一、最小二乘法概述
二、案例分析
1. 设置问题
2. 定义模型
3. 最小二乘法
一、最小二乘法概述
最小二乘法(又称最小平方法)是一种数学优化技术。它通过最小化误差的平方和()寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小。最小二乘法同梯度下降类似,都是一种求解无约束最优化问题的常用方法,并且也可以用于曲线拟合,来解决回归问题。
二、案例分析
下面根据《基于广告费预测点击量》这一项目展开最小二乘法的介绍和分析。
1. 设置问题
假设存在这样一个前提:投入的广告费越多,广告的点击量就越高,进而带来访问数的增加。这样看这种假设类似于线性关系,但实际上两者之间未必是简单的线性关系。
根据广告费和实际点击量的对应关系数据,可以将两个变量用下面的图展示出来,如下图(图中的值是随便选的)。

我们看着这张图可以猜猜,如果花了200日元的广告费,广告的点击量会是多少呢?通过探索估计,大概在500次左右吧。

这就是机器学习。我们所做的事情正是从数据中进行学习,然后给出预测值。接下来我们就要使用机器学习,像我们刚才做的那样尝试进行根据广告费预测点击量的任务。
当然,实际要使用机器学习来解决的问题都会更复杂,很多问题无法像这样画出图来。现在我们为了加深理解才用了这样一个简单的例子,后面的例子会越来越难的。
2. 定义模型
那我们如何应用机器学习呢?就刚刚的例子,如下图所示,我们可以把图想象为函数。只要知道通过图中各点的函数的形式就能根据广告费得知点击量了。但是点击量经常变化,这叫作“点击量中含有噪声”,所以函数并不能完美地通过所有的点。

这样看便是我们初中便学过的一次函数,考虑到后面的学习(为了防止当未知数增加时,表达式中大量出现 a、b、c、d…这样的符号),我们常常使用如下的“ + 数字下标”的形式来表示未知数和推测值,进而定义一次函数的表达式。
比如,我们先任取两个数作为 、
,假设
,
,那么当广告费为 100 日元时,点击量的计算过程如下:
函数 y = 1 + 2x 的部分点信息如下:

但实际上我们再看一下刚才的图会发现,如果广告费为 100 日元,那 么点击量应该大于 400。

这说明我们刚才确定的参数 ,
完全不正确。 接下来我们就要使用机器学习来求出正确的
和
的值。
3. 最小二乘法
假设有 n 个训练数据, 那么它们的误差之和可以用下面的表达式 表示。这个表达式称为目标函数(其中,
的 E 是误差的英语单词 Error 的首字母)。(ps:计算误差一般不用绝对值,而用平方。因为之后要对目标函数进行微分,比起绝对值,平方的微分更加简单。)
其中, 表达式为:
其次, 和
中的 i 不是 i 次幂的意思,而是指第 i 个训练数据。
再者,误差解释一下,如下图所示,图中的双向虚线箭头表示训练数据的点和 图像的误差。

我们实际来计算一下表达式 中
的值吧。设
,
, 然后将刚才列举的 4 个训练数据代入表达式。求出来的误差有点大……
上述结果 112 176.5 这个值本身没有什么意义,我们要通过一些方法修改参数 ,如之后所学习的神经网络中的调参等方式,使得这个值变得越来越小。这种做法称为最小二乘法。
相关文章:
机器学习 | 回归算法原理——最小二乘法
Hi,大家好,我是半亩花海。很早便想学习并总结一本很喜欢的机器学习图书——立石贤吾的《白话机器学习的数学》,可谓通俗易懂,清晰形象。那就在此分享并作为学习笔记来记录我的学习过程吧!本章的回归算法原理基于《基于…...

.NET Core 中的字符串压缩方法
字符串压缩的概念 字符串压缩通常指的是通过算法减少字符串表示所需的数据量,同时保持字符串的原始信息或能够无损地恢复原始字符串。这种压缩可以是针对文本数据的特定算法,也可以是更通用的数据压缩算法。 .NET Core 中的字符串压缩方法 使用数据压…...

SQL 基础知识
SQL(结构化查询语言)是一种用于管理和操作关系数据库的标准编程语言。以下是一些 SQL 的基础知识: 基本概念 数据库(Database): 存储和管理数据的容器。一个数据库可以包含多个表。 表(Table&…...

【数据结构初阶】单链表经典算法题十二道——得道飞升(上篇)
目录 1、移除元素 2、反转链表 3、链表的中间节点 4、合并两个有序链表 Relaxing Time!!! ———————————————— 天气之子幻 ———————————————— 1、移除元素 思路: 创建一个新链表࿰…...

Python爬虫技术 第16节 XPath
XPath是一种在XML文档中查找信息的语言,尽管XML和HTML在语法上有区别,但XPath同样适用于HTML文档的解析,尤其是在使用如lxml这样的库时。XPath提供了一种强大的方法来定位和提取XML/HTML文档中的元素和属性。 XPath基础 XPath表达式由路径表…...

本地部署,Whisper: 开源语音识别模型
目录 简介 特点 应用 使用方法 总结 GitHub - openai/whisper: Robust Speech Recognition via Large-Scale Weak SupervisionRobust Speech Recognition via Large-Scale Weak Supervision - openai/whisperhttps://github.com/openai/whisper 简介 Whisper 是一个由 O…...

history,hash缓存那些事
vue-router 中的 createWebHistory,createWebHashHistory两种模式 createWebHistory 是基于 window.history 对象是HTML5提供的用于维护当前标签页浏览历史的对象,主要功能是前进后退和在不刷新页面的情况下,修改地址栏里的URL地址。histor…...

Spring Boot的Web开发
目录 Spring Boot的Web开发 1.静态资源映射规则 第一种静态资源映射规则 2.enjoy模板引擎 3.springMVC 3.1请求处理 RequestMapping DeleteMapping 删除 PutMapping 修改 GetMapping 查询 PostMapping 新增 3.2参数绑定 一.支持数据类型: 3.3常用注解 一.Request…...

Spark 解析嵌套的 JSON 文件
1、什么是嵌套的JSON文件? 嵌套的JSON文件是指文件中包含了嵌套的JSON对象或数组。例如,以下是一个嵌套的JSON文件的示例: {"name": "John","age": 30,"address": {"street": "123…...
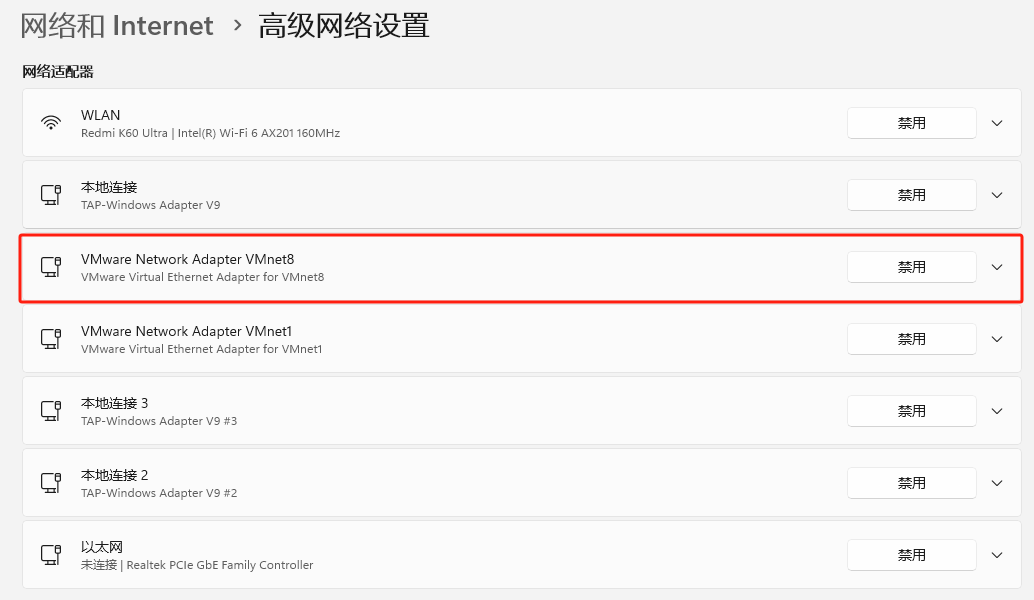
VMware虚拟机中CentOS7自定义ip地址并且固定ip
配置固定ip(虚拟机) 前提:虚拟机网络配置成,自定义网络并选择VMnet8(NAT 模式) 操作(如下图):点击虚拟机–》设置–》–》硬件–》网络适配器–》自定义:特定虚拟网络–》选择:VMnet8(NAT 模式) 虚拟机网络设置 需要记…...

CCS(Code Composer Studio 10.4.0)编译软件中文乱码怎么解决
如果是所有文件都出现了中文乱码这时建议直接在窗口首选项中修改:选择"Window" -> "Preferences",找到"General" -> "Workspace",将"Text file encoding"选项设置为"Other&quo…...

Flutter 3 完全支持网页端
Flutter 3 可以用于开发网页端应用。自 Flutter 2.0 起,Flutter 就已经支持 Web 平台,并且在 Flutter 3 中得到了进一步的改进和优化。以下是使用 Flutter 3 开发网页端的一些优势和特点: Flutter 3 开发网页端的优势: 跨平台一致…...

vue.js入门
目录 一. 框架概述 二. vue常用命令 2.1 插值表达式 2.2 v-text 2.3 v-html 2.4 v-on 2.5 v-model 2.6 v-show 2.7 v-if 2.8 v-else 2.9 v-bind 2.10 v-for 三. vue生命周期函数 目录 一. 框架概述 二. vue常用命令 2.1 插值表达式 2.2 v-text 2.3 v-html 2…...

API签名认证
前言(项目背景): 这个API签名认证是API开放平台得一个重要环节,我们知道,这个API开发平台,用处就是给客户去调用现成得接口来完成某些事情得。 在讲API签名认证之前,我们先模拟一个场景并且介绍…...
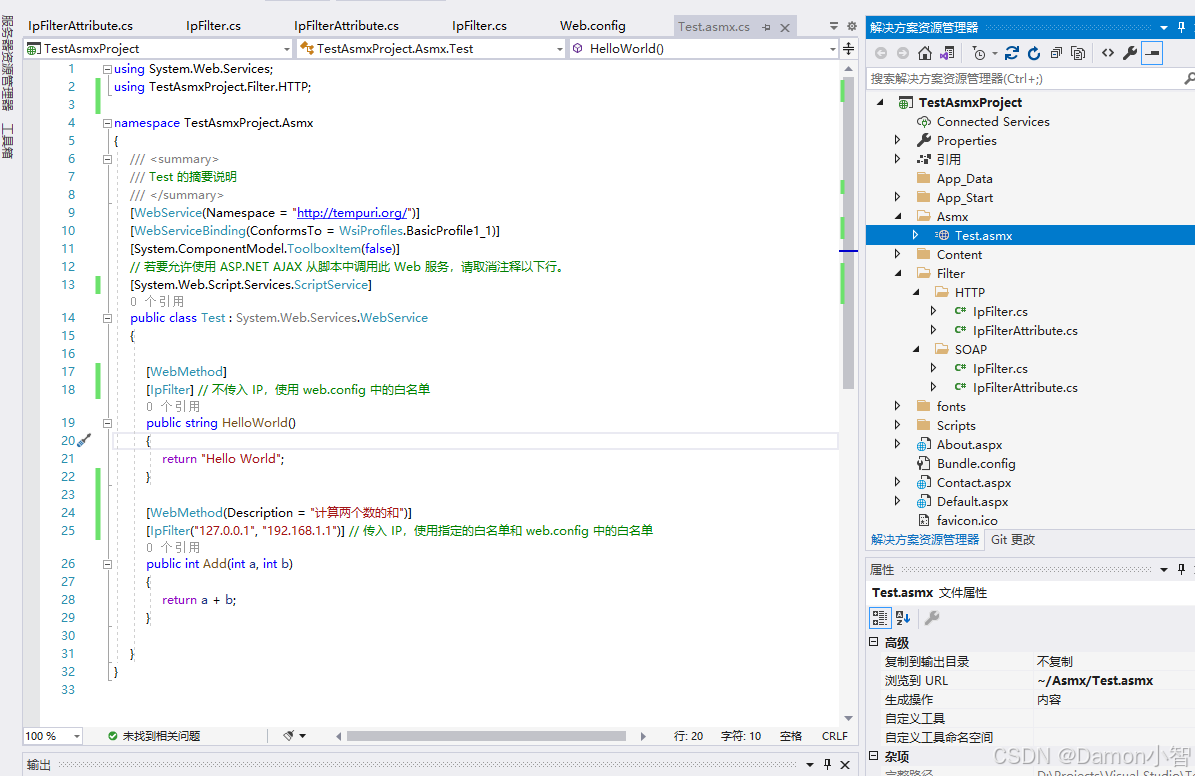
C#进阶-基于.NET Framework 4.x框架实现ASP.NET WebForms项目IP拦截器
在这篇文章中,我们将探讨如何在 ASP.NET WebForms 中实现IP拦截器,以便在 ASMX Web 服务方法 和 HTTP 请求 中根据IP地址进行访问控制。我们将使用自定义的 SoapExtension 和 IHttpModule 来实现这一功能,并根据常用的两种文本传输协议&#…...

前端(1)HTML
1、标签 创建1.html文件,浏览器输入E:/frontheima/1.html,可以访问页面 页面展示 在VSCODE安装IDEA的快捷键,比如ctld复制一行、ctrlx剪切 <p id"p1" title"标题1">Hello,world!</p> <p id"p2"…...

【北京迅为】《i.MX8MM嵌入式Linux开发指南》-第三篇 嵌入式Linux驱动开发篇-第五十三章 设备树下的platform驱动
i.MX8MM处理器采用了先进的14LPCFinFET工艺,提供更快的速度和更高的电源效率;四核Cortex-A53,单核Cortex-M4,多达五个内核 ,主频高达1.8GHz,2G DDR4内存、8G EMMC存储。千兆工业级以太网、MIPI-DSI、USB HOST、WIFI/BT…...

Java正则表达式判断有无特殊字符
//^代表否定,匹配除了数字、字母、下划线的特殊字符。 private static final String SPECIAL_CHAR_PATTERN "[^a-zA-Z0-9_]"; Pattern pattern Pattern.compile(SPECIAL_CHAR_PATTERN); Matcher matcher pattern.matcher(userAccount); // 如果 find(…...

使用Java和Spring AMQP构建消息驱动应用
使用Java和Spring AMQP构建消息驱动应用 大家好,我是微赚淘客系统3.0的小编,是个冬天不穿秋裤,天冷也要风度的程序猿! 消息驱动应用程序在现代系统架构中扮演着重要角色,特别是在处理高并发和异步任务时。Spring AMQ…...

【NLP】提升文本生成多样性的实用方法
比如用T5模型,训练数据是inputText-outputText格式,预测时do_sample=False # 预测代码from transformers import TFAutoModelForSeq2SeqLM from transformers import AutoTokenizercheckpoint_local = "./path/" tokenizer = AutoTokenizer.from_pretrained(check…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

JavaScript基础-API 和 Web API
在学习JavaScript的过程中,理解API(应用程序接口)和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能,使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...

Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...

Spring Security 认证流程——补充
一、认证流程概述 Spring Security 的认证流程基于 过滤器链(Filter Chain),核心组件包括 UsernamePasswordAuthenticationFilter、AuthenticationManager、UserDetailsService 等。整个流程可分为以下步骤: 用户提交登录请求拦…...
与文本切分器(Splitter)详解《二》)
LangChain 中的文档加载器(Loader)与文本切分器(Splitter)详解《二》
🧠 LangChain 中 TextSplitter 的使用详解:从基础到进阶(附代码) 一、前言 在处理大规模文本数据时,特别是在构建知识库或进行大模型训练与推理时,文本切分(Text Splitting) 是一个…...
