Java中的二叉树
文章目录
- 前言
- 一、树形结构(了解)
- 1.1 概念
- 1.2 概念(重要)
- 1.3 树的表示形式(了解)
- 1.4 树的应用
- 二、二叉树(重点)
- 2.1 概念
- 2.2 两种特殊的二叉树
- 2.3 二叉树的性质
- 2.5 二叉树的存储
- 2.5 二叉树的基本操作
- 2.5.1 前置说明
- 2.5.2 二叉树的遍历
- 2.5.3 二叉树的基本操作
- 总结
前言
一、树形结构(了解)
1.1 概念
树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一颗倒挂的树,也就是说它是根朝上,而叶朝下的。它具有以下的特点:
- 有一个特殊的结点,称为根结点,根结点没有前驱结点
- 除根结点以外,其余结点被分成M(M>0)个互不相交的集合,其中每一个集合又是一颗与树类似的子树。每颗子树的根结点有且只有一个前驱,可以有0个或者多个后继。
- 树是递归定义的
注意:树形结构中,子树之间不能有交集,否则就不是树形结构
1.2 概念(重要)
- 结点的度:一个结点含有子树的个数称为该结点的度
- 树的度:一棵树中,所有结点度的最大值称为树的度
- 叶子结点或终端结点:度为0的结点称为叶结点
- 双亲结点或父节点:若一个结点含有子结点,则这个结点称为其子结点的父结点
- 孩子结点或子节点:一个结点含有的子树的根结点称为该结点的子结点
- 根结点:一棵树中,没有双亲结点的结点
- 结点的层次:从根开始定义起,根为第1层,根的子结点为第2层,以此类推
- 树的高度或深度:树中结点的最大层次
树的以下概念只需了解,看见时知道什么意思即可:
- 非终端结点或分支结点:度不为0的结点
- 兄弟结点:具有相同父结点的结点互称为兄弟结点
- 堂兄弟结点:双亲在同一层的结点互为堂兄弟
- 结点的祖先:从根到该结点所经分支上的所有结点
- 子孙:以某结点为根的子树中任一结点都称为该结点的子孙
- 森林:有m(m>=0)颗互不相交的树组成的集合称为森林
1.3 树的表示形式(了解)
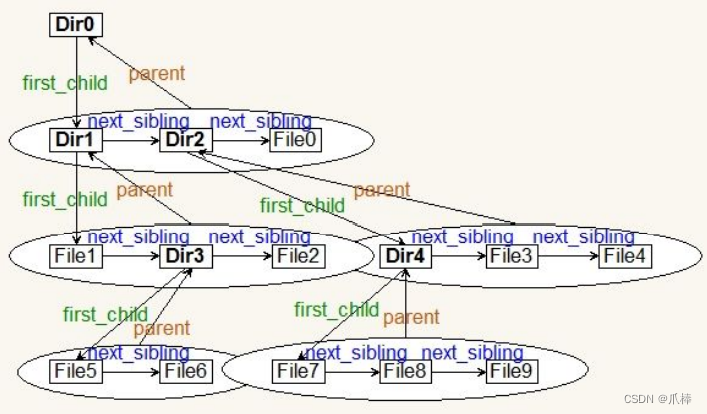
树结构相对线性表就比较复杂了,要存储表示起来就比较麻烦了,实际中树有很多种表示方式,如:双亲表示法,孩子表示法,孩子双亲表示法,孩子兄弟表示法等等。在这里我们就简单的介绍一下最常用的孩子兄弟表示法。
class Node {int value; //树中存储的数据Node firstChild; //第一个孩子引用Node nextBrother; //下一个兄弟引用
}
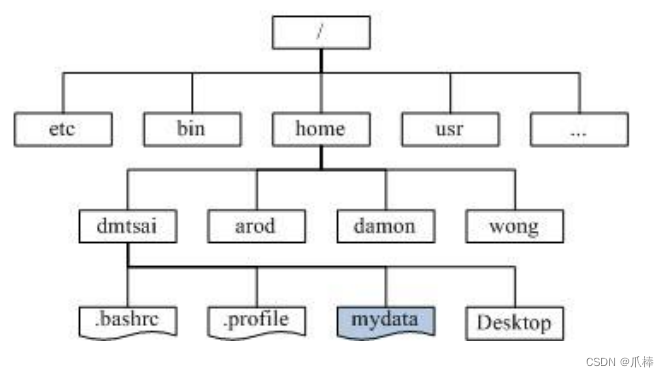
1.4 树的应用
文件系统管理(目录和文件)
二、二叉树(重点)
2.1 概念
一颗二叉树是结点的一个有限集合,该结合:
- 或者为空
- 或者是由一个根结点加上两颗分别称为左子树和右子树的二叉树组成
注意:
- 二叉树不存在度大于2的结点
- 二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树
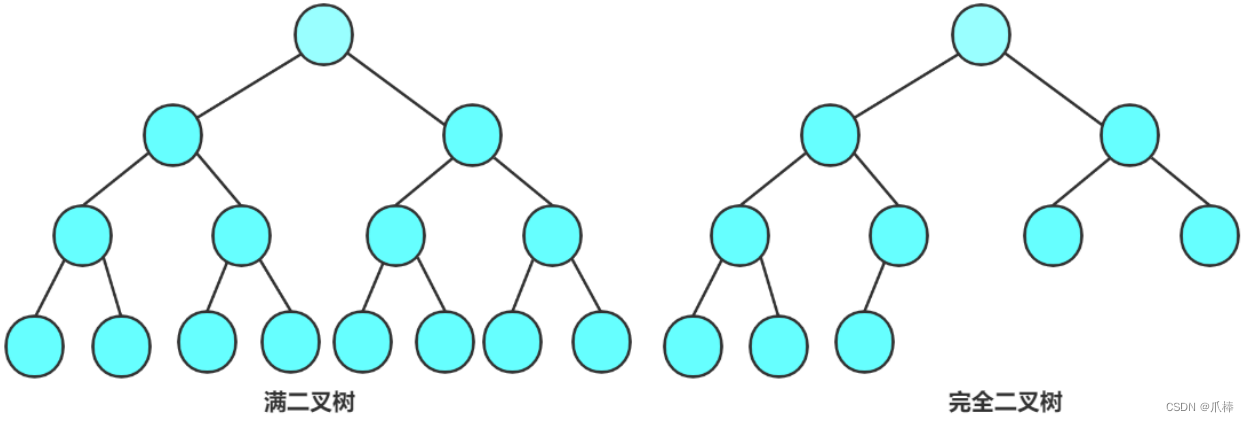
2.2 两种特殊的二叉树
- 满二叉树:一颗二叉树,如果每层的结点数都达到最大值,则这颗二叉树就是满二叉树。也就是说,如果一颗二叉树的层数为K,且结点总数是2^k-1,则它就是满二叉树。
- 完全二叉树:完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从0至n-1的结点一一对应时称之为完全二叉树。要注意的是,满二叉树是一种特殊的完全二叉树。
2.3 二叉树的性质
- 若规定根结点的层数为1,则一颗非空二叉树的第i层最多有2^(i-1) (i>0)个结点
- 若规定只有根结点的二叉树的深度为1,则深度为K的二叉树的最大结点数是2^-1 (k>=0)
- 对任何一颗二叉树,如果其叶结点个数为n0,度为2的非叶结点个数为n2,则有n0=n2+1
- 具有**n个结点的完全二叉树的深度K为log2(n+1)**向上取整
- 对于具有n个结点的完全二叉树,如果按照从上至下从左至右的顺序对所有结点从0开始编号,则对于序号为i的结点有:
1.若i>0,双亲序号:(i-1)/2;i=0,i为根结点编号,无双亲结点
2.若2i+1<n,左孩子序号:2i+1,否则无左孩子
3.若2i+2<n,右孩子序号:2i+2,否则无右孩子
习题:
1. 某二叉树共有 399 个结点,其中有 199 个度为 2 的结点,则该二叉树中的叶子结点数为( )A 不存在这样的二叉树B 200C 198D 1992.在具有 2n 个结点的完全二叉树中,叶子结点个数为( )A nB n+1C n-1D n/23.一个具有767个节点的完全二叉树,其叶子节点个数为()A 383B 384C 385D 3864.一棵完全二叉树的节点数为531个,那么这棵树的高度为( )A 11B 10C 8D 12【参考答案】 1.B 2.A 3.B 4.B
2.5 二叉树的存储
二叉树的存储结构分为:顺序存储和类似于链表的链式存储。
二叉树的链式存储是通过一个一个的结点引用起来的,常见的表示方式有二叉和三叉表示方式,具体如下:
// 孩子表示法
class Node {int val; // 数据域Node left; // 左孩子的引用,常常代表左孩子为根的整棵左子树Node right; // 右孩子的引用,常常代表右孩子为根的整棵右子树
}
// 孩子双亲表示法
class Node {int val; // 数据域Node left; // 左孩子的引用,常常代表左孩子为根的整棵左子树Node right; // 右孩子的引用,常常代表右孩子为根的整棵右子树Node parent; // 当前节点的根节点
}
2.5 二叉树的基本操作
2.5.1 前置说明
在学习二叉树的基本操作前,需先要创建一棵二叉树,然后才能学习其相关的基本操作。为了降低大家学习成本,此处手动快速创建一棵简单的二叉树,快速进入二叉树操作学习,等二叉树结构了解的差不多时,我们反过头再来研究二叉树真正的创建方式。
public class BinaryTree{public static class BTNode{BTNode left;BTNode right;int value;BTNode(int value){this.value = value;}}private BTNode root;public void createBinaryTree(){BTNode node1 = new BTNode(1);BTNode node1 = new BTNode(2);BTNode node1 = new BTNode(3);BTNode node1 = new BTNode(4);BTNode node1 = new BTNode(5);BTNode node1 = new BTNode(6);root = node1;node1.left = node2;node2.left = node3;node1.right = node4;node4.left = node5;node5.right = node6;}
}
注意:上述代码并不是创建二叉树的方式。
2.5.2 二叉树的遍历
// 前序遍历 根 左子树 右子树 递归public void preOrder(TreeNode root) {if (root == null) {return;}System.out.print(root.val + " ");preOrder(root.left);preOrder(root.right);}//前序遍历 非递归public void proOrderNor(TreeNode root) {if(root==null) {return;}TreeNode cur = root;//栈Deque<TreeNode> stack = new ArrayDeque<>();while (cur!=null || !stack.isEmpty()) {while (cur!=null) {stack.push(cur);System.out.print(cur.val+" ");cur = cur.left;}TreeNode top = stack.pop();cur = top.right;}}//子问题思路public List<Integer> preorderTraversal(TreeNode root) {List<Integer> list = new ArrayList<>(); //利用好返回值if(root==null) {return list;}list.add((int) root.val);List<Integer> lefttree = preorderTraversal(root.left);list.addAll(lefttree);List<Integer> righttree = preorderTraversal(root.right);list.addAll(righttree);return list;}// 中序遍历public void inOrder(TreeNode root) {if(root == null) {return;}inOrder(root.left);System.out.print(root.val+" ");inOrder(root.right);}// 中序遍历 非递归public void inOrderNor(TreeNode root) {if(root == null) {return;}TreeNode cur = root;//栈Deque<TreeNode> stack = new ArrayDeque<>();while (cur!=null || !stack.isEmpty()) {while (cur!=null) {cur = cur.left;stack.push(cur);}TreeNode top = stack.pop();System.out.print(top.val+" ");cur = top.right;}}public List<Integer> inorderTraversal(TreeNode root) {List<Integer> list = new ArrayList<>();if(root==null) {return list;}List<Integer> lefttree = inorderTraversal(root.left);list.addAll(lefttree);list.add((int) root.val);List<Integer> righttree = inorderTraversal(root.right);list.addAll(righttree);return list;}// 后序遍历public void postOrder(TreeNode root) {if(root == null) {return;}postOrder(root.left);postOrder(root.right);System.out.print(root.val+" ");}// 后序遍历 非递归public void postOrderNor(TreeNode root) {if(root == null) {return;}TreeNode cur = root;TreeNode prev = null;//栈Deque<TreeNode> stack = new ArrayDeque<>();while (cur!=null || !stack.isEmpty()) {while (cur!=null) {stack.push(cur);cur = cur.left;}TreeNode top = stack.peek();cur = top.right;if(top.right==null || top.right == prev) {System.out.print(top.val+" ");stack.pop();prev = top;}else {cur = top.right;}}System.out.println();}
-
前中后序遍历
学习二叉树结构,最简单的方式就是遍历。所谓遍历,是指沿着某条搜索路线,依次对树中每个结点均做一次且仅做一次访问。访问结点所做的操作是依赖于具体的应用问题(比如:打印结点内容、结点内容加1)。遍历时二叉树上最重要的操作之一,是二叉树上进行其他运算之基础。在遍历二叉树时,如果没有进行某种约定,每个人都按照自己的方式进行遍历,得出的结果会比较混乱,如果按照某种规则进行约定,则每个人对于同一颗树的遍历结果肯定是相同的。如果N代表根结点,L代表根结点的左子树,R代表根结点的右子树,则根据遍历根结点的先后次序有以下遍历方式:
- NLR:前序遍历(先序遍历)-----访问根结点----->根的左子树----->根的右子树
- LNR:中序遍历-----根的左子树----->根结点----->根的右子树
- LRN:后序遍历-----根的左子树----->根的右子树----->根结点
-
层序遍历
除了先序遍历、中序遍历、后序遍历外,还可以对二叉树进行层序遍历。设二叉树的根结点所在层数为1,层序遍历就是从所在二叉树的根结点出发,首先访问第一层的树根结点,然后从左到右访问第2层上的结点,接着是第三层的结点,以此类推,自上而下,自左至右逐层访问树的结点的过程就是层序遍历。
习题:
1.某完全二叉树按层次输出(同一层从左到右)的序列为 ABCDEFGH 。该完全二叉树的前序序列为()A: ABDHECFG B: ABCDEFGH C: HDBEAFCG D: HDEBFGCA2.二叉树的先序遍历和中序遍历如下:先序遍历:EFHIGJK;中序遍历:HFIEJKG.则二叉树根结点为()A: E B: F C: G D: H3.设一课二叉树的中序遍历序列:badce,后序遍历序列:bdeca,则二叉树前序遍历序列为()A: adbce B: decab C: debac D: abcde4.某二叉树的后序遍历序列与中序遍历序列相同,均为 ABCDEF ,则按层次输出(同一层从左到右)的序列为()A: FEDCBA B: CBAFED C: DEFCBA D: ABCDEF【参考答案】 1.A 2.A 3.D 4.A
2.5.3 二叉树的基本操作
// 获取树中节点的个数 子问题思路public int size(TreeNode root) {if(root==null) {return 0;}int leftSize = size(root.left);int rightSize = size(root.right);return leftSize+rightSize+1;};// 获取树中节点的个数 遍历思路public static int len ;public void size1(TreeNode root) {if(root==null) {return ;}len++;size1(root.left);size1(root.right);};// 获取叶子节点的个数public int getLeafNodeCount(TreeNode root) {if(root==null) {return 0;}if(root.left==null && root.right==null) {return 1;}return getLeafNodeCount(root.left) + getLeafNodeCount(root.right);};// 获取第K层节点的个数public int getKLevelNodeCount(TreeNode root,int k){if(root==null) {return 0;}if(k==1) {return 1;}int leftsize = getKLevelNodeCount(root.left,k-1);int rightsize = getKLevelNodeCount(root.right,k-1);return leftsize+rightsize;};// 获取二叉树的高度public int getHeight(TreeNode root) {if(root==null) {return 0;}int leftHight = getHeight(root.left);int rightHight = getHeight(root.right);return (leftHight>rightHight)?(leftHight+1):(rightHight+1);};// 检测值为value的元素是否存在public TreeNode find(TreeNode root, int val){if(root==null) {return null;}if(root.val==val) {return root;}TreeNode leftTree = find(root.left,val);if(leftTree!=null) {return leftTree;}TreeNode rightTree = find(root.right,val);if(rightTree!=null) {return rightTree;}return null;};
总结
以上就是今天要讲的内容,本文介绍了二叉树的相关内容,二叉树在数据结构中属于重难点,需要大量刷题巩固基础。如有不正,望各位博友提出修改,谢谢大家。
相关文章:

Java中的二叉树
文章目录前言一、树形结构(了解)1.1 概念1.2 概念(重要)1.3 树的表示形式(了解)1.4 树的应用二、二叉树(重点)2.1 概念2.2 两种特殊的二叉树2.3 二叉树的性质2.5 二叉树的存储2.5 二…...
基于 gma 绘制古代洛阳 5 大都城遗址空间分布地图
了解 gma gma 是什么? gma 是一个基于 Python 的地理、气象数据快速处理和数据分析函数包(Geographic and Meteorological Analysis,gma)。gma 网站:地理与气象分析库。 gma 的主要功能有哪些? 气候气象&a…...
分析 Spring 的依赖注入模式
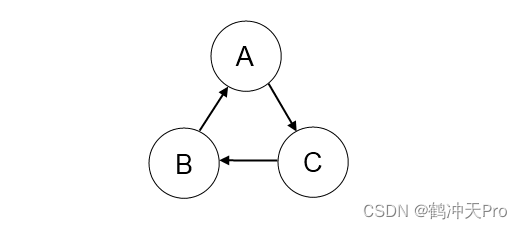
一、依赖注入二、Field Injection优点缺点三、Constructor Injection优点1. 容易发现 code smell优点2. 容易厘清依赖关系优点3. 容易写单元测试优点4. Immutable Object缺点:循环依赖四、总结一、依赖注入 依赖注入 (Dependency Injection,…...
IntelliJ IDEA创建Servlet
目录 ——————————————————————————————— 一、创建Java项目 1、创建java项目 2、选择java 3、next 4、给项目命名 5、新创建完java项目的目录结构 二、变java为servlet项目 1、变servlet项目 2、选择Web Application 3、更新完成后的目录…...

Spring Boot如何让自己的bean优先加载
背景介绍 在一些需求中,可能存在某些场景,比如先加载自己的bean,然后自己的bean做一些DB操作,初始化配置问题,然后后面的bean基于这个配置文件,继续做其他的业务逻辑。因此有了本文的这个题目。 实现方法…...
LeetCode分类刷题----动态规划
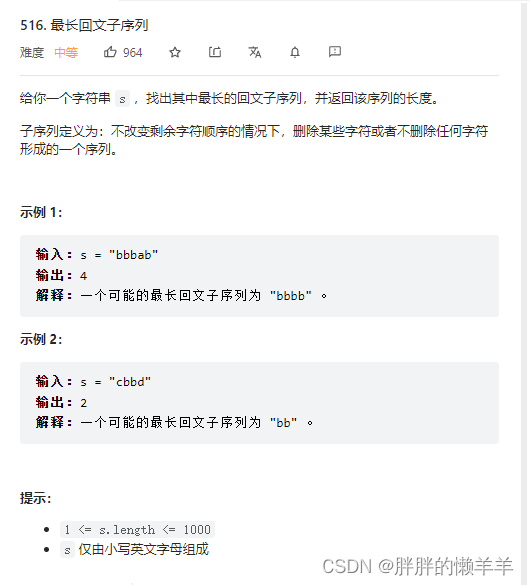
动态规划509.斐波那契数列70.爬楼梯746.使用最小花费怕楼梯62.不同路径63.不同路径||343.整数拆分96.不同的二叉搜索树01背包问题416.分割等和子集1049.最后一块石头的重量||494.目标和474.一和零完全背包问题518.零钱兑换||377.组合总和IV322.零钱兑换279.完全平方数139.单词拆…...

今年好像没有金三银四了?
大家好,我是记得诚。 金三银四,是换工作的高峰期,新的一年结束了,在年前拿完年终奖,在年后3月和4月换个满意的工作。 单从我公司来看,目前还没有一个人离职,往年离职率是要高一些的。 还有我…...
【C++】入门知识之 函数重载
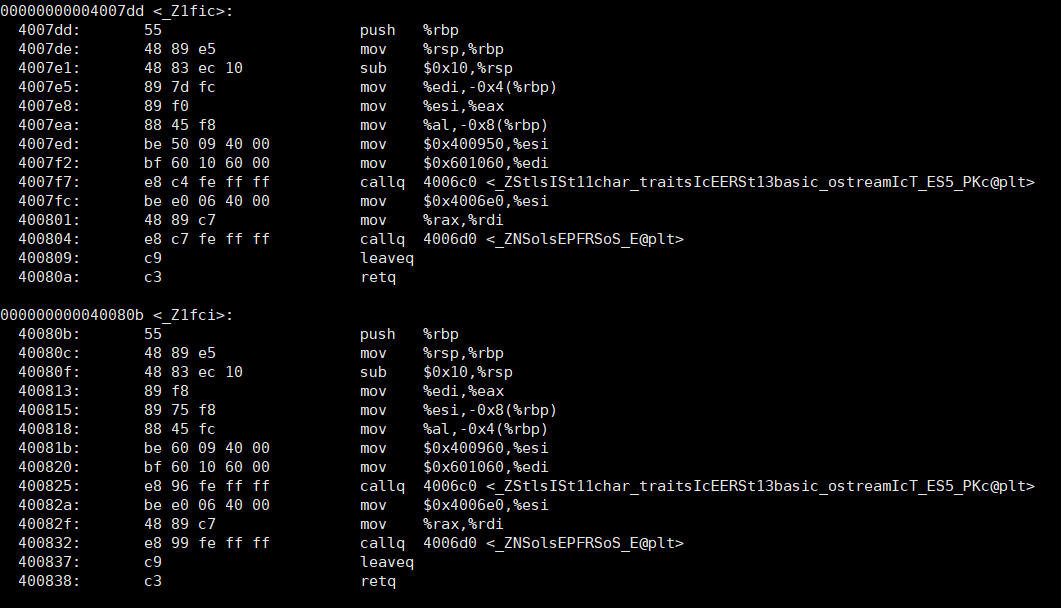
前言提到重载这个词,我们会想到什么呢?重载有一种一词多义的意思,中华文化博大精深,之前有一个笑话,中国的乒乓球谁都打不过,男足谁都打不过,哈哈哈这也是非常有意思的,但是今天我们…...
文心一言发布,你怎么看?chatGPT
百度全新一代知识增强大语言模型“文心一言”于2021年3月16日正式发布,作为一款自然语言处理技术,它引起了广泛的关注和讨论。 首先,文心一言是一款具有重大意义的自然语言处理技术。在人工智能领域,自然语言处理技术一直是一个难…...

字符函数和字符串函数【上篇】
文章目录🎖️1.函数介绍📬1.1. strlen📬1.2. strcpy📬1.3. strcat📬1.4. strcmp📬1.5. strncpy📬1.6. strncat📬1.7. strncmp🎖️1.函数介绍 📬1.1. strlen …...

list的模拟实现(模仿STL)
目录 一、模拟实现前的准备 1.list结构认识 2.迭代器的实现不同 3.如何实现需要的功能 二.结点类实现 三.迭代器实现 1.实现前的问题 2._list_iterator类的成员变量和构造函数 3.*和->运算符重载 4.前置和后置的实现 5.前置--和后置-- 6.和!运算符重载 四.list类的实现 1.li…...

05-STM32F1 - 串行通信SPI
SPI STM-SPI作为主机,从机 SPI的时钟,最高为Pclk/2,SPI1最高为36Mhz,SPI2最高为18Mhz。 SPI的四种模式 CPOL CPHA,数据帧8~16位,LSB,MSB 全双工,双向单线,单线 物理层 接口标准…...

【Pytorch】Tensor的分块、变形、排序、极值与in-place操作
本文参加新星计划人工智能(Pytorch)赛道:https://bbs.csdn.net/topics/613989052 这是目录Tensor的分块Tensor的变形Tensor的排序Tensor的极值Tensor的in-place操作Tensor是PyTorch中用于存储和处理多维数据的基本数据结构,它类似于NumPy中的ndarray&…...

数组栈的实现
个人主页:平行线也会相交 欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 平行线也会相交 原创 收录于专栏【数据结构初阶(C实现)】 目录所有接口函数栈的初始化在栈顶放数据释放数据删除数据取栈顶的数据判断栈取区是否为…...
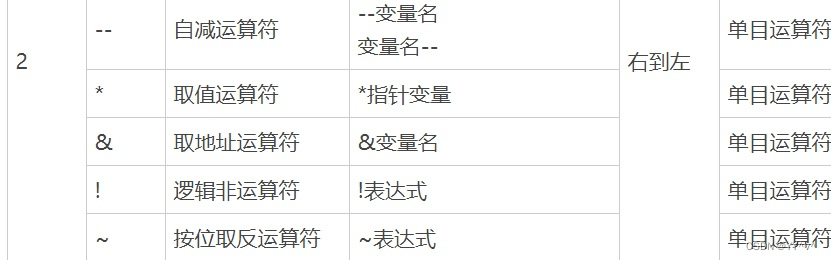
*p++,*(p++),*++p,(*p)++区别?
*p++:等同于:*p; p += 1; 解析:由于和++的运算优先级一样,且是右>结合。故p++相当于*(p++),p先与++结合,>然后p++整体再与结合。前面陈述是一种最 常见的错误,很多初学者也是这么理解的。 但是,因为++后置的时候,本身含义就是先 运算后增加1(运算指的是p++作为…...
又一个线上偶发问题-系统短暂无法获取到Redis连接
概述 最近不知道咋回事,老是在线上遇到偶发的故障,它突然出现,又很快消失了。 在2023年3月11下午差不多六点左右,我正在工位上喝着香味扑鼻的金骏眉红茶,突然接到了一个电话,拿起手机一看,是阿里…...
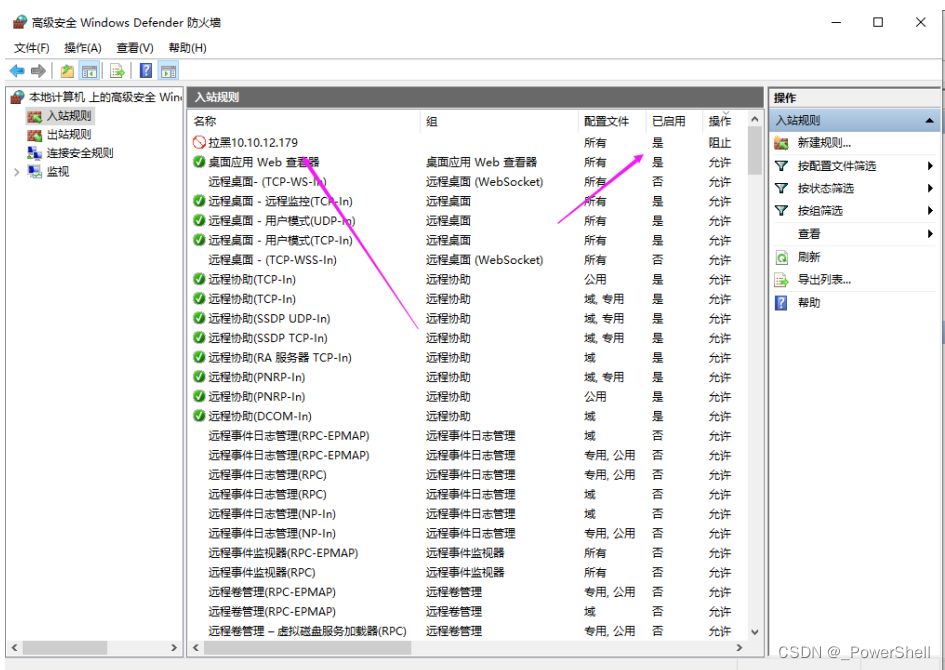
[ 系统安全篇 ] 拉黑IP - 火绒安全软件设置IP黑名单 windows使用系统防火墙功能设置IP黑名单
🍬 博主介绍 👨🎓 博主介绍:大家好,我是 _PowerShell ,很高兴认识大家~ ✨主攻领域:【渗透领域】【数据通信】 【通讯安全】 【web安全】【面试分析】 🎉点赞➕评论➕收藏 养成习…...
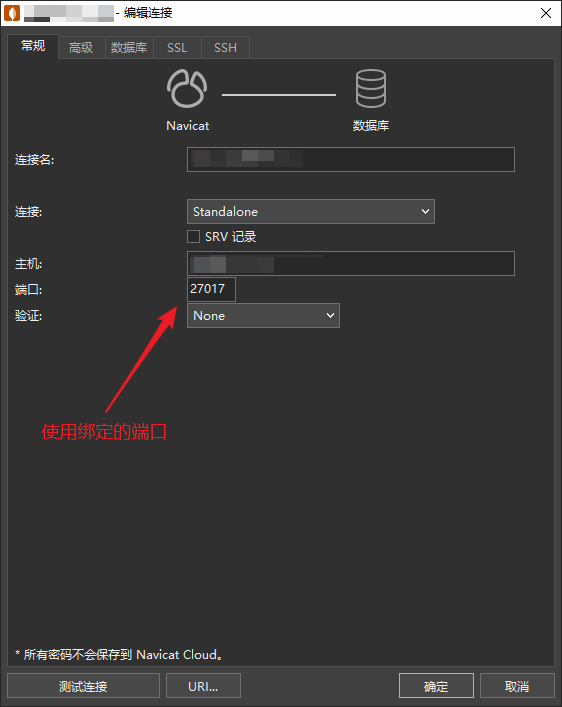
MongoDB【部署 01】mongodb最新版本6.0.5安装部署配置使用及mongodb-shell1.8.0安装使用(云盘分享安装文件)
云盘分享文件: 链接:https://pan.baidu.com/s/11sbj1QgogYHPM4udwoB1rA 提取码:l2wz 1.mongodb简单介绍 MongoDB的 官网 内容还是挺丰富的。 是由 C语言编写的,是一个基于分布式文件存储的开源数据库系统。在高负载的情况下&…...

算法竞赛必考算法——动态规划(01背包和完全背包)
动态规划(一) 目录动态规划(一)1.01背包问题1.1题目介绍1.2思路一介绍(二维数组)1.3思路二介绍(一维数组) 空间优化1.4思路三介绍(输入数据优化)2.完全背包问题2.1题目描述:2.2思路一(朴素算法)2.3思路二(将k优化处理掉)2.4思路三(优化j的初始条件)总结1.01背包问题…...
基于深度学习的农作物叶片病害检测系统(UI界面+YOLOv5+训练数据集)
摘要:农作物叶片病害检测系统用于智能检测常见农作物叶片病害情况,自动化标注、记录和保存病害位置和类型,辅助作物病害防治以增加产值。本文详细介绍基于YOLOv5深度学习模型的农作物叶片病害检测系统,在介绍算法原理的同时&#…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

Linux nano命令的基本使用
参考资料 GNU nanoを使いこなすnano基础 目录 一. 简介二. 文件打开2.1 普通方式打开文件2.2 只读方式打开文件 三. 文件查看3.1 打开文件时,显示行号3.2 翻页查看 四. 文件编辑4.1 Ctrl K 复制 和 Ctrl U 粘贴4.2 Alt/Esc U 撤回 五. 文件保存与退出5.1 Ctrl …...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...

CVPR2025重磅突破:AnomalyAny框架实现单样本生成逼真异常数据,破解视觉检测瓶颈!
本文介绍了一种名为AnomalyAny的创新框架,该方法利用Stable Diffusion的强大生成能力,仅需单个正常样本和文本描述,即可生成逼真且多样化的异常样本,有效解决了视觉异常检测中异常样本稀缺的难题,为工业质检、医疗影像…...

OCR MLLM Evaluation
为什么需要评测体系?——背景与矛盾 能干的事: 看清楚发票、身份证上的字(准确率>90%),速度飞快(眨眼间完成)。干不了的事: 碰到复杂表格(合并单元…...

算法250609 高精度
加法 #include<stdio.h> #include<iostream> #include<string.h> #include<math.h> #include<algorithm> using namespace std; char input1[205]; char input2[205]; int main(){while(scanf("%s%s",input1,input2)!EOF){int a[205]…...
