代码随想录算法训练营第三十天 | 332.重新安排行程 51. N皇后 37. 解数独 总结
打卡第30天,回溯算法第二刷。
今日任务
- 332.重新安排行程
- 51.N皇后
- 37.解数独
- 总结
332.重新安排行程
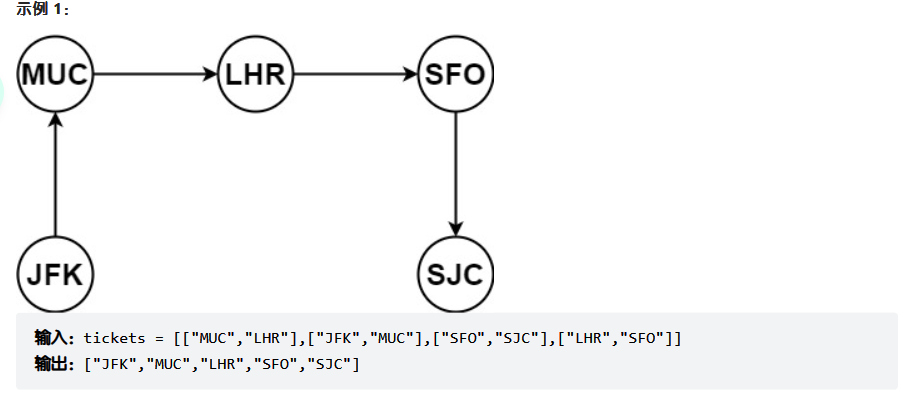
给你一份航线列表 tickets ,其中 tickets[i] = [fromi, toi] 表示飞机出发和降落的机场地点。请你对该行程进行重新规划排序。
所有这些机票都属于一个从 JFK(肯尼迪国际机场)出发的先生,所以该行程必须从 JFK 开始。如果存在多种有效的行程,请你按字典排序返回最小的行程组合。
例如,行程 [“JFK”, “LGA”] 与 [“JFK”, “LGB”] 相比就更小,排序更靠前。
假定所有机票至少存在一种合理的行程。且所有的机票 必须都用一次 且 只能用一次。

代码随想录
class Solution {
public:unordered_map<string, map<string, int>> targets;bool backtracking(int ticketNum, vector<string>& res) {if(res.size() == ticketNum + 1) return true;for(pair<const string, int>& target : targets[res[res.size() - 1]]) {if(target.second > 0) {res.push_back(target.first);target.second--;if (backtracking(ticketNum, res)) return true;target.second++;res.pop_back();}}return false;}vector<string> findItinerary(vector<vector<string>>& tickets) {targets.clear();vector<string> res;for(const vector<string>& vec: tickets) {targets[vec[0]][vec[1]]++;}res.push_back("JFK");backtracking(tickets.size(), res);return res;}
};
51.N皇后
按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。
n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n ,返回所有不同的 n 皇后问题 的解决方案。
每一种解法包含一个不同的 n 皇后问题 的棋子放置方案,该方案中 ‘Q’ 和 ‘.’ 分别代表了皇后和空位。
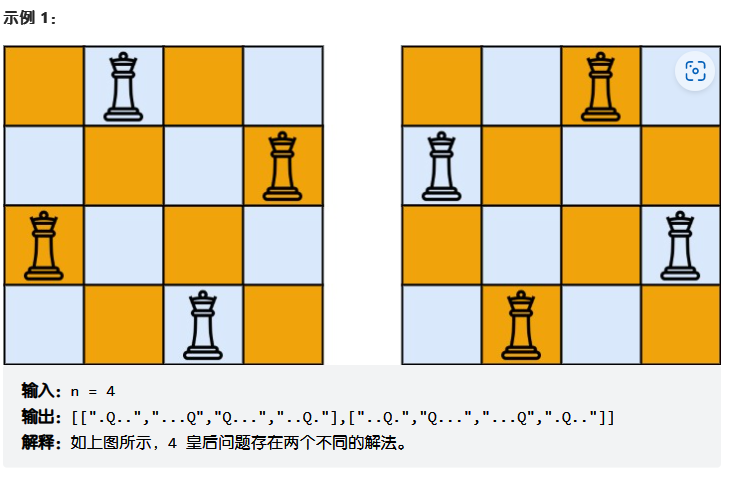

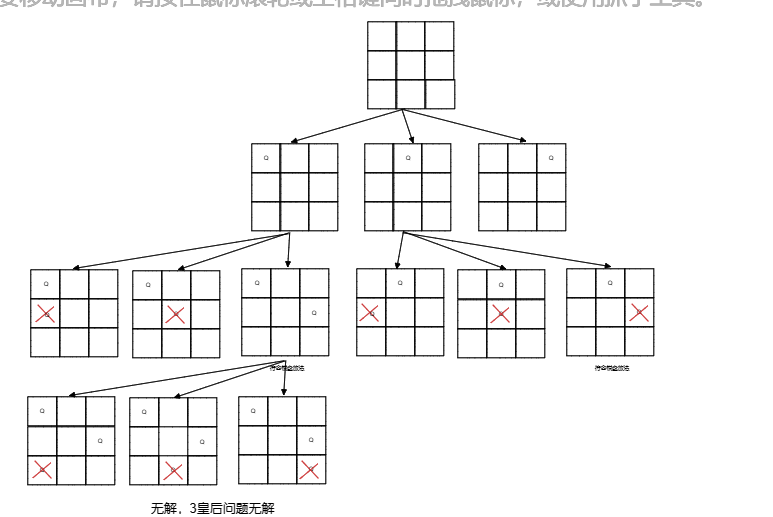
代码随想录
class Solution {
public:vector<vector<string>> res;bool isVaild(int row, int col,int n, vector<string>& chessborad) {for(int i = 0; i < row; i++) {if(chessborad[i][col] == 'Q') return false;}for(int i = row - 1, j = col - 1; i >= 0 && j >= 0; i--, j--) {if(chessborad[i][j] == 'Q') return false;}for(int i = row - 1, j = col + 1; i >= 0 && j < n; i--, j++) {if(chessborad[i][j] == 'Q') return false;}return true;}void backtarcking(int n, int row, vector<string>& chessborad) {if(row == n) {res.push_back(chessborad);return;}for(int col = 0; col < n; col++) {if(isVaild(row, col, n, chessborad)) {chessborad[row][col] = 'Q';backtarcking(n, row + 1, chessborad);chessborad[row][col] = '.';}}}vector<vector<string>> solveNQueens(int n) {res.clear();vector<string> chessborad(n, string(n, '.'));backtarcking(n, 0, chessborad);return res;}
};
37.解数独
编写一个程序,通过填充空格来解决数独问题。
数独的解法需 遵循如下规则:
数字 1-9 在每一行只能出现一次。
数字 1-9 在每一列只能出现一次。
数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。(请参考示例图)
数独部分空格内已填入了数字,空白格用 ‘.’ 表示。


代码随想录
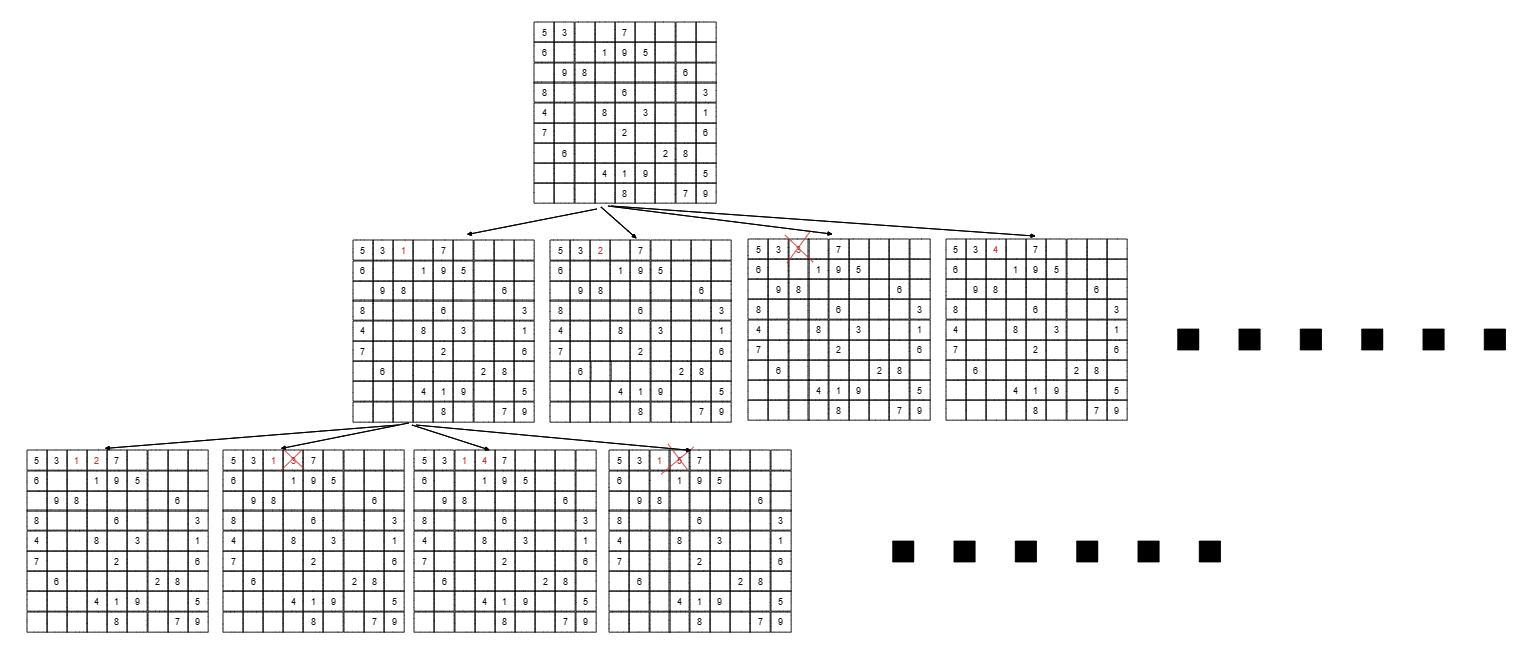
一个for循环遍历棋盘的行,一个for循环遍历棋盘的列,一行一列确定下来之后,递归遍历这个位置放9个数字的可能性!
class Solution {
public:bool backtracking(vector<vector<char>>& board) {for(int i = 0; i < board.size(); i++) {for(int j = 0; j < board.size(); j++) {if(board[i][j] != '.') continue;for(char c = '1'; c <= '9'; c++) {if(isValid(board, i, j, c)) {board[i][j] = c;if(backtracking(board)) return true;board[i][j] = '.';}}return false;}}return true;}bool isValid(vector<vector<char>>& board, int row, int col, char c) {for(int i = 0; i < 9; i++) {if(board[row][i] == c) return false;}for(int i = 0; i < 9; i++) {if(board[i][col] == c) return false;}for(int i = row - (row % 3); i < row - (row % 3) + 3; i++) {for(int j = col - (col % 3); j < col - (col % 3) + 3; j++) {if(board[i][j] == c) return false;}}return true;}void solveSudoku(vector<vector<char>>& board) {backtracking(board);}
};
相关文章:

代码随想录算法训练营第三十天 | 332.重新安排行程 51. N皇后 37. 解数独 总结
打卡第30天,回溯算法第二刷。 今日任务 332.重新安排行程51.N皇后37.解数独总结 332.重新安排行程 给你一份航线列表 tickets ,其中 tickets[i] [fromi, toi] 表示飞机出发和降落的机场地点。请你对该行程进行重新规划排序。 所有这些机票都属于一个从…...
Windows权限提升—MySQL数据库提权
Windows权限提升—MySQL数据库提权1. 前言2. 数据库提权介绍2.1. 常见数据库端口2.2. MySQL数据库提权条件2.3. MySQL数据库提权类型3. MySQL中UDF提权3.1. UDF提权介绍3.2. UDF提权思路3.3. UDF提权步骤3.3.1. 获取外连数据库3.3.1.1. 外连数据库3.3.1.2. 连接数据库3.3.1.3. …...

使用旧电脑玩Linux
今天给大家讲讲使用旧电脑玩Linux,大家应该都知道旧电脑的硬件一般比较落后,特别是一些非常老的电脑,目前还在使用的是机械硬盘,如是要跑windows可想而知,但是Linux系统对硬件性能的要求可比windows低的多了࿰…...
)
Linux安装EMQX(简洁版)
安装目录 mkdir /opt/emqx && cd /opt/emqx 安装包下载 yum -y install wget && wget https://www.emqx.com/zh/downloads/broker/5.0.20/emqx-5.0.20-el7-amd64.tar.gz 注意:https://www.emqx.com/zh/downloads/broker获取下载链接并替换(后缀&…...
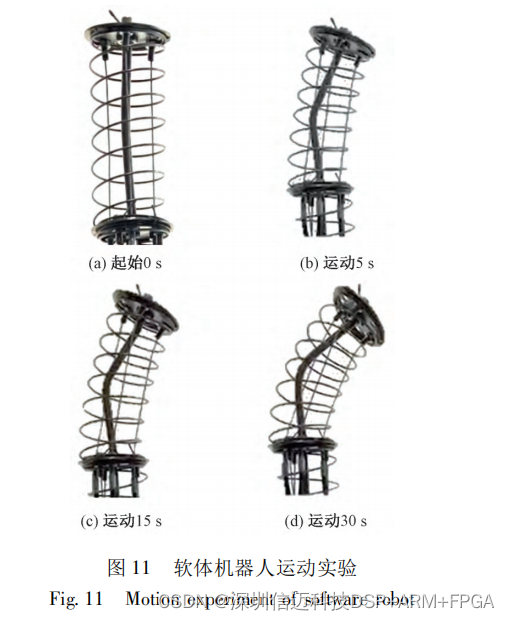
基于STM32 + FPGA 的软体机器人的 CAN总线运动控制器的设计
针对在软体机器人控制时,多电机协同控制过程中难度大、通用性差、协同性差等缺点,设计了基于 ARM和 FPGA的软体机器人的控制器局域网络 ( controller area network,CAN) 总线运动控制器,采用 ARMCortex-M4 …...
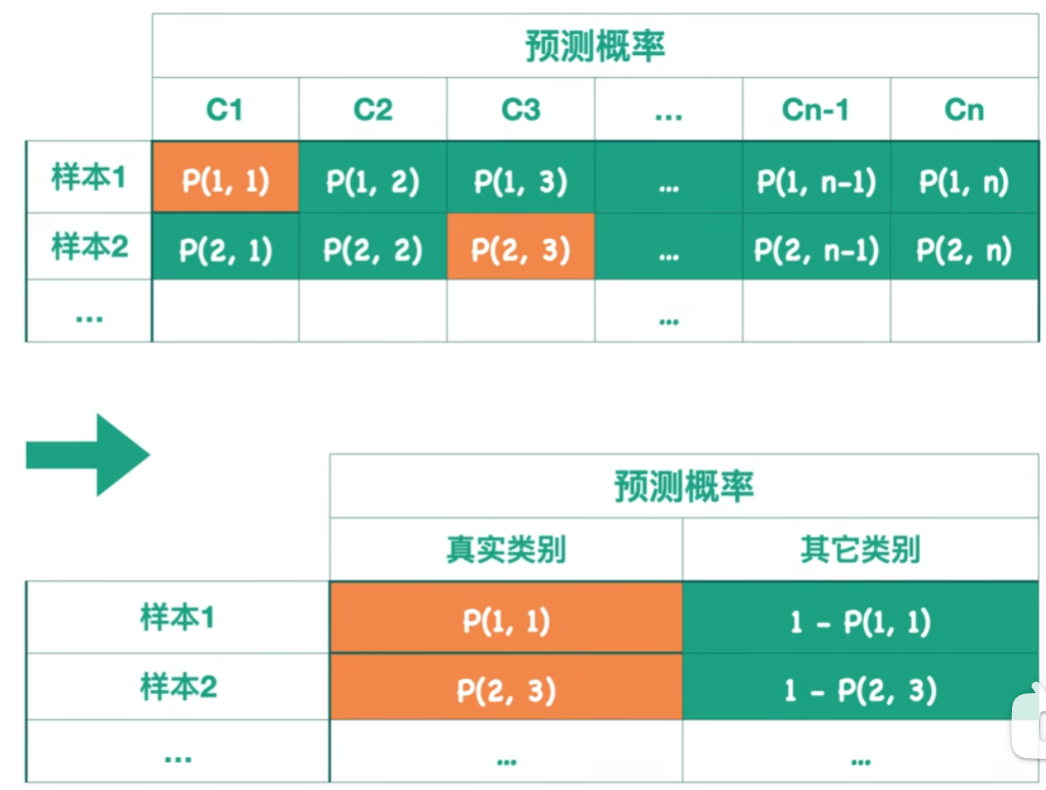
ROC曲线和AUC值
ROC曲线(Receiver Operating Characteristic,受试者工作特征)评价分类模型的可视化工具,是一条横纵坐标都限制在0-1范围内的曲线横坐标是假正率FPR,错误地判断为正例的概率纵坐标是真正率TPR,正确地判断为正…...

【vue.js】在网页中实现一个金属抛光质感的按钮
文章目录前言效果电脑效果手机效果说明完整代码index.html前言 诶?这有一个按钮(~ ̄▽ ̄)~,这是一个在html中实现的具有金属质感并且能镜面反射的按钮~ 效果 电脑效果 手机效果 说明 主要思路是使用 navig…...
android实现评论区功能
效果 activity_detail.xml <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas.android.com/apk/res/android"xmlns:app"http://schemas.android.com/apk/res-auto"xmlns:tools"http…...

Java每日一练(20230319)
目录 1. 最大矩形 🌟🌟🌟 2. 回文对 🌟🌟🌟 3. 给表达式添加运算符 🌟🌟🌟 🌟 每日一练刷题专栏 🌟 Golang每日一练 专栏 Python每日一练…...
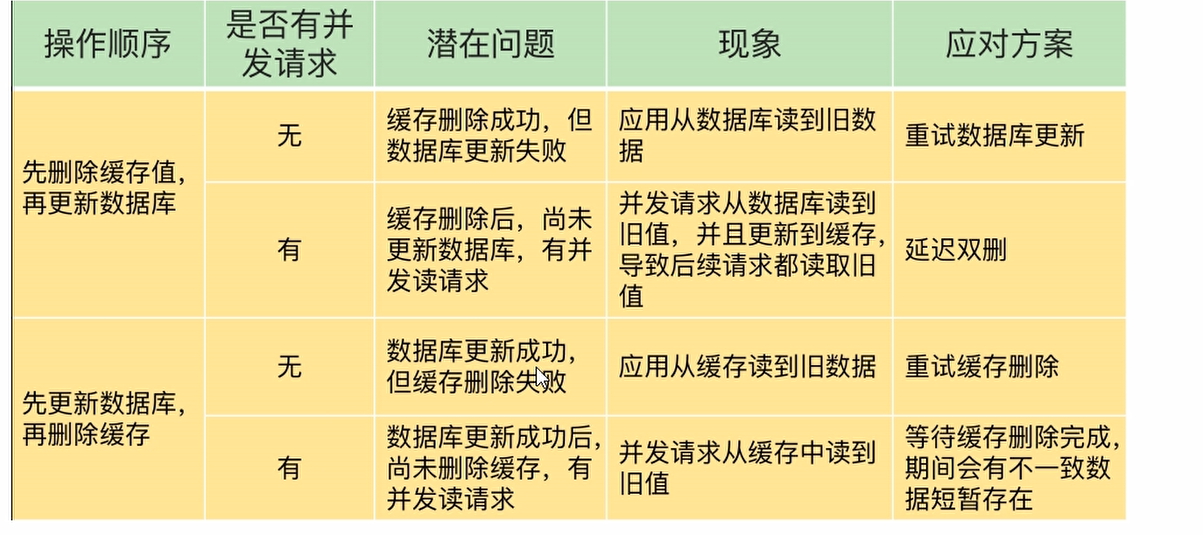
Redis缓存双写一致性
目录双写一致性Redis与Mysql双写一致性canal配置流程代码案例双写一致性理解缓存操作细分缓存一致性多种更新策略挂牌报错,凌晨升级先更新数据库,在更新缓存先删除缓存,在更新数据库先更新数据库,在删除缓存延迟双删策略总结双写一致性 Redis与Mysql双写一致性 canal 主要是…...
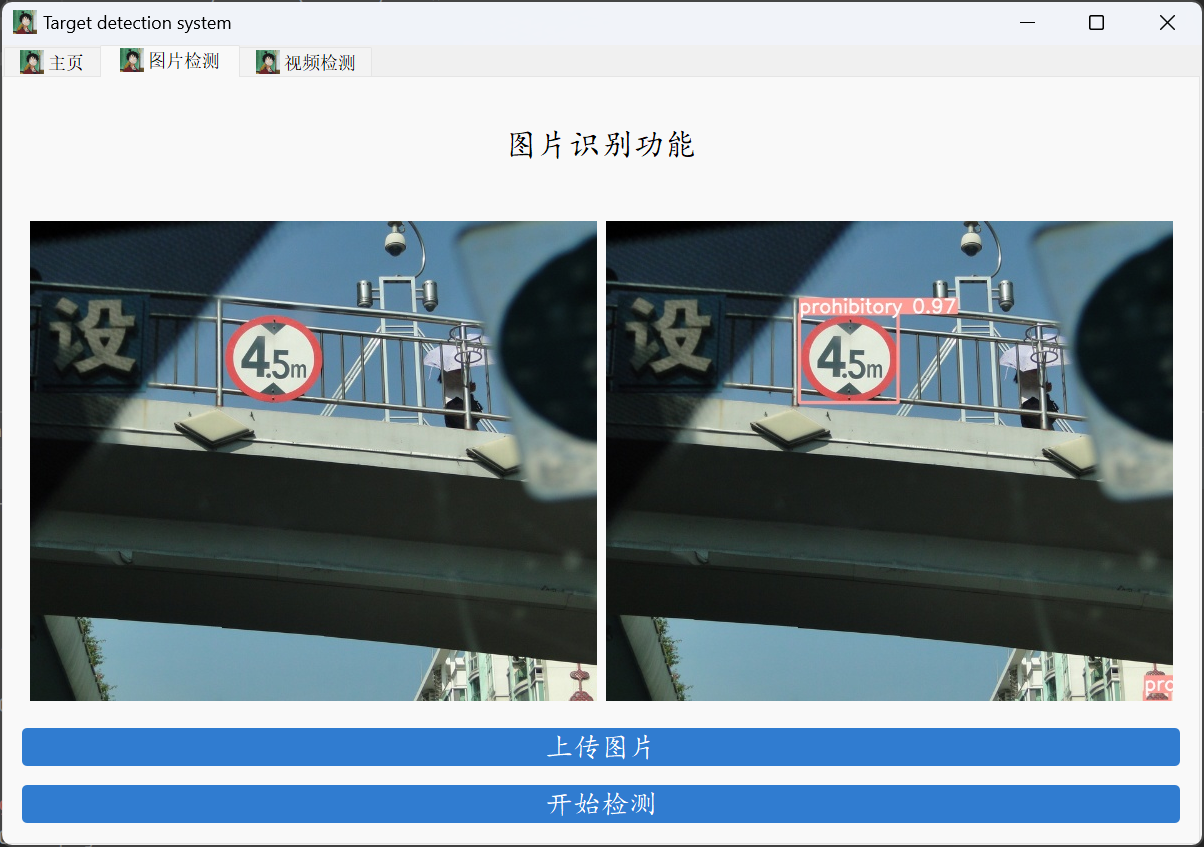
【2023-Pytorch-检测教程】手把手教你使用YOLOV5做交通标志检测
项目下载地址:YOLOV5交通标志识别检测数据集代码模型教学视频-深度学习文档类资源-CSDN文库 交通标志的目标检测算法在计算机视觉领域一直属于热点研究问题,改进的优化算法不断地被提出。国内外许多学者针对现有的目标检测方法中网络结构、目标定位、损…...
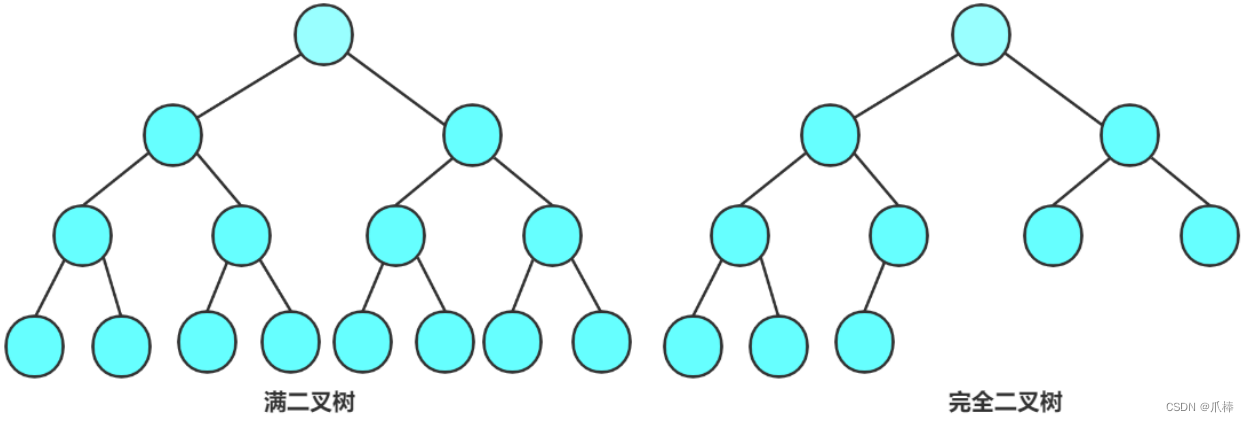
Java中的二叉树
文章目录前言一、树形结构(了解)1.1 概念1.2 概念(重要)1.3 树的表示形式(了解)1.4 树的应用二、二叉树(重点)2.1 概念2.2 两种特殊的二叉树2.3 二叉树的性质2.5 二叉树的存储2.5 二…...
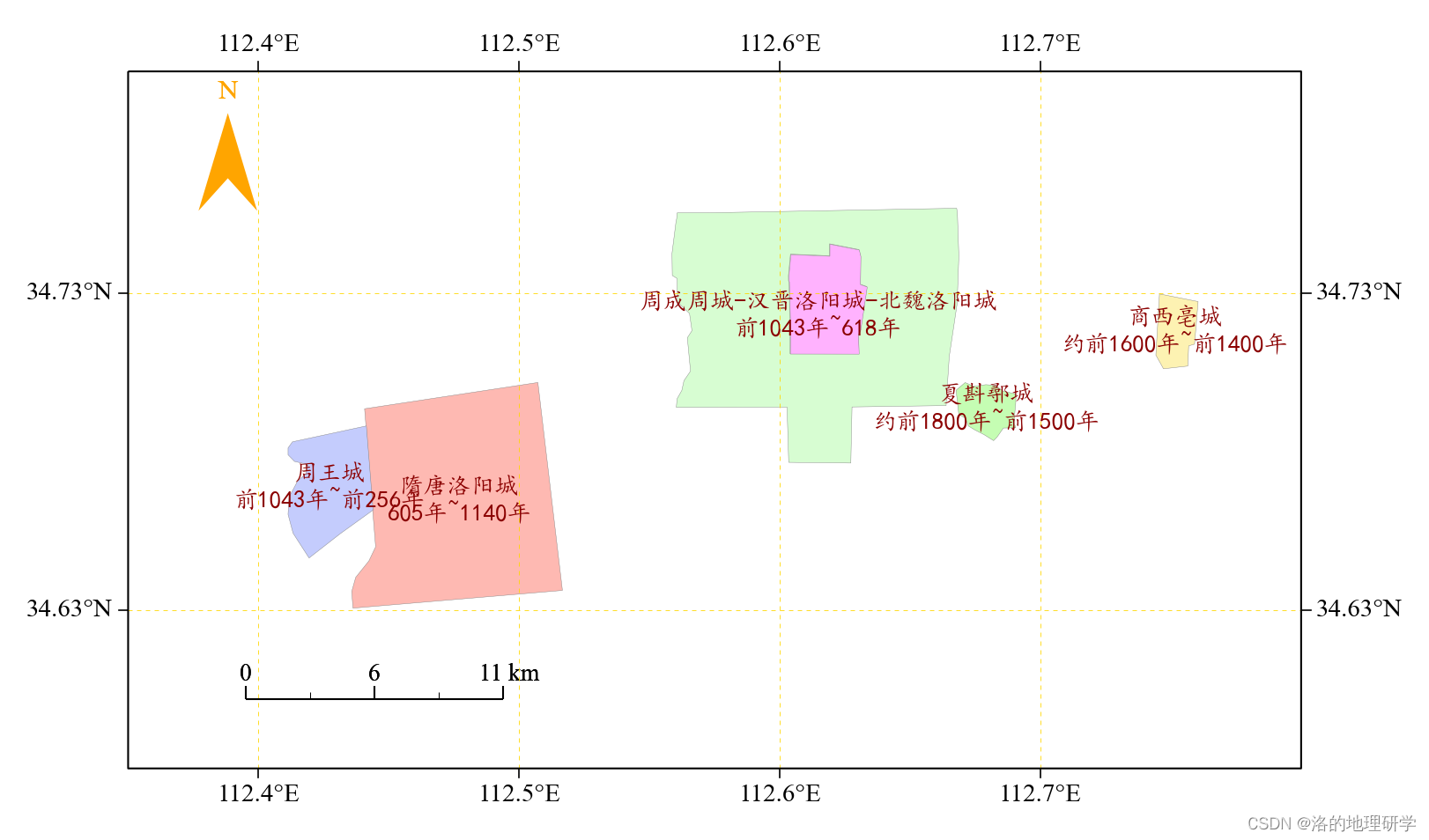
基于 gma 绘制古代洛阳 5 大都城遗址空间分布地图
了解 gma gma 是什么? gma 是一个基于 Python 的地理、气象数据快速处理和数据分析函数包(Geographic and Meteorological Analysis,gma)。gma 网站:地理与气象分析库。 gma 的主要功能有哪些? 气候气象&a…...
分析 Spring 的依赖注入模式
一、依赖注入二、Field Injection优点缺点三、Constructor Injection优点1. 容易发现 code smell优点2. 容易厘清依赖关系优点3. 容易写单元测试优点4. Immutable Object缺点:循环依赖四、总结一、依赖注入 依赖注入 (Dependency Injection,…...
IntelliJ IDEA创建Servlet
目录 ——————————————————————————————— 一、创建Java项目 1、创建java项目 2、选择java 3、next 4、给项目命名 5、新创建完java项目的目录结构 二、变java为servlet项目 1、变servlet项目 2、选择Web Application 3、更新完成后的目录…...

Spring Boot如何让自己的bean优先加载
背景介绍 在一些需求中,可能存在某些场景,比如先加载自己的bean,然后自己的bean做一些DB操作,初始化配置问题,然后后面的bean基于这个配置文件,继续做其他的业务逻辑。因此有了本文的这个题目。 实现方法…...
LeetCode分类刷题----动态规划
动态规划509.斐波那契数列70.爬楼梯746.使用最小花费怕楼梯62.不同路径63.不同路径||343.整数拆分96.不同的二叉搜索树01背包问题416.分割等和子集1049.最后一块石头的重量||494.目标和474.一和零完全背包问题518.零钱兑换||377.组合总和IV322.零钱兑换279.完全平方数139.单词拆…...

今年好像没有金三银四了?
大家好,我是记得诚。 金三银四,是换工作的高峰期,新的一年结束了,在年前拿完年终奖,在年后3月和4月换个满意的工作。 单从我公司来看,目前还没有一个人离职,往年离职率是要高一些的。 还有我…...
【C++】入门知识之 函数重载
前言提到重载这个词,我们会想到什么呢?重载有一种一词多义的意思,中华文化博大精深,之前有一个笑话,中国的乒乓球谁都打不过,男足谁都打不过,哈哈哈这也是非常有意思的,但是今天我们…...
文心一言发布,你怎么看?chatGPT
百度全新一代知识增强大语言模型“文心一言”于2021年3月16日正式发布,作为一款自然语言处理技术,它引起了广泛的关注和讨论。 首先,文心一言是一款具有重大意义的自然语言处理技术。在人工智能领域,自然语言处理技术一直是一个难…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

比较数据迁移后MySQL数据库和OceanBase数据仓库中的表
设计一个MySQL数据库和OceanBase数据仓库的表数据比较的详细程序流程,两张表是相同的结构,都有整型主键id字段,需要每次从数据库分批取得2000条数据,用于比较,比较操作的同时可以再取2000条数据,等上一次比较完成之后,开始比较,直到比较完所有的数据。比较操作需要比较…...

消防一体化安全管控平台:构建消防“一张图”和APP统一管理
在城市的某个角落,一场突如其来的火灾打破了平静。熊熊烈火迅速蔓延,滚滚浓烟弥漫开来,周围群众的生命财产安全受到严重威胁。就在这千钧一发之际,消防救援队伍迅速行动,而豪越科技消防一体化安全管控平台构建的消防“…...

从零开始了解数据采集(二十八)——制造业数字孪生
近年来,我国的工业领域正经历一场前所未有的数字化变革,从“双碳目标”到工业互联网平台的推广,国家政策和市场需求共同推动了制造业的升级。在这场变革中,数字孪生技术成为备受关注的关键工具,它不仅让企业“看见”设…...

webpack面试题
面试题:webpack介绍和简单使用 一、webpack(模块化打包工具)1. webpack是把项目当作一个整体,通过给定的一个主文件,webpack将从这个主文件开始找到你项目当中的所有依赖文件,使用loaders来处理它们&#x…...
