【蓝桥杯专题】 DP(C++ | 洛谷 | acwing | 蓝桥)
菜狗现在才开始备战蓝桥杯QAQ
文章目录
- 【蓝桥杯专题】 DP(C++ | 洛谷 | acwing | 蓝桥)
- AcWing 1205. 买不到的数目
- Acwing 1216. 饮料换购【模拟】
- 01背包
- 271. 杨老师的照相排列
- 最长公共上升子序列
- P
- P
- P
- P
- P
- P
- P
- P
- 总结

【蓝桥杯专题】 DP(C++ | 洛谷 | acwing | 蓝桥)
- 看最后总结!!
AcWing 1205. 买不到的数目
链接 链接
- 思路 暴力打表 找规律
#include <iostream>
using namespace std;int main () {int p, q;cin >> p >> q;cout << ((p - 1) * (q - 1) - 1) << endl;return 0;
} Acwing 1216. 饮料换购【模拟】
链接 链接
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;int main()
{int n, ans ;cin >> n; ans = n;while((n / 3) >= 1) {// cout <<n <<endl;int t = n / 3;ans += t;n %= 3 ;n += t;}cout << ans << endl;
}
01背包
链接 链接

#include <bits/stdc++.h>
// #include <iostream>
using namespace std;
typedef long long ll;
typedef double db;
#define rep(i, a, n) for(int i = a; i <= n; i ++)
#define per(i, a, n) for(int i = n; i <= a; i --)
#define pb push_back;
#define fs first;
#define sz second;
#include <stdlib.h> // atoi
#define debug cout<<"debug"<<"\n"
#define endl "\n";
const int INF = 0x3f3f3f3f;
const int mod=1e9+7;
const int N = 1010;int w[N], v[N];
int f[N][N];void solve () {int N, V;ll ans = 0;cin >> N >> V;rep(i, 1, N) {cin >> v[i] >> w[i];}
// 当前背包容量不够(j < v[i]),没得选,因此前 i 个物品最优解即为前 i−1个物品最优解:f[i][j] = f[i - 1][j]。
// 如果可以选 :f[i][j] = f[i - 1][j - v[i]] + w[i]。rep(i, 1, N) { rep(j, 1, V) {if(j < v[i]) f[i][j] = f[i - 1][j];else f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i]] + w[i]);}}cout << f[N][V] << endl;
}int main(void){freopen("in.txt","r",stdin);ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);int T = 1;// cin >> T;while(T --) solve();return 0;
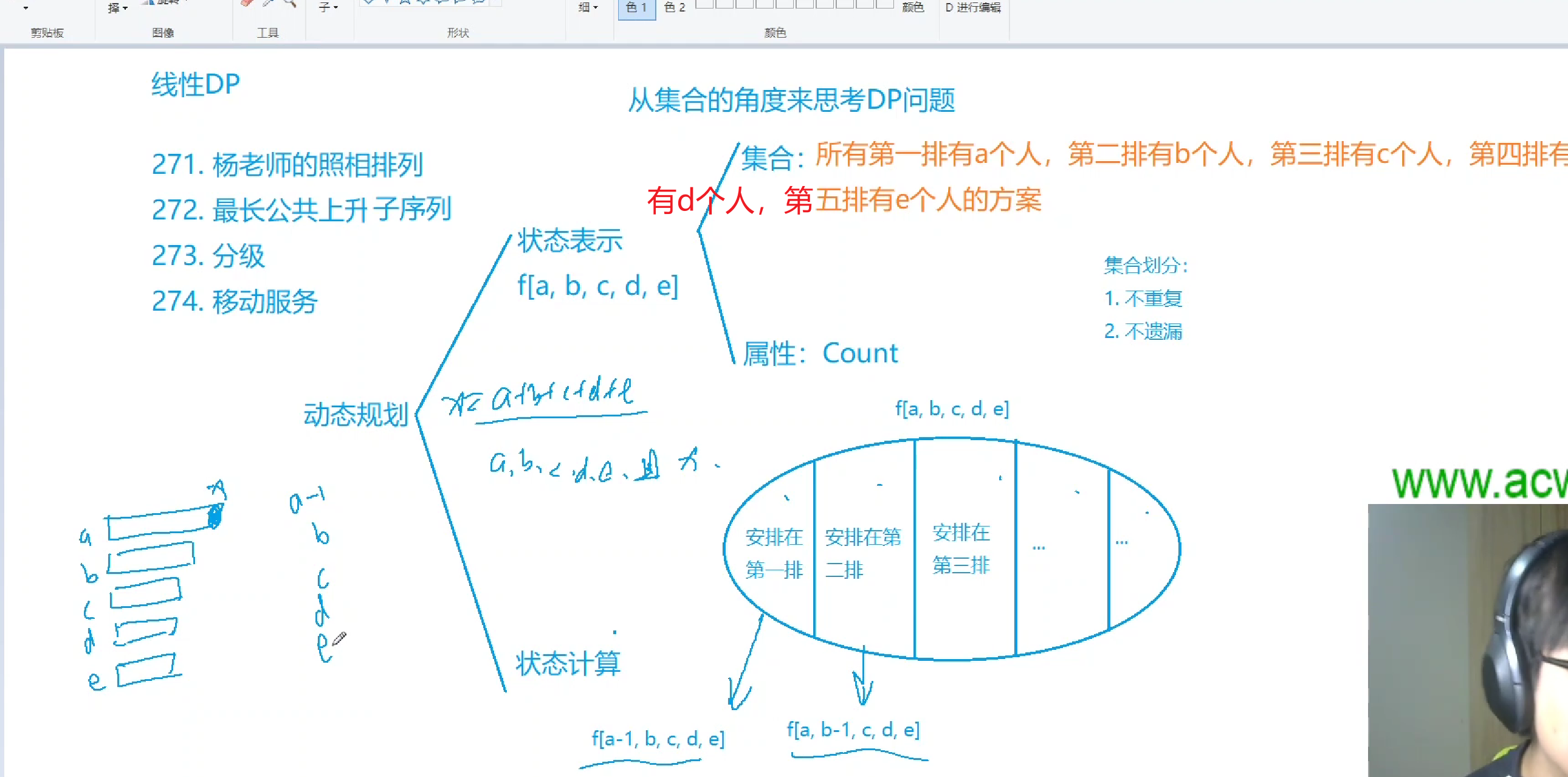
}271. 杨老师的照相排列
链接 链接
#include <bits/stdc++.h>
// #include <iostream>
using namespace std;
typedef long long ll;
typedef double db;
#define rep(i, a, n) for(int i = a; i <= n; i ++)
#define per(i, a, n) for(int i = n; i <= a; i --)
#define pb push_back;
#define fs first;
#define sz second;
#include <stdlib.h> // atoi
#define debug cout<<"debug"<<"\n"
#define endl "\n";
const int INF = 0x3f3f3f3f;
const int mod=1e9+7;
const int N = 31;ll f[N][N][N][N][N];void solve () {int n;while(cin >> n , n) {int s[5] = {0};rep(i, 0, n - 1) cin >> s[i];memset(f, 0 , sizeof f);f[0][0][0][0][0] = 1; rep(a, 0, s[0]) {rep(b, 0, min(s[1], a)) {rep(c, 0, min(s[2], b)) {rep(d, 0, min(s[3], c)) {rep(e, 0, min(s[4], d)) {// f[a][b][c][d][e]代表从后往前每排人数分别为a, b, c, d, e的所有方案的集合, 其中a >= b >= c >= d >= e; 逆序的
// f[a][b][c][d][e]的值是该集合中元素的数量;ll &x = f[a][b][c][d][e];if (a && a - 1 >= b) x += f[a - 1][b][c][d][e];if (b && b - 1 >= c) x += f[a][b - 1][c][d][e];if (c && c - 1 >= d) x += f[a][b][c - 1][d][e];if (d && d - 1 >= e) x += f[a][b][c][d - 1][e];if (e) x += f[a][b][c][d][e - 1];// 当a > 0 && a - 1 >= b时,最后一个同学可能被安排在第1排,方案数是f[a - 1][b][c][d][e];
// 当b > 0 && b - 1 >= c时,最后一个同学可能被安排在第2排,方案数是f[a][b - 1][c][d][e];
// 当c > 0 && c - 1 >= d时,最后一个同学可能被安排在第3排,方案数是f[a][b][c - 1][d][e];
// 当d > 0 && d - 1 >= e时,最后一个同学可能被安排在第4排,方案数是f[a][b][c][d - 1][e];
// 当e > 0时,最后一个同学可能被安排在第5排,方案数是f[a][b][c][d][e - 1];} }}}}cout << f[s[0]][s[1]][s[2]][s[3]][s[4]] << endl;}}int main(void){freopen("in.txt","r",stdin);ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);int T = 1;// cin >> T;while(T --) solve();return 0;
}
最长公共上升子序列
链接 链接
#include <bits/stdc++.h>
// #include <iostream>
using namespace std;
typedef long long ll;
typedef double db;
#define rep(i, a, n) for(int i = a; i <= n; i ++)
#define per(i, a, n) for(int i = n; i <= a; i --)
#define pb push_back;
#define fs first;
#define sz second;
#include <stdlib.h> // atoi
#define debug cout<<"debug"<<"\n"
#define endl "\n";
const int INF = 0x3f3f3f3f;
const int mod=1e9+7;
const int N = 3111;int a[N], b[N];
int f[N][N];void solve () {int n ;cin >> n;rep(i, 1, n) cin>> a[i];rep(i, 1, n) cin>> b[i];//版本1// rep(i, 1, n) {// rep(j, 1 , n) {// f[i][j] = f[i - 1][j];// if(a[i] == b[j]) {// // int maxv = 1; // O(n^ 3)// // for(int k =1; k < j; k ++) {// // if(b[j] > b[k]) {// // maxv = max(maxv, f[i - 1][k] + 1);// // }// // f[i][j] = max(maxv, f[i][j]);// // }// }// }// }//版本2: rep(i, 1, n) {int maxv = 1;rep(j, 1, n) {f[i][j] = f[i - 1][j];if(a[i] == b[j] ) f[i][j] = max(maxv, f[i][j]);if(a[i] > b[j]) maxv = max(maxv, f[i - 1][j] + 1);}}int res = 0;rep(i, 1, n) {res = max(res, f[n][i]);}cout << res << endl;}int main(void){freopen("in.txt","r",stdin);ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);int T = 1;// cin >> T;while(T --) solve();return 0;
}
# P
[链接 链接]( )
P
链接 链接
P
链接 链接
P
链接 链接
P
链接 链接
P
链接 链接
P
链接 链接
P
链接 链接
P
链接 链接
总结
- 数论别浪费太多时间, 做法暴力打表找规律 , 能做出来就做
- exit(0) 调试bug 针对没有输出的时候好用
- DP 多刷 (大部分题型)

相关文章:

【蓝桥杯专题】 DP(C++ | 洛谷 | acwing | 蓝桥)
菜狗现在才开始备战蓝桥杯QAQ 文章目录【蓝桥杯专题】 DP(C | 洛谷 | acwing | 蓝桥)AcWing 1205. 买不到的数目Acwing 1216. 饮料换购【模拟】01背包271. 杨老师的照相排列最长公共上升子序列PPPPPPPP总结【蓝桥杯专题】 DP(C | 洛谷 | acwi…...

咪咕MGV3201_ZG_GK国科6323_UWE5621DS_免拆卡刷固件包
咪咕MGV3201_ZG_GK国科6323_UWE5621DS_免拆卡刷固件包 特点: 1、适用于对应型号的电视盒子刷机; 2、开放原厂固件屏蔽的市场安装和u盘安装apk; 3、修改dns,三网通用; 4、大量精简内置的没用的软件,运行…...

重构数据-Change Value to Reference将实值对象改为引用对象三
重构数据-Change Value to Reference将实值对象改为引用对象三 1.将实值对象改为引用对象 1.1.实值对象和引用对象区别 下面通过客户Customer和订单Order两个对象介绍下它们的区别 值对象:当一个客户Customer下了多个订单Order后,每个订单类都将创建一…...

计算机网络——通信专业面试问题学习笔记
文章目录1、计算机网络这门课学了什么?目录里有多少章?2、Internet的概念与发展史3、什么是交换?三种交换方式4、OSI的七层协议, TCP/IP的四层协议, 五层协议5、WAN 、LAN 、MAN、PAN这些能分的清楚吗?全称分别都是什么࿱…...
代码随想录算法训练营第三十天 | 332.重新安排行程 51. N皇后 37. 解数独 总结
打卡第30天,回溯算法第二刷。 今日任务 332.重新安排行程51.N皇后37.解数独总结 332.重新安排行程 给你一份航线列表 tickets ,其中 tickets[i] [fromi, toi] 表示飞机出发和降落的机场地点。请你对该行程进行重新规划排序。 所有这些机票都属于一个从…...
Windows权限提升—MySQL数据库提权
Windows权限提升—MySQL数据库提权1. 前言2. 数据库提权介绍2.1. 常见数据库端口2.2. MySQL数据库提权条件2.3. MySQL数据库提权类型3. MySQL中UDF提权3.1. UDF提权介绍3.2. UDF提权思路3.3. UDF提权步骤3.3.1. 获取外连数据库3.3.1.1. 外连数据库3.3.1.2. 连接数据库3.3.1.3. …...

使用旧电脑玩Linux
今天给大家讲讲使用旧电脑玩Linux,大家应该都知道旧电脑的硬件一般比较落后,特别是一些非常老的电脑,目前还在使用的是机械硬盘,如是要跑windows可想而知,但是Linux系统对硬件性能的要求可比windows低的多了࿰…...
)
Linux安装EMQX(简洁版)
安装目录 mkdir /opt/emqx && cd /opt/emqx 安装包下载 yum -y install wget && wget https://www.emqx.com/zh/downloads/broker/5.0.20/emqx-5.0.20-el7-amd64.tar.gz 注意:https://www.emqx.com/zh/downloads/broker获取下载链接并替换(后缀&…...
基于STM32 + FPGA 的软体机器人的 CAN总线运动控制器的设计
针对在软体机器人控制时,多电机协同控制过程中难度大、通用性差、协同性差等缺点,设计了基于 ARM和 FPGA的软体机器人的控制器局域网络 ( controller area network,CAN) 总线运动控制器,采用 ARMCortex-M4 …...
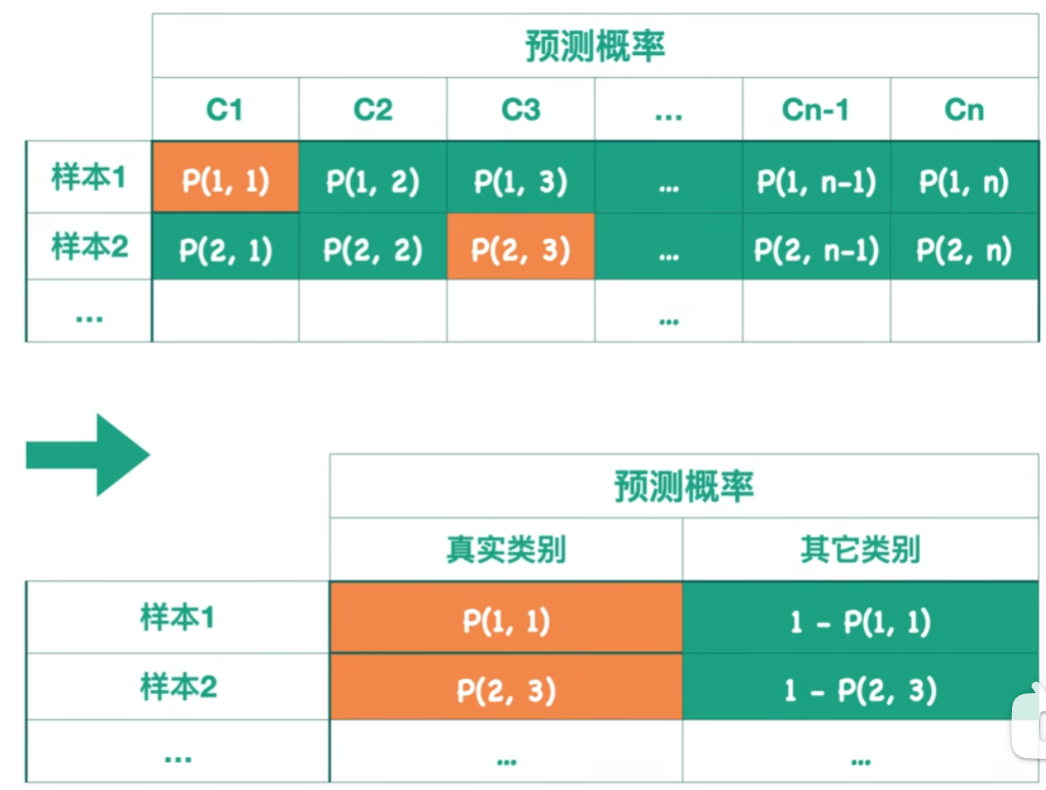
ROC曲线和AUC值
ROC曲线(Receiver Operating Characteristic,受试者工作特征)评价分类模型的可视化工具,是一条横纵坐标都限制在0-1范围内的曲线横坐标是假正率FPR,错误地判断为正例的概率纵坐标是真正率TPR,正确地判断为正…...

【vue.js】在网页中实现一个金属抛光质感的按钮
文章目录前言效果电脑效果手机效果说明完整代码index.html前言 诶?这有一个按钮(~ ̄▽ ̄)~,这是一个在html中实现的具有金属质感并且能镜面反射的按钮~ 效果 电脑效果 手机效果 说明 主要思路是使用 navig…...
android实现评论区功能
效果 activity_detail.xml <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas.android.com/apk/res/android"xmlns:app"http://schemas.android.com/apk/res-auto"xmlns:tools"http…...

Java每日一练(20230319)
目录 1. 最大矩形 🌟🌟🌟 2. 回文对 🌟🌟🌟 3. 给表达式添加运算符 🌟🌟🌟 🌟 每日一练刷题专栏 🌟 Golang每日一练 专栏 Python每日一练…...
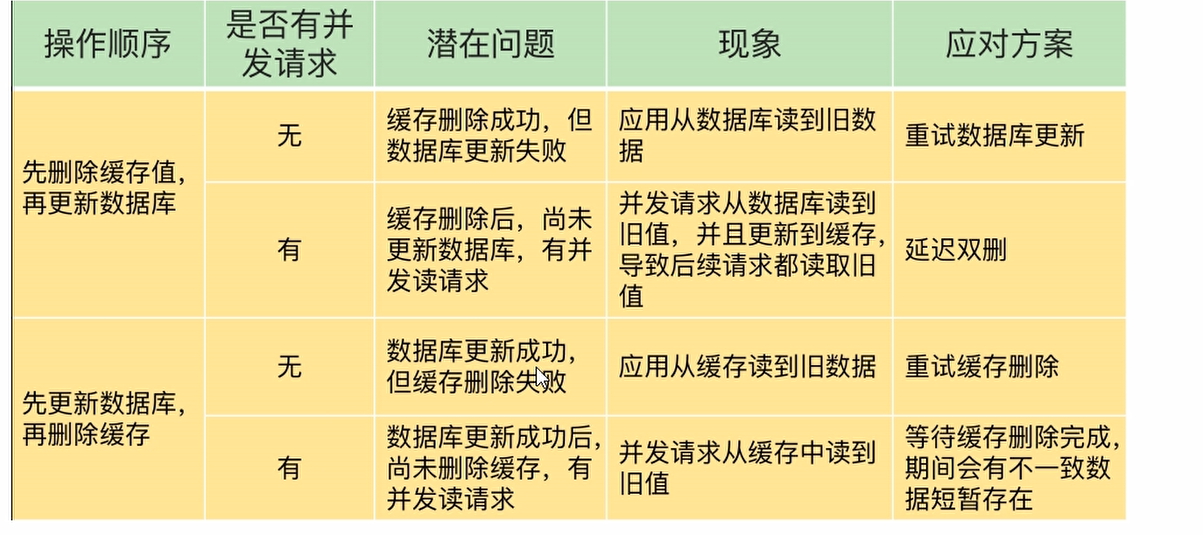
Redis缓存双写一致性
目录双写一致性Redis与Mysql双写一致性canal配置流程代码案例双写一致性理解缓存操作细分缓存一致性多种更新策略挂牌报错,凌晨升级先更新数据库,在更新缓存先删除缓存,在更新数据库先更新数据库,在删除缓存延迟双删策略总结双写一致性 Redis与Mysql双写一致性 canal 主要是…...
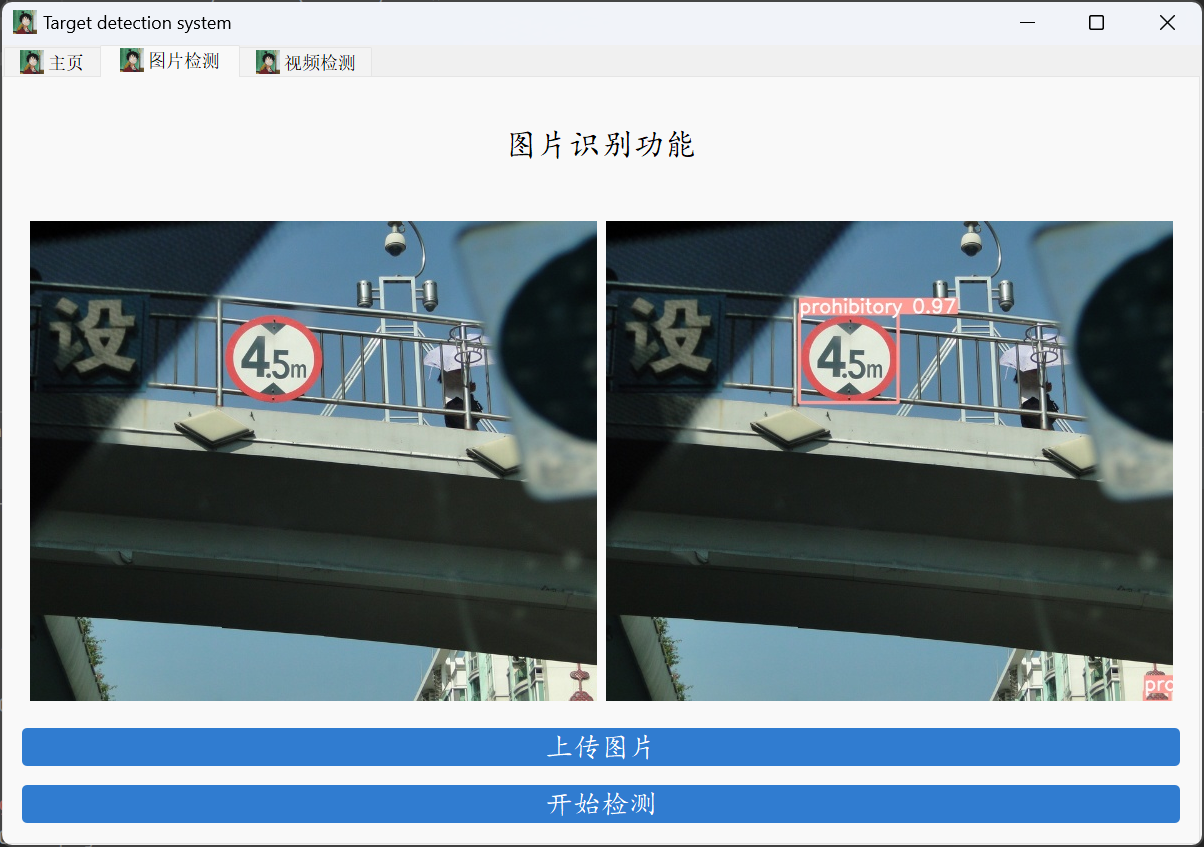
【2023-Pytorch-检测教程】手把手教你使用YOLOV5做交通标志检测
项目下载地址:YOLOV5交通标志识别检测数据集代码模型教学视频-深度学习文档类资源-CSDN文库 交通标志的目标检测算法在计算机视觉领域一直属于热点研究问题,改进的优化算法不断地被提出。国内外许多学者针对现有的目标检测方法中网络结构、目标定位、损…...
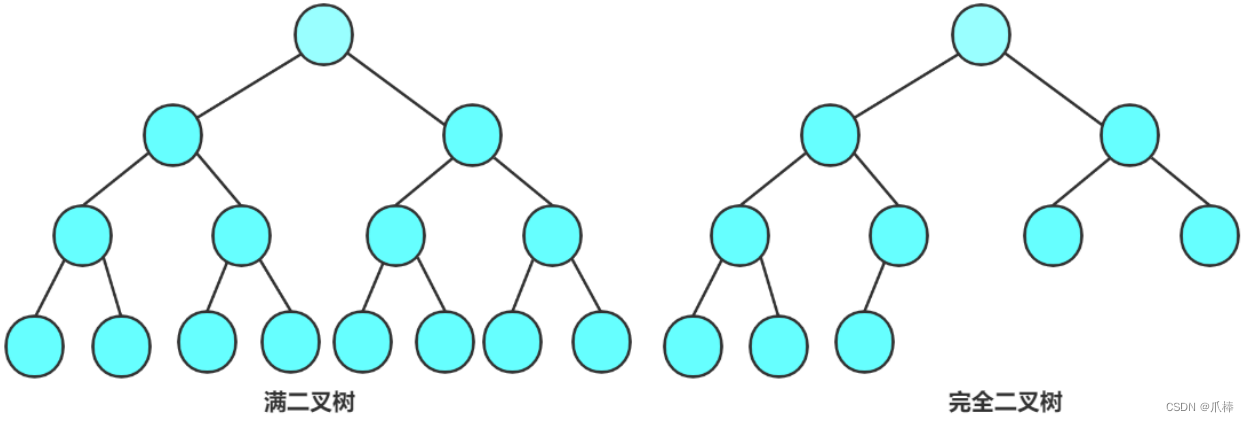
Java中的二叉树
文章目录前言一、树形结构(了解)1.1 概念1.2 概念(重要)1.3 树的表示形式(了解)1.4 树的应用二、二叉树(重点)2.1 概念2.2 两种特殊的二叉树2.3 二叉树的性质2.5 二叉树的存储2.5 二…...
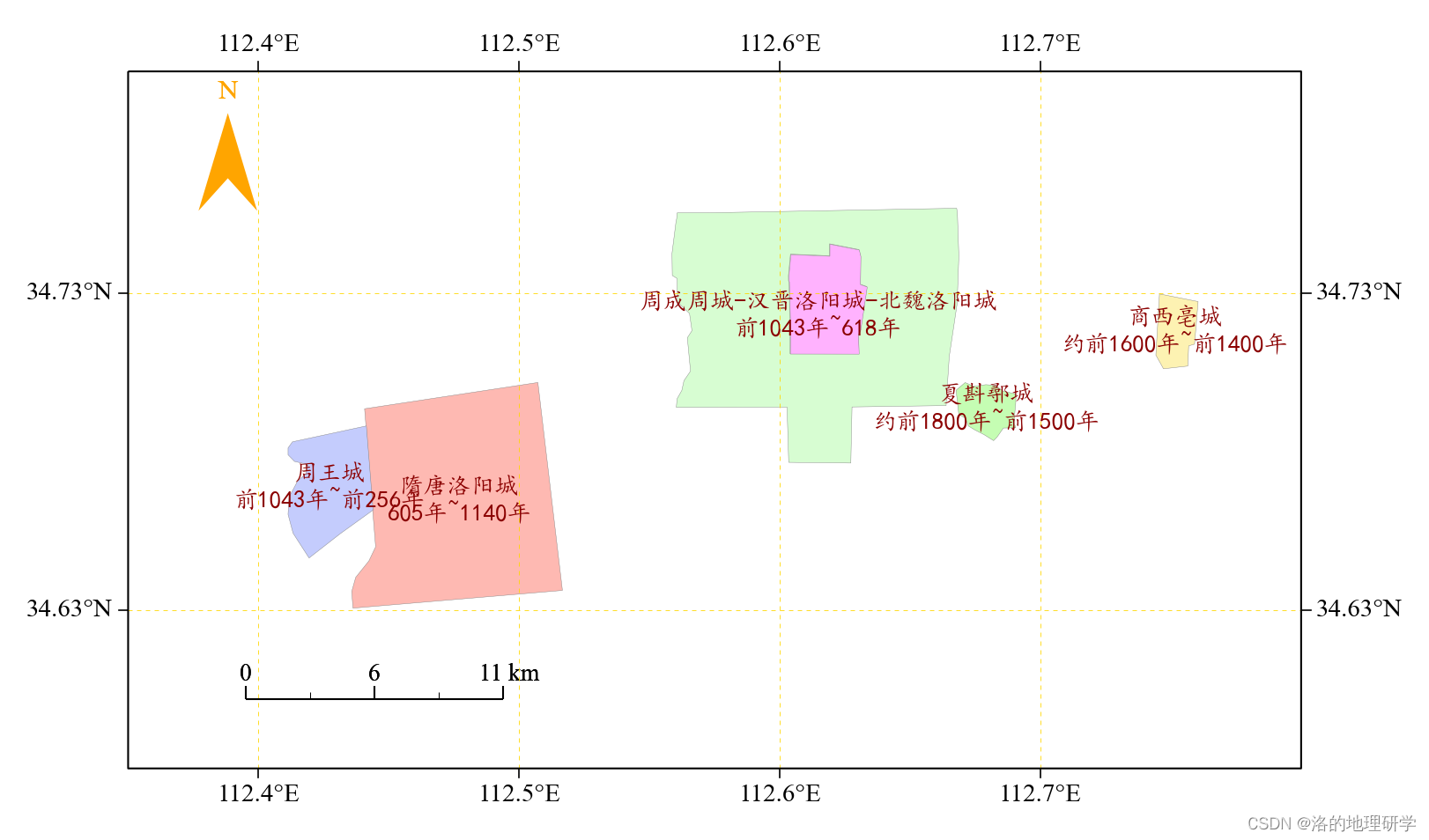
基于 gma 绘制古代洛阳 5 大都城遗址空间分布地图
了解 gma gma 是什么? gma 是一个基于 Python 的地理、气象数据快速处理和数据分析函数包(Geographic and Meteorological Analysis,gma)。gma 网站:地理与气象分析库。 gma 的主要功能有哪些? 气候气象&a…...
分析 Spring 的依赖注入模式
一、依赖注入二、Field Injection优点缺点三、Constructor Injection优点1. 容易发现 code smell优点2. 容易厘清依赖关系优点3. 容易写单元测试优点4. Immutable Object缺点:循环依赖四、总结一、依赖注入 依赖注入 (Dependency Injection,…...
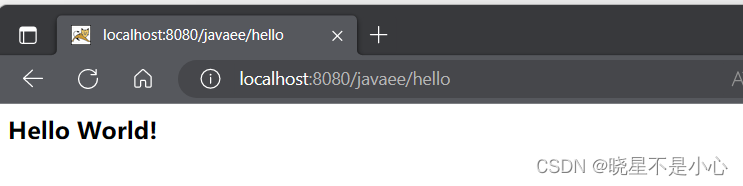
IntelliJ IDEA创建Servlet
目录 ——————————————————————————————— 一、创建Java项目 1、创建java项目 2、选择java 3、next 4、给项目命名 5、新创建完java项目的目录结构 二、变java为servlet项目 1、变servlet项目 2、选择Web Application 3、更新完成后的目录…...

Spring Boot如何让自己的bean优先加载
背景介绍 在一些需求中,可能存在某些场景,比如先加载自己的bean,然后自己的bean做一些DB操作,初始化配置问题,然后后面的bean基于这个配置文件,继续做其他的业务逻辑。因此有了本文的这个题目。 实现方法…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

JavaScript基础-API 和 Web API
在学习JavaScript的过程中,理解API(应用程序接口)和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能,使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...

WPF八大法则:告别模态窗口卡顿
⚙️ 核心问题:阻塞式模态窗口的缺陷 原始代码中ShowDialog()会阻塞UI线程,导致后续逻辑无法执行: var result modalWindow.ShowDialog(); // 线程阻塞 ProcessResult(result); // 必须等待窗口关闭根本问题:…...
HybridVLA——让单一LLM同时具备扩散和自回归动作预测能力:训练时既扩散也回归,但推理时则扩散
前言 如上一篇文章《dexcap升级版之DexWild》中的前言部分所说,在叠衣服的过程中,我会带着团队对比各种模型、方法、策略,毕竟针对各个场景始终寻找更优的解决方案,是我个人和我司「七月在线」的职责之一 且个人认为,…...

Unity VR/MR开发-VR开发与传统3D开发的差异
视频讲解链接:【XR马斯维】VR/MR开发与传统3D开发的差异【UnityVR/MR开发教程--入门】_哔哩哔哩_bilibili...
