【算法/训练】:动态规划(线性DP)
一、路径类
1. 字母收集

思路:
1、预处理
对输入的字符矩阵我们按照要求将其转换为数字分数,由于只能往下和往右走,因此走到(i,j)的位置要就是从(i - 1, j)往下走,或者是从(i,j - 1)的位置往右走,由于我们要使得路程遍历积分最多,则应该从积分多的位置过来,
2、状态表示 dp[i][j] 表示:从[0, 0]出发,到底[i, j]位置,一共有多少分
3、状态转移方程
故(i,j)位置的积分应该为dp[ i ][ j ] = max(dp[ i - 1 ][ j ], dp[ i ][ j - 1 ]) + dp[ i ][ j ];
4、初始化
但是上面仅对于(i >= 1 && j >= 1)成立,对于第一行和第一列我们应该特殊处理,利用前缀和的知识可以求得,走到第一列的第i个位置最多能拿的积分以及走到第一行的第j个位置最多能拿的积分,然后我们就可以按照dp[ i ][ j ] = max(dp[ i - 1 ][ j ], dp[ i ][ j - 1 ]) + dp[ i ][ j ]的方法遍历每个节点即可
#include <iostream>
using namespace std;const int N = 1005;
int dp[N][N];int main() {int n, m;cin >> n >> m;char ch;for (int i = 0; i < n; i++){for (int j = 0; j < m; j++){cin >> ch;if (ch == 'l') dp[i][j] = 4;else if (ch == 'o') dp[i][j] = 3;else if (ch == 'v') dp[i][j] = 2;else if (ch == 'e') dp[i][j] = 1;else a[i][j] = 0;}}for (int i = 1; i < n; i++) dp[i][0] = dp[i - 1][0] + dp[i][0];
for (int j = 1; j < m; j++) dp[0][j] = dp[0][j - 1] + dp[0][j]; for (int i = 1; i < n; i++){for (int j = 1; j < m; j++){dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]) + dp[i][j];}}cout << dp[n - 1][m - 1] << endl;return 0;
}
2、[NOIP2002 普及组] 过河卒

分析:

思路:
1、状态表示
dp[i][j] 表示:从[0, 0]出发,到底[i, j]位置,一共有多少种方法
2、状态转移方程dp[ i ][ j ] = dp[ i - 1 ][ j ] + dp[i][j - 1] (i > 0 && j > 0)
当走到马可以走的地方,dp[ i ][ j ] = 0;
3、初始化先创建一个 dp[ n + 2 ][ m + 2 ],然后让dp[ 0 ][ 1 ] = 1 或者 dp[ 1 ][ 0 ] = 1。注意这样初始化的时候,x需要+1,y也需要+1.和dp表位置一一对应
#include <iostream>
#include <vector>
using namespace std;//int dp[1005][1005];
int main()
{int n, m, x, y;cin >> n >> m >> x >> y;vector<vector<long long>> dp(n + 2, vector<long long>(m + 2));dp[0][1] = 1;x += 1, y += 1;和dp表位置一一对应for (int i = 1; i <= n + 1; i++){for (int j = 1; j <= m + 1; j++) { //马所在位置if (i != x && j != y && abs(i - x) + abs(j - y) == 3 || (i == x && j == y)){dp[i][j] == 0;}else dp[i][j] = dp[i - 1][j] + dp[i][j - 1];}}cout << dp[n + 1][m + 1] << endl;return 0;
}二、子序列和连续序列类
1. mari和shiny

🌈线性 dp
在维护 i 位置之前,⼀共有多少个 "s" "sh" ,然后更新 "shy" 的个数。
(1)状态表示
s[i]:字符串 str 中 [0, i] 区间内有多少个 "s"。
h[i]:字符串 str 中 [0, i] 区间内有多少个 "sh"。
y[i]:字符串 str 中 [0, i] 区间内有多少个 "shy。
(2)状态转移方程
(3)空间优化
用三个变量来表示即可
s:(字符串 str 中 [0, n-1] 区间内有多少个 "s")
h:(字符串 str 中 [0, n-1] 区间内有多少个 "sh")
y:(字符串 str 中 [0, n-1] 区间内有多少个 "shy")
最后的遍历结束后,y即我们需要的结果
#include <iostream>
#include <string>
using namespace std;
typedef long long ll;
int main()
{int n;string str;cin >> n >> str;ll s = 0, h = 0, y = 0;for (int i = 0; i < n; i++) {if (str[i] == 's') s++;else if (str[i] == 'h') h += s;else if (str[i] == 'y') y += h;}cout << y << endl;return 0;
}🌈二维 dp
这道题目如果不是子序列,而是要求连续序列的,那就可以考虑用 KMP。
(1)dp[i][j] 含义
- string t="shy"
dp[i][j]:以 i-1 为结尾的 str 子序列中出现以 j-1 为结尾的 t 的个数为 dp[i][j]。
(2)递推关系
- str[i - 1] 与 t[j - 1]相等
- str[i - 1] 与 t[j - 1] 不相等
当 str[i - 1] 与 t[j - 1]相等时,dp[i][j] 可以有两部分组成:
- 一部分是用 str[i - 1] 来匹配,那么个数为 dp[i - 1][j - 1]。即不需要考虑当前 str 子串和 t 子串的最后一位字母,所以只需要 dp[i-1][j-1]。
- 一部分是不用 str[i - 1] 来匹配,个数为 dp[i - 1][j]。
为什么还要考虑不用 str[i - 1] 来匹配,都相同了指定要匹配?
🧩例如: str:shyy 和 t:shy ,str[3] 和 t[2] 是相同的,但是字符串 str 也可以不用 str[3] 来匹配,即用 str[0]str[1]str[2] 组成的 "shy"。当然也可以用 str[3] 来匹配,即:str[0]str[1]str[3] 组成的 "shy"。所以,当 str[i - 1] 与 t[j - 1] 相等时,dp[ i ][ j ] = dp[ i - 1 ][ j - 1 ] + dp[ i - 1 ][ j ];
当 str[i - 1] 与 t[j - 1] 不相等时,dp[i][j] 只有一部分组成,不用 str[i - 1] 来匹配(就是模拟在 str 中删除这个元素),即:dp[i - 1][j],所以递推公式为:dp[ i ][ j ] = dp[ i - 1 ][ j ];
为什么只考虑 “不用 str[i - 1] 来匹配” 这种情况, 不考虑 “不用 t[j - 1] 来匹配” 的情况呢?
🧩这里要明确,我们求的是 str 中有多少个 t,而不是求 t 中有多少个 str,所以只考虑 str 中删除元素的情况,即不用 str[i - 1] 来匹配 的情况。
(3)状态转移方程
dp[i][j]显然要从dp[i-1][?]递推而来。立即思考dp[i-1][j], dp[i-1][j-1]分别与dp[i][j]的关系。因为少一个字符,自然而然从当前字符着手。考察si的第i个字符(表为s[i])和tj的第j个字符(表为t[j])的关系。
若s[i] ≠ t[j]:那么s_i中的所有t_j子序列,必不包含s[i],即s_i-1和s_i中tj的数量是一样的,得到该情形的转移方程: dp[ i ][ j ] = dp[ i -1 ][ j ]
若s[i] = t[j]:假设s_i中的所有t_j子序列中,包含s[i]的有a个,不包含的有b个。s_i中包含s[i]的子序列个数相当于s_i-1中t_j-1的个数,不包含s[i]的子序列个数与上一种情况一样,于是得到该情形的转移方程:
a = dp[ i -1 ][ j -1 ] b = dp[ i-1 ][ j ] dp[ i ][ j ] = a + b = dp[i-1][j-1] + dp[i-1][j]
(4)遍历顺序
从上到下,从左到右。
#include <iostream>
#include <vector>using namespace std;int main()
{int n;cin >> n;string str;cin >> str;string t="shy";int m=t.size();vector<vector<long long>> dp(n+1, vector<long long>(m+1));for(int i=0; i<=n; i++) dp[i][0]=1;for(int i=1; i<=n; i++){for(int j=1; j<=m; j++){if(str[i-1]==t[j-1])dp[i][j]=dp[i-1][j-1]+dp[i-1][j];elsedp[i][j]=dp[i-1][j];}}cout << dp[n][m] << endl;return 0;
}2. 不同的子序列

该题于上题不一样的是,上面给定了t的具体字符串,而这里没有给定,但是我们也需要用二维dp的方法来写。
(1)dp[i][j] 含义
s[ i ]的子序列中在t[ j ]出现的次数
s[ i ]表示s从下标 i 到末尾的子字符串。
t[ j ]表示t从下标 j 到末尾的子字符串。
(2)递推关系
- 分别令两个维度为0,推测边界。
- dp[0][j]表示s_0中t_j的个数。s_0是空字符串,只有当j=0时,才有dp[0][j] = 1,表示s子空串中有一个t子空串,否则dp[0][j] = 0,因为一个空串不可能包含一个非空串。
dp[i][0]表示s_i中t0的个数。t_0是空字符串,显然任何串(包括空串)都含有一个空子串。因此dp[i][0] = 1。
注意到,dp[i][0] = 1实际上已经包含了dp[0][j] = 1的情形。
(3)初始化
- dp[i][0] 表示:以 i-1 为结尾的 str 可以随便删除元素,出现空字符串的个数。所以,dp[i][0] 一定都是 1,因为也就是把以 i-1 为结尾的 str,删除所有元素,出现空字符串的个数就是 1。
- dp[0][j] 表示:空字符串 str 可以随便删除元素,出现以 j-1 为结尾的字符串 t 的个数。所以,dp[0][j] 一定都是 0,因为 str 如论如何也变成不了 t。
- dp[0][0] 表示:空字符串 str 可以删除 0 个元素,变成空字符串 t。所以,dp[0][0] = 1。
(4)遍历顺序
从上到下,从左到右。
int numDistinct(string s, string t) {int n = s.size(), m = t.size();if (n < m) return 0;vector<vector<unsigned int>> dp(n + 1, vector<unsigned int>(m + 1)); //注意是unsigned intfor (int i = 0; i <= n; i++) dp[i][0] = 1;for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++) {dp[i][j] = dp[i - 1][j] +(s[i - 1] == t[j - 1] ? dp[i - 1][j - 1] : 0);}}return dp[n][m];
}相关文章:

【算法/训练】:动态规划(线性DP)
一、路径类 1. 字母收集 思路: 1、预处理 对输入的字符矩阵我们按照要求将其转换为数字分数,由于只能往下和往右走,因此走到(i,j)的位置要就是从(i - 1, j)往下走&#…...

计算巨头 Azure、AWS 和 GCP 的比较
云计算领域由三大主要参与者主导:Microsoft Azure、Amazon Web Services (AWS) 和 Google Cloud Platform (GCP)。每个平台都为希望利用云提供基础设施、平台服务等的企业提供强大的功能。在本文中,我们将深入探讨这些平台之间的差异,重点关注…...

Thinkphp5跨域问题常见的处理方法
在ThinkPHP5中,处理跨域问题通常涉及配置中间件或直接在控制器中设置响应头。以下是几种常见的解决跨域问题的方法: 1. 使用中间件处理跨域 你可以创建一个中间件来专门处理跨域请求。这个中间件会检查请求的来源,并设置相应的响应头来允许…...

Matlab编程资源库(9)数据插值与曲线拟合
一、一维数据插值 在MATLAB中,实现这些插值的函数是interp1,其调用格式为: Y1interp1(X,Y,X1,method) 函数根据X,Y的值,计算函数在X1处的值。X,Y是两个等长的已知向量,分别描述采样点和样本值,X1是一个向量…...

matplotlib的科研绘图辅助
matplotlib的科研绘图辅助 趁着暑假,与和鲸科技合作了一个python绘图的教程,作为暑期夏令营的一小部分,主要内容是介绍如何使用matplotlib、pandas、seaborn和plotnine进行医学科研绘图,感兴趣的可以通过如下地址进行访问&#x…...

C++内存管理(候捷)第五讲 笔记
GNU C对allocators的描述 new_allocator 和malloc_allocator,它们都没有特别的动作,无非底部调用operator new和malloc。它们没有用内存池 区别:::operator new是可重载的 智能型的allocator,使用内存池,分一大块然后…...

谷粒商城实战笔记-63-商品服务-API-品牌管理-OSS获取服务端签名
文章目录 一,创建第三方服务模块thrid-party1,创建一个名为gulimall-third-party的模块2,nacos上创建third-party命名空间,用来管理这个服务的所有配置3,配置pom文件4,配置文件5,单元测试6&…...

详细介绍BIO、NIO、IO多路复用(select、poll、epoll)
BIO、NIO、IO多路复用 BIO(Blocking IO)NIO(Non-blocking IO) 同步非阻塞IOIO多路复用selectpollepoll Redis的IO多路复用 BIO(Blocking IO) 最基础的IO模型,当进行IO操作时,线程会被阻塞,直到操作完成。 比如read和write,通常IO…...

昇思25天学习打卡营第11天|xiaoyushao
今天分享ResNet50迁移学习。 在实际应用场景中,由于训练数据集不足,所以很少有人会从头开始训练整个网络。普遍的做法是,在一个非常大的基础数据集上训练得到一个预训练模型,然后使用该模型来初始化网络的权重参数或作为固定特征提…...
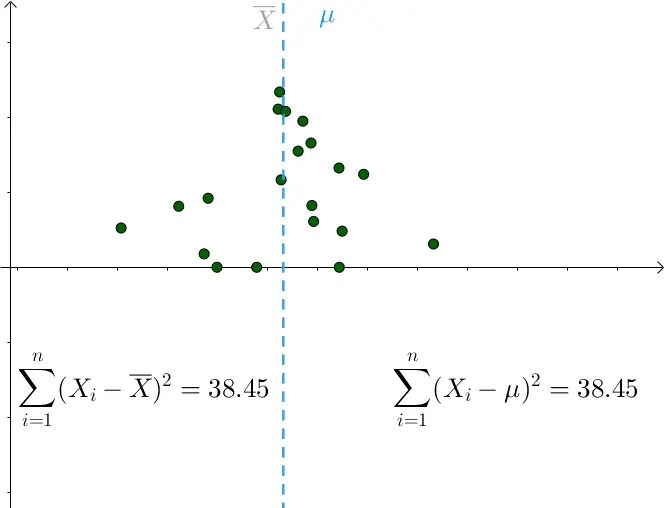
为什么样本方差(sample variance)的分母是 n-1?
样本均值与样本方差的定义 首先来看一下均值,方差,样本均值与样本方差的定义 总体均值的定义: μ 1 n ∑ i 1 n X i \mu\frac{1}{n}\sum_{i1}^{n} X_i μn1i1∑nXi 也就是将总体中所有的样本值加总除以个数,也可以叫做总…...

编解码器架构
一、定义 0、机器翻译是序列转换模型的一个核心问题, 其输入和输出都是长度可变的序列。 为了处理这种类型的输入和输出, 我们设计一个包含两个主要组件的架构: 第一个组件是一个编码器(encoder): 它接受一…...

追问试面试系列:JVM运行时数据区
hi 欢迎来到追问试面试系列之JVM运行时数据区,在面试中出现频率非常高,并且其中还存在一些误导性的面试,一定要注意。 什么误导性呢?面试中,有的面试官本来是想问JVM运行时数据区,不过提问时难免有些让你觉得很不爽。比如:你说说java内存模型,还比如说说JVM内存模型,…...

React Native在移动端落地实践
在移动互联网产品迅猛发展的今天,技术的不断创新使得企业越来越注重降低成本、提升效率。为了在有限的开发资源下迅速推出高质量、用户体验好的产品,以实现公司发展,业界催生了许多移动端跨平台解决方案。这些方案不仅简化了开发流程…...

《操作系统》(学习笔记)(王道)
一、计算机系统概述 1.1 操作系统的基本概念 1.1.1 操作系统的概念 1.1.2 操作系统的特征 1.1.3 操作系统的目标和功能 1.2 操作系统的发展与分类 1.2.1 手工操作阶段(此阶段无操作系统) 1.2.2 批处理阶段(操作系统开始出现࿰…...

LabVIEW学习-LabVIEW处理带分隔符的字符串从而获取数据
带分隔符的字符串很好处理,只需要使用"分隔符字符串至一维字符串数组"函数或者"一维字符串数组至分隔符字符串"函数就可以很轻松地处理带分隔符地字符串。 这两个函数所在的位置为: 函数选板->字符串->附加字符串函数->分…...

freesql简单使用操作mysql数据库
参考:freesql中文官网指南 | FreeSql 官方文档 这两天准备做一个测试程序,往一个系统的数据表插入一批模拟设备数据,然后还要模拟设备终端发送数据包,看看系统的承压能力。 因为系统使用的第三方框架中用到了freesql,…...

使用Java和Spring Retry实现重试机制
使用Java和Spring Retry实现重试机制 大家好,我是微赚淘客系统3.0的小编,是个冬天不穿秋裤,天冷也要风度的程序猿!今天,我们将探讨如何在Java中使用Spring Retry来实现重试机制。重试机制在处理临时性故障和提高系统稳…...
:自定义配置与插件管理)
Linux Vim教程(十):自定义配置与插件管理
目录 1. 概述 2. Vim 配置文件 2.1 .vimrc 文件 2.2 .gvimrc 文件 3. 自定义配置 3.1 自定义快捷键 3.2 自动命令 3.3 函数定义 4. 插件管理 4.1 插件管理工具 4.1.1 安装 vim-plug 4.1.2 配置 vim-plug 4.1.3 安装插件 4.2 常用插件 4.2.1 NERDTree 4.2.2 Fzf…...

代理协议解析:如何根据需求选择HTTP、HTTPS或SOCKS5?
代理IP协议是一种网络代理技术,可以实现隐藏客户端IP地址、加速网站访问、过滤网络内容、访问内网资源等功能。常用的IP代理协议主要有Socks5代理、HTTP代理、HTTPS代理这三种。代理IP协议主要用于分组交换计算机通信网络的互联系统中使用,只负责数据的路…...
Verilog语言和C语言的本质区别是什么?
在开始前刚好我有一些资料,是我根据网友给的问题精心整理了一份「C语言的资料从专业入门到高级教程」, 点个关注在评论区回复“888”之后私信回复“888”,全部无偿共享给大家!!! 用老石的一句话其实很好说…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...


