强化学习学习（三）收敛性证明与DDPG

证明收敛？

• 对于Value迭代：不动点证明的思路
  首先定义一个算子$\mathcal{B}:\mathcal{B}V={\max }_a{r}_a+\gamma {\mathcal{T}}_{a}V$
  接着有一个不动点$V^{\ast }(s)={\max }_{a}r(s,a)+\gamma E[V^{\ast }(s^{\prime })]$，有$V^{\ast }=\mathcal{B}{V}^{\ast }$
  每次使用算子都会，V离不动点的距离有收缩：$||\mathcal{B}V-V^{\ast }|{|}_{\infty }\le \gamma ||V-V^{\ast }|{|}_{\infty }$

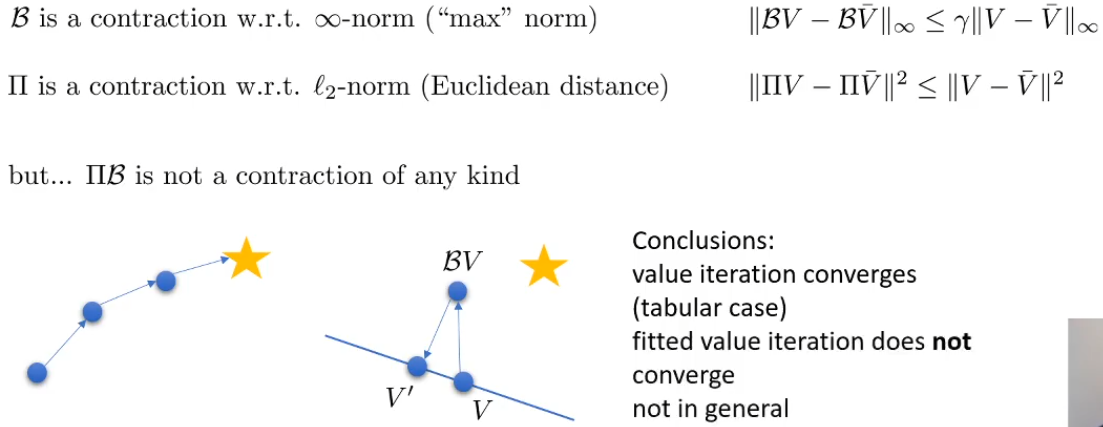
• 对于神经网络拟合的Value迭代：对于监督学习，也是得到一个$V^{\prime }$使得距离$||V^{\prime }(s)-(\mathcal{B}V)(s)|{|}^2$最小——投影
  V的迭代是这样的$V\leftarrow \Pi \mathcal{B}V$
  定义一个新的算子$\Pi :\Pi V=\arg {\max }_{V^{\prime }\in \Omega }\frac{1}{2}\sum ||V^{\prime }(s)-V(s)|{|}^2$，$\Pi$实际上是用l2范数对$\Omega$的投影，也是收缩的
  

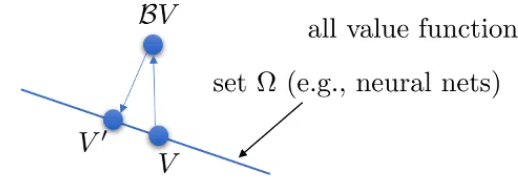
[!收缩：]
$||\Pi V-\Pi \bar{V}|{|}^2\le ||V-\bar{V}|{|}^2$(注意这里用的是2范数而上面是无穷范数，两种算子都是再各自的范数上收缩的)，但是把两个算子结合在一起就不会收缩了
所以就导致了使用Q-table能够保证收敛，而用神经网络拟合的V的Q-iteration不能够收敛

• 对于Q-iteration
  和上面一样，用神经网络拟合时不收敛，因为有投影算子
• 对于A-C
  也是再用神经网络拟合的时候不收敛

尽管理论上令人沮丧，但是实际中可以表现的很好！

Deep RL with Q-Functions

这里面包含了replay buffer和target network，但是暂时不细说了。
Polyak averaging：模型平均的问题

Double Q-Learning

在实际的使用过程中，Q-Learning总是出现overestimate的问题：估计的价值比实际的价值高很多：

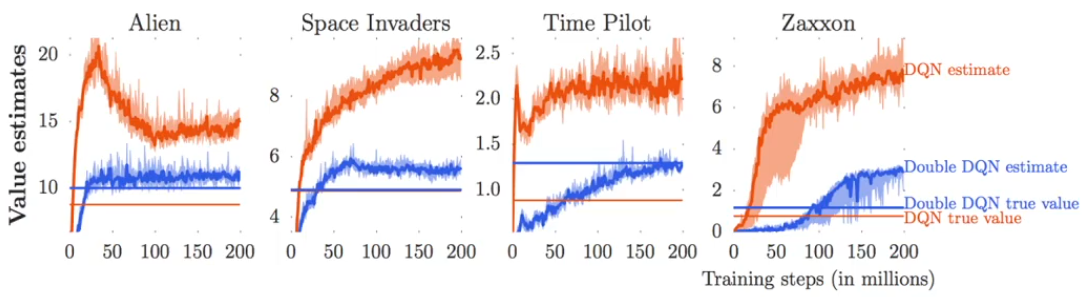
为什么会出现这样呢：
我们的target value是$y_i=r_i+\gamma {\max }_{a_j^{\prime }}{Q}_{{\varphi }^{\prime }}(s_j^{\prime },a_j^{\prime })$，其中${\varphi }^{\prime }$是当前的价值函数
imagine we have two random variables: $X_1,X_2$，We have $E[\max (X_1,X_2)]\ge \max (E[X_1],E{X}_2)$
而对于$Q_{{\varphi }^{\prime }}(s^{\prime },a^{\prime })$，它是对真正Q函数的估计，也就是真正的Q函数加上一些“噪声”，所以当我们取$Q_{{\varphi }^{\prime }}(s^{\prime },a^{\prime })$的最大值的时候，尽管“噪声”是无偏的，也会导致最后的值变大：
$$\underset{a^{\prime }}{\max }{Q}_{{\varphi }^{\prime }}(s^{\prime },a^{\prime })=Q_{{\varphi }^{\prime }}(s^{\prime },\arg \underset{a^{\prime }}{\max }{Q}_{{\varphi }^{\prime }}(s^{\prime },a^{\prime }))$$
为什么有上面这个式子的写法？ 别忘了遵循贪婪（没有”探索“）的策略，我们选择下一个action就是根据$Q_{{\varphi }^{\prime }}$的，因为是根据$\arg \max$选出来的，因此如果我们选择了正的噪声的action作为价值函数的输入，那么价值函数会基于同样的贪婪也会选择正的噪声，就会overestimate。

理论上的解法

因此，提出了Double Q-Learning，我们分别使用两个神经网络去产生动作和估计价值，这样两个神经网络拟合时产生的”噪声“就是不相关的！——这个操作非常像通信里面的啊！
$$Q_{{\varphi }_A}(s,a)=r+\gamma Q_{{\varphi }_B}(s^{\prime },\arg \underset{a^{\prime }}{\max }{Q}_{{\varphi }_A}(s^{\prime },a^{\prime }))$$
$$Q_{{\varphi }_B}(s,a)=r+\gamma Q_{{\varphi }_B}(s^{\prime },\arg \underset{a^{\prime }}{\max }{Q}_{{\varphi }_B}(s^{\prime },a^{\prime }))$$

实际上的解法

实际上，我们不需要麻烦的创造一个动作选择神经网络，一个价值神经网络，而是直接利用现成的：

别忘了我们其实有两个$\varphi$和${\varphi }^{\prime }$的，一个表示目标函数，另一个则是不断更新的，而目标函数会定期更新，因此我们直接借助这两个现成的：
$$y_i=r_i+\gamma Q_{{\varphi }^{\prime }}(s_j^{\prime },\arg \underset{a^{\prime }}{\max }{Q}_{\varphi }(s^{\prime },a^{\prime }))$$
上面利用当前的神经网络去确定动作action，而利用目标网络去确定价值value

DDPG: Q-Learning with continuous actions

• 各种对连续动作采样的方法
• DDPG

回忆一下，我们的目标是${\max }_a{Q}_{\varphi }(s,a)=Q_{\varphi }(s,\arg {\max }_a{Q}_{\varphi }(s,a))$
因此，想办法训练另一个网络${\mu }_{\theta }\approx \arg {\max }_a{Q}_{\varphi }(s,a)$，它可以看作是一个状态-动作函数，用来模拟$\arg \max$的过程
怎么去寻找这个网络的参数呢？因为我们是寻找最大的Q，因此用梯度上升就可以$\frac{d{Q}_{\varphi }}{d\theta }=\frac{da}{d\theta }\frac{d{Q}_{\varphi }}{da}$
新的target: $y_j=r_j+\gamma Q_{{\varphi }^{\prime }}(s_j^{\prime },{\mu }_{\theta }(s_j^{\prime }))\approx r_j+\gamma Q_{{\varphi }^{\prime }}(s_j^{\prime },\arg {\max }_{a^{\prime }}{Q}_{{\varphi }^{\prime }}(s_j^{\prime },a_j^{\prime }))$

Advanced tips for Q-Learning

• Q-Learning再不同问题上的稳定度很不同，因此需要首先确保稳定性，包括选择合适的随机数种子。
• 较大的replay buffer能够帮助提高稳定性
  • Looks more like fitted Q-iteration
• 学习可能需要很长时间才能有突破
• 进行探索的时候，先把$ϵ$设置大一点，随后慢慢的逐步减小
• Bellman error gradients can be big: clip gradients or use Huber loss instead$$L=\{\begin{array}{ll}{x}^2/2& \text{ if }|x|\le \delta \\ \delta |x|-{\delta }^2/2& \text{ otherwise }\end{array}$$
• 多使用Double Q-Learning，非常好用
• 变化的学习率或者Adam optimizer会很有帮助